| 基于CUDA架构的GF4影像快速正射纠正 |
2. 武汉大学计算机学院,湖北 武汉, 430072
2. School of Compute, Wuhan University, Wuhan 430072, China
GF4卫星是我国首颗地球同步轨道高分辨率光学成像卫星,也是目前世界上空间分辨率最高、幅宽最大的地球同步轨道遥感卫星,其搭载了一台可见光近红外50 m/中波红外400 m分辨率、幅宽约500 km/400 km的面阵相机[1],GF4卫星相机主要有可见光近红外通道和中波红外通道两个通道。
GF4卫星的可见光近红外通道单景影像数据量达到GB级,整轨数据量有上百GB,而随着高分四号卫星数据广泛应用于减灾、林业、地震、气象等领域,传统的串行处理架构和算法已无法满足在应急应用领域中对GF4影像的快速处理需求,以GPU为代表的高性能处理架构和并行算法已逐渐成为卫星数据处理的热点。正射纠正是GF4卫星数据应用于实际的关键处理环节,处理过程密集、耗时很长,而正射纠正的逐像素处理计算方法具有先天的并行性,非常适合于在GPU上并行处理[2]。
近年来,受交叉学科(如医学、物理学、地学等)对大数据问题快速求解的需求,基于GPU的高性能处理理论和方法研究进展迅速,遥感图像的快速处理研究也有所发展。在国际上,美国Intergraph公司推出了“像素管道”(Pixel Pipe),该系统也采用了各类先进的分布式并行计算技术大幅提高了正射影像图的生产效率[3];PCI Geomatics公司推出的GXL将摄影测量数据处理流程引入到开放式体系结构及标准化的硬件组件中,支持航空影像正射纠正流程[4]。在国内,侯毅等[5]使用GPU通用计算技术实现了遥感影像正射校正的并行处理,并对其效率和正确性进行了验证,说明了该技术的可行性;陈超等[6]研究了基于二维平面地形图的原始遥感影像几何校正方法,该方法仅进行了基本实现,未考虑性能优化,因此加速比较为有限。
如何通过算法设计把正射纠正算法各环节映射到GPU上处理,并结合GPU架构特点及并行编程模型特点对各并行环节进行性能优化,是实现基于GPU架构的快速正射纠正算法的关键。本文首先详细分析串行模式下正射纠正各环节并行性,然后系统地探讨基于GPU的快速正射纠正方法,以充分利用GPU架构的计算性能。
1 串行正射纠正算法 1.1 RPC模型精细化GF4卫星影像以有理多项式(rational polynomail cofficient,RPC)模型代替严格几何模型作为成像模型,RPC模型是一种能够获得与严格成像模型近似一致精度的、形式简单的通用拟合模型,在附加一定数量控制点情形下对RPC模型进行精化,可以获得很高的拟合精度[7-9]。大量学者对SPOT5、IKONOS、QuickBird等卫星影像进行了充分实验,证明由RPC模型可以得到高精度、高稳定性的结果[10-11]。此外,采用RPC模型可以隐藏卫星传感器的重要设计参数。因此光学遥感卫星大多采用RPC模型作为影像产品的成像模型。
RPC根据分母的阶数不同有9种不同的形式,当Dens(p, l, h)=Denl(p, l, h)=1时,RPC模型退化为一般三维多项式拟合模型,当Dens(p, l, h)=Denl(p, l, h)≠1并且NumL(p, l, h)和Nums(p, l, h)均为一阶多项式的情况下,RPC模型退化为直接线性变换(direct linear transformation, DLT)模型,因此RPC模型是一种广义的成像模型[7]。
为了得到高精度正射影像,本文先利用相应地区的参考影像(DOM)和参考地形数据(DEM)对RPC模型进行精细化,其具体流程如下:
1) 将GF4影像附加DEM与DOM进行控制点匹配,并人工删除误匹配点或调整不合理匹配点的位置,从而在GF4影像上得到大量分布均匀且可靠的控制点。本文中控制点匹配不是主要研究内容,控制点是使用开放式平台OpenRS来的控制点匹配功能得到的。
2) RPC模型所有的有理多项式系数作为待解参数,利用控制点的物方坐标和像方坐标对RPC拟合模型进行平差解算。
3) 将影像划分为均匀格网,在三维空间确定足够数量且具有一定高程间隔的高程面,通过原始RPC模型计算格网点对应各高程面上的物方坐标,即可得到足够数量检查点,如图 1所示[12]。将检查点物方坐标代入RPC模型中计算其像方坐标,通过计算原始影像格网点坐标与由RPC模型得到的坐标之差,对RPC模型拟合精度进行估计。
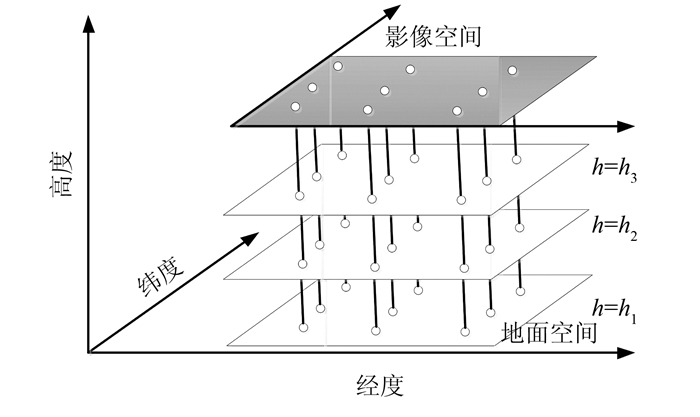 |
| 图 1 虚拟检查点格网示意图 Fig.1 Grids of Virtual Check Points |
1.2 基于RPC模型的正射纠正算法
光学卫星遥感影像的正射纠正是指按照一定数学模型,引入DEM参考地形数据共同消除原始影像中的各种畸变,获取一幅同区域的正射投影的新影像,其基本任务是实现两个二维图像间的几何变换[4]。目前常用的正射纠正方法包括直接法和间接法两种[13-14],直接法从原始影像计算到纠正结果影像,结果上容易没有灰度值的无效像元,而间接法从结果纠正影像计算到原始影像,灰度值通过重采样得到,不会出现无效像元,因此,本文采用以RPC模型为几何变换模型的间接纠正法,处理流程如下:
1) 由原始影像4个角点的影像坐标及DEM数据通过RPC模型正算到物方,结合正射影像的分辨率,计算影像尺寸,并构建正射结果影像。
2) 由结果影像上每个像元(l, s)计算相应地理坐标(Latitude, Longitude),根据地理坐标在参考DEM上内插出高程Height,由物方坐标(Latitude, Longitude, Height)及RPC模型映射到原始影像,得到相应像平面坐标(x, y)。
3) 在原始影像上内插出像点(x, y)的灰度,并赋值给当前的结果影像像元。
由以上流程可知,串行正射算法中RPC反算和灰度内插均需要逐像元进行,是最耗费时间的环节,针对此,本文提出了以下改进:
1) 映射到原始影像的像元灰度内插需要读取周围几个整数像元的灰度值,使得整体的读取操作过于频繁。改进方法是先在结果影像上选取一个区域范围,计算RPC反算到原始影像的像元区域,取这个区域的外包矩形,一次性读取到灰度数组中;
2) 映射到原始影像的像元取周围整数像元灰度值时都要判断整数像元坐标是否超出原始影像坐标边界,但同时使得影像内部大量非边界像元都进行了多余的分支判断。改进方法是在改进1)中取原始影像纠正区域范围的外包矩形时把矩形四至范围外扩5个像元,人为把边界点处理成非边界点;
3) 映射到原始影像范围内有可能出现无相应灰度值的像元,逐点取像元灰度时需要判断灰度值是否存在以免取灰度值出错,但同时大量灰度正常的像元进行了多余的分支判断。改进方法是把无灰度值的像元均赋值为灰度默认值,从而保证该像元在内插算法中不会影响到真实内插值。一般的灰度影像灰度默认值设为0,DEM影像的灰度默认值设为RPC模型中的高程起始值;
4) GF4影像的尺寸有将近一万多个像元,正射纠正的结果影像尺寸相应地也很大,一次性读取所有像元灰度到内存可能导致内存溢出。改进方法是对结果影像先进行格网划分,再按格网进行纠正,考虑到影像的灰度值存储是行优先方式,划分的每个格网列宽与结果影像列宽一致,格网高度则结合计算机内存中一次性可写入的内存上限设置合理数值。
2 快速正射纠正算法 2.1 CUDA架构原理GPU早期是用于图形计算加速的硬件设备,近年来基于GPU的通用计算技术发展迅速,而GPU硬件设计也愈加满足通用计算的需求[15]。目前常用的GPU通用计算的模型共有4种,其中NVIDIA公司提出的统一设备计算架构(compute unified device architecture,CUDA)在GPU通用计算领域最为流行。CUDA包括了NVIDIA对于GPU通用计算的完整解决方案:从GPU硬件架构的规范和设计,到对GPU数值计算的精度要求,以及编程接口和编译器的定义等,但CUDA只支持NVIDIA公司生产的GPU显卡设备[16]。图 2展示了CUDA基本编程模型:CPU负责处理串行任务和流程控制;GPU负责处理并行任务,具体方式是将需要并行处理的逻辑组织为核函数,当核函数执行时,GPU硬件会产生大量线程,并将所有线程组织成线程格网和线程块,分别对相应数据进行处理[17],核函数是CUDA程序中并行思想的集中体现,快速正射纠正算法将针对正射纠正串行算法特点设计相应核函数。
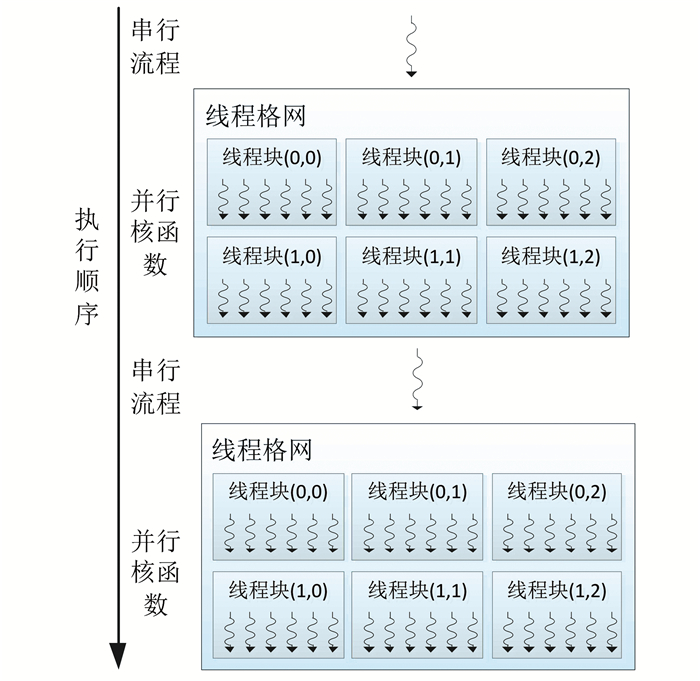 |
| 图 2 CUDA编程模型 Fig.2 Programming Model of CUDA |
2.2 正射纠正并行算法
正射纠正串行处理流程中RPC反算和灰度内插环节对于结果影像的每个像元都相互独立,不存在逻辑冲突,非常适合于数据并行模式,此外,这两个环节在整个处理流程中计算量最大、耗时最多,有必要并行化,而其他环节计算量小、执行次数少,考虑到并行化带来的数据IO时间消耗,不宜对其并行化。因此仅将RPC反算和灰度内插映射到并行化核函数。由于硬件限制,GPU将线程组织成线程块和线程格网的层次形式,相应地,并行算法中将采用层次性分块的策略分配计算数据到线程。具体做法是先按照影像分块策略给结果影像分块,纠正某块结果影像时,将整块结果影像作为底层块,与GPU线程格网对应;再将整块结果影像进行逻辑切割,形成二层逻辑块,使得每一个每个二层逻辑块与一个GPU线程块对应,且尺寸与GPU线程块尺寸保持一致,以保证每个线程都对每一个像素进行处理[2]。
本文结合RPC精细化过程及串行处理环节优化策略,设计基于CUDA架构的快速正射纠正算法如图 3所示。
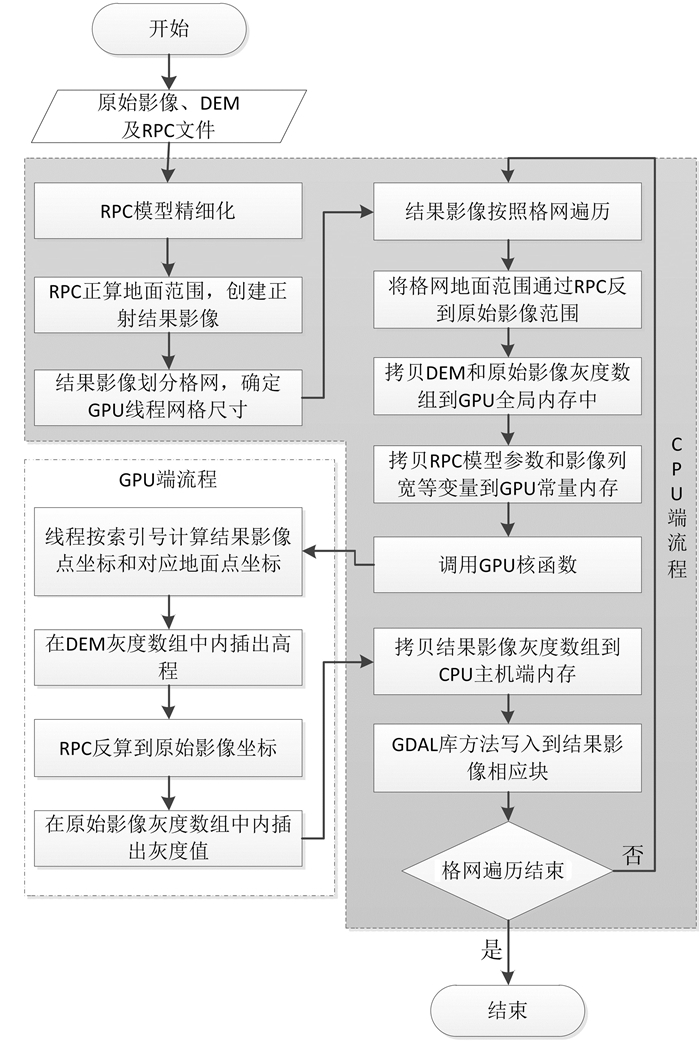 |
| 图 3 基于CUDA架构的快速正射纠正算法 Fig.3 Quick Orthographic Rectification Algorithm Based on CUDA |
3 实验分析
本文以GF4的PMS影像作为实验数据,实验环境中CPU型号为Intel Xeon E5-2430,含6个计算核心,主频2.50GHZ;GPU为主流的Kepler架构NVIDIA Quadro K2000,含384个计算核心,全局内存大小2 GB,常数存储器和GPU片上缓存都为64 KB,峰值浮点计算性能为384 Gflops;主机内存大小为48 GB。
在该实验环境下,本文首先对串行算法中除RPC精细化外主要环节的时间消耗进行了对比分析(其中内插环节都采用双线性内插法),表 1列出了5景GF4的PMS影像的实验结果。从表 1中可知,串行正射纠正流程中内插和RPC反算所需时间较长,是进行并行改进的主要环节。
| 表 1 串行算法各环节所需时间 Tab.1 Calculation Time of Each Process in the Serial Algorithm |
 |
本文使用时间加速比对于效率性能进行评价,定义如下[16]:
| $ {S_p} = \frac{{{T_s}}}{{{T_p}}} = \frac{{{W_s} + {W_p}}}{{{W_s} + \frac{{{W_p}}}{n}}} $ |
式中,Ts为串行正射纠正算法所需时间; Tp为并行改进的正射纠正算法所需时间; Sp为加速比; Ws为并行算法中的串行分量; Wp为并行算法中的并行分量,n为并行处理器数量。
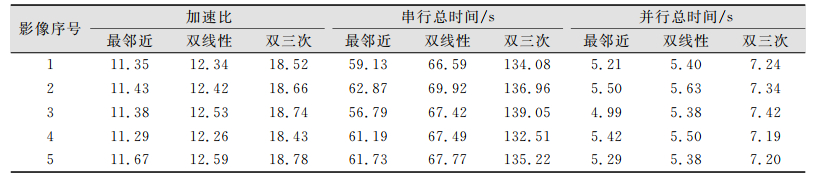
可以看出,在并行硬件设备一定的情况下,通过并行算法设计增加并行分量,可以提高最终的算法加速比,但必须权衡算法整体时间复杂度以保证最终的效率足够高。本文中,正射纠正的内插过程耗时最多,而内插算法一般分为最邻近法、双线性内插法、双三次内插法3种,其中双三次内插法算法运行时间复杂度最高,当采用这种内插方法时,并行化后并行分量比例相对其他两种较高,但总体时间消耗较多,以表 1中的GF4数据对3种方法分别统计其加速比和运行总时间,结果如表 2所示。从表 2中可以看出,最邻近法运行时间相对来说提高不多但精度没有其他两种方法高,而双三次内插法加速比高但运行时间相对过长,综合来看,采用双线性内插法最为合适。
| 表 2 3种内插方法加速比及总体时间 Tab.2 Speedup Ratio and Whole Calculation Time of Three Interpolating Algorithms |
 |
ENVI软件作为遥感影像处理领域成熟的商业软件,其正射纠正的效率经过充分优化,且正射的结果影像可视为准确无误。为了验证上述快速正射纠正算法的正确性和性能,本文算法与ENVI软件的正射纠正做对比,对GF4的PMS影像进行了4组实验:
1) 并行算法与串行算法结果对比效率,以验证并行算法理论上的性能优化程度;
2) 与该地区已有正射影像DOM匹配,以验证并行算法获取的影像几何精度;
3) 与ENVI纠正的结果影像进行差值计算,统计差值影像中非零像元比例,以验证正射纠正算法的准确性;
4) 与ENVI正射纠正流程对比效率,以验证并行算法实际应用的性能优化程度。
以影像GF4_PMS_E105.4_N40.0_20170106_L1A0000153805为实验对象,进行上述3组队比实验,结果如下:
1) 采用双线性内插法的并行改进算法相对于串行算法加速比为12.34,加速效果显著;
2) 与参考影像DOM匹配中误差为0.2个像素,匹配点最大残差不超过0.5个像素,说明并行算法结果几何精度较高;
3) 与ENVI纠正影像的差值影像中非零像元比例为0.03%,说明并行算法准确性较高;
4) 与ENVI正射纠正流程对比效率,在上述实验环境下,ENVI纠正该景影像时间为8 s左右,而并行算法耗时为7.4 s,说明并行算法实际应用性能较好,考虑到GPU硬件本身性能,该算法的实际应用性能应结合实际硬件条件进行评价。
通过以上分析可知,本文所述的正射纠正的并行改进算法获取的影像与ENVI获取的正射影像几乎相同,说明了本文算法的正确性。此外,由于算法最开始对GF4影像的RPC模型进行了精化处理,得到精度较高的RPC模型,与同类算法相比,本文算法可以保证纠正后的影像具有较高的几何精度。
4 结束语GF4影像应用领域广泛,其正射影像是应用实际的重要产品,正射影像的快速准确处理是解决实际应用中处理效率瓶颈的必要手段。本文系统地分析了串行正射纠正算法各环节的并行性,然后结合CUDA编程思想,提出了快速正射纠正算法。经过实验对比验证,该算法结果准确,速度提升了12倍多,有一定的应用价值。
| [1] |
吴月辉, 蒋建科.高分四号, 世界上空间分辨率最高、幅宽最大的地球同步轨道遥感卫星[N].人民日报, 2015-12-30(12)
|
| [2] |
方留杨, 王密, 李德仁. CPU和GPU协同处理的光学卫星遥感影像正射纠正方法[J]. 测绘学报, 2013, 42(5): 668-675. |
| [3] |
曹天景, 万幼川, 陈军, 等.先进测绘技术服务数字城市建设[EB/OL]. [2014-04-18]. http://www.d3dweb.com/Documents/201404/18-14324174367.html
|
| [4] |
杨靖宇.摄影测量数据GPU并行处理若干关键技术研究[D].郑州: 信息工程大学, 2011 http://cdmd.cnki.com.cn/Article/CDMD-90008-1012324989.htm
|
| [5] |
侯毅, 沈彦男, 王睿索, 等. 基于GPU的数字影像的正射纠正技术的研究[J]. 现代测绘, 2009, 32(3): 10-11. DOI:10.3969/j.issn.1672-4097.2009.03.003 |
| [6] |
陈超, 陈彬, 孟剑萍. 基于GPU大规模遥感图像的几何校正[J]. 指挥信息系统与技术, 2012, 3(1): 76-80. DOI:10.3969/j.issn.1674-909X.2012.01.018 |
| [7] |
张过, 李德仁. 卫星遥感影像RPC参数求解算法研究[J]. 中国图象图形学报, 2007, 12(12): 2080-2088. |
| [8] |
祝小勇, 张过, 秦绪文. 国产光学卫星影像RPC制作[J]. 国土资源遥感, 2011, 21(2): 32-34. |
| [9] |
张过, 厉芳婷, 江万寿, 等. 推扫式光学卫星影像系统几何校正产品的3维几何模型及定向算法研究[J]. 测绘学报, 2010, 39(1): 34-38. |
| [10] |
González C, Resano J, Mozos D, et al. FPGA Implementation of the Pixel Purity Index Algorithm for Remotely Sensed Hyperspectral Image Analysis[J]. Eurasip Journal on Advances in Signal Processing, 2010(1): 1-13. |
| [11] |
Fraser S, Ravanbakhsh M. Georeferencing Accuracy of GeoEye-1 Imagery[J]. Photogrammetric Engineering and Remote Sensing, 2009, 75(6): 634-638. |
| [12] |
Tao C V, Hu Y. A Comprehensive Study on the Rational Function Model for Photogrammetric Processing[J]. Photogrammetric Engineering and Remote Sensing, 2001, 67(12): 1347-1357. |
| [13] |
李德仁, 王树根, 周月琴. 摄影测量与遥感概论[M]. 第2版. 北京: 测绘出版社, 2008.
|
| [14] |
Kirk D, Hwu W M. Programming Massively Parallel Processors[M]. 2nd ed. Massachusetts: Morgan Kaufmann Publishers, 2012.
|
| [15] |
刘鹏, 何雯, 肖巍巍. 基于GPGPU技术快速提取数字表面模型[J]. 测绘地理信息, 2014, 39(2): 81-84. |
| [16] |
张舒, 褚艳利. GPU高性能计算之CUDA[M]. 北京: 中国水利水电出版社, 2009.
|
| [17] |
李朋龙, 邓非, 何江, 等. GPU-CPU协同航空影像快速正射纠正方法[J]. 测绘地理信息, 2016, 41(2): 44-47. |
 2019, Vol. 44
2019, Vol. 44

