灰色预测模型(gray model, GM)是邓聚龙于20世纪80年代提出的^[1]。由于该模型并不需要大量的原始数据就可以较好地拟合并预测的优点^[2]，广泛应用于各个科学领域，并取得了良好的效果。GM(1，1)模型是其核心内容，但模型具有一定的局限性。相关研究认为，GM(1，1)模型对于呈指数变化的数据具有较高的拟合与预测精度。但随着研究的不断深入，发现事实并非如此。例如文献[3]的算例中，虽然其原始数据近似地符合指数增长，但是用GM(1，1)模型拟合得到的结果却并不理想。研究发现，真正影响GM(1，1)模型拟合精度的是原始数据的光滑度。许多学者针对GM(1，1)模型精度改进进行了一系列的数据处理，如傅里叶残差修正^[4]、对数函数变换^[3]、一次函数变换^[5]、n次开方变换^[6]和cotx变换^[7]等，在一定程度上提高了模型精度。

本文在以上研究的基础上，提出了一种新的$\frac{{{x_k}}}{{{k^\alpha }}}\left({\alpha > 0} \right)$变换方法，提高了原始数据的光滑度，并从理论上证明了该方法的可行性，利用实验数据将计算结果与原始GM(1，1)模型和其他的改进方法进行了比较，取得了良好的效果。

1 $\frac{{{x_k}}}{{{k^\alpha }}}$变换的特征分析 1.1 光滑性比较原则

光谱性比较原则最早由邓聚龙提出^[1]。提高原始数据的光滑性已是被大众接受的一种提高灰预测建模精度的方法^[8]。

引理:设有非负序列X=(x(1), x(2), …, x(n)), Y=(y(1), y(2), …, y(n)), 若有$\frac{{y\left(k \right)}}{{\sum\limits_{i = 1}^{k - 1} {y\left(i \right)} }} \le \frac{{x\left(k \right)}}{{\sum\limits_{i = 1}^{k - 1} {x(i)} }}$，其中, k=2, 3, …, n，则称Y序列比X序列更光滑^[9]。

下面证明本文提出的$\frac{{{x_k}}}{{{k^\alpha }}}\left({\alpha > 0} \right)$的变换方法可以提高原始数据的光滑度。

证明：由于x_k非负，1/k^α非负且单调递减，那么对于i=1, 2, …, k-1，有：

$ {x_k} \times \frac{1}{{{k^\alpha }}} \times {x_i} < {x_k} \times \frac{1}{{{i^\alpha }}} \times {x_i} $

(1)

对两边求和得到:

$ \frac{{{x_k}}}{{{k^\alpha }}}\sum\limits_{i = 1}^{k - 1} {{x_i}} < {x_k} \times \sum\limits_{i = 1}^{k - 1} {\frac{{{x_i}}}{{{i^\alpha }}}} $

(2)

从而，有：

$ \frac{{\frac{{{x_k}}}{{{k^\alpha }}}}}{{\sum\limits_{i = 1}^{k - 1} {\frac{{{x_i}}}{{{i^\alpha }}}} }} < \frac{{{x_k}}}{{\sum\limits_{i = 1}^{k - 1} {{x_i}} }} $

(3)

所以变换$\frac{{{x_k}}}{{{k^\alpha }}}\left({\alpha > 0} \right)$提高了原始序列的光滑度。

证毕。

1.2 变换还原不扩大相对误差

使用变换还原不扩大相对误差方法处理的数据，其逆变换的相对误差不会增大。所以参数α的选择范围更大，利于编程不断拟合出最佳参数。

证明：令${y_i} = \frac{{{x_i}}}{{{i^\alpha }}}$，δ为GM(1，1)模型的原始误差，变换后为：

$ {z_i} = {y_i}\left( {1 - \delta } \right) $

(4)

逆变换后为：

$ x = {z_i} \times \left( {1 - \delta } \right) \times {i^\alpha } = {x_i} \times \left( {1 - \delta } \right) $

(5)

证毕。

同样，对文献[3]和文献[5]的变换方法作相应的分析，文献[3]的lnx变换法进行逆变换后为：

$ X = x_i^{\left( {1 - \delta } \right)} $

(6)

变换误差会随着原始数据x_i的增大而呈指数增长。文献[5]的ax+b变换法进行逆变换后为：

$ X = \left( {1 - \delta } \right){x_i} - \frac{b}{a}\delta $

(7)

因其要求a < 0, 所以其逆变换后的相对误差会变大，不过相比文献[3]中的逆变换误差，文献[5]的较为稳定，且为一个恒量，不会出现原始数据过大而逆变换误差大的情况。

2 基于$\frac{{{x_k}}}{{{k^\alpha }}}\left({\alpha > 0} \right)$变换的GM(1, 1)模型

基于$\frac{{{x_k}}}{{{k^\alpha }}}\left({\alpha > 0} \right)$变换的GM(1, 1)模型建模过程如下：

1) 原始序列为：

$ {Y^{\left( 0 \right)}} = \left\{ {\left. {{y^{\left( 0 \right)}}\left( 1 \right),{y^{\left( 0 \right)}}\left( 2 \right), \cdot \cdot \cdot ,{y^{\left( 0 \right)}}\left( n \right)} \right\}} \right. $

(8)

式中, Y⁽⁰⁾为非负序列，且i=1, 2, …, n。

2) 对原始数据进行基于$\frac{{{x_k}}}{{{k^\alpha }}}\left({\alpha > 0} \right)$变换的处理：

$ {X^{\left( 0 \right)}} = \left\{ {\left. {{x^{\left( 0 \right)}}\left( 1 \right),{x^{\left( 0 \right)}}\left( 2 \right), \cdot \cdot \cdot ,{x^{\left( 0 \right)}}\left( n \right)} \right\}} \right. $

(9)

式中, X⁽⁰⁾(k)=Y⁽⁰⁾(k)/k^α(α>0)，k=1, 2, …, n。

3) 进行一次累加^[10]，则有：

$ {X^{\left( 1 \right)}} = \left\{ {\left. {{x^{\left( 1 \right)}}\left( 1 \right),{x^{\left( 1 \right)}}\left( 2 \right), \cdot \cdot \cdot, {x^{\left( 1 \right)}}\left( n \right)} \right\}} \right. $

(10)

式中, ${x^{(1)}}\left(k \right) = \sum\limits_{i = 1}^k {{x^{(0)}}\left(i \right)} {\rm{ }}$，k=1, 2, …, n。

4) 建立X⁽¹⁾的一阶微分方程为：

$ \frac{{{\rm{d}}{X^{\left( 1 \right)}}}}{{{\rm{d}}t}} + a{X^{\left( 1 \right)}} = u $

(11)

式中, a和u为模型待估参数，记为${\mathit{\hat a}}$ =[a, u]。

5)求解待估参数${\mathit{\hat a}}$：

$ \widehat a = {\left( {{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{B}}} \right)^{ - 1}}{\mathit{\boldsymbol{B}}^{\rm{T}}}{\mathit{\boldsymbol{Y}}_N} $

(12)

式中，

$ \mathit{\boldsymbol{B = }}\left[ {\begin{array}{*{20}{l}} { - {Z^{\left( 1 \right)}}\left( 2 \right)}&1\\ { - {Z^{\left( 1 \right)}}\left( 3 \right)}&1\\ {\;\;\;\;\; \vdots }& \vdots \\ { - {Z^{\left( 1 \right)}}\left( n \right)}&1 \end{array}} \right];{\mathit{\boldsymbol{Y}}_N} = \left[ {\begin{array}{*{20}{l}} {{x^{\left( 0 \right)}}\left( 2 \right)}\\ {{x^{\left( 0 \right)}}\left( 3 \right)}\\ {\;\;\;\; \vdots }\\ {{x^{\left( 0 \right)}}\left( n \right)} \end{array}} \right]; $

$ {Z^{\left( 1 \right)}}\left( k \right) = \frac{1}{2}\left[ {{x^{\left( 1 \right)}}\left( k \right) + {x^{\left( 1 \right)}}\left( {k - 1} \right)} \right]。$

6) 求解原始数据。求得${\mathit{\hat a}}$带入式(11)得到微分方程：

$ {\widehat x^{\left( 1 \right)}}\left( {k + 1} \right) = \left( {{x^{\left( 0 \right)}}\left( 1 \right) - \frac{u}{a}} \right){{\rm{e}}^{ - ak}} + \frac{u}{a} $

(13)

对${{\hat x}^{(1)}}$累减生成:

$ {\widehat x^{\left( 0 \right)}}\left( k \right) = {\widehat x^{\left( 1 \right)}}\left( k \right) - {\widehat x^{\left( 1 \right)}}\left( {k - 1} \right) $

(14)

逆变换得到原始序列为：

$ {\widehat y^{\left( 0 \right)}}\left( k \right) = {\widehat x^{\left( 0 \right)}}\left( k \right) \times {k^\alpha } $

(15)

式中，k=1, 2, …, n时, ${{\hat y}^{(0)}}$(k)为拟合值；k>n时, ${{\hat y}^{(0)}}$(k)为预测值。

根据平均相对误差最小的原则，通过MATLAB程序可以确定α的大小。根据大量数据实验得出，最佳α值一般介于0~5。因此，为了提高数据处理速度，本文建议以0.1为起始值，0.01为间隔，范围定为0.1~5。

3 实例分析

本文采用某大型钢铁联合企业一号高炉的沉降数据^[11](取前10期数据进行模拟；对后两期进行预测，并用*标注)进行建模预测。本例中，α=0.81，改进后模型的后验差比值C=S₂/S₁=0.064 8，其中，原始数列x⁽⁰⁾的方差S₁²=618.427 6, 残差数列e的方差S₂²=2.622 3，小误差概率$p = \left\{ {p\left| {e\left(i \right) - \bar e} \right| < 0.674\; 5\; {S_1}} \right\} = 1$，传统GM(1, 1)模型的后验差比值为C=0.244 1。

笔者将本文建模结果与传统GM(1，1)、文献[3]中的lnx变换、文献[5]中ax+b变换的方法进行了对比，4种建模方法的精度如表 1所示。

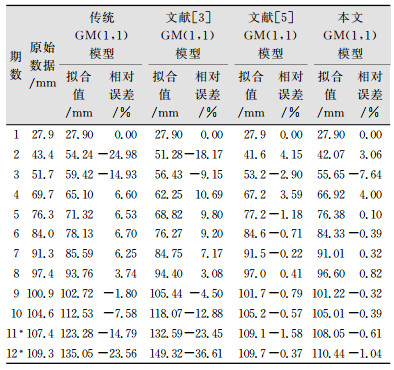从表 1可以看出，本文的x_k/k^α方法对于传统GM(1，1)模型精度有较大的提高，且效果好于文献[3]的lnx变换方法，与文献[5]的方法效果基本相同。不过文献[5]的一次变换法ax+b有两个参数a、b，而本文x_k/k^α只有一个参数α，计算简便且便于编写程序。

众所周知，GM(1, 1)的优势是可以只根据很少的数据进行建模，即在贫信息的前提条件下去探寻这些数据的规律。而本文的x_k/k^α数据变换方法可以扩大这种优势。以本文数据为例，10期数据中取1、3、5、7、9期数据对11期数据进行预测, 预测结果为104.10 mm，相对误差为3.07%；10期数据中取1、4、7期数据对11期数据进行预测，预测结果为103.73，相对误差为3.42%。显然预测的相对误差会随着数据量的减少而增大，不过本例经过x_k/k^α变换后，只用3期数据的相对误差仍然小于传统GM(1, 1)模型利用10期数据所得到的相对误差。

另外，再以三峡某危岩体变形监测点5月的监测资料^[11]为例，用本文x_k/k^α变换法与传统的GM(1, 1)模型进行对比(取前6期数据进行模拟，后两期进行预测，对其进行*标注)，如表 2所示。

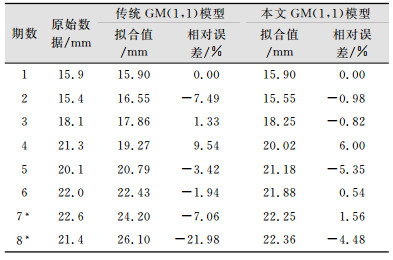本例中，α=0.57，其中，原始数列x⁽⁰⁾的方差S₁²= 6.44；本文模型残差数列e的方差S₂²=0.474 8，后验差比值C=S₂/S₁=0.271 5；传统模型下残差数列e的方差S₂²=1.028 9，后验差比值C=S₂/S₁=0.399 7。可见，本文方法有效地提高了模型精度。再从7、8两期的数据预测结果来看，传统模型已经将原本的平稳趋势误解读为上升趋势，而本文方法处理后的数据趋势与原始观测数据基本一致。

4 结束语

本文从提升原始数据光滑度的角度出发，提出了x_k/k^α(α>0)变换，用严格的数学公式推理论证了该变换的有效性，并通过实例验证了该方法的可行性，提高了传统GM(1, 1)的拟合精度与预测精度，拓宽了灰预测模型的应用范围。