| 引大济岷工程分段抵偿投影面和投影带的合理选择 |
根据《水利水电工程测量规范》SL197⁃2013,在大、中型工程测量中,控制网平面坐标系统应采用现行国家2000坐标系统,或与其相联系的独立坐标系统,主要目的是确保测量资源不浪费。国家2000坐标系统采用高斯⁃克吕格正形投影(简称高斯投影),即先由高程面投影到参考椭球面,再由参考椭球面投影到高斯平面,而高程面则投影到大地水准面上。高斯投影将中央经线投影为直线,其长度没有变形,与球面实际长度相等,其余经线为向极点收敛的弧线,距中央经线愈远,变形愈大。而规范规定[1],测区长度投影变形值不大于5 cm/km(即相对误差为1/20 000)。对于东西走向、高差大的工程,国内外文献介绍得比较少,由于本工程处于水系发达的四川,工程投影只采用单一的抵偿高程面或移动中央子午线都无法使长度投影变形满足规范要求,为了本工程控制网的边长变形能满足大比例地形图的施测,当边长的综合变形较大而不能满足相应要求时,可采用抵偿高程面和移动中央子午线的方法来改善测区内边长经投影后的综合变形[2, 3]。根据工程的特点和要求,建立测区的独立坐标系,而独立坐标系的建立,关键在于合理地选择投影带和投影面。由于引大济岷工程线路比较长,东西走向高差大,所以需采取分段投影方式进行平差计算[4]。
1 引大济岷工程抵偿投影面和投影带 1.1 工程概况引大济岷工程指四川省引调大渡河、青衣江水至岷江流域,解决成都天府新区水资源短缺的特大型跨区域调水工程。大渡河泸定电站为取水口,途径青衣江引入岷江成都段。引大济岷工程长达200 km,途经山区,再到成都平原,高程由1 500 m降至成都平原500 m左右,高程差达到1 000 m。为了解决任意带高斯正形投影和高程面投影到参考椭球面的变形,从平原区向山区(乃至高原地区)延伸,测区高程面由500 m增加到1 500 m,由于高程面的不同所产生的长度变形对引大济岷工程的影响是必须解决的问题。
1.2 引大济岷工程国家1∶10 000地形图换带的确定中国版图的经度范围约为东经73º30'~135º03',可分成11个6º带或22个3º带,6º带可用于中小比例尺(1∶25 000以下)测图,3º带可用于大比例尺(如1∶10 000)测图[5]。分带图如图 1所示。
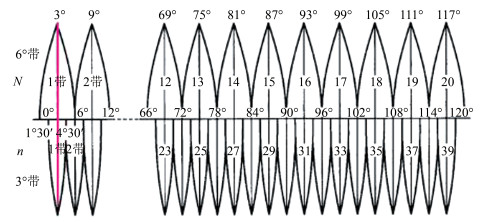 |
| 图 1 分带划分图 Fig.1 Zone Division Diagram |
换带原因:为了限制高斯投影的长度变形,以中央子午线进行分带,把投影范围限制在中央子午线东、西两侧一定的范围内,使得统一的坐标系分割成独立带的坐标系。在工程应用中,往往要用到相邻带中的控制点坐标,工程测量中要求采用6º带、3º带或任意带,因为国家控制点通常只有6º带坐标,需要时要将6º带坐标转换为3º带坐标。高斯投影的特点:离中央子午线愈远,长度变形愈大[6, 7]。如图 2所示。
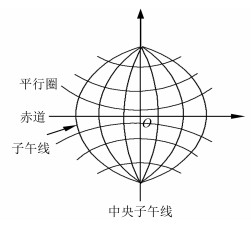 |
| 图 2 高斯投影 Fig.2 Gauss Projection |
引大济岷工程的地理位置范围为北纬29º56'~ 30º47'、东经102º12'~104º09'。在国家1∶10 000地形图中共跨两个投影带:102º带和105º带。引大济岷工程是一个整体,必须对国家1∶10 000地形图进行换带,为了减小高斯投影变形对地形图的影响,应对102º带和105º带投影变形对地形图影响的大小进行确认。
引大济岷工程共布设三等GPS平面控制点34个点(编号为
如图 3所示,实测边长水平距离归化到测区参考椭球面上的改正数为[8]:
| $ \delta_{H}=-H S_{H} /\left(R_{H}+H\right) $ | (1) |
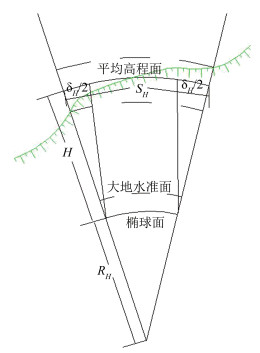 |
| 图 3 边长归化 Fig.3 Side Length Normalization |
式中,RH为测区所在椭球曲率半径(取6 368 km);H为长度所在高程面对于椭球面的高差;SH为实地测量的长度平距。
参考椭球面上的长度投影至高斯平面的改正数为[9]:
| $ \delta_{L}=S Y_{m}^{2} / 2 R^{2} $ | (2) |
式中,Ym为边长两端离测区中央子午线的横坐标差(以测段起点为原点);S为高斯平面上的边长(取S≈SH);R为测区所在参考椭球曲率半径(取R =6 368 km)。
可得长度综合变形为:
| $ \delta=\delta_{H}+\delta_{L}=S Y_{m}^{2} / 2 R^{2}-H S_{H} /\left(R_{H}+H\right) $ | (3) |
| $ \delta / S=\left|Y_{m}^{2} / 2 R^{2}-H /\left(R_{H}+H\right)\right| \leqslant 1 / 20000 $ | (4) |
H(m)与Y(km)关系如图 4所示。图 4中适应区表示长度综合变形能满足规范要求,不适应区表示长度综合变形不能满足规范要求。
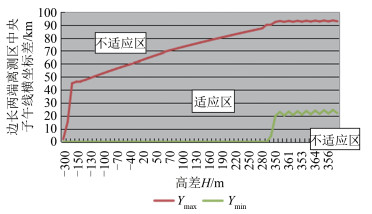 |
| 图 4 综合变形适应图 Fig.4 Comprehensive Deformation Adaptation Diagram |
2 分段投影抵偿高程面及中央子午线的选择
引大济岷工程平均高程面为800 m左右,须求取抵偿高程面和中央子午线的适用范围,以满足测区长度投影变形值不大于5 cm/km(即相对误差为1/20 000)的规范要求。在确定引大济岷工程高程抵偿投影面的过程中,为了使高程抵偿投影面尽量接近测区工程面,根据GPS控制坐标分布,如图 5所示,东西走向,高差起伏较大,为了使高程抵偿投影面尽量接近测区工程面,通过测区高差和两端离测区中央子午线横坐标差分析确定分为3段投影,如果分段投影过多,会导致施工过程中对不同带的坐标进行频繁转换,不方便施工,利用抵偿投影高程面和移动中央子午线来抵偿两项改正变形,即为高程抵偿面的任意带高斯正形投影[10, 11]。
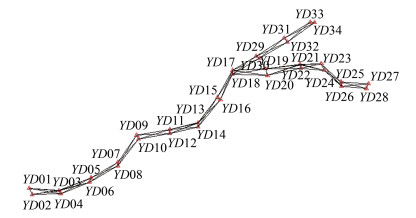 |
| 图 5 GPS控制网图 Fig.5 GPS Control Network Diagram |
2.1 根据分段测区平均高程确定抵偿投影高程面
抵偿投影高程面的选择分为以下几段,如表 1所示。
| 表 1 引大济岷工程分段抵偿投影高程面分段表 Tab.1 The Segmentation of Yindajimin Project Offsets the Projection Elevation Face Segment Table |
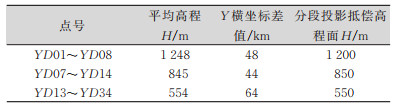 |
1)YD01~YD08:平均高程为1 248 m,抵偿投影高程面取值测区平均高程附近值1 200 m,则高程面投影变形系数为:
| $ \begin{aligned} &\beta=-H_{\Delta} / R_{H} \\ &\beta_{\text {最高点}}=-(1507.7-1200) / 6368000=-1 / 20695 \\ &\beta_{\text {最低点}}=-(978-1200) / 6368000=1 / 28684 \end{aligned} $ |
由此可知所取高程面投影变形系数绝对值都小于1/20 000,说明YD01~YD08高程抵偿面的选择合理。
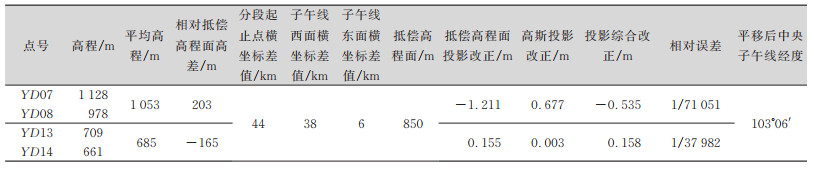
2)YD07~YD14:平均高程为844 m,抵偿投影高程面取值测区平均高程附近值850 m,则高程面投影变形系数为:
| $ \begin{aligned} &\beta=-H_{\Delta} / R_{H}\\ &\beta_{\text {最高点 }}=-(1127-850) / 6368000=-1 / 22989\\ &\beta_{\text {最低点 }}=-(661-850) / 6368000=1 / 33693 \end{aligned} $ |
同理可知所取高程面投影变形系数绝对值都小于1/20 000,说明YD07~YD14高程抵偿面的选择合理。
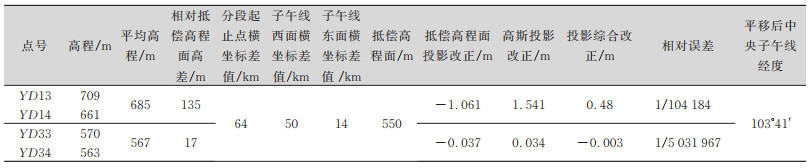
3)YD13~YD34:平均高程为554 m,抵偿投影高程面取值测区平均高程附近值550 m,则高程面投影变形系数为:
| $ \begin{aligned} &\beta=-H_{\Delta} / R_{H} \\ &\beta_{\text {最高点 }}=-(709-550) / 6368000=-1 / 40050 \\ &\beta_{\text {最低点 }}=-(484-550) / 6368000=1 / 96484 \end{aligned} $ |
同理可知,所取高程面投影变形系数绝对值都小于1/20 000,说明YD13~YD34高程抵偿面的选择合理。
2.2 分段独立坐标系投影改正及中央子午线的确定分段测区高程抵偿面保持不变,不同投影带是因为选择了不同经度的中央子午线的原因,如果合理选择中央子午线的位置,使测区边长投影到某一投影带所产生的变形,恰好抵偿这一长度投影到抵偿高程面所产生的变形,这种能抵偿长度变形的投影带为“抵偿投影带”[12]。
根据长度综合变形式(3)和投影综合改正相对误差δ/S≤1/20 000,确定中央子午线点位横坐标西面与起点横坐标的差值,得到移动中央子午线横坐标,根据高斯投影坐标反算公式可由(x,y)推出(B,L),见式(5),须满足以下3个条件(见图 6):①x坐标轴投影后为中央子午线是投影的对称轴;② x坐标轴投影后长度不变;③投影具有正形性质,即正形投影条件。
| $ \left\{\begin{array}{c} B=B_{f}-\frac{t_{f}}{2 M_{f} N_{f}} y^{2}+\frac{t_{f}}{24 M_{f} N_{f}^{3}}\left(5+3 t_{f}^{2}+\eta_{f}^{2}-9 \eta_{f}^{2} t_{f}^{2}\right) y^{4}- \\ \frac{t_{f}}{720 M_{f} N_{f}^{5}} y\left(61+90 t_{f}^{2}+45 t_{f}^{4}\right) y^{6} \\ l=\frac{y}{N_{f} \cos B_{f}}-\frac{y^{3}}{6 N_{f}^{3} \cos B_{f}}\left(1+2 t_{f}^{2}+\eta_{f}^{2}\right)+ \\ \frac{y^{5}}{120 N_{f}^{5} \cos B_{f}}\left(5+28 t_{f}^{2}+24 t_{f}^{4}+6 \eta_{f}^{2}+8 \eta_{f}^{2} t_{f}^{2}\right) \end{array}\right. $ | (5) |
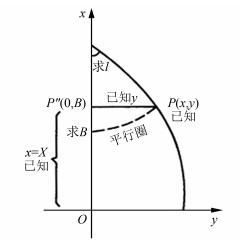 |
| 图 6 高斯投影 Fig.6 Gaussian Projection |
式中,Bf为反算坐标点垂足纬度。高斯投影坐标反算计算过程比较复杂,可以通过Excel编程计算求得,在此不作具体阐述。本文中引大济岷工程的中央子午线经度计算采用华测CGO软件,通过坐标平移后计算求得,各段中央子午线的确定分别如表 2、表 3、表 4所示。
| 表 2 YD01~YD08中央子午线确定表 Tab.2 YD01~YD08 Central Meridian Determination Table |
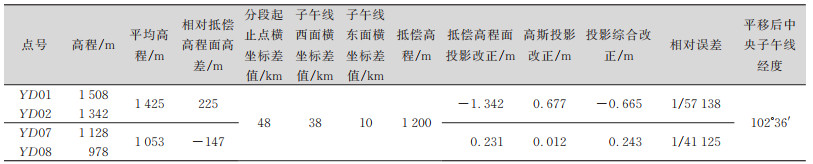 |
| 表 3 YD07~YD14中央子午线确定表 Tab.3 YD07~YD14 Central Meridian Determination Table |
 |
| 表 4 YD13~YD34中央子午线确定表 Tab.4 YD13~YD34 Central Meridian Determination Table |
 |
3 测区实测边长与独立坐标系平差边长比较
由于引大济岷工程GPS控制点作为首级网,GPS控制点彼此不通视,无法利用全站仪观测边对平差边长进行检验,因此下面采用两种全站仪近似边长对平差边长进行检校,如表 5~表 10所示。
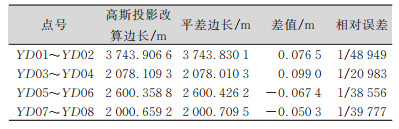
| 表 5 YD01~YD08测区测点高斯边长投影到边长平均高程面对比 Tab.5 YD01~YD08 Survey Point Gauss Side Length Projection to Side Length Average Elevation Comparison |
 |
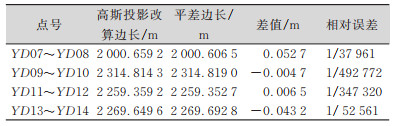
| 表 6 YD08~YD14测区测点高斯边长投影到边长平均高程面对比 Tab.6 YD08~YD14 Survey Point Gauss Side Length Projection to Side Length Average Elevation Comparison |
 |
| 表 7 YD14~YD34测区测点高斯边长投影到边长平均高程面对比 Tab.7 YD14~YD34 Survey Point Gauss Side Length Projection to Side Length Average Elevation Comparison |
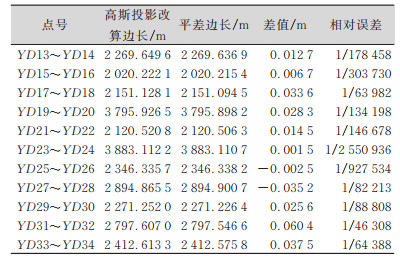 |
| 表 8 YD01~YD08测区GPS基线解算椭球平距对比 Tab.8 Ellipsoid Horizontal Distance Comparison of GPS Baseline Calculation in YD01~YD08 Survey Area |
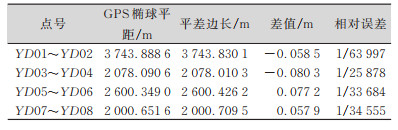 |
| 表 9 YD08~YD14测区GPS基线解算椭球平距对比 Tab.9 Ellipsoid Horizontal Distance Comparison of GPS Baseline Calculation in YD08~YD14 Survey Area |
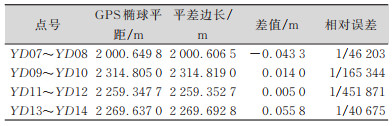 |
| 表 10 YD14~YD34测区GPS基线解算椭球平距对比 Tab.10 Ellipsoid Horizontal Distance Comparison of GPS Baseline Calculation in YD14~YD34 Survey Area |
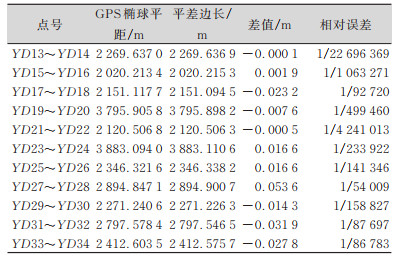 |
1)高斯边长投影到平均高程面的边长比较。
根据
| $ D_{s}=2 D_{G} R(R+H) /\left(2 R^{2}+Y_{m}^{2}\right) $ | (6) |
式中,Ds为归算至测点平均高程面上的边长;DG为高斯平面边长;Sm为参考椭球面边长;R为测区中心处的平均曲率半径,本测区中取R=6 368 km;Ym为边长两端点的横坐标平均数;H为边长两端点的平均高程。
2)利用GPS基线解算椭球平距进行对比。
通过高斯边长投影到边长平均高程面的改算,以及GPS基线解算椭球平距与平差边长的对比,边长的相对误差都小于1/20 000,说明本测区分段独立坐标系的抵偿高程面和中央子午线的移动很好地抑制了测区长度变形。这种方法受测区长度和高差限制比较大,而引大济岷工程测区长,测区东西走向,高差大,采用分段选择抵偿高程面投影和移动中央子午线相结合的方法来解决投影的综合变形,本方法易被测绘人员掌握,斜轴墨卡托投影也能解决投影变形问题,但投影前期计算相对复杂,不易掌握。
4 结束语大型水利工程中,通常采用高斯投影和移动中央子午线的方法来解决测区长度变形,本文对引大济岷工程分段合理地选择投影带和投影面进行了浅析。由于测区处于跨带区域,先要确定测区横坐标到所处带中央子午线的距离,从高斯投影变形大小,确定是否进行换带计算,以减小高斯投影的变形对测区已有地形图使用的影响。在抵偿高程面投影的选择时,宜选分段测区平均高程来做投影抵偿高程面,这有利于测区投影变形均匀,使测区投影长度变形值不大于5 cm/km(即相对误差为1/20 000),满足《水利水电工程测量规范》SL197-2013的要求。本文的方法适合GPS点不通视,无法使用全站仪边长进行检验的工程。
| [1] |
中华人民共合国水利部. 水利水电工程测量规范: SL197-2013[S]. 北京: 中国水利水电出版社, 2013
|
| [2] |
范一中. 再谈工程投影面的最佳选取问题[J]. 测绘通报, 2003(8): 46-47. |
| [3] |
唐基文, 何鹏, 李太平. 地方独立坐标系采用抵偿高程面的任意带高斯投影的分析[J]. 测绘空间地理信息, 2012, 35(8): 186-189. |
| [4] |
马立华. 柴北缘绿北-库南项目区GPS控制网抵偿高程面的选择[J]. 青海科技术与创新, 2010, 17(5): 37-40. |
| [5] |
吴国荣, 章东保, 陈龙邦. 投影于抵偿高程面上的坐标计算方法及其公式推导[J]. 科技创新导报, 2007(34): 39-41. |
| [6] |
孙小荣, 袁涛, 张书毕, 等. 工程测量中电磁波测距边归算方法研究[J]. 测绘通报, 2013(8): 65-67. |
| [7] |
池军锋. 浅析公路路线测量投影面与投影带的选择方法[J]. 中国高新技术企业, 2009, 135(24): 175-176. |
| [8] |
白忠志, 赵晓明, 张晓锋. 论投影面与投影带的选择对控制网的精度影响[J]. 黑龙江测绘, 1995(2): 8-9. |
| [9] |
鞠博晓, 赵文, 陈渠森, 等. 一种基于SRTM高程数据的可视化选取投影面的新方法[J]. 测绘地理信息, 2019, 44(6): 41-43. |
| [10] |
武江伟, 高红光, 朴盛莲, 等. 长距离供水工程测量平面坐标系的选择[J]. 测绘地理信息, 2015, 40(3): 74-76. |
| [11] |
林华健. 基于最小二乘的具有高程抵偿面的任意带高斯投影变换方法研究[J]. 测绘地理信息, 2017, 42(3): 34-36. |
| [12] |
康世英. 基于国家坐标系的独立坐标系建立新方法[J]. 测绘地理信息, 2018, 43(5): 58-60. |
 2022, Vol. 47
2022, Vol. 47

