| 地面三维激光扫描仪系统误差模型研究及精度分析 |
2. 武汉大学灾害监测和防治研究中心,湖北 武汉,430079;
3. 重庆大学土木工程学院,重庆,400030
2. Hazard Monitoring & Prevention Research Center, Wuhan University, Wuhan 430079,China;
3. School of Civil Engineering, Chongqing University, Chongqing 400030,China
地面三维激光测量技术突破了传统单点测量的方法,通过扫描可获得每秒数万点的高精度点云数据[1]。随着这项技术在科学研究、工业生产等领域的广泛应用,工程项目对其测量精度也提出了较高的要求[2]。地面三维激光扫描仪的系统参数是由厂家在理想状况下测量并给定,受仪器构造及生产过程的不确定因素影响,导致仪器实际指标与标称不一致,给测量带来误差。为了快速获取系统误差的改正参数,并利用这些参数对测量数据进行系统性偏差改正,可对三维激光扫描仪系统误差进行建模和标定分析。张毅等[3]提出的11参数自检校法未考虑外部观测条件因素对激光测距的影响,本文在地面三维激光扫描仪系统误差影响因素的基础上,对激光测距误差进行深入研究,提出了11参数自检校法的优化模型,利用稳定性好、精度高和计算速度快的罗德里格矩阵求解模型参数[4],详细地给出了模型解算策略。
1 系统误差模型 1.1 自检校法自检校法是以空间相似变换为基础,由11个待定参数构成地面三维激光扫描系统误差模型[5],其中6个为外部定向参数,另外5个为仪器系统误差参数。式(1) 为自检校法模型:
| $\begin{align} & {{\mathbf{F}}_{XYZ}}=\left[ \begin{matrix} X \\ Y \\ Z \\ \end{matrix} \right]=\lambda \cdot \mathbf{R}\left( \Phi ,\Omega ,K \right) \\ & \left[ \begin{matrix} \left( S+k+S\cdot r \right)\cos \left( \theta +w \right)\cos \left( \alpha +\frac{i}{\cos \theta }+j\tan \theta \right) \\ \left( S+k+S\cdot r \right)\cos \left( \theta +w \right)\sin \left( \alpha +\frac{i}{\cos \theta }+j\tan \theta \right) \\ \left( S+k+S\cdot r \right)\sin \left( \theta +w \right) \\ \end{matrix} \right]+\left[ \begin{matrix} \Delta X \\ \Delta Y \\ \Delta Z \\ \end{matrix} \right] \\ \end{align}$ | (1) |
式中,k为三维激光测距加常数改正量;r为三维激光测距乘常数改正系数[4]。当k=0时,地面三维激光扫描仪为相位式测距;当r=0时,则为脉冲式测距。R(Φ,Ω,Κ)为旋转矩阵;[ΔX ΔY ΔZ]T为空间直角坐标转换平移量;λ为缩放因子,不作为系统误差参数;i、j、w分别为视准轴误差、水平轴误差、竖角指标差;间接观测量S、α和θ可通过三维激光扫描仪测量的坐标点计算得到[6]。
该模型对测距S进行了加常数和乘常数改正,同时也考虑了视准轴误差和水平轴误差对测角的影响,通过改正后的三个间接观测值重新计算扫描点坐标。但该模型对距离S进行误差改正时,只考虑了激光测距方式[7]所引起的误差,未考虑测量时外部观测条件对激光测距的影响。
1.2 模型优化地面三维激光扫描仪的测距误差受激光测距方式和外部观测条件影响,对外部观测条件而言其误差主要是由非线性状态、时间漂移、温度漂移、混合像素等因素引起的[8],可表示为:
| $\begin{align} & \Delta {{S}_{inst}}\text{=}{{a}_{0}}+{{a}_{1}}t+{{a}_{2}}{{e}^{-{{a}_{3}}T}}+\Delta {{S}_{walk}}+ \\ & \left( {{m}_{0}}+{{m}_{1}}t+{{m}_{2}}{{t}^{2}}+{{m}_{3}}{{t}^{3}} \right)S+\left( b\cdot y \right)S \\ & +\left( c\cdot {{e}^{-{{c}_{1}}t}} \right)S+{{d}_{1}}{{S}^{2}}+{{d}_{2}}{{S}^{3}}+{{d}_{3}}{{S}^{4}}+{{d}_{4}}{{S}^{5}}+\cdots \\ \end{align}$ | (2) |
式中,ΔSinst为测距误差;t为温度;T为地面三维激光扫描仪开机时长;y为扫描仪的使用年份;ΔSwalk为时间漂移误差;m0、m1、m2、m3为尺度因子;b为时间效应比例因子;c和c1为测距和温度比例因子;最后4项为非线性距离制约误差;其余参数为扫描仪校准系数。
本文将ΔSinst作为一项改正参数,对激光测距误差作进一步改正,式(3) 为优化后的自检校法模型:
| $\begin{align} & {{\mathbf{F}}_{XYZ}}=\left[ \begin{matrix} X \\ Y \\ Z \\ \end{matrix} \right]=\lambda \cdot \mathbf{R}\left( \Phi ,\Omega ,K \right) \\ & \left[ \begin{matrix} \left( S+k+\left( S\text{+}\Delta {{S}_{inst}} \right)\cdot r \right)\cos \left( \theta +w \right)\cos \left( \alpha +\frac{i}{\cos \theta }+j\tan \theta \right) \\ \left( S+k+\left( S\text{+}\Delta {{S}_{inst}} \right)\cdot r \right)\cos \left( \theta +w \right)\sin \left( \alpha +\frac{i}{\cos \theta }+j\tan \theta \right) \\ \left( S+k+\left( S\text{+}\Delta {{S}_{inst}} \right)\cdot r \right)\sin \left( \theta +w \right) \\ \end{matrix} \right]+\left[ \begin{matrix} \Delta X \\ \Delta Y \\ \Delta Z \\ \end{matrix} \right] \\ \end{align}$ | (3) |
式中,k=k′+ΔSinst。
测距误差一部分为激光测距方式引起的,另一部分为环境因素的影响。考虑到模型中测距误差ΔSinst和k之间存在关联性,将二者作为整体,即加常数k和环境因素ΔSinst作为一个独立的参数k。
1.3 模型解算利用Taylor级数将式(3) 展开,保留一次项,ΔSinst和加常数合并后的线性展开式中含有11个待定参数。
对待定参数分别求偏导数得:
| $\begin{align} & \frac{\partial {{\mathbf{F}}_{XYZ}}}{\partial k}=\lambda \cdot \mathbf{R}\left( {{\Phi }^{0}},{{\Omega }^{0}},{{K }^{0}} \right)\cdot \\ & \left[ \begin{matrix} \cos \left( \theta +{{w}^{0}} \right)\cos \left( \alpha +\frac{{{i}^{0}}}{\cos \theta }+{{j}^{0}}\tan \theta \right) \\ \cos \left( \theta +{{w}^{0}} \right)\sin \left( \alpha +\frac{{{i}^{0}}}{\cos \theta }+{{j}^{0}}\tan \theta \right) \\ \sin \left( \theta +{{w}^{0}} \right) \\ \end{matrix} \right] \\ \end{align}$ | (4) |
同理,可求出
对旋转矩阵求偏导数得:
| $\begin{align} & \frac{\partial {{\mathbf{F}}_{XYZ}}}{\partial \Phi }=\lambda \cdot \\ & \left[ \begin{matrix} 0 & 0 & 0 \\ \sin \Phi \sin K +\cos \Phi \sin \Omega \cos K & -\sin \Phi \cos K +\cos \Phi \sin \Omega \sin K & \cos \Phi \cos \Omega \\ \cos \Phi \sin K -\sin \Phi \sin \Omega \sin K & -\cos \Phi \cos K -\sin \Phi \sin \Omega \sin K & -\sin \Phi \cos \Omega \\ \end{matrix} \right]\left[ \begin{matrix} X_{S}^{0} \\ Y_{S}^{0} \\ Z_{S}^{0} \\ \end{matrix} \right] \\ \end{align}$ | (5) |
同理,可求出
对平移参数ΔX求偏导数得:
| $\frac{\partial {{\mathbf{F}}_{XYZ}}}{\partial \Delta X}={{\left[ \begin{matrix} 1 & 0 & 0 \\ \end{matrix} \right]}^{T}}$ | (6) |
同理,可求出
将以上所求的偏导数构成系数矩阵B,每个偏导数为3×1的子矩阵,则系数矩阵B从标靶1到标靶n可表示为:
| $\begin{align} & \underset{3n\times 11}{\mathop{\mathbf{B}}}\,= \\ & \left[ \begin{matrix} \frac{\partial \mathbf{F}_{X}^{1}}{\partial k} & \frac{\partial \mathbf{F}_{X}^{1}}{\partial r} & \frac{\partial \mathbf{F}_{X}^{1}}{\partial w} & \frac{\partial \mathbf{F}_{X}^{1}}{\partial i} & \frac{\partial \mathbf{F}_{X}^{1}}{\partial j} & \frac{\partial \mathbf{F}_{X}^{1}}{\partial \Phi } & \frac{\partial \mathbf{F}_{X}^{1}}{\partial \Omega } & \frac{\partial \mathbf{F}_{X}^{1}}{\partial K } & \frac{\partial \mathbf{F}_{X}^{1}}{\partial \Delta X} & \frac{\partial \mathbf{F}_{X}^{1}}{\partial \Delta Y} & \frac{\partial \mathbf{F}_{X}^{1}}{\partial \Delta Z} \\ \frac{\partial \mathbf{F}_{Y}^{1}}{\partial k} & \frac{\partial \mathbf{F}_{Y}^{1}}{\partial r} & \frac{\partial \mathbf{F}_{Y}^{1}}{\partial w} & \frac{\partial \mathbf{F}_{Y}^{1}}{\partial i} & \frac{\partial \mathbf{F}_{Y}^{1}}{\partial j} & \frac{\partial \mathbf{F}_{Y}^{1}}{\partial \Phi } & \frac{\partial \mathbf{F}_{Y}^{1}}{\partial \Omega } & \frac{\partial \mathbf{F}_{Y}^{1}}{\partial K } & \frac{\partial \mathbf{F}_{Y}^{1}}{\partial \Delta X} & \frac{\partial \mathbf{F}_{Y}^{1}}{\partial \Delta Y} & \frac{\partial \mathbf{F}_{Y}^{1}}{\partial \Delta Z} \\ \frac{\partial \mathbf{F}_{Z}^{1}}{\partial k} & \frac{\partial \mathbf{F}_{Z}^{1}}{\partial r} & \frac{\partial \mathbf{F}_{Z}^{1}}{\partial i} & \frac{\partial \mathbf{F}_{Z}^{1}}{\partial i} & \frac{\partial \mathbf{F}_{Z}^{1}}{\partial j} & \frac{\partial \mathbf{F}_{Z}^{1}}{\partial \Phi } & \frac{\partial \mathbf{F}_{Z}^{1}}{\partial \Omega } & \frac{\partial \mathbf{F}_{Z}^{1}}{\partial K } & \frac{\partial \mathbf{F}_{Z}^{1}}{\partial \Delta X} & \frac{\partial \mathbf{F}_{Z}^{1}}{\partial \Delta Y} & \frac{\partial \mathbf{F}_{Z}^{1}}{\partial \Delta Z} \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ \begin{matrix} \frac{\partial \mathbf{F}_{X}^{n}}{\partial k} \\ \frac{\partial \mathbf{F}_{Y}^{n}}{\partial k} \\ \frac{\partial \mathbf{F}_{Z}^{n}}{\partial k} \\ \end{matrix} & \begin{matrix} \frac{\partial \mathbf{F}_{X}^{n}}{\partial r} \\ \frac{\partial \mathbf{F}_{Y}^{n}}{\partial r} \\ \frac{\partial \mathbf{F}_{Z}^{n}}{\partial r} \\ \end{matrix} & \begin{matrix} \frac{\partial \mathbf{F}_{X}^{n}}{\partial w} \\ \frac{\partial \mathbf{F}_{Y}^{n}}{\partial w} \\ \frac{\partial \mathbf{F}_{Z}^{n}}{\partial w} \\ \end{matrix} & \begin{matrix} \frac{\partial \mathbf{F}_{X}^{n}}{\partial i} \\ \frac{\partial \mathbf{F}_{Y}^{n}}{\partial i} \\ \frac{\partial \mathbf{F}_{Z}^{n}}{\partial i} \\ \end{matrix} & \begin{matrix} \frac{\partial \mathbf{F}_{X}^{n}}{\partial j} \\ \frac{\partial \mathbf{F}_{Y}^{n}}{\partial j} \\ \frac{\partial \mathbf{F}_{Z}^{n}}{\partial j} \\ \end{matrix} & \begin{matrix} \frac{\partial \mathbf{F}_{X}^{n}}{\partial \Phi } \\ \frac{\partial \mathbf{F}_{Y}^{n}}{\partial \Phi } \\ \frac{\partial \mathbf{F}_{Z}^{n}}{\partial \Phi } \\ \end{matrix} & \begin{matrix} \frac{\partial \mathbf{F}_{X}^{n}}{\partial \Omega } \\ \frac{\partial \mathbf{F}_{Y}^{n}}{\partial \Omega } \\ \frac{\partial \mathbf{F}_{Z}^{n}}{\partial \Omega } \\ \end{matrix} & \begin{matrix} \frac{\partial \mathbf{F}_{X}^{n}}{\partial K } \\ \frac{\partial \mathbf{F}_{Y}^{n}}{\partial K } \\ \frac{\partial \mathbf{F}_{Z}^{n}}{\partial K } \\ \end{matrix} & \begin{matrix} \frac{\partial \mathbf{F}_{X}^{n}}{\partial \Delta X} \\ \frac{\partial \mathbf{F}_{Y}^{n}}{\partial \Delta X} \\ \frac{\partial \mathbf{F}_{Z}^{n}}{\partial \Delta X} \\ \end{matrix} & \begin{matrix} \frac{\partial \mathbf{F}_{X}^{n}}{\partial \Delta Y} \\ \frac{\partial \mathbf{F}_{Y}^{n}}{\partial \Delta Y} \\ \frac{\partial \mathbf{F}_{Z}^{n}}{\partial \Delta Y} \\ \end{matrix} & \begin{matrix} \frac{\partial \mathbf{F}_{X}^{n}}{\partial \Delta Z} \\ \frac{\partial \mathbf{F}_{Y}^{n}}{\partial \Delta Z} \\ \frac{\partial \mathbf{F}_{Z}^{n}}{\partial \Delta Z} \\ \end{matrix} \\ \end{matrix} \right] \\ \end{align}$ |
然后计算出误差方程常数项L,每个标靶点的误差方程常数项为3×1的子矩阵,常数项矩阵L从标靶1到标靶n可表示为:
| $\underset{3n\times 1}{\mathop{\mathbf{V}}}\,=\underset{3n\times 11}{\mathop{\mathbf{B}}}\,\cdot \underset{11\times 1}{\mathop{x}}\,-\underset{3n\times 1}{\mathop{\mathbf{L}}}\,$ | (7) |
式中,
假设实验中共有n对同名标靶点参与自检校模型的解算,则共有3n个误差方程,利用间接平差可得待定参数的改正数为:
| $x={{\left( {{\mathbf{B}}^{T}}\mathbf{B} \right)}^{-1}}{{\mathbf{B}}^{T}}\mathbf{L}$ | (8) |
式(3) 的线性展开式中含有自检校模型的待定参数,因此需确定待定参数的初值并采用迭代法进行计算。
对于初值问题,优化后的自检校模型中有6个外部定向参数,假设三维激光扫描仪无系统误差,在此条件下由式(1) 对同名点进行空间坐标转换,获取旋转矩阵R(Φ,Ω,Κ)、平移矩阵[ΔX ΔY ΔZ]T的初值和缩放因子λ的值,另5个待定参数为系统内部参数,其值较小,假设仪器制造商在设备调试时已消除其影响,则可令其初值为0[9]。采用式(8) 进行迭代计算,当待定参数改正数均小于设定阈值时停止迭代,将未知数的初始值和改正数累加即为未知数的最终值[8]。
| $x={{x}_{0}}+{{x}_{1}}+{{x}_{2}}+\cdots +{{x}_{n}}$ | (9) |
式中,x0为待定参数初始值;x1、x2、…、xn为迭代计算时待定参数的改正数。
利用式(9) 得到各参数的最终值,结合式(3) 计算经系统误差改正后的扫描点坐标,并将改正后的扫描点坐标通过空间相似变换转换至全站仪的绝对坐标系下,同全站仪所测量的同名点标靶坐标进行比较和分析。
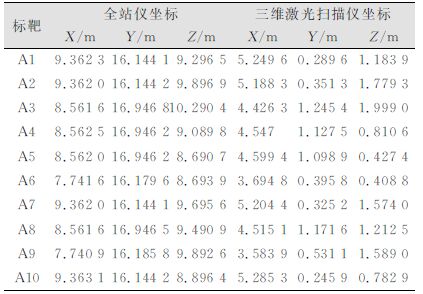
2 实验设计与结果分析为了验证优化后的自检校法模型的可靠性与正确性,以RIEGL VZ-400地面三维激光扫描仪(测距精度±5 mm,测角精度±1.8″)为实验对象,对其系统误差进行研究和分析。在实验场地中均匀有层次地布设了10个标靶并对其进行编号。首先使用三维激光扫描仪对实验场地进行扫描,并对标靶点进行精扫描,利用该扫描仪的配套软件RISCAN PRO对数据进行处理,获取标靶区域的点云数据,根据点云数据的强度信息采用阈值分割的方法得到标靶区域,对标靶区域点云数据进行强度加权拟合,获取标靶几何中心在三维激光扫描仪下的坐标。然后采用测量精度优于RIEGL VZ-400的Leica TCRP1201全站仪(测距精度±1 mm,测角精度为±1″)对准反射贴片的十字中心,获取同名点标靶在独立坐标系下的几何中心坐标,并以此作为绝对坐标对扫描仪进行系统误差检校。表 1为扫描仪和全站仪获取的三维坐标。
| 表 1 标靶在扫描仪和全站仪下的坐标 Table 1 Coordinate of Targets Under Terrestrial Laser Scanning and Total Station |
 |
不考虑三维激光扫描仪内部系统误差时,将表 1中的A1-A5作为模型参数计算点,利用其标靶坐标可求出三维激光扫描仪内部坐标系转换至全站仪坐标系的缩放因子、旋转矩阵和平移参数。缩放因子λ为1.000 089,旋转矩阵为:
| $\mathbf{R}=\left[ \begin{matrix} \text{0}\text{.99027} & \text{-0}\text{.08118} & \text{0}\text{.11302} \\ \text{0}\text{.09159} & \text{0}\text{.99169} & \text{-0}\text{.09029} \\ \text{-0}\text{.10475} & \text{0}\text{.09977} & \text{0}\text{.98948} \\ \end{matrix} \right]$ |
平移参数为:
| $\left[ \begin{matrix} \Delta X \\ \Delta Y \\ \Delta Z \\ \end{matrix} \right]=\left[ \begin{matrix} \text{4}\text{.03955} \\ \text{15}\text{.45144} \\ \text{8}\text{.62767} \\ \end{matrix} \right]$ |
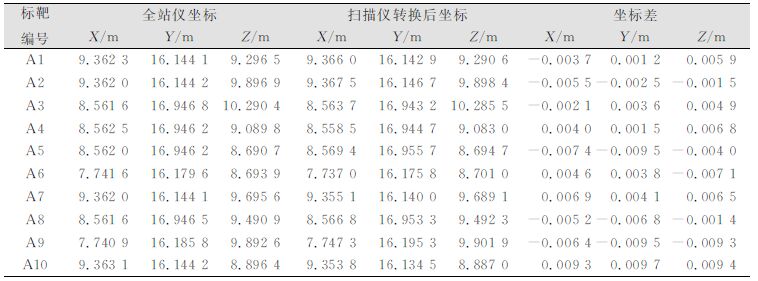
通过以上的7个参数(缩放因子λ未参与迭代计算),将三维激光扫描仪的坐标全部转换至全站仪的绝对坐标系下,并与全站仪测量的标靶坐标进行比较,结果见表 2,其中A6-A10为模型参数检核点。
| 表 2 扫描仪转换后坐标与全站仪坐标之差比较 Table 2 Comparison of Transformed Coordinate Under Terrestrial Laser Scanning to Total Station |
 |
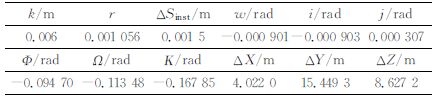
考虑地面三维激光扫描仪系统误差后,利用A1-A5号标靶坐标并根据式(8) 可计算出各系统误差参数。实际测量时环境因素对激光测距的影响小于激光测距方式的影响,根据实验数据的多次组合,当二者权值为1∶3时效果较为理想,从而获得ΔSinst的具体数值,结果见表 3。
利用表 3中的模型参数通过式(3) 对三维激光扫描仪测量的A1-A10标靶坐标进行改正,并利用空间相似变换将改正后的标靶坐标转换至全站仪坐标系下,与全站仪测量的标靶坐标进行比较和分析,结果见表 4。
| 表 3 三维激光扫描仪系统参数 Table 3 System Parameters in Terrestrial Laser Scanning |
 |
| 表 4 扫描仪经系统误差参数改正转换后坐标与全站仪坐标之差比较 Table 4 Ccoordinate Comparison Between Terrestrial Laser Scanning Which Corrected by System Error Parameters and Total Station |
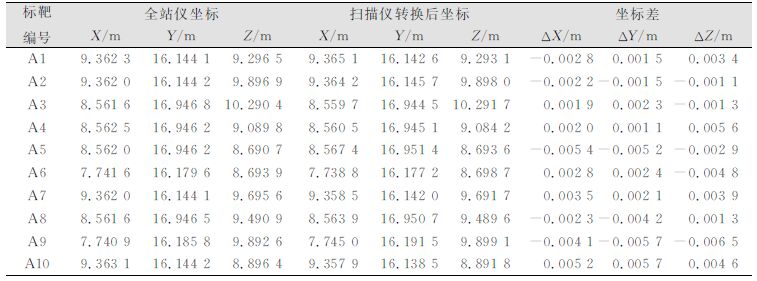 |
由表 2和表 4可以看出:地面三维激光扫描仪经系统误差参数改正转换后坐标与全站仪坐标之差与未经系统误差参数改正转换后坐标与全站仪坐标之差相比,数值上各标靶点的X、Y、Z 3个方向明显减少。在不考虑全站仪坐标测量误差时,根据表 2的数据计算,对于模型参数计算点,X、Y、Z方向中误差和点位中误差分别为0.004 9 m、0.004 8 m、0.005 0 m和0.008 4 m;对于模型参数检核点,X、Y、Z方向中误差和点位中误差分别为0.006 9 m、0.007 2 m、0.007 3 m和0.012 3 m。根据表 4数据计算,对于模型参数计算点,X、Y、Z方向中误差和点位中误差分别为0.002 0 m、0.001 5 m、0.003 0 m和0.004 0 m;对于模型参数检核点,X、Y、Z方向中误差和点位中误差分别为0.003 5 m、0.004 2 m、0.004 0 m和0.006 8 m。由此可见,模型参数检核点经系统误差改正后点位精度提高约45%,反映出三维激光扫描仪误差的系统性,也证明了优化后的系统误差模型可以提高扫描仪测量数据精度。
3 结束语本文研究了三维激光扫描仪测距时系统误差的来源,分析了系统误差对激光测距的影响。以地面三维激光扫描仪的观测方程为载体对11参数自检校法提出了优化模型,引入外部条件综合影响因子ΔSinst,并对激光测距进行改正。详细推导了公式,并通过实验验证了优化模型的正确性与可靠性。从实验结果可以看出,经过系统误差改正后,RIEGL VZ-400地面三维激光扫描仪的数据质量有了很大的提高,从而验证了系统误差模型的可行性与正确性,为促进地面三维激光扫描仪系统误差检校体系的发展和完善提供了参考。
| [1] |
唐琨, 花向红, 魏成, 等. 基于三维激光扫描的建筑物变形监测方法研究[J].
测绘地理信息,2013,38(2) : 54–55.
Tang Kun, Hua Xianghong, Wei Cheng, et al. The Experimental Study of Buildings Deformation Monitoring Method Based on 3D Laser Scanning[J]. Journal of Geomatics,2013,38(2) : 54–55. |
| [2] | Yu Jinxia, Cai Zixing, Duan Zhuohua. Improved Method for the Feature Extraction of Laser Scanner Using Genetic Clustering[J]. Journal of Systems Engineering and Electronics,2008,19(2) : 280–285. DOI:10.1016/S1004-4132(08)60079-1 |
| [3] |
张毅, 闫利, 杨红, 等. 地面三维激光扫描的系统误差模型研究[J].
测绘通报,2012,(1) : 16–19.
Zhang Yi, Yan Li, Yang Hong, et al. Research on Systematic Error Model of Terrestrial Laser Scanning[J]. Bulletin of Surveying and Mapping,2012,(1) : 16–19. |
| [4] |
田茂, 花向红, 丁鸽, 等. 基于罗德里格矩阵的混合最小二乘方法在三维激光中的应用[J].
测绘地理信息,2014,39(2) : 18–21.
Tian Mao, Hua Xianghong, Ding Ge, et al. Three-Dimensional Laser Scanning Technology Research Application Based on Mixed Least Squares in Rodrigue Matrix[J]. Journal of Geomatics,2014,39(2) : 18–21. |
| [5] | Guan Y L, Cheng X J, Zhan X W, et al. Research on Systematic Errors Calibration of Terrestrial Laser Scanner[J]. Acta Geodaetica et Cartographica Sinica,2014,43(7) : 731–738. |
| [6] |
高宝华, 蒋理兴, 郭连惠, 等. 地面三维激光扫描仪自检校方法研究[J].
海洋测绘,2012,(5) : 45–48.
Gao Baohua, Jiang Lixing, Guo Lianhui, et al. Study on the Self-check Calibration Method of the Laser Scanner[J]. Hydrographic Surveying and Charting,2012,(5) : 45–48. |
| [7] | Nguyen T T, Guo X, Liu X G. Analysis of Error Sources in Terrestrial Laser Scanning [C]. Applications and the 6th 3D GeoInfo Conference, Wuhan, China, 2011 |
| [8] | Reshetyuk Y. Self-calibration and Direct Georeferencing in Terrestrial Laser Scanning [D]. Sweden: University of Gävle, 2009 |
| [9] | 张启福,孙现申,李宗春. 基于人工标志的三维激光扫描仪自检校方法研究[C]. 全国工程测量2012技术研讨交流会,中国测绘学会工程测量分会,沈阳, 2012 Zhang Qifu, Sun Xianshen, Li Zongchun. Study on the Self-check Calibration Method of the Laser Scanner Based on Artificial Target[C].Technical Seminar of National Engineering Surveying 2012 at the Chinese Academy of Surveying and Mapping Engineering Survey Section, Shenyang, China, 2012 |
 2016, Vol. 41
2016, Vol. 41


