| 机载激光点云单一屋顶边缘自动提取算法研究 |
在基于机载激光点云的城市建筑物三维重建中,屋顶面边缘的精确与自动提取是实现自动化建筑物三维重建的关键技术之一。
Ronald[1]提出了格雷汉姆扫描算法(Graham-Scan),用于提取平面点集的凸包,该方法能够准确地提取凸多边形的边缘,但在解决凹边缘提取问题时失效。基于不规则三角网的边缘检测算法[2]首先定义三角网的最大边长[3],对点集进行构网之后,删除超过最大边长的边,再提取三角网的边缘。这种方法需要构建Delaunay三角网,耗费时间较长。沈蔚等[4]采用α-shapes算法提取点集边缘,该方法原理是假设一个半径为α的圆在点集外滚动,其滚动的痕迹就是点集的边缘。当α值很小,则每个点都是边缘点;当α值很大,则检测结果为点集的凸包。该方法需要多次判断点是否落在圆内,计算量较大[5]。陈涛等[6]提出一种使用搜索盒搜索平面离散点集边缘点的算法,该方法将离散点分配到搜索盒中,遍历位于边界的搜索盒,将其中的点连接成边缘点链表。该搜索算法适应性强,但该方法过度依赖搜索盒边长并难以准确确定搜索方向,在点云分布不均匀时,该方法的边缘提取结果也不理想。此外,常用的边缘检测算法还包括将点云经过重采样转化为影像,使用影像边缘检测的方法进行边缘提取[7],此类方法在重采样过程中会损失边缘的精度,无法得到准确的边界信息。
本文采用主成分分析(principle component analysis,PCA)算法将原始点云变换到主平面,通过格网进行边缘粗提取,得到概略边界,在此基础上,使用改进的α-shapes对边缘进行精化,得到最终的准确边缘。本文边缘提取算法参数选取不依赖于输入的数据,适用性广。
1 主平面投影由于建筑物的屋顶面与地面之间并不一定平行(如人字形屋顶),在倾斜角较大时,若采用水平投影方式将点云投影到水平面上,点云的分布情况发生较大变化,投影后的点云将无法反映原始点云的分布特征[8]。
本文采用PCA算法,将原始点云转换到主平面上。构造点集的协方差矩阵,并求出协方差矩阵的特征值λ1、λ2、λ3及其对应的特征向量ξ1、ξ2、ξ3,并按照特征值的大小排序,即λ1 < λ2 < λ3。取最大的两个特征值对应的特征向量,得到一个3×2的矩阵
通过Pn×2= Pn×3× M3×2将点云投影到主平面上,使用投影后的点云进行进一步处理。其中,Pn×3是投影前原始点云的三维坐标,Pn×2是投影到主平面后的点云二维坐标。
2 格网法边缘粗提取首先,将变换到主平面的屋顶面数据进行格网划分。为了避免出现单元格尺寸太小而产生空洞,单元格尺寸可设置为点云间距的2~3倍,点云间距由经验公式计算[6]。在本文中,通过在点云数据中随机选取k个点,计算r邻域内点数,分别计算出平均间距后取均值作为最终的点云间距。单元格尺寸为:
| $ S = C \times \frac{{\sqrt {\pi {r^2}} }}{k}\sum\limits_{i = 1}^k {{{\left( {{n_i} - 1} \right)}^{ - \frac{1}{2}}}} $ | (1) |
式中, S为单元格尺寸; C为常数; n为点数。
将有点云数据的单元格定义为对象单元格,即图 1中灰色单元格,将无点云数据的单元格定义为背景单元格,将距离网格角点最近的点云标记为屋顶边缘点,依次连接边缘点得到初始边缘。
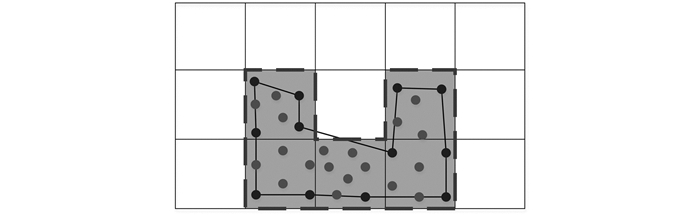 |
| 图 1 格网法边缘粗提取 Fig.1 Rough Extraction of Boundary by Grid Division |
基于格网的边缘提取算法能够鲁棒的提取边缘点,但是通过该算法提取出来的初始边缘只是概略边缘,是真实边缘的近似,而不是精确的边缘。它能产生一个拓扑上正确的多边形边缘,但是无法保证其几何完整性。
3 改进α-shapes算法边缘精提取在格网法边缘粗提取算法中,由于单元格尺寸大于点云间隔,提取的边缘往往是概略边缘,无法满足建筑物自动三维建模的需求。本文使用改进的α-shapes算法对提取的概略边缘进行精化。
本文算法原理与α-shapes算法类似,利用一个在点集外部滚动的圆进行边缘的精提取。传统的α-shapes算法中,圆的半径α固定不变,当其在点集外部滚动时,总保持其仅与点集中的两个点相接,则这两个点为边缘点;当半径α足够小时,出现临界情况,即圆与点集的3个点相接。本文算法与传统α-shapes算法不同的是,圆的半径是可变的。在设置最大角度阈值θmax的前提下,判断在临界情况下,即圆仅与点集的3个点相接时,此时所形成的扇形的圆心角是否小于阈值θmax,若满足条件,则将其判定为边缘点。如图 2所示,线段AB是初始边缘,在点集中任选一点P,同时以线段AB为弦,可构成一个扇形,其圆心角为θ,定义为内缩角,θ为:
| $ \left\{ \begin{align} & \beta =\arccos \left( \frac{\overrightarrow{PA}\times \overrightarrow{PB}}{\left| \overrightarrow{PA} \right|\times \left| \overrightarrow{PB} \right|} \right) \\ & \theta =2\pi -2\beta \\ \end{align} \right. $ | (2) |
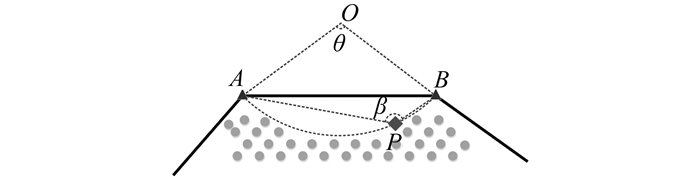 |
| 图 2 边缘精提取 Fig.2 Accurate Extraction of Boundary |
同时定义线段AB和弧AB组成的弓形区域为扫描区域,扫描区域内的点为可能的边缘点。当扇形区域内只存在A、B、P 3个点时,且内缩角θ小于最大角度阈值θmax,可确定P为边缘点。
当θ趋近于0时,弧AB趋近于线段AB,得到的精确边界为AB;当θ>π时,扫描区域大于半圆,就易形成不断内缩的现象,得到边界检测结果就会将内部点作为边界点[9];当θ值从0逐渐增大时,扫描区域和区域内点数也逐渐增大。因此,当线段AB和点P构成的扇形内缩角θ为所有可能的边缘点中最小时,扫描区域内只有A、B、P 3个点,则点P为边缘点,边缘AB可进一步精确到折线APB,采用分治法,将折线APB分成AP和PB,进行进一步的精化,多次迭代,可以不断地接近真实边缘。
由于θ>π会出现将内部点标记为边界点的情况,将内缩角θ是否大于最大角度阈值θmax作为迭代终止的条件。本文中选定的阈值为2π/3。
边缘精提取的具体流程如下:①依次取初始边缘的其中一段AB,计算出在以AB为弦的扫描区域内的点,作为可能的边缘点;②在可能的边缘点中,计算出每个点所对应的内缩角α,找到最小值θmin及其所对应的点P,若θmin大于最大角度阈值,则AB为精确边界,停止迭代;否则,将P标记为边缘点,对AP和PB分别进行边缘精提取,进行迭代。
4 实验与分析本文采用L型屋顶面点云、回型屋顶面点云、圆形屋顶面点云以及双曲面屋顶面点云进行实验,检验本文算法的边缘检测效果,并与传统的α-shapes算法和基于不规则三角网方法进行对比。
1) L型屋顶面边缘提取结果对比如图 3所示。传统的α-shapes算法和基于三角网边缘提取的算法需要人工输入参数,而参数的选择会影响到边缘提取的效果,从图 3(c)和图 3(e)可看出,在参数选取过大时,提取的边缘容易出现失真;从图 3(d)和图 3(f)可看出,在参数选取过小时,提取的边缘容易出现虚假空洞。而本文算法不需要人工选取参数,边缘提取效果良好。
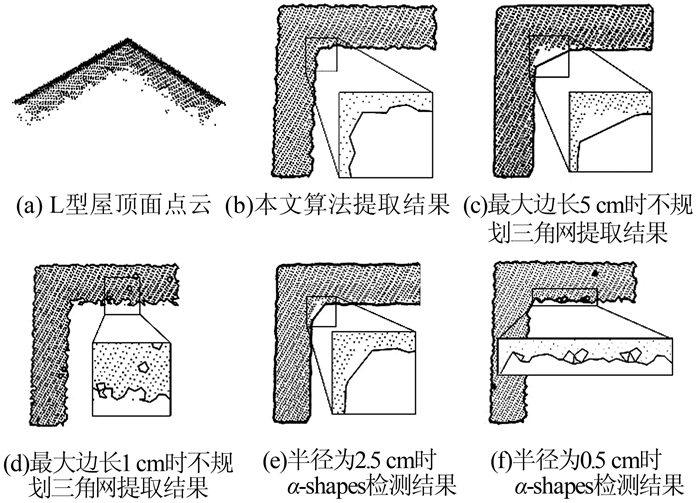 |
| 图 3 L型屋顶面边缘提取结果对比 Fig.3 Contrast of L-Shaped Roof Boundary Extraction |
2) 图 4(a)为本文算法提取结果; 图 4(b)为α-shapes算法提取结果。其中,d为平均点云间隔。在相同参数下,随着点云间隔增加,α-shapes提取效果变差,而本文算法仍能保持较好的结果。基于三角网边缘提取结果与α-shapes结果类似。
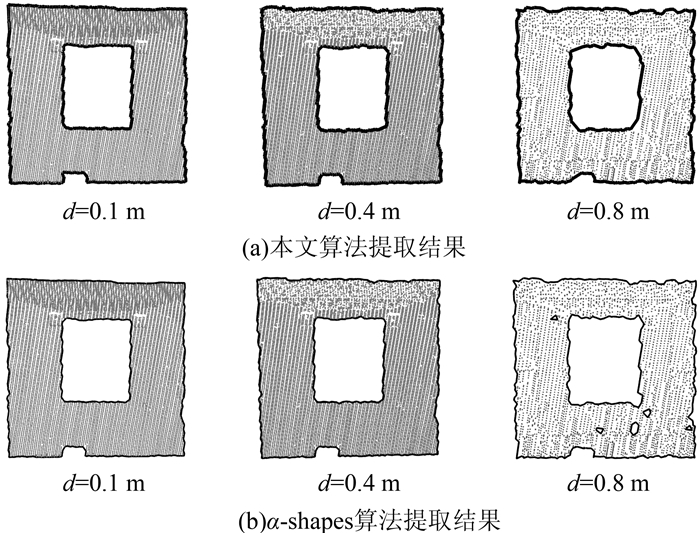 |
| 图 4 回型屋顶面边缘提取结果对比 Fig.4 Contrast of Back-Shaped Roof Boundary Detection |
3) 圆形屋顶面边缘提取结果对比如图 5所示。对于只有凸边缘特征的屋顶面,本文算法和传统的算法都能完美提取出边缘。
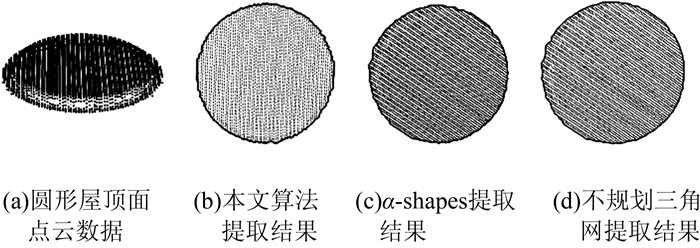 |
| 图 5 圆形屋顶面边缘提取结果对比 Fig.5 Contrast of Circular Roof Boundary Extraction |
4) 双曲面屋顶面边缘提取结果如图 6所示。对于曲面屋顶,本文算法能取得与α-shapes和基于不规则三角网边缘提取一样的结果。
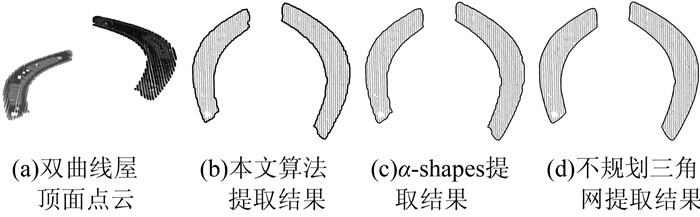 |
| 图 6 双曲面屋顶面边缘提取结果 Fig.6 Result of Double Curved Roof Boundary Detection |
5 结束语
本文提出的屋顶面边缘检测算法,牺牲少量时间将数据进行格网组织,快速排除非边缘单元格,加快搜索速度;采用基于角度最小值的改进的α-shapes算法,相对于α-shapes算法中多次判断点是否在圆内,计算量大大减少。
本文算法能够正确地提取带有空洞的凸多边形、凹多边形、曲面等常见屋顶的边界。α-shapes算法和基于不规则三角网的方法需要在对输入数据有一定了解的基础上进行参数选取,而本文算法中参数选取与输入数据无关,不会因参数选取不合适而提取出错误边缘,对于不同的数据有很好地适应性,同时提取的边缘准确,能实现无人工干预的边缘自动化提取,为城市建筑物的自动化重建提供了可能。
| [1] |
Ronald L. An Efficient Algorith for Determining the Convex Hull of a Finite Planar Set[J]. Information Processing Letters, 1972, 1(4): 132-133. DOI:10.1016/0020-0190(72)90045-2 |
| [2] |
宣贺君, 苗启广, 刘如意, 等. 基于不规则三角网的LiDAR数据的边缘检测新算法[J]. 光学学报, 2014, 34(12): 315-321. |
| [3] |
周秋生, 王延亮, 马俊海. 对TIN模型边界生成算法的研究[J]. 测绘通报, 2005(5): 30-32. DOI:10.3969/j.issn.0494-0911.2005.05.008 |
| [4] |
沈蔚, 李京, 陈云浩, 等. 基于LIDAR数据的建筑轮廓线提取及规则化算法研究[J]. 遥感学报, 2008, 12(5): 692-698. |
| [5] |
周飞. 利用Alpha Shapes算法提取离散点轮廓线[J]. 湖北广播电视大学学报, 2010, 30(2): 155-156. DOI:10.3969/j.issn.1008-7427.2010.02.087 |
| [6] |
陈涛, 李光耀. 平面离散点集的边界搜索算法[J]. 计算机仿真, 2004(3): 21-23. DOI:10.3969/j.issn.1006-9348.2004.03.008 |
| [7] |
杨洋, 张永生, 马一薇, 等. 基于LiDAR数据的建筑物轮廓提取[J]. 测绘科学, 2010, 35(3): 203-205. |
| [8] |
谢建春, 姚吉利, 马宁, 等. 基于坡度梯度的点云数据中坡坎探测方法研究[J]. 测绘地理信息, 2015, 40(6): 53-56. |
| [9] |
李雯静, 李少宁, 邱佳, 等. 凸壳内缩法进行多密度离散点群边界检测[J]. 测绘科学, 2014, 39(9): 126-129. |
 2018, Vol. 43
2018, Vol. 43

