| 一种提高球形标靶点云数据质量和中心定位精度方法 |
2. 武汉大学灾害监测和防治研究中心, 湖北 武汉, 430079;
3. 武汉理工大学资源与环境工程学院, 湖北 武汉, 430070
2. Hazard Monitoring and Prevention Research Center, Wuhan University, Wuhan 430079, China;
3. School of Resource and Environment Engineering, Wuhan University of Technology, Wuhan 430070, China
作为一种非接触式的高精度测量手段,三维激光扫描技术[1]在空间信息获取、数字图书馆、医学零件精密测量等领域都有着越来越广泛的应用。该技术在短时间内可以快速获取待测物体表面的海量点云数据,但是需要在不同视角下进行多次扫描才能获得完整的点云信息,为了将不同视角下的局部点云数据拼接成完整的点云模型,需要对局部点云数据进行配准处理[2],即将不同坐标系中的局部点云转换到统一的坐标系中。
点云配准可以通过有标靶和无标靶两种形式进行。有标靶一般采用球形标靶,实际操作中使用的球形标靶大小相等,表面具有高反射性,在扫描距离、角度合适的情况下,可以获得大量球体表面点云数据,为后续球心坐标的求解过程提供了数据基础。在不同视角扫描待测物体的同时,对至少3个处于固定位置且不共线的球形标靶进行精细扫描,利用球形标靶的点云数据拟合出球心坐标,根据这些球心坐标通过四元数法或七参数法即可求解出不同视角下坐标系的转换参数,实现点云的配准。因此,在基于球形标靶的点云配准过程中,获得高精度的球形标靶中心坐标十分关键。国内外的众多学者对此也做了许多研究,不仅在最小二乘拟合算法的基础上提出了可以抵御观测值偶然误差的总体最小二乘法[3-5]和基于M估计的稳健标靶球定位算法[6],还针对扫描过程中球形标靶点云数据的系统误差提出了解决方法[7, 8]。本文针对球形标靶点云数据的特点对球形靶标中心定位的解算流程做了改进,对球形靶标的点云提取提出了基于K-邻域[9]的快速筛选方法,可以高效地获取高精度的目标点云信息,并基于整体最小二乘法对球形标靶中心坐标拟合进行K-邻域的定权改正。
1 改进的球形标靶中心定位解算方法球形标靶中心的定位精度取决于球形标靶点云数据的质量以及球面点云拟合中心坐标的解算模型和方法。
1.1 基于邻域搜索的点云提取方法球形标靶点云数据的质量直接关系到球面点中心坐标解算结果和精度,考虑到在对球形标靶进行扫描时,扫描仪所得到的原始点云数据不仅包括球形标靶点云信息,而且还包含球形标靶所在位置的点云信息以及激光在传播过程中所形成的噪声[10]点云信息,为了提取高精度的半球面点云,需要对无关点云数据进行剔除处理。由于点云数据量庞大,所以,如何快速而精准地提取出球形标靶点云是点云预处理的关键。针对上述问题,本文提出了一种改进的基于邻域搜索的点云提取方法,其基本思想是:首先,基于聚类分割的原理[11],利用原始点云的局部法向量凸性提取球形标靶的球面模型,实现原始点云的初步分离;然后,对粗处理后得到的球形标靶点云进行邻域搜索,并基于邻域点个数对点云中各离散点进行区间划分;最后,根据点云的分布特性,确定合适的点云剔除阈值,快速删除离群点,实现高精度的点云提取。
1) 点云数据初步分离。利用八叉树结构对原始点云进行分割。首先,找到点云数据在三维坐标轴上的最大值与最小值作为顶点,建立一个包含所有离散点的最小空间包围盒,该包围盒体元即对应为八叉树的根节点,它的8个顶点作为八叉树的根节点属性信息;然后,根据包围盒的体中心点以及包围盒各个面上的面中心点将包围盒继续划分为8个子包围盒,即为八叉树的子节点,并保存包围盒中的点云数据,以此类推,将这8个子节点又作为新的根节点逐渐细分。分割的准则如下:对于某一子包围盒,计算该包围盒内所有点云数据的平均法向量为:
| $ \mathit{\boldsymbol{\overline n}} = \sum\limits_{i = 0}^m {{\mathit{\boldsymbol{n}}_i}/m} $ | (1) |
式中,ni是每个离散点的单位法向量;m是该包围盒内离散点的个数。然后计算包围盒的法向量标准差[12]为:
| $ \delta = \left| {\frac{{{{\left( {\sum\limits_{i = 0}^m {{\mathit{\boldsymbol{n}}_i} - \mathit{\boldsymbol{\overline n}} } } \right)}^{1/2}}}}{m}} \right| $ | (2) |
如果δ不大于某个给定的标准差阈值T,则不再进行细分;否则细分继续进行。在细分结束之后,会得到若干个点云曲面。根据准则判断相邻两个曲面能否进行融合:
| $ \begin{array}{l} \mathit{l}{\rm{(}}{s_\mathit{i}}, {s_\mathit{j}}) = [(\mathit{\boldsymbol{n}}{}_\mathit{i}{\mathit{d}_{\mathit{ij}}} \le {\rm{||}}{\mathit{d}_{\mathit{ij}}}{\rm{||}}\cos (\frac{\pi }{2} - {\varepsilon _1})) \wedge \\ (\mathit{\boldsymbol{n}}{}_\mathit{i}{\mathit{d}_{\mathit{ij}}} \le {\rm{||}}{\mathit{d}_{\mathit{ji}}}{\rm{||}}\cos (\frac{\pi }{2} - {\varepsilon _1}))] \vee \\ (\mathit{\boldsymbol{n}}{}_\mathit{i}{\mathit{\boldsymbol{n}}_\mathit{j}} \ge 1 - {\rm{||}}{\mathit{n}_{\mathit{ij}}}{\rm{||}}\cos (\frac{\pi }{2} - {\varepsilon _2})] \end{array} $ | (3) |
式中,dij为两个曲面的中心点分别与坐标原点所组成的向量的差;ε1是控制曲面凸性程度的参数;ε2是控制点云数据中的噪声容忍程度参数[12]。当两个相邻曲面使式(3)值为真时,可以进行曲面融合。融合后替换ni和dij的值,然后重复上述步骤,直到所有曲面都参与融合过程。
2) 点云邻域搜索与分类。经过上述初步分割之后,可以将球形标靶点云与其他无关点云分离开。理想情况下球形标靶点云表面应该呈现一种近似光滑曲面的分布特征,但是点云初步分割后球形标靶点云边界处依旧存在某些离群点,并且在扫描过程中由于仪器内部的震荡及激光传播过程中产生的镜面反射都会使点云数据中出现一些异常值,这些噪声点的存在使得球形标靶点云出现不连续的表面特征。为了快速剔除点云数据中的噪声点,可以利用邻域点个数对点云数据进行分类从而实现点云数据的批量剔除。首先,设置一个距离阈值D作为邻域的搜索半径,计算散乱点云中任一点Q与其他点Qi之间的距离Di,若Di不大于阈值D,则认为点Qi是点Q的邻域点,遍历所有点之后得到点Q的邻域点个数M;然后,将所有离散点根据其邻域点的个数进行区间分类,点云中离散点的邻近点个数最小值为Tmin,最大值为Tmax,设置n个长度为k的子区间[Tmin, Tmin+k],[Tmin+k, Tmin+2k], …, [Tmin+(n-1)k, Tmin+nk],其中,Tmin+(n-1)k < Tmax < Tmin+nk, 将各个离散点根据其邻域点的个数划分不同的区间。
区间长度k的选取直接影响点云去噪的效率,k值偏小时,点云划分的区间跨度较小,而Tmin与Tmax的值是一定的,因此,子区间个数n会偏大,那么单个区间内离散点的个数也会降低,点云批量剔除的效率会大幅降低;k值偏大时,点云划分区间跨度大,单个区间内离散点个数也较多,区间批量删除离群点时会导致大量点云数据被剔除,可能会错误地删除某些非噪声点。因此,k值的确定需要根据球形标靶点云的实际数据量以及去噪的效果进行调整。
3) 点云噪声剔除。在点云的区间分类完成后,需要设置一个剔除阈值m,将[Tmin, Tmin+k]到[Tmin+(m-1)k, Tmin+mk]共m个区间内分布稀疏的离散点快速剔除掉。由于点云数据已经进行了分类处理,单次剔除的效率很高,因此,可以根据剔除效果对m值进行多次调整,直到点云数据的分布特性基本满足球面点云的分布特征,即呈现近似球形曲面分布。
1.2 基于邻域定权的球形靶标球中心坐标解算三维激光扫描系统在对球形标靶进行扫描时,在标靶球表面产生激光光斑,激光光斑的大小受到激光束入射角以及标靶球表面的特性等因素的影响,使标靶球表面点云的分布以及区域点云密度产生了差异,局部点云密度不均匀。在进行标靶球中心坐标拟合时,点云的最佳状态应该是均匀分布在球体表面,单次扫描过程中标靶球表面的离散点所占权重相同。但是经过球形标靶点云提取之后可以发现,所获得的半球状点云并不是均匀分布的。局部点云密度较大的地方相当于进行了激光扫描的重复测量,点云稀疏处各点所占的权重应该比密集处的离散点的权重更大。因此,可以利用各离散点的邻域点个数进行定权,离散点Qi的邻近点个数为Ni,点Qi的权Pi为基于Ni的函数,
球体表面方程为:
| $ {(x - {a_0})^2} + {(y - {b_0})^2} + {(z - {c_0})^2} = {r_0^2} $ | (4) |
式中,a0、b0、c0是球心坐标近似值;r是球形标靶近似半径;x、y、z是三维激光扫描系统采集的球形标靶表面点云坐标[3]。含有x、y、z的项是方程的观测值,其余项均为未知参数。运用整体最小二乘的方法,需要考虑点云观测数据的误差,因此,式(4)可以写为:
| $ \begin{array}{l} {(x + {v_x})^2} + {(y + {v_y})^2} + {(z + {v_z})^2} = \\ 2(x + {v_x})({a_0} + \delta a) + 2(y + {v_y})({b_0} + \delta b) + \\ 2(z + {v_z})({c_0} + \delta c) + {(r + \delta r)^2} - {({a_0} + \delta a)^2} - \\ {({b_0} + \delta b)^2} - {({c_0} + \delta c)^2} \end{array} $ | (5) |
表示为矩阵形式则有:
| $ \mathit{\boldsymbol{V}} = \mathit{\boldsymbol{A}}\delta \mathit{\boldsymbol{B}} - \mathit{\boldsymbol{W}} $ | (6) |
式中,
| $ \mathit{\boldsymbol{V}} = \left[ {\begin{array}{*{20}{c}} {2({x_1} - {a_0}){v_{{x_1}}} + 2({y_1} - {b_0}){v_{{y_1}}} + 2({z_1} - {c_0}){v_{{z_1}}}}\\ {2({x_2} - {a_0}){v_{{x_2}}} + 2({y_2} - {b_0}){v_{{y_2}}} + 2({z_2} - {c_0}){v_{{z_2}}}}\\ \vdots \\ {2({x_n} - {a_0}){v_{{x_n}}} + 2({y_n} - {b_0}){v_{{y_n}}} + 2({z_n} - {c_0}){v_{{z_n}}}} \end{array}} \right]; $ |
| $ \mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} {2({x_1} - {a_0})}&{2({y_1} - {b_0})}&{2({z_1} - {c_0})}&{2{r_0}}\\ {2({x_2} - {a_0})}&{2({y_2} - {b_0})}&{2({z_2} - {c_0})}&{2{r_0}}\\ \vdots &{}&{}& \vdots \\ {2({x_n} - {a_0})}&{2({y_n} - {b_0})}&{2({z_n} - {c_0})}&{2{r_0}} \end{array}} \right]; $ |
| $ \delta \mathit{\boldsymbol{B}} = \left[ {\begin{array}{*{20}{c}} {\delta a}\\ {\delta b}\\ {\delta c}\\ {\delta r} \end{array}} \right]; $ |
| $ \mathit{\boldsymbol{W}} = \left[ {\begin{array}{*{20}{c}} {x_1^2 + y_1^2 + z_1^2 - 2{x_1}{a_0} - 2{y_1}{b_0} - 2{z_1}{c_0} - (r_0^2 - a_0^2 - b_0^2 - c_0^2)}\\ {x_2^2 + y_2^2 + z_2^2 - 2{x_2}{a_0} - 2{y_2}{b_0} - 2{z_2}{c_0} - (r_0^2 - a_0^2 - b_0^2 - c_0^2)}\\ \vdots \\ {x_n^2 + y_n^2 + z_n^2 - 2{x_n}{a_0} - 2{y_n}{b_0} - 2{z_n}{c_0} - (r_0^2 - a_0^2 - b_0^2 - c_0^2)} \end{array}} \right]。$ |
根据整体最小二乘[13]的平差准则
| $ \delta \mathit{\boldsymbol{B}} = {({\mathit{\boldsymbol{A}}^\text{T}}\mathit{\boldsymbol{PA}})^{ - 1}}{\mathit{\boldsymbol{A}}^\text{T}}\mathit{\boldsymbol{PW}} $ | (7) |
其中, P=diag(Ni)。
点位中误差为:
| $ \sigma _0^2 = \sqrt {\frac{{{\mathit{\boldsymbol{v}}^T}\mathit{\boldsymbol{Pv}}}}{{n - 4}}} $ | (8) |
为了考察本文提出的算法可行性,实验采用Riegl VZ400激光扫描仪,在实验室布设4个半径均为7 cm的球形标靶。分别对球形标靶进行精细扫描,利用点云的聚类分割与快速筛选提取球形标靶的点云数据,利用最小二乘方法和基于邻域定权的最小二乘方法分别求解球形标靶中心坐标及其拟合半径,通过点位中误差以及拟合球心半径与球形标靶半径出厂值之间的比较,分析评定算法的精度。
2.1 球形标靶点云提取以球形标靶1为例,球形标靶1布设及原始点云数据如图 1所示。
 |
| 图 1 球形标靶1的布设图及原始点云数据 Fig.1 Setting Map and Raw Point Cloud of Sphere Target 1 |
首先,对点云进行初步分割,可以将球形标靶1的点云数据与无关点云分离,点云初步分割的结果如图 2所示。
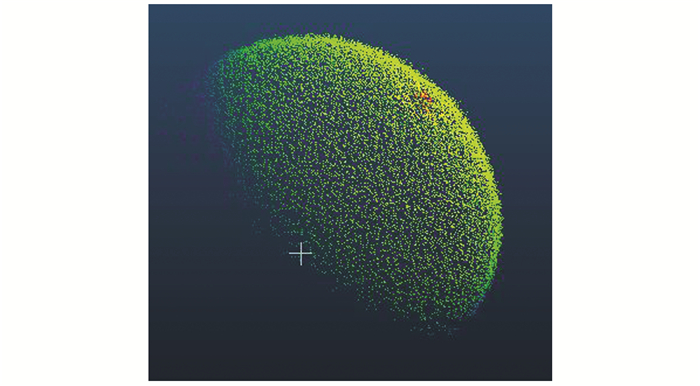 |
| 图 2 球形标靶1的点云初步分割结果 Fig.2 Initial Segmentation of Sphere Target 1 |
从图 2可以看出,经过初步分割后可以提取球形标靶的点云数据,无关的平面点云以及斜圆柱状点云已经被完全删除,只是此时球形标靶点云中依旧存在大量离群点。
然后,对初步分割的点云进行邻域搜索。为了确定合适的邻域搜索距离阈值D,分别设置距离阈值D的值为2 mm、3 mm、4 mm、…、8 mm、9 mm,对球形标靶进行邻域搜索,绘制点云中各离散点的邻域点个数分布直方图,其结果如图 3所示。
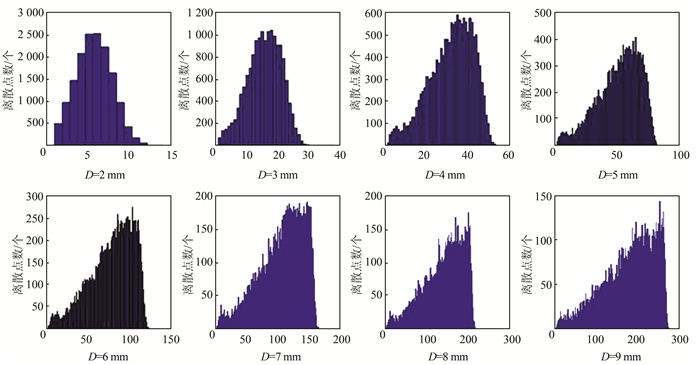 |
| 图 3 D取不同值时点云中各离散点的邻域点分布情况 Fig.3 Scatterings of Neighbors of Each Point in Point Cloud at Different Values of D |
从图 3中可以看出,距离阈值较小时,点云的区间划分失去了意义,单个区间内点云数据量过多,虽然提高了点云的剔除效率,但是会降低点云去噪的精度;而距离阈值较大时,点云的邻域搜索范围也较大,各离散点的邻域点个数趋向偏大,无法作为衡量离散点是否为离群点的指标。依图 3所示,为了保证点云数据去噪的速率与效果,距离阈值的选取在4~6 mm较为适宜,因此,选取5 mm作为距离阈值进行标靶球点云的邻域搜索。
通过计算得到球形标靶点云中各离散点的邻近点个数,其点云离散点的邻近点个数分布在区间[0, 85]内,通过多次试验,以5作为划分长度,将点云中各离散点划分为17个区间,将区间1~6内的离散点批量剔除,剔除结果如图 4所示。
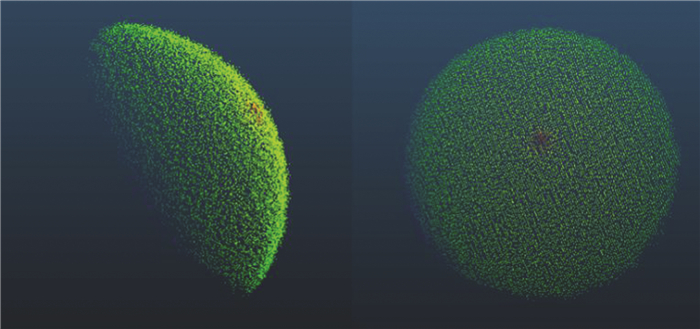 |
| 图 4 球形标靶1的点云提取结果 Fig.4 Point Cloud Obtainment of Sphere Target 1 |
从图 4中可以看出,经过基于区间分类的点云噪声点剔除处理之后,球面点云中分布较为稀疏的离群点被删除。利用同样方法,对其余3个球形标靶点云数据进行处理,最终得到球形标靶点云数据提取结果如表 1所示。
| 表 1 球形标靶点云数据提取结果 Tab.1 Point Cloud Obtainment of 4 Sphere Targets |
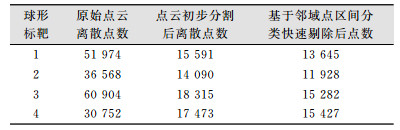 |
从表 1可以看出,球形标靶球原始点云数据量十分庞大,点云的初步分割可以提取出球形标靶的球面点云数据。通过基于邻域搜索的点云分类方法可以快速剔除球形标靶中的离群点,得到精度较高的球形标靶点云数据,同时由于区间分类体现了点云分布的直观性,在进行点云剔除时也可以保证剩余点云数据的充足性。
2.2 球形标靶中心定位分别利用整体最小二乘法以及基于邻域点个数定权的整体最小二乘法对4个标靶球点云进行中心坐标拟合,结果如表 2所示。
| 表 2 球形标靶中心坐标解算结果/m Tab.2 Coordinates of Sphere Target Centers/m |
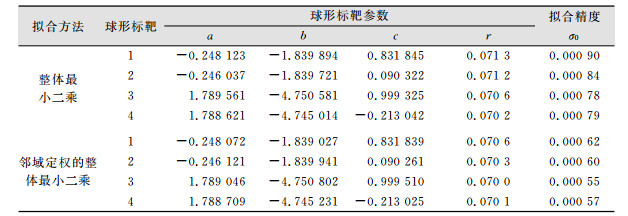 |
由表 2可以看出,利用整体最小二乘法可以得到较高精度的球形标靶中心坐标,在经过基于邻域点个数的加权改正之后,所求得的标靶球中心坐标的精度有了进一步的提高。加权改正之后球形标靶中心坐标的点位中误差平均减小了29%;整体最小二乘所拟合得到的球形标靶半径与真实值最大相差1.3 mm,而基于邻域定权的整体最小二乘拟合得到的半径与真实值相差0.6 mm,由此可以看出,利用邻域点个数进行定权的解算方法可以提高球形标靶的定位精度。
3 结束语本文针对有标靶的点云配准问题,提出了球形标靶点云数据处理的改进算法流程。在点云数据预处理过程中,基于点云的聚类分割提出了离散点邻域区间分类的点云快速提取方法,实现球形标靶点云离群点的高效剔除,保证了参与后续处理的数据的准确性。同时对标靶球中心坐标的解算方法提出了基于邻域点个数的定权改进。从实验结果来看,本文的算法得到的球形标靶中心坐标的精度有所提高,有助于提升有标靶的点云配准的精度。
| [1] |
徐源强, 高井祥, 王坚. 三维激光扫描技术[J]. 测绘信息与工程, 2010, 35(4): 5-6. |
| [2] |
李彩林, 郭宝云, 季铮. 多视角三维激光点云全局优化整体配准算法[J]. 测绘学报, 2015, 4(2): 183-189. |
| [3] |
鲁铁定, 周世健, 张立亭, 等. 基于整体最小二乘的地面激光扫描标靶球定位方法[J]. 大地测量与地球动力学, 2009, 29(4): 102-105. |
| [4] |
鲁铁定, 周世健. 总体最小二乘的迭代解法[J]. 武汉大学学报·信息科学版, 2010, 35(11): 1 352-1354. |
| [5] |
袁豹, 岳东杰, 赵元忆, 等. 基于稳健加权总体最小二乘法的地面三维激光扫描球型标靶定位[J]. 勘察科学技术, 2013(1): 19-22. DOI:10.3969/j.issn.1001-3946.2013.01.005 |
| [6] |
官云兰, 詹新武, 程效军, 等. 一种稳健的地面激光扫描标靶球定位方法[J]. 工程勘察, 2008(10): 42-45. |
| [7] |
张毅, 闫利, 杨红, 等. 地面激光扫描球形标靶的球心误差研究[J]. 武汉大学学报·信息科学版, 2012, 37(5): 598-601. |
| [8] |
蔡建民, 花向红, 宣伟, 等. 地面三维激光扫描仪系统误差模型研究及精度分析[J]. 测绘地理信息, 2016, 41(5): 17-21. |
| [9] |
张毅, 刘旭敏, 隋颖, 等. 基于K-近邻点云去噪算法的研究与改进[J]. 计算机应用, 2009, 29(4): 1 011-1014. |
| [10] |
王振, 孙志刚. 散乱点云噪声分析与降噪方法研究[J]. 计算机与数字工程, 2015, 43(9): 1668-1673. DOI:10.3969/j.issn1672-9722.2015.09.028 |
| [11] |
吴世雄, 王成勇. 散乱噪声点云的数据分割[J]. 机械工程学报, 2007, 43(2): 230-233. DOI:10.3321/j.issn:0577-6686.2007.02.040 |
| [12] |
傅欢, 梁力, 王飞, 等. 采用局部凸性和八叉树的点云分割算法[J]. 西安交通大学学报, 2012, 46(10): 60-65. |
| [13] |
鲁铁定, 陶本藻, 周世健. 基于整体最小二乘法的线性回归建模和解法[J]. 武汉大学学报·信息科学版, 2008, 33(5): 504-507. |
 2018, Vol. 43
2018, Vol. 43


