2013年起，IGS(International GNSS Service)实时工作组开始提供实时的精密钟差轨道差分服务，其分析中心的GPS实时轨道精度在5 cm左右，钟差精度在0.3 ns左右，更新频率为5 s^[1]。赵齐乐等^[2]利用非差观测量和最终轨道估计GPS/北斗钟差，精度优于0.15 ns。由于在非差模式下，估计器中存在大量的模糊度参数，矩阵的维数制约了解算的速度，文献[3]通过对矩阵运算进行优化，提高解算效率。文献[4-8]提出利用非差和历元差分双线程的方法估计卫星钟差，钟差更新频率优于1 Hz。

本文采用一种双线程钟差加密的方法，能有效提高解算效率，同时保留了非差解算的精度。选用超快速预报轨道和76个全球均匀分布的参考站，基于双线程钟差加密算法对四系统的卫星钟差进行事后仿实时估计，并从轨道精度，解算效率，钟差精度和最终定位结果等方面对该实时系统进行分析和评估。

GNSS(global navigation satellite system)无电离层组合非差钟差估计的数学模型如下：

式中，r代表测站号; s代表卫星号; P_r^s和L_r^s代表GNSS伪距和相位的无电离层观测值，单位为m; ρ_r^s为测站与卫星端的几何距离; c为光速; dt_r为接收机钟差; dt^s为卫星钟差; T_r为对流层延迟; B_r^s和B^s代表接收机和卫星端的伪距硬件延迟; e_r^s代表测站r伪距的观测噪声; λ^s为无电离层组合波长; N_r^s为无电离层组合模糊度; b_s^r和b^s分别为接收机和卫星端相位硬件延迟; ε_r^s为测站r相位的观测噪声。

在进行钟差估计时，由于测站坐标静止不动且已知，可以将其固定，减少参数的个数。选取接收机钟差、卫星钟差、对流层和模糊度作为待估参数^[9-11]。为了消除系统间偏差的影响，同时估计了一个接收机钟差和多个系统间偏差。对于CDMA(code division multiple access)系统而言，参数B_r^s与卫星s无关。因此在参数估计时，可以被吸收进接收机钟差当中; 对于FDMA(frequency division multiple access)系统而言，由于不同卫星的信号频率不同，硬件延迟也不同，考虑到估计器的维数限制，不将其作为待估参数，认为其公共部分被吸收进接收机钟差，各卫星不符值被吸收进伪距残差; B^s为卫星端的伪距硬件延迟，由于其与卫星钟差不可分离，在参数估计时被吸收进卫星钟差中。经过上述的参数重整，各参数的实际估值变为:

式中，$ \bar{B}_{r}$代表接收机r对同一系统卫星的伪距硬件延迟的公共部分。在实时GNSS的应用中，对数据更新的速度要求很高，对于大规模参考网来说，参数的个数限制了钟差解算的速度。在实时钟差解算中，假设GNSS处理了m个测站，k颗卫星，共s个导航系统, 则观测值的个数n和参数的个数p满足下列关系式：

其中参数p具体包括：①与测站相关的接收机钟差(s)和对流层参数; ②与卫星相关的卫星钟差(t); ③与传播路径相关的模糊度参数$ \sum\limits_{i=1}^{m} k_{i}$。从式(4)中可以看出，滤波器中的参数大部分为模糊度参数，且与测站数目成正比。为减少算法耗时，采用双线程加密的算法进行处理。主线程为非差线程，采样率可设置为5 s，估计接收机钟差、对流层、卫星钟差和模糊度参数; 辅线程为加密线程，采样可设置为1 s，估计接收机钟差、对流层和卫星钟差参数，模糊度参数固定为非差线程所估计的模糊度。由于模糊度参数存在收敛的过程。因此只选用收敛之后的模糊度参数，默认收敛时间为20 min。从上述分析中可知，实时系统初始化所需时间为20 min，20 min之后，即可提供1 s采样率的高精度实时钟差。

由于GNSS观测量是测站和卫星之间的相对时间延迟，若将参考网中所有接收机端和卫星端的钟差作为待估参数，将会出现秩亏，因此必须设置钟差参考基准，此时所估计出来的钟差为相对于参考基准的相对钟差。研究表明，在基准钟的钟差优于10~6 s时，该基准与实际时间的差异可被接收机钟差吸收，对定位无影响^[12]。本文选取的是卫星钟差改正量的重心基准。

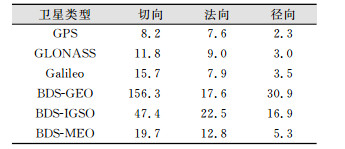
为了具体验证本文算法的可行性，选取2018年年积日为006~007全球共76个测站的观测数据进行钟差解算试验，数据采样间隔为30 s，利用事后仿实时的模式解算卫星钟差，为了区分非差线程和加密线程，设置非差线程采样率为300 s，加密线程的采样率为30 s。轨道固定为武汉大学提供的6 h超快速轨道，该轨道文件包含了48 h的GPS/BDS/ GLO/GAL四系统轨道，前24 h为实测轨道，后24 h为预报轨道。考虑到轨道发布需要延迟2 h，在钟差估计时，使用的是每个文件第2~8 h的预报轨道，其轨道精度统计值如表 1所示。从表中可以看出GPS预报轨道径向方向精度最好，为2.3 cm，GLONASS和Galileo轨道精度相当，为3 cm左右，北斗预报轨道精度与卫星类型有关，GEO卫星精度最差，IGSO次之，MEO卫星精度最好。

表 1(Tab.1)

表 1 预报轨道精度统计表/cm Tab.1 The RMS Values of Predicted Orbit/cm

表 1 预报轨道精度统计表/cm Tab.1 The RMS Values of Predicted Orbit/cm 卫星类型 切向 法向 径向 GPS 8.2 7.6 2.3 GLONASS 11.8 9.0 3.0 Galileo 15.7 7.9 3.5 BDS-GEO 156.3 17.6 30.9 BDS-IGSO 47.4 22.5 16.9 BDS-MEO 19.7 12.8 5.3

以上述钟差解算为例，对于非差线程来说，平均每个历元所估计的参数约为2 300个，矩阵维数制约了求解的效率; 对于加密线程来说，由于不考虑模糊度参数，参数的个数下降为480个左右，极大地提高了矩阵操作的速度。为减少非差线程的耗时，采用均方根滤波进行滤波估计，用QR(正交三角)分解避免了求逆的过程^{[13, 14]}，同时选取LAPACK数学库进行相关的矩阵运算，加快算法的解算速度，以满足非差线程5 s更新的要求。将上述试验中年积日为007的解算耗时绘制如图 1所示。从图 1中可以看出，每个历元的耗时都非常稳定，非差线程的平均耗时为1.483 s，加密线程的平均耗时为0.247 s，钟差更新频率优于1 Hz。

图 1(Fig.1)

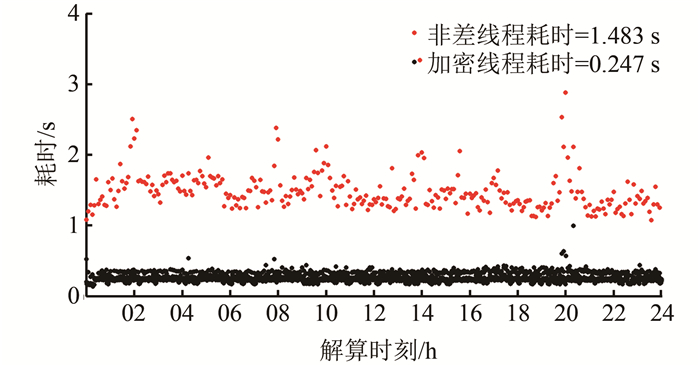图 1 非差和加密线程耗时统计图 Fig.1 Time-Consuming Series of the Undifferenced Thread and Interpolation Thread

为了有效评估解算钟差的精度，本文采用改进的二次差方法进行比较^[15]，其公式如下:

式中，$\delta {t^s}(i)、\delta t_0^s(i) $表示第i个历元解算钟差和最终钟差; B(i)第i个历元两套钟差的基准差异。在估计钟差和最终钟差之间做一次差，并将该一次差的平均值作为两套钟差的基准差异，并从一次差中扣除，这样避免了基准钟异常时影响评估结果的情况。以武汉大学提供的30 s采样间隔的最终钟差产品Whs作为参考，其事后产品已与IGS(International GNSS Service)及其他分析中心的精度相当^[16]，可以将其作为真值进行钟差评估。利用改进的二次差法，统计加密线程所解算的钟差与最终产品的差异，并将统计值绘制如下。由于卫星轨道径向误差和卫星钟差具有耦合性，在钟差估计时，钟差能吸收90%的轨道径向误差^[17]。因此解算钟差和Whs最终钟差并不是完全吻合。从图 2可以看出, GPS卫星钟差精度大部分在0.2 ns以下，其中G21号卫星偏差最大，是因为G21卫星的轨道误差偏大。从图 3可以看出，GLONASS卫星的钟差精度在0.2~0.4 ns左右。从图 4可以看出，北斗GEO卫星钟差精度偏大，在0.6~1.0 ns左右，IGSO次之，在0.5 ns左右，MEO精度最好，在0.3 ns左右，其变化与轨道一致; Galileo卫星精度在0.2~0.3 ns左右。

图 2(Fig.2)

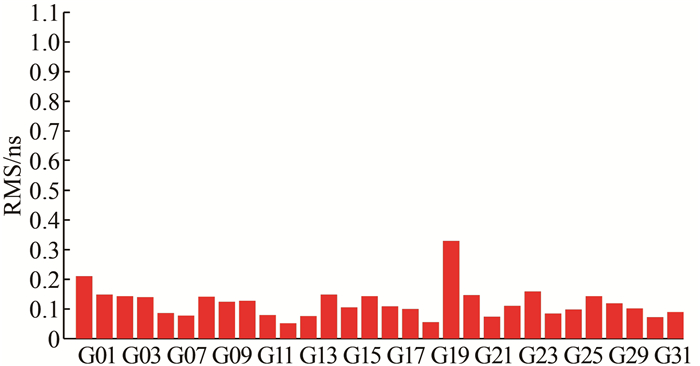图 2 GPS卫星钟差统计图 Fig.2 Average RMS of GPS Satellites Clock Compared to the Whs

图 3(Fig.3)

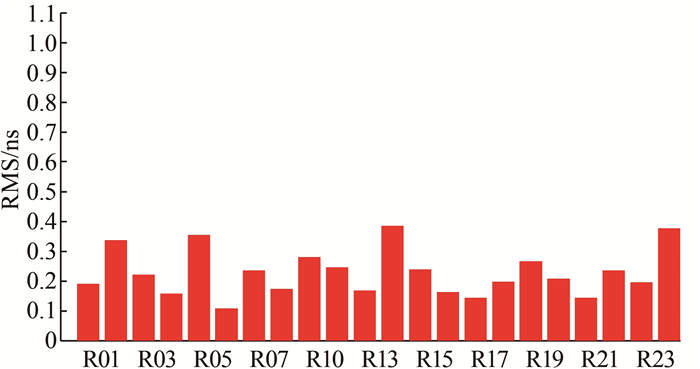图 3 GLONASS卫星钟差统计图 Fig.3 The Average RMS of GLONASS Satellites Clock Compared to the Whs

图 4(Fig.4)

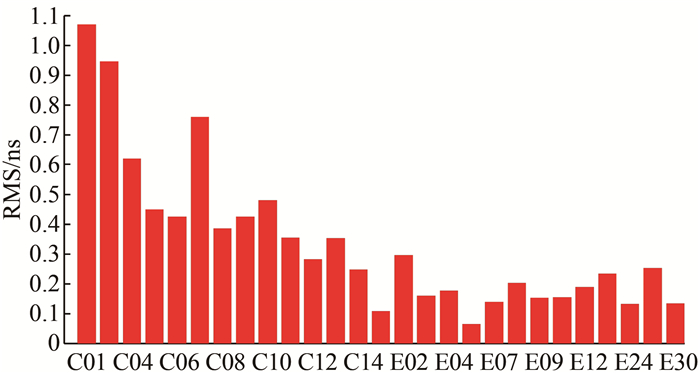图 4 北斗和Galileo卫星钟差统计图 Fig.4 The Average RMS of BDS and Galileo Satellites Clock Compared to the Whs

为了验证解算钟差的定位性能，以MGEX网ALIC测站为例，采用加密线程解算的钟差进行动态精密单点定位。由于钟差吸收了部分轨道误差，因此所采用的轨道应和解算钟差时保持一致。设计GPS、GPS+GLO、GPS+GAL、GPS+BDS、GPS+GLO+GAL、GPS+GLON+GAL+BDS共6种不同的定位模式，分析多系统融合对精密单点定位的影响。图 5绘制了其解算坐标与参考值的差异在E、N、U(东、北、高)3个方向的定位序列图。其中横轴表示时间，解算时刻; 纵轴是解算坐标与参考值的差异。

图 5(Fig.5)

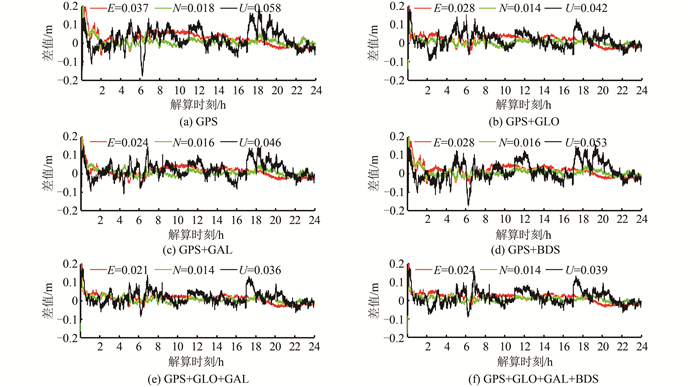图 5 ALIC测站不同定位模式定位时序图 Fig.5 The Series of ALIC Station Using Different Positioning Mode

在单GPS模式下，GPS平均观测卫星数为9.4颗，平面精度E方向精度为3.7 cm，N方向精度为1.8 cm, 高程精度为5.8 cm，在分别加入GLO、GAL、BDS导航系统之后，观测卫星数平均增加了6.5颗、3.2颗和4.1颗, 对定位精度分别有一定提高，其中以加入GLO导航系统对精度的提高最大，E方向精度提高至2.8 cm，N方向精度提高至1.4 cm，U方向提高至4.2 cm。在不断加入其他导航系统后，收敛时间也得到了提高，以平面精度收敛至10 cm，高程收敛至20 cm为界限，收敛时间从单GPS的35 min缩短至四系统融合时的15 min，收敛时间缩短了57%。

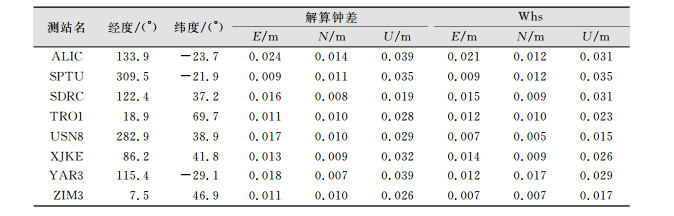
为了评估解算钟差与事后钟差定位性能的差异，选取全球均匀分布且未参与钟差解算的8个多系统测站进行GPS、GLONASS、Galileo、BDS四系统融合精密单点定位，且与Whs最终钟差解算的结果进行对比，统计其收敛之后的定位结果。从表 2中可以看出，采用解算钟差和Whs事后钟差定位性能相当，平面精度均在3 cm以下，高程精度在5 cm以下。

表 2(Tab.2)

表 2 采用解算钟差和事后钟差定位结果表 Tab.2 The PPP Results Using Satellites Clock Estimated in this Article Compared to Whs

表 2 采用解算钟差和事后钟差定位结果表 Tab.2 The PPP Results Using Satellites Clock Estimated in this Article Compared to Whs 测站名 经度/(°) 纬度/(°) 解算钟差 Whs E/m N/m U/m E/m N/m U/m ALIC 133.9 -23.7 0.024 0.014 0.039 0.021 0.012 0.031 SPTU 309.5 -21.9 0.009 0.011 0.035 0.009 0.012 0.035 SDRC 122.4 37.2 0.016 0.008 0.019 0.015 0.009 0.031 TRO1 18.9 69.7 0.011 0.010 0.028 0.012 0.010 0.023 USN8 282.9 38.9 0.017 0.010 0.029 0.007 0.005 0.015 XJKE 86.2 41.8 0.013 0.009 0.032 0.014 0.009 0.026 YAR3 115.4 -29.1 0.018 0.007 0.039 0.012 0.017 0.029 ZIM3 7.5 46.9 0.011 0.010 0.026 0.007 0.007 0.017

本文基于Whu预报轨道，选取全球均匀分布的76个参考站，利用双线程钟差加密算法和均方根滤波实现对四系统钟差的实时估计，非差线程耗时优于2 s，加密线程耗时优于0.5 s。钟差统计结果表明，GPS实时钟差精度优于0.2 ns，GLONASS钟差精度优于0.4 ns，Galileo钟差精度优于0.3 ns，受轨道影响，北斗GEO实时钟差精度为0.6~1.0 ns，IGSO钟差精度在为0.4~0.7 ns，MEO钟差精度为0.3~0.4 ns。基于解算钟差进行PPP动态试验，多模融合定位有助于缩短PPP收敛时间，提高定位精度^{[18, 19]}，且定位精度与事后钟差定位结果相当，平面精度在3 cm以下，高程精度在5 cm以下。采用非差观测量进行钟差估计时，滤波器中保留了大量的模糊度参数，本文利用模糊度参数进行钟差加密实现了卫星钟差秒级更新，后续也可利用该模糊度参数提取卫星的非整数相位偏差，为之后的模糊度固定^[20]提供一些有益的帮助。