| 稳健估计方法在点云圆柱拟合中的应用 |
与传统的全站仪测量相比,三维激光扫描技术的高效、快捷、精确、方便等优点,使其在城市三维建模、矿山地质测绘、变形监测和古迹测量等领域具有广泛的应用[1]。在工业测量中,需要根据实际情况拟合各种圆柱形物体,进行圆柱拟合的目的就是计算得到圆柱的圆心坐标、方向和半径[2]。
目前,常用的圆柱拟合方法中:高斯图法、遗传算法和特征值法这3种方法的理论模型较为复杂,不易理解和实现,由于参数之间的相关性,需要选取较为准确的初值且不具备抗差性;几何特性法、圆度判别法和坐标转换法这3种方法较容易理解和实现,但是对初值也有较强的依赖性,同时也不具备抗差性[3-5]。文献[6]通过变换基于坐标转换的误差方程来降低参数之间的相关性。文献[7]主要利用三倍中误差探测法剔除粗差后实现了坐标转换法拟合圆柱。文献[8]主要介绍了再生权最小二乘法(self⁃ born weighted least squares,SBWLS)和其他稳健估计方法的对比分析。本文将介绍一种有效可行的圆柱拟合方法,该方法基于坐标转换拟合法和再生权最小二乘稳健估计法,在降低参数对初值选取的要求的同时,也不用对观测值进行粗差剔除处理,还可以拟合任意倾斜角度的圆柱。
1 拟合模型与参数估计方法 1.1 坐标转换拟合法获取初值为了便于求解圆柱的几何参数,以圆柱中心轴线与测量坐标系XOY平面的交点为坐标原点,圆柱中轴线为Z轴,建立圆柱标准坐标系,将测量坐标系X通过坐标转换到标准坐标系Y[4]:
| $ \boldsymbol{X}=\boldsymbol{X}_{0}+\boldsymbol{R Y} $ | (1) |
| $ \boldsymbol Y=\boldsymbol R^{\mathrm{T}}\left(\boldsymbol{X}-\boldsymbol{X}_{0}\right) $ | (2) |
式中,
标准坐标系中圆柱面可表示为:
| $ x^{2}+y^{2}=r^{2} $ | (3) |
得到以测量点到圆柱表面的距离为残差的误差方程:
| $ v_{i}=\sqrt{x^{2}+y^{2}}-r $ | (4) |
式中,x和y是标准坐标系中的点坐标;r为圆柱半径。
将误差方程转换为矩阵的形式
| $ v_{i}=\sqrt{\left(\boldsymbol X_{i}-\boldsymbol X_{0}\right)^{\mathrm{T}} \boldsymbol R \boldsymbol{\varLambda} \boldsymbol R^{\mathrm{T}}\left(\boldsymbol X_{i}-\boldsymbol X_{0}\right)}-r $ | (5) |
式中,
将误差方程线性化,由于存在根式,导致各参数之间的相关性很强,所以线性化过程中所舍弃的二次项不可忽略,因此需要较为准确的初值,若参数初值与真值偏差较大,在参数求解时很难拿收敛到正确的值,从而得不到正确的结果[3]。
为了降低各参数之间相关性,对误差方程进行变换。令误差方程为:
| $ v_{i}=x^{2}+y^{2}-r^{2} $ | (6) |
将误差方程转换为矩阵的形式:
| $ v_{i}=\left(\boldsymbol{X}_{i}-\boldsymbol{X}_{0}\right)^{\mathrm{T}} \boldsymbol{R} \boldsymbol{\varLambda} \boldsymbol{R}^{\mathrm{T}}\left(\boldsymbol{X}_{i}-\boldsymbol{X}_{0}\right)-r^{2} $ | (7) |
与误差方程式(4)相比,方程式(6)中没有根式,故参数之间的相关性大大降低,这样线性化过程中的二次项就可以舍去,降低了对参数初值选取的要求,避免参数求解错误。
根据间接平差迭代求取参数估值,但是该方法不是以圆度平方和最小为准则[7],得到的结果并不是参数的最佳估值。但此时参数估值已经较为准确,可以将其作为参数初值按式(5)的误差方程再次迭代求解,从而得到参数的最佳估值。可由式(3)得到圆柱面方程,由式(5)得到的残差值即为圆柱的圆度值。
1.2 再生权最小二乘稳健估计法统计学家指出,观测值中出现粗差的概率大概为1%~10%,这些粗差会降低参数估计的精度,因此,在参数估计的过程中,需要消除或减弱粗差对参数估计的影响。目前,对含粗差观测值的处理方法主要有两种,第一种是将含粗差观测值视为期望异常,用统计检验法剔除含粗差的观测值之后再进行参数估计;第二种是将含粗差观测值视为方差异常,采用稳健估计方法对其进行处理[8]。通过三维激光扫描获取的点云数据中,包含了很多异常数据,根据点云数据对圆柱进行拟合时,在不进行粗差剔除的情况下拟合得到较为精确的圆柱参数。本文采用了稳健估计方法中的SBWLS来解决这个问题。
SBWLS是一种有效可行的稳健估计方法。它充分利用观测值的改正数(残差)条件方程提供的有效信息,用观测值改正数的多个估值来构造观测值的权,而不是直接用最小二乘法(least squares,LS)得到的观测值改正数来计算观测值的权。实验证明,与其他常用的稳健估计方法相比,SBWLS法能更有效地消除或减弱粗差对参数估计的影响[8]。
列出误差方程:
| $ \boldsymbol V=\boldsymbol B \hat{\boldsymbol x}-\boldsymbol l \text {, 权为 } \boldsymbol P $ | (8) |
式中,
用最小二乘法求得参数改正数
将式(8) 中的系数矩阵
| $ \boldsymbol V_{t}=\boldsymbol B_{t} \hat{\boldsymbol x}-\boldsymbol l_{t} $ | (9) |
| $ \boldsymbol V_{r}=\boldsymbol B_{r} \hat{\boldsymbol x}-\boldsymbol l_{r} $ | (10) |
由式 (9) 可得
| $ \hat{\boldsymbol x}=\boldsymbol B_{t}^{-1}\left(\boldsymbol V_{t}+\boldsymbol l_{t}\right) $ | (11) |
| $ \boldsymbol V_{r}=\boldsymbol B_{r t} \boldsymbol V_{t}-\boldsymbol W_{r t} $ | (12) |
式中,
根据偶然误差的特性, 可用
| $ \boldsymbol V^{(i)} =\left[v_{1}^{(i)} v_{2}^{(i)} \cdots v_{n}^{(i)}\right]^{\mathrm{T}}, i=1, 2, \cdots, m $ | (13) |
| $ \left|v_{j}^{(i)}\right| \leqslant \frac{\eta \hat{\sigma}_{0}}{\sqrt{p_{j}}}, i=1, 2, \cdots, m ; j=1, 2, \cdots, n $ | (14) |
式中, 当
用同一个观测值改正数(残差)的多个估值,由多个估值计算观测值的再生方差,根据再生方差计算得到观测值的再生权[9-11]。其计算公式为:
| $ \dot{\sigma}_{j}^{2}=\frac{1}{m} \sum\limits_{i=1}^{m}\left(v_{j}^{(i)}\right)^{2}, j=1, 2, \cdots, n $ | (15) |
| $ \bar{\sigma}_{0}^{2}=\frac{1}{n} \sum\limits_{j=1}^{n} \dot{\sigma}_{j}^{2} $ | (16) |
| $ \dot{p}_{j}=\frac{\bar{\sigma}_{0}^{2}}{\dot{\sigma}_{j}^{2}}, j=1, 2, \cdots, n $ | (17) |
将计算得到的再生权作为观测值的权,按LS法迭代求解参数估值的方法称为SBWLS9]。
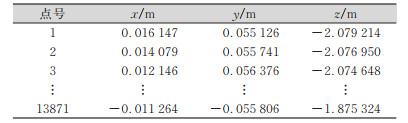
2 圆柱拟合计算实例 2.1 数据准备扫描了某圆柱形物体,得到如表 1所示的点云数据(人为的加入了一些粗差点)。点云三维散点图如图 1所示,图 1中散布于集中点云周围的点,即为粗差点。
| 表 1 点云坐标数据 Tab.1 Point Cloud Data |
 |
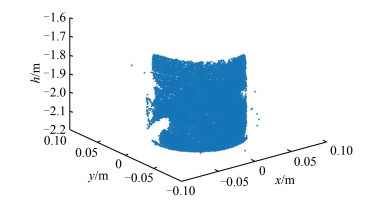 |
| 图 1 点云数据散点图 Fig.1 Coordinate 3D Scatter Images |
2.2 圆柱拟合
基于上述方法拟合此点云柱面参数,将五参数初值设置为x0=0,y0=0,α=0,β=0,r=1。首先,使用初值任意选取的方法迭代求取参数,将此作为初值,分别使用LS(不抗差)和SBWLS(抗差)进行参数估计,比较分析两种方法的平差结果。
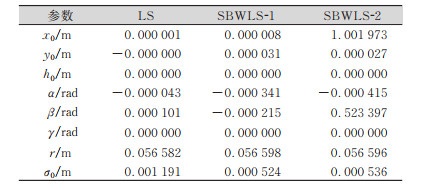
从表 2(表中参数含义见§1.1)可以得出,LS和SBWLS-1两种方法平差参数结果接近,SBWLS-1法平差的单位权中误差小于LS法,证明了SBWLS法的抗差性。图 2为圆柱拟合结果图。
| 表 2 平差结果对比 Tab.2 Comparison of Adjustment Results |
 |
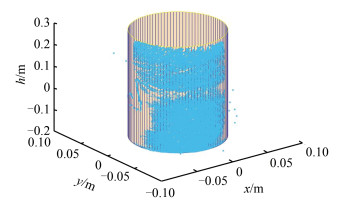 |
| 图 2 圆柱三维拟合图 Fig.2 Cylinder 3D Fitting Images |
为了验证该方法的通用性,将表 1中的点云数据进行一定数值的坐标平移和旋转变换,然后按照SBWLS法求解圆柱面参数,由表 2中的SBWLS-2可得出,拟合结果中圆柱的半径r不变,说明该方法能成功拟合各种情况下的圆柱。
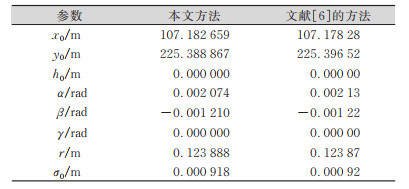
为了进一步验证该方法的正确性,本文采用文献[6]中的实例数据(不含粗差),用SBWLS法的拟合结果与文献[6]的拟合结果进行比较。如表 3所示(表中参数含义见§1.1),可得出两种方法的拟合结果基本一致,拟合精度也相当。
| 表 3 两种方法结果对比 Tab.3 Comparison of Results of Two Methods |
 |
2.3 拟合结果评定
一般可以用中误差、残差、残差分布特性等来评定圆柱面拟合结果[6]。SBWLS法计算得到的单位权中误差为0. 524 mm,与采集点云数据仪器的精度相吻合,说明此方法的拟合结果良好。另外,通过对计算结果进行统计分析,绘制残差的折线图和分布图,如图 3(a)和图 4(a)所示,发现粗差点的残差非常大。对非粗差点的残差进行局部放大,如图 3(b)和图 4(b)所示,发现其分布呈现随机性和正态性,符合偶然误差的几大特性。由此可以得出SBWLS法的拟合结果具有较高可靠性。
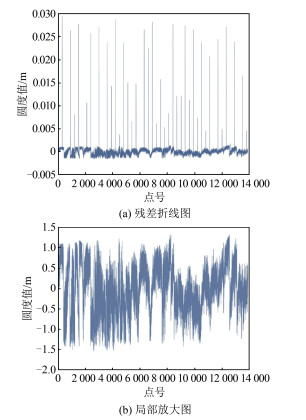 |
| 图 3 残差(圆度)折线图 Fig.3 Residual Line Images |
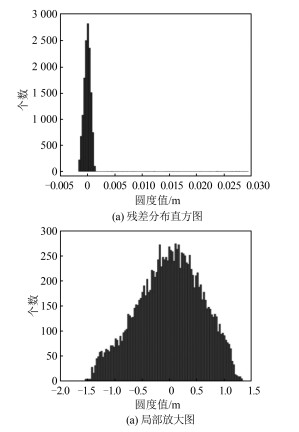 |
| 图 4 残差(圆度)分布图 Fig.4 Residual Plot Images |
3 结束语
在圆柱拟合的实际工程应用中,很多情况下无法知道圆柱参数的近似值,导致误差方程结构不够理想,同时观测值中不可避免的存在一些粗差,因此仅仅依靠最小二乘法求解出正确的圆柱参数就比较困难。本文方法无需顾及初值选取、粗差探测。通过对含有粗差的不同方向的点云数据进行拟合,发现能够有效地消除或减弱粗差对参数估计的影响;通过与其他圆柱面拟合的方法比较,发现该方法所求解的圆柱参数结果和精度符合实际,适用于各种情况下的圆柱拟合;通过进一步对参数结果进行统计分析,发现圆度的分布随机且符合正态特性,验证了该方法的正确性。
| [1] |
索俊锋, 刘勇, 蒋志勇, 等. 基于三维激光扫描点云数据的古建筑建模[J]. 测绘科学, 2017, 42(3): 179-185. |
| [2] |
卢小平, 朱宁宁, 禄丰年. 基于椭圆柱面模型的隧道点云滤波方法[J]. 武汉大学学报·信息科学版, 2016, 41(11): 1476-1482. |
| [3] |
田晓, 李全海. 基于坐标转换的三维空间圆柱面拟合[J]. 工程勘察, 2014, 42(12): 79-82. |
| [4] |
任营营, 王解先. 无需顾及初值的坐标转换法拟合任意方向点云圆柱面[J]. 矿山测量, 2018, 46(6): 105-109. |
| [5] |
严宇, 王解先. 激光扫描点云数据的圆柱拟合方法[J]. 测绘科学, 2018, 43(6): 83-87. |
| [6] |
张益泽, 王解先. 初值任意选取的圆柱面拟合方法[J]. 工程勘察, 2012, 40(1): 77-80. |
| [7] |
葛永慧. 再生权最小二乘法研究[J]. 测绘通报, 2014(8): 36-39. |
| [8] |
王解先, 季凯敏. 工业测量拟合[M]. 北京: 测绘出版社, 2008: 91-100.
|
| [9] |
袁媛. 基于再生权最小二乘法的坐标系统转换参数优化[D]. 太原: 太原理工大学, 2013
|
| [10] |
史翔, 赵超英, 刘万科. 空间直线拟合的加权极坐标法[J]. 测绘地理信息, 2019, 44(2): 120-123. |
| [11] |
王乐洋, 温贵森. 相关观测PEIV模型的最小二乘方差分量估计[J]. 测绘地理信息, 2018, 43(1): 8-14. |
 2022, Vol. 47
2022, Vol. 47

