| 顾及空间信息与全卷积神经网络的高分辨率遥感影像分类方法 | [PDF全文] |
随着对地观测技术的不断发展,遥感影像的空间分辨率不断提高。地物在高分辨率遥感影像上呈现出更为丰富的细节,影像信息量的增加和地表覆盖构成的复杂化给影像解译带来了巨大的挑战[1]。高分辨率遥感影像分类作为遥感影像解译的关键问题之一,已受到国内外学者的广泛关注。
目前,高分辨率遥感影像分类方法大体可分为非监督分类和监督分类两大类。相比K均值聚类、模糊C均值聚类(fuzzy C-means, FCM)、ISODATA算法等非监督分类方法[2-4],监督分类方法由于使用了先验知识,通过先训练再分类,往往能获得较高的分类精度。现有的监督分类方法主要包括K近邻(K-nearest neighbor, KNN)[5]、支持向量机(support vector machine, SVM)[6]等,其通过从影像中人工选取颜色、纹理、形状等底层特征,增加训练集的多样性,提升分类器的泛化能力,从而获得更优的分类结果。然而,影像空间分辨率的提高使得同类地物的特征相似性减少、不同类地物的特征相似性增大。此时,无论是使用单一特征还是多元特征,影像的底层特征和上层理解之间总是存在着较大的差异,导致人工选取的底层特征难以满足实际高分辨率遥感影像地物分类的需求。
深度学习方法[7-9]作为传统神经网络方法的发展,为高分辨率遥感影像分类提供了新的思路。卷积神经网络(convolutional neural networks, CNN)[10]作为一种带有卷积结构的深度学习方法,通过多层神经元的自我学习机制可以从输入数据中获得大量由底层到高层的特征信息,避免了传统影像分类方法人工选取特征的局限性。Lagrange等[11]针对高分辨率遥感影像分类,将CNN方法与SVM等其他传统分类方法进行对比,实验结果证明了CNN方法的有效性。Penatti等[12]采用多个CNN叠加的方法进行高分辨率遥感影像分类,在UCMerced数据集上取得了较高的分类精度。然而,CNN中池化层与全连接层的存在使得网络后半部分空间信息缺失,难以做到像素水平的分类。为此,Long等[13]在2015年提出了全卷积神经网络(fully convolutional networks, FCN)方法,通过对CNN网络进行结构性改进,实现了像素水平的影像分类。Marmanis等[14]将FCN方法运用到高分辨率遥感影像分类中,提高了影像的全局分类精度。Maggiori等[15]采用FCN方法进行高分辨率遥感影像的建筑物识别,取得了良好的识别效果。Fu等[16]使用改进的FCN方法进行高分辨率遥感影像分类,通过带孔卷积等操作进一步提升了分类效果。然而,由于FCN中神经元的感受域过大,且缺少空间信息约束,一般难以得到边缘平滑的分类结果。条件随机场(conditional random fields, CRF)作为一种概率图模型,通过引入上下文信息进行空间特征约束,能够平滑类别边缘,减少噪声。文献[17-18]分别将CRF同SVM和FCM结合用于遥感影像分类,实验结果表明CRF方法可以进一步提高影像分类的精度。因此,本文将CRF与FCN结合,弥补FCN缺少空间信息约束的不足,取得了令人满意的分类精度。
基于上述分析,本文提出了一种顾及空间信息与FCN的高分辨率遥感影像分类方法。首先,通过改进FCN网络的卷积层结构,将高分辨率遥感影像及其高程信息同时作为输入数据进行训练,采用FCN方法进行粗分类;接着,使用CRF模型进行精分类得到最终分类结果,并通过对比实验依据主观视觉效果和客观定量指标对该方法进行了验证。
1 方法与原理本文提出的顾及空间信息与FCN的高分辨率遥感影像分类方法整体流程如图 1所示。该方法分为训练和分类两个阶段。在训练阶段,首先,将预处理后的训练数据输入改进后的FCN网络得到由底层到高层的特征映射,再通过Softmax分类器得到类别概率图;然后,采用自适应矩估计(adaptive moment estimation, Adam)梯度下降算法优化交叉熵损失函数,迭代更新FCN网络参数,构建分类网络模型。在分类阶段,首先,将待分类影像(图 1中真正射影像(true ortho photo, TOP))及其对应的数字表面模型(digital surface model, DSM)输入至训练得到的网络模型和Softmax分类器得到的类别概率图;然后,将概率图和影像分别作为一元势数和二元势数输入CRF模型[19]获得最终的分类结果。
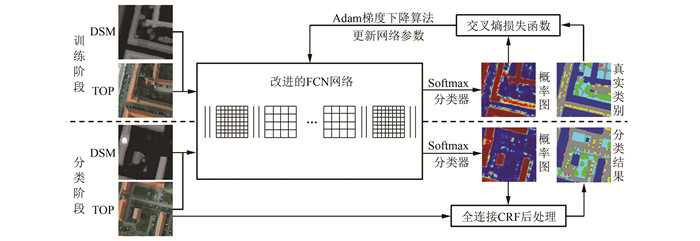 |
| 图 1 本文方法流程图 Fig.1 Flow Chart of Proposed Approach |
1.1 FCN网络结构
FCN通过将CNN中的全连接层卷积化并加入反卷积层,使得经池化层降采样后的特征图的分辨率恢复至与输入影像一致,同时采用跃层结构将最后3层池化层上采样的结果分步融合,从而获得像素水平的分类结果。本文构建的FCN网络结构如图 2所示,主要包括输入输出层、卷积层、池化层和反卷积层。
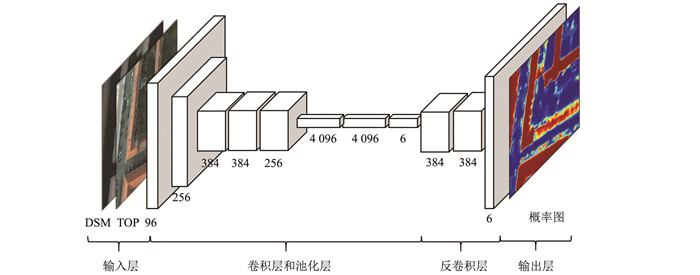 |
| 图 2 本文的FCN网络结构示意图 Fig.2 Structure Schematic Diagram of Proposed FCN |
1) 在卷积层中,由上一层获得的特征映射输入当前层进行卷积运算,然后通过激活函数进行非线性化,从而获得更高层次的特征映射为:
| $ x_j^l = f(\sum\limits_i {x_i^{l - 1}} \otimes k_{ij}^l + b_j^l) $ | (1) |
式中,xjl为输出特征映射;l为当前层;⊗为卷积运算符;xil-1为输入特征映射;kijl为卷积核;bjl为偏置项;f(·)为激活函数。常用的激活函数包括tanh函数、sigmoid函数和ReLU函数等。然而,在训练过程中,tanh函数、sigmoid函数由于存在“梯度消失”特性,导致算法的时间复杂度相对较高[20]。因此,本文使用ReLU函数作为激活函数,以提高影像分类效率。
为了综合利用影像的光谱信息和空间信息,本文增加了卷积层的特征通道数,使其适应于本文使用的输入数据。
2) 在池化层中,通过滑动窗口法将输入特征映射划分为多个大小为n像素×n像素的不重叠子块,然后统计子块内的像素的最大值(或平均值)作为池化特征,从而获得降采样之后的特征映射。池化操作通过简化网络复杂度避免训练结果过拟合,同时可以增强特征的平移不变性,并减小特征参数的计算复杂度。
3) 反卷积层。在多个池化层的降采样作用下,卷积层获得特征映射的分辨率逐层降低。为获得与输入影像分辨率一致的分类图,需要将低分辨率的特征映射输入反卷积层,经双线性内插得到上采样之后的结果为:
| $ \begin{array}{*{20}{c}} {{y_{ij}} = \sum\limits_{\alpha ,\beta = 0}^1 | 1 - \alpha - \{ i/f\} |}\\ {|1 - \beta - \{ j/f\} |{x_{|j/f|{ + _\alpha },|j/f| + \beta }}} \end{array} $ | (2) |
式中,f为上采样因子;{·}表示分数部分;x|i/f +α, j/f +β|表示输入的特征映射;yij为输出结果。
通过一次上采样得到的粗粒度特征映射无法反映原始影像的细节。因此,需要联合不同层次的特征,即将后3个池化层得到的特征映射分别上采样,然后分步融合,从而得到精化后的上采样结果,同时最大限度保留了特征的稳定性。
1.2 Softmax分类器Softmax分类器作为一种监督学习算法,通常用于解决多分类问题。若有m个训练样本{(x(1), y(1)), (x(2), y(2)), …, (x(m), y(m))}。其中,x(i)∈Rn+1为输入特征,y(i)∈{0, 1, …, k}为对应的真实类别标签。使用一个k维向量hθ(x)表示给定样本x(i)属于类别j的概率p(y(i)=j|x(i); θ),hθ(x)的形式如下:
| $ \begin{array}{l} {\mathit{\boldsymbol{h}}_\mathit{\boldsymbol{\theta }}}(x) = \left[ {\begin{array}{*{20}{c}} {p({y^{(i)}} = 1|{x^{(i)}};\mathit{\boldsymbol{\theta }})}\\ {p({y^{(i)}} = 2|{x^{(i)}};\mathit{\boldsymbol{\theta }})}\\ \vdots \\ {p({y^{(i)}} = k|{x^{(i)}};\mathit{\boldsymbol{\theta }})} \end{array}} \right] = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{1}{{\sum\limits_{j = 1}^k {{{\rm{e}}^{\mathit{\boldsymbol{\theta }}_j^{\rm{T}}{x^{(i)}}}}} }}\left[ {\begin{array}{*{20}{c}} {{{\rm{e}}^{\mathit{\boldsymbol{\theta }}_1^{\rm{T}}{x^{(i)}}}}}\\ {{{\rm{e}}^{\mathit{\boldsymbol{\theta }}_2^{\rm{T}}{x^{(i)}}}}}\\ \vdots \\ {{{\rm{e}}^{\mathit{\boldsymbol{\theta }}_k^{\rm{T}}{x^{(i)}}}}} \end{array}} \right] \end{array} $ | (3) |
式中,θ1,θ2,…,θk表示待求模型参数。
Softmax分类器的代价函数如下:
| $ J(\mathit{\boldsymbol{\theta }}) = - \frac{1}{m}\left[ {\sum\limits_{i = 1}^m {\sum\limits_{j = 1}^k I } \{ {y^{(i)}} = j\} {\rm{log}}\frac{{{{\rm{e}}^{\mathit{\boldsymbol{\theta }}_j^{\rm{T}}{x^{(i)}}}}}}{{\sum\limits_{l = 1}^k {{{\rm{e}}^{\mathit{\boldsymbol{\theta }}_j^{\rm{T}}{x^{(i)}}}}} }}} \right] $ | (4) |
式中,I{·}为指示函数,当表达式为真时取值为1,否则取值为0。
由式(4)可知,Softmax分类器先将获得的特征值在指数域归一化映射为概率值,然后使用交叉熵代价函数构建目标函数。
1.3 Adam梯度下降算法式(4)所示目标函数的求解通常使用随机梯度下降(stochastic gradient descent, SGD)算法为:
| $ {\mathit{\boldsymbol{\theta }}_t} = {\mathit{\boldsymbol{\theta }}_{t - 1}} - \Delta {\mathit{\boldsymbol{\theta }}_t} $ | (5) |
式中,θt和θt-1分别为优化后和优化前的参数;Δθt=-η×gt为参数在当前迭代周期中的增量,其中,η为学习率,gt=▽θt-1f(θt-1)为优化前参数的梯度。
SGD算法对于所有参数采取同样的步幅进行优化,求解过程中容易发生扰动,降低优化速度,并且在某些情况可能陷入鞍部。因此,本文采用改进后的Adam梯度下降算法求解目标函数,此时,有:
| $ \Delta {\mathit{\boldsymbol{\theta }}_t} = - \eta \times \frac{{{{\hat m}_t}}}{{\sqrt {{{\hat n}_t} + \varepsilon } }} $ | (6) |
其中,
| $ {{{\hat m}_t} = \frac{{{m_t}}}{{1 - {\mu ^t}}}} $ | (7) |
| $ {{{\hat n}_t} = \frac{{{n_t}}}{{1 - {v^t}}}} $ | (8) |
| $ {{m_t} = \mu \times {m_{t - 1}} + (1 - \mu ) \times {g_t}} $ | (9) |
| $ {{n_t} = \nu \times {n_{t - 1}} + (1 - \nu ) \times g_t^2} $ | (10) |
式中,mt、nt分别表示对梯度gt的一阶矩估计和二阶矩估计;
Adam梯度下降算法通过动态调整每个参数的优化步幅使得求解过程趋于平稳,从而可以使用较大学习率,进而加快优化速度,避免困于鞍部。
1.4 条件随机场为解决采用训练阶段获得的网络模型进行影像分类产生的锯齿边缘和噪声问题,本文使用条件随机场作为分类阶段的后处理方法对分类结果进行优化。如图 3所示,栅格的每个节点对应影像中一个像素的标签类型和观测值,而像素与像素连接的边构成了一个条件随机场。
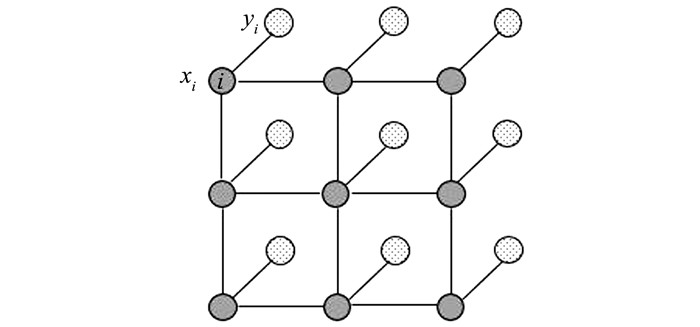 |
| 图 3 条件随机场模型 Fig.3 Conditional Random Fields Model |
条件随机场作为符合Gibbs分布的无向图模型,其相应的Gibbs能量函数形式如下:
| $ E(x) = \sum\limits_i {{\psi _i}} ({x_i}) + \sum\limits_{ij} {{\psi _{ij}}} ({x_i},{x_j}) $ | (11) |
式中,xi、xj分别表示像素i、j的类别标签值;ψi(xi)= -logP(xi)表示一元势数。其中,P(xi)为Softmax分类器输出的概率值;ψij(xi, xj)表示二元势数,其表达式为:
| $ {\psi _{ij}}({x_i},{x_j}) = \mu ({x_i},{x_j})\sum\limits_{m = 1}^K {{w_m}} \times {k^m}({f_i},{f_j}) $ | (12) |
式中,μ(xi, xj)为指示函数,当xi≠xj时,μ(xi, xj)值为1,否则值为0;wm表示权重参数;km(·)表示特征f的高斯核函数。本文采用的核函数形式如下:
| $ \begin{array}{*{20}{l}} {k({f_i},{f_j}) = {w_1}{\rm{exp}}\left( { - \frac{{{{\left\| {{p_i} - {p_j}} \right\|}^2}}}{{2\sigma _\alpha ^2}} - \frac{{{{\left\| {{I_i} - {I_j}} \right\|}^2}}}{{2\sigma _\beta ^2}}} \right) + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {w_2}{\rm{exp}}\left( { - \frac{{{{\left\| {{p_i} - {p_j}} \right\|}^2}}}{{2\sigma _\gamma ^2}}} \right)} \end{array} $ | (13) |
式中,p为输入影像的像素坐标值;I为像素颜色值;σα、σβ和σγ为高斯核的尺度;w1、w2分别表示两个核函数的权重参数。
由式(10)和式(11)可知,二元势数通过描述像素间的“坐标-颜色”约束关系,提高相似度高的像素点被归为同一类别的概率,从而获得边缘平滑的分类结果。
2 实验与分析 2.1 实验数据与预处理本文选取的实验数据为ISPRS WG II/4公用数据集,该数据集摄于德国Potsdam地区,包含地面、建筑、低矮植被、树木、车辆和杂物共6类典型地物,地面分辨率为0.05 m,像幅为6 000像素×6 000像素。本文选择了其中24幅带有类别标注的RGB波段的TOP和对应DSM进行实验,其中22幅作为训练集和验证集用于训练阶段,另外2幅作为测试集用于分类阶段。
为避免训练结果过拟合,需对训练数据进行预处理,具体步骤为:首先,将22幅TOP和对应DSM分割为4 950幅大小为400像素×400像素的影像块,其中,4 000幅作为训练集,其余作为验证集,然后对训练集的TOP采取翻转、转置和旋转操作,同时对影像对比度、饱和度、亮度和色调加入随机扰动,之后与对应DSM叠加得到最终训练集数据。验证集与训练集数据则由TOP与DSM直接叠加获得。
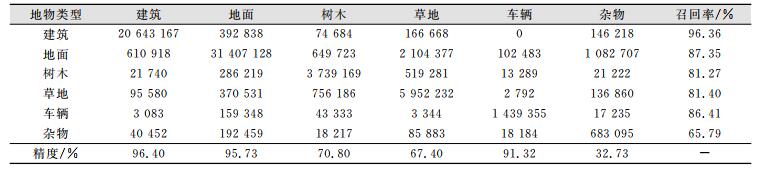
2.2 实验结果与分析为验证本文方法的可行性和有效性,根据输入数据的不同(是否有DSM)以及分类策略的不同(是否有CRF后处理)进行了4组对比实验,同时,为证明本文方法的优越性,利用面向对象的最近邻法[5](object oriented K-nearest neighbor,OO-KNN)和SVM[21]等传统方法开展了分类实验,具体实验方案及总体分类结果如表 1所示,其中方案6为本文方法。表 2以人工目视分类结果图为基础统计了本文方法在测试集上分类结果的混淆矩阵(像元个数),无单位。
| 表 1 ISPRS WG II/4数据集实验方案概况 Tab.1 Overview of Different Experimental Schemes on ISPRS WG II/4 Dataset |
 |
| 表 2 本文方法分类混淆矩阵 Tab.2 Confusion Matrix of Proposed Approach |
 |
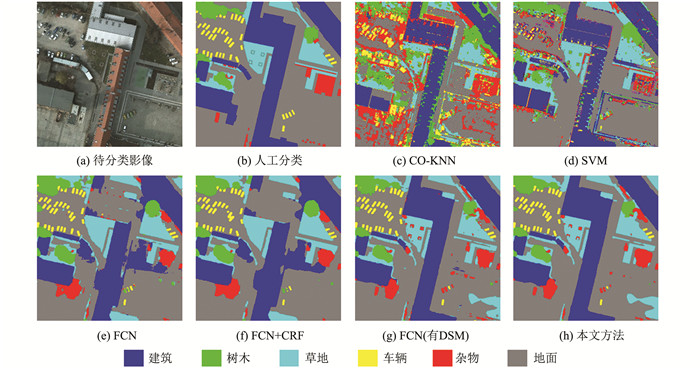
ISPRS WG II/4数据集分类结果如图 4所示。
 |
| 图 4 ISPRS WG II/4数据集分类结果图 Fig.4 Classification Results on ISPRS WG II/4 Dataset |
图 4(a)截取了待分类影像中一块大小为2 000像素×2 000像素的区域作为示例;图 4(b)给出了其人工标注的正确类别;图 4(c)是采用面向对象的K近邻法分类的结果,可以看到地面区域和建筑区域存在严重的噪声,且建筑与地面、杂物等地物混淆严重;图 4(d)采用了SVM分类方法,地面区域的噪声得到抑制,建筑的分类精度有较大提高,但依然存在建筑边缘细小区域错分的现象,并且难以正确区分车辆、杂物等目标相对较小的地物;从图 4(e)、图 4(f)可以看出,FCN方法进一步改善了分类效果,地面噪声得到消除,车辆等小地物得以良好区分;然而,仅使用TOP作为训练数据时,FCN方法分类结果中建筑与地面存在严重的混淆问题,而加入DSM参与训练后,该问题得到较好解决(见图 4(g)、图 4(h))。与此同时,通过对比图 4(e)与图 4(f)(或图 4(g)与图 4(h))可以发现,使用CRF进行后处理之后,建筑区域原先的锯齿边缘变得更为平滑,存在细小破碎面片的问题也得到了进一步改善。
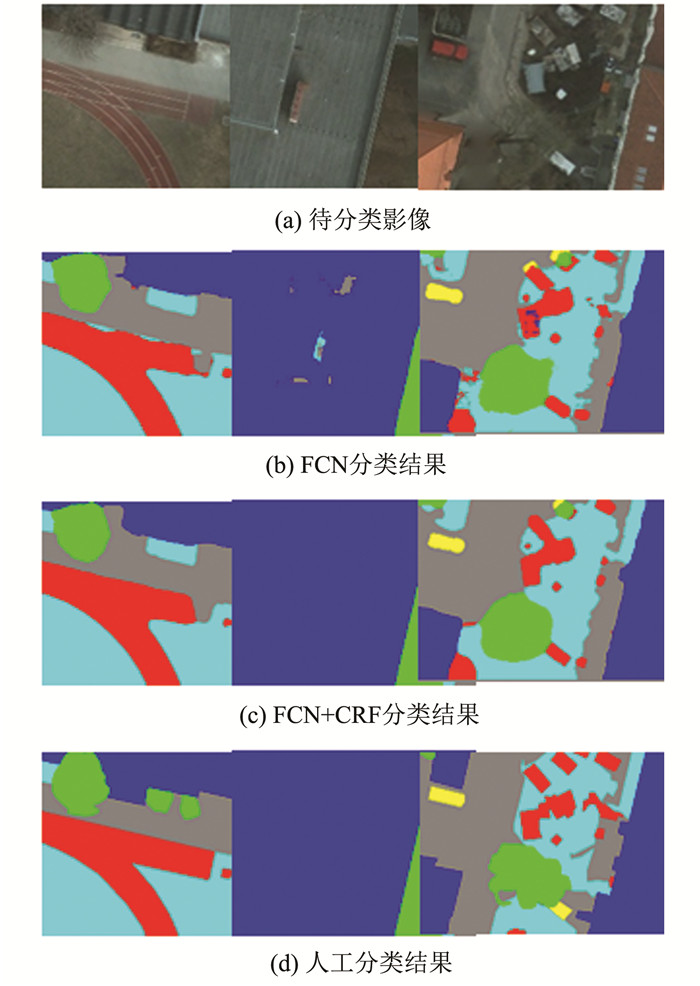
图 5展示了分类结果图的几处细节,通过对比FCN方法和FCN+CRF方法的分类结果,进一步说明了CRF的平滑效果。可以看到,CRF不但可以平滑边缘、移除细小杂物,还可以填补建筑物的空洞,使分类结果更接近人工分类效果。
 |
| 图 5 CRF平滑效果示意图 Fig.5 Smooth Effect Schematic Diagram of CRF |
表 1统计了各方法分类结果的总体精度和Kappa系数。从表中可以看出,FCN方法(方案3)对比OO-KNN和SVM方法分别有21.50%和9.26%的精度提升,这是由于FCN方法在训练阶段可以通过卷积层学习到大量高层语义特征,从而大大提高了不同地物间的区分度。加入DSM训练后(方案5),总体精度进一步提升了3.69%,反映出高程信息在区分水泥房顶与水泥地面、草地与树木等特征相似的地物时起到了重要作用。使用CRF进行后处理后(方案6),总体精度得到了一定程度的提升,同时结合图 4(g)和图 4(h)可以看出,锯齿边缘以及噪声问题得到改善,分类的目视效果得到较大提升。同时,本文方法的Kappa系数为0.830 3,高于其他各方法,表明本文方法的整体分类性能具有一定优势。
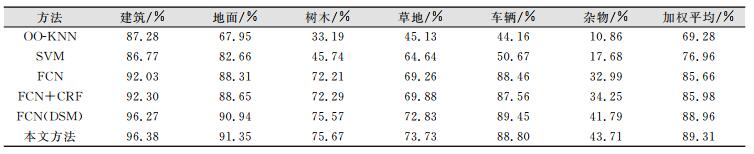
表 3对比了由各种方法分类得到的各个类别的F1测度:
| 表 3 不同方法分类结果的F1测度对比 Tab.3 Comparison of F1 Score Between Different Approaches |
 |
| $ {F_1} = 2PR/(P + R) $ | (14) |
式中,P为正确率;R为召回率。
通过对表 3进一步分析发现,本文方法对车辆的分类效果比方案5略有下降,这是由于在后处理过程中CRF对细小地物存在一定的平滑效果。然而,对其他地物,本文方法的分类效果均优于其他方法,特别是对建筑物和树木的分类精度提升较大,且全部地物的平均F1值为89.31%,建筑和地面的F1值分别达96.38%和91.35%,能够较好地满足实际应用的需求。
3 结束语针对传统遥感影像分类中存在的特征选择困难和空间信息缺乏等问题,本文提出顾及空间信息与FCN的高分辨率遥感影像分类方法,将全卷积神经网络与条件随机场方法结合起来用于高分辨率遥感影像分类。该方法综合考虑了高程信息与空间约束在遥感影像分类中的影响,实现了像素水平的分类。基于本文提出的方法,使用ISPRS WG II/4数据集进行了多组对比实验。实验表明,本文方法可有效提高分类精度,减少分类噪声,在视觉效果以及定量评价上均优于FCN以及面向对象的KNN和SVM等传统分类方法,实验结果同时证明了光谱信息结合高程信息用于高分辨率遥感影像分类的有效性。
| [1] |
胡文元, 聂倩, 黄小川. 基于纹理和光谱信息的高分辨率遥感影像分类[J]. 测绘信息与工程, 2009, 34(1): 16-18. |
| [2] |
张文君, 顾行发, 陈良富, 等. 基于均值-标准差的K均值初始聚类中心选取算法[J]. 遥感学报, 2006(5): 715-721. |
| [3] |
张怡然, 陈锐, 张文婷, 等. 非等权距离改进的FCM多波段遥感影像监督分类算法[J]. 测绘地理信息, 2016, 41(4): 65-71. |
| [4] |
张帅, 钟燕飞, 张良培. 自适应差分进化的遥感影像自动模糊聚类方法[J]. 测绘学报, 2013, 42(2): 239-246. |
| [5] |
薛梦姣, 陈刚, 张笑, 等. 面向对象的资源三号卫星影像分类研究[J]. 测绘通报, 2015(7): 42-45. |
| [6] |
佃袁勇, 杨光, 方圣辉. 傅里叶谱纹理和光谱信息结合的高分辨率遥感影像地表覆盖分类[J]. 武汉大学学报·信息科学版, 2017, 42(3): 362-368. |
| [7] |
Lecun Y, Bottou L, Bengio Y, et al. Gradient-Based Learning Applied to Document Recognition[J]. Proceedings of the IEEE, 1998, 86(11): 2278-2324. DOI:10.1109/5.726791 |
| [8] |
Hinton G E, Salakhutdinov R R. Reducing the Dimensionality of Data with Neural Networks[J]. Science, 2006, 313(5786): 504-507. DOI:10.1126/science.1127647 |
| [9] |
Lecun Y, Bengio Y, Hinton G. Deep Learning[J]. Nature, 2015, 521(7553): 436-444. DOI:10.1038/nature14539 |
| [10] |
Krizhevsky A, Sutskever I, Hinton G E. ImageNet Classification with Deep Convolutional Neural Networks[J]. Communications of the ACM, 2017, 60(6): 84-90. DOI:10.1145/3065386 |
| [11] |
Lagrange A, Le Saux B, Beaupere A, et al.Benchmarking Classification of Earth-Observation Data: From Learning Explicit Features to Convolutional Networks [C]. Geoscience and Remote Sensing Symposium, Milan, Italy, 2015
|
| [12] |
Penatti O A B, Nogueira K, Dos Santos J A. Do Deep Features Generalize from Everyday Objects to Remote Sensing and Aerial Scenes Domains?[C]. Computer Vision and Pattern Recognition Workshops, Boston, USA, 2015
|
| [13] |
Long J, Shelhamer E, Darrell T.Fully Convolutional Networks for Semantic Segmentation[C]. IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 2015
|
| [14] |
Marmanis D, Wegner J D, Galliani S, et al. Senmantic Segmentation of Aerial Imageswith an Ensemble of CNNs[C]. ISPRS Annals of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Prague, Czech Republic, 2016
|
| [15] |
Maggiori E, Tarabalka Y, Charpiat G, et al. Convolutional Neural Networks for Large-Scale Remote-Sensing Image Classification[J]. IEEE Transactions on Geoscienceand Remote Sensing, 2017, 55(2): 645-657. DOI:10.1109/TGRS.2016.2612821 |
| [16] |
Fu G, Liu C, Zhou R, et al. Classification for High Resolution Remote Sensing Imagery Using a Fully Convolutional Network[J]. Remote Sensing, 2017, 9(6): 498. |
| [17] |
李祖传, 马建文, 张睿, 等. 利用SVM-CRF进行高光谱遥感数据分类[J]. 武汉大学学报·信息科学版, 2011, 36(3): 306-310. |
| [18] |
王少宇, 焦洪赞, 钟燕飞. 条件随机场模型约束下的遥感影像模糊C-均值聚类算法[J]. 测绘学报, 2016, 45(12): 1441-1447. DOI:10.11947/j.AGCS.2016.20150621 |
| [19] |
Krahenbuhl P, Koltun V. Efficient Inference in Fully Connected CRFs with Gaussian Edge Potentials[J]. Advances in Neural Information Processing Systems, 2011, 24: 109-117. |
| [20] |
Glorot X, Bordes A, Bengio Y. Deep Sparse Rectifier Neural Networks[C]. International Conference on Artificial Intelligence and Statistics, La Palma, Canary Islands, 2012
|
| [21] |
Mountrakis G, Im J, Ogole C. Support Vector Machines in Remote Sensing: A Review[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2011, 66(3): 247-259. DOI:10.1016/j.isprsjprs.2010.11.001 |
 2020, Vol. 45
2020, Vol. 45


