| 精密单点定位收敛时间分析 |
精密单点定位(precise point positioning,PPP)技术是利用载波相位观测值和国际GNSS服务组织(International Global Navigation Satellite System Service, IGS)提供的精密轨道和钟差产品的高精度定位方法[1, 2]。目前,PPP技术可以实现静态从mm到cm级,动态cm到dm级的定位精度[3],在气象学、地震学等领域得到广泛应用[4, 5],但收敛时间一直是制约PPP大规模使用的一个重要因素。为加快PPP收敛,文献[6-8]提出了加快PPP收敛速度的方法;郑作亚等分析了影响PPP收敛的主要因素并提出了改善PPP收敛速度的建议[9],但是没有分析PPP收敛到不同定位精度所需要的时间;林晓静等分析了不同接收机类型、测站地理位置及PDOP(position dilution of precision)值对PPP收敛的影响,一定条件下给出了不同条件下PPP静态解和动态解收敛到dm级所需要的时间[10],但其实验数据较少并且没有给出收敛时间的置信度。由此可见,PPP收敛速度与观测值质量、卫星几何构形以及采样间隔等因素有关,需要约10~30 min的收敛时间,且不同观测条件下需要的收敛时间不同。鉴于PPP目前没有统一有效地收敛判断方法。因此,在实际生产过程中,为保证达到所需要的定位精度,一般都需要等待比收敛时间更长的观测时间,降低了PPP的作业效率。鉴于此,本文利用168个IGS跟踪站共约168 d的观测数据,分析了在不同观测条件以及不同的置信度下,传统双频无电离层组合PPP算法收敛到不同定位精度所需要的时间,为精度需求不同的用户提供一定的参考依据。
1 精密单点定位模型PPP算法为消除电离层误差影响,一般采用无电离层相位和伪距观测值。其基本观测方程可以表示为:
| $ \left\{ \begin{array}{l} {P_{{\rm{IF}}}} = \rho + c\Delta {t_r} - c\Delta {t^i} + {\rm{Trop}} + \varepsilon ({P_{{\rm{IF}}}})\\ {\mathit{\Phi }_{{\rm{IF}}}} = \rho + c\Delta {t_r} - c\Delta {t^i} + {\rm{Trop + }}\lambda N + \varepsilon ({\mathit{\Phi }_{{\rm{IF}}}}) \end{array} \right. $ | (1) |
式中,PIF和ΦIF分别代表无电离层伪距和相位观测值,单位为m;ρ表示测站和卫星之间的距离,包含天线相位中心、天线相位缠绕、地球固体潮、相对论效应和地球自转等误差改正;c为光速;Δtr和Δti分别表示接收机钟差和卫星钟差;Trop表示对流层误差;λ表示无电离层组合波长;N表示无电离层组合模糊度;ε(PIF)和ε(ΦIF)表示未模型化的误差和观测噪声。本文使用自编软件进行PPP处理,观测值采用无电离层组合相位和伪距观测值,截止高度角为10°,定权策略为高度角定权,卫星轨道和钟差分别采用德国波茨坦地学研究中心(Helmholtz-Centre Potsdam-German Research Centre for Geosciences, GfZ)最终轨道和钟差产品,天线相位缠绕、天线相位中心、固体潮、相对论改正和地球自转进行模型改正,不考虑多路径效应的影响,伪距硬件延迟采用CODE(center oborbit deter mination Europe)提供的DCB(different code Bias)进行改正,位置参数和接收机钟差采用白噪声估计,对流层干分量采用Saastamoine模型进行改正,湿分量采用随机游走的方法进行处理,不固定模糊度。
2 数据处理本文选取IGS全球分布约168个测站2014年每个月前两周共约168天的观测数据,比较分析PPP动态解定位收敛速度。数据处理时,真值坐标从SINEX(solution independent exchange format)周解文件中提取。由于低纬度地区观测时段较多,全球卫星导航系统(global navigation satellite system,GLONASS)存在可观测卫星数少于4颗的情况,无法采用单一GLONASS系统实现PPP定位[11]。因此,全球范围内仅分析单GPS PPP和GPS+GLONASS PPP的收敛速度,其测站分布如图 1所示。
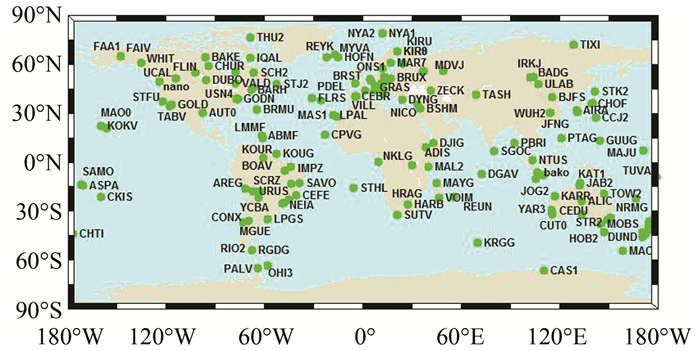 |
| 图 1 测站分布图 Fig.1 Distribution of Stations |
本文主要分析不同卫星系统、不同卫星几何构形和测站地理位置对PPP收敛的影响,将各测站全天的观测数据分割成5 min、10 min、15 min、20 min、25 min、30 min、40 min、50 min、60 min、90 min、120 min、180 min、240 min等不同时长的观测数据, 分别统计不同观测时长的观测数据所能达到的定位精度来分析PPP的收敛速度。
3 结果分析图 2给出了单GPS PPP的收敛时序图。由图 2可知,N方向收敛速度最快,其次是E方向,高程方向收敛速度最慢。68.3%置信区间下,单GPS PPP在5 min内N、E、U 3个方向便可收敛到dm级;收敛到优于10 cm时,N方向大约需要15 min,而E和U方向则需要约39 min。而在95.4%置信区间下,5 min内平面可以收敛到dm级,高程可以收敛到优于1.2 m;收敛到10 cm时,N方向需要约52 min,E方向需要约150 min,而U方向需要约240 min。
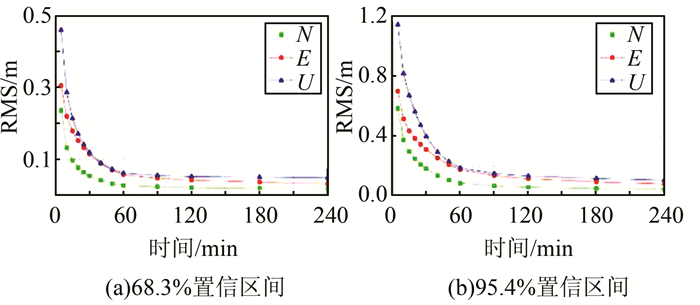 |
| 图 2 单GPS PPP收敛时序图 Fig.2 Convergence Accuracy of GPS PPP |
图 3给出了GPS+GLONASS PPP的收敛时序图。从图 3中可以看出,加入GLONASS观测数据后,PPP的收敛速度明显加快。5 min内68.3%置信区间下N、E、U 3个方向定位精度分别提高到0.18 m、0.25 m和0.33 m,提高约24%、18%和28%;当收敛到优于10 cm时,N方向减少到约8 min,而E和U方向减少到约15 min,提高约47%、62%和62%。在95.4%置信区间下,5 min内定位精度提高到0.4 m、0.6 m和0.75 m,提高约32%、14%和35%;收敛到10 cm时,N方向减少到约17 min,E方向减少到约45 min,而U方向减少到约55 min,提高了约67%、70%和77%。
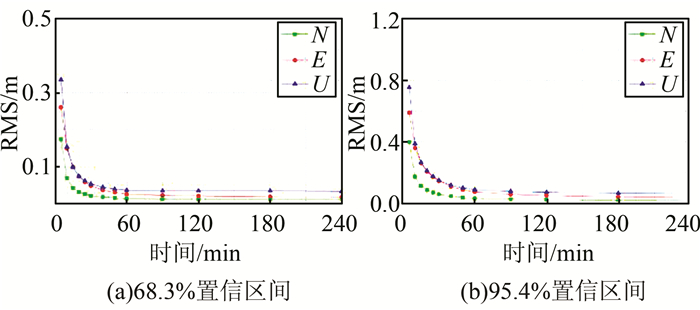 |
| 图 3 GPS+GLONASS组合PPP收敛时序图 Fig.3 Convergence Time of GPS/GLONASS Combined PPP |
图 4给出了不同纬度区域GPS PPP和GPS+GLONASS PPP N、E、U方向在68.3%置信区间下收敛到不同时间所达到的精度。图 4中横坐标代表不同的收敛时间,单位为min;纵坐标代表纬度;图中不同的颜色代表不同的收敛精度。可以看出,由于GPS卫星星座设计特点,不同纬度区域单GPS PPP收敛速度存在一定差异。N方向收敛速度在高纬度地区比低纬度区域慢,尤其是当超过50°时,其收敛速度最慢,在10°~30°时,其收敛速度最快;E方向则随着纬度降低收敛速度变慢,其中赤道地区收敛速度最慢;对于U方向,纬度高于50°的区域收敛速度明显快于纬度低于50°的区域,区域位于10°~30°收敛速度最慢。组合PPP在N、E方向上的收敛趋势与单GPS PPP N、E方向的收敛趋势基本相同,U方向的收敛趋势略有不同,组合PPP U方向在赤道附近收敛最慢。
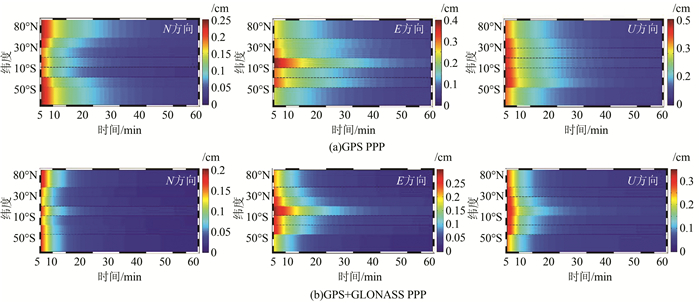 |
| 图 4 68.3%置信区间下单GPS PPP和GPS+GLONASS组合PPP收敛精度分布图 Fig.4 Convergence Accuracy Distribution Map of GPS PPP and GPS/GLONASS Combined PPP in 68.4% Confidence Interval |
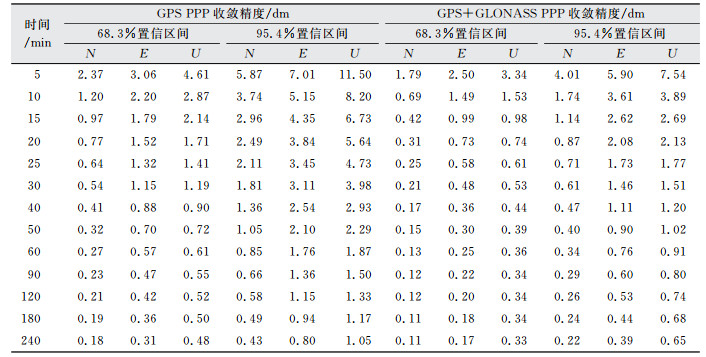
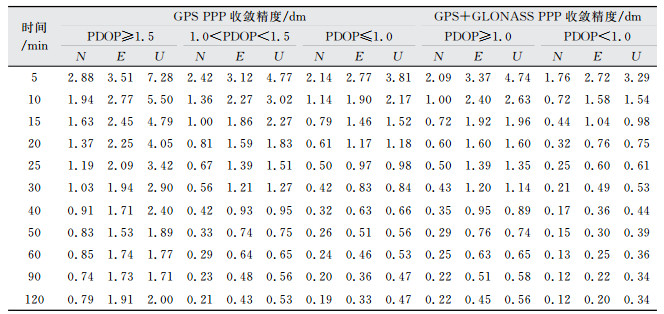
图 5和图 6给出了观测时段内平均PDOP(position dilution of precision)值不同时单GPS PPP和GPS+GLONASS PPP的收敛时序图。由于GPS+GLONASS PPP中,可用卫星数较多,平均PDOP值大于1.5的观测时段较少。因此仅统计平均PDOP值分别大于1.0和小于1.0的收敛速度。由图 5、图 6可以看出,PDOP值的不同对单GPS PPP和组合PPP收敛速度影响较明显,PDOP值越大,收敛速度越慢。另外,从图 6可以看出,当PDOP值小于1.0的收敛速度比介于1.0~1.5的收敛速度提高并不明显,说明当卫星几何构型达到一定程度时,增加卫星对收敛速度的贡献有限。部分策略的收敛精度统计结果如表 1和表 2所示。表 1为GPS PPP和GPS+GLONASS PPP在68.3%和95.4%置信区间下的收敛精度统计表;表 2为不同PDOP值下的GPS PPP和GPS+GLONASS PPP收敛精度统计表。
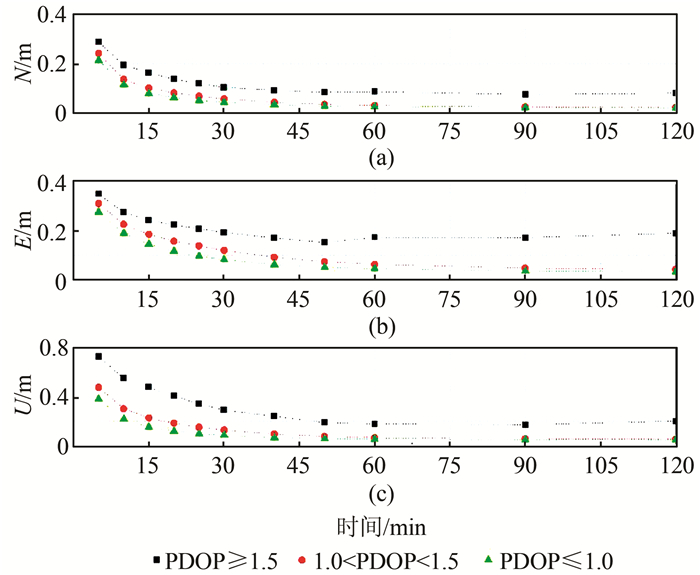 |
| 图 5 不同PDOP值时单GPS PPP收敛时序图 Fig.5 Convergence Time of GPS PPP in Different PDOP |
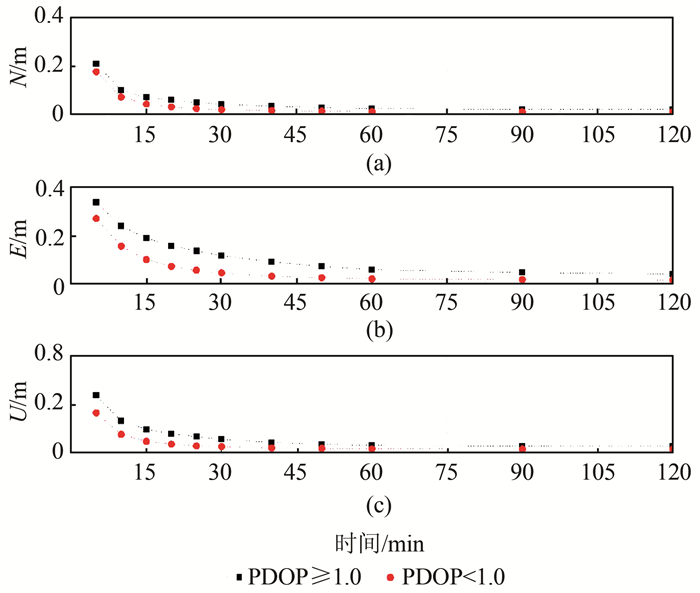 |
| 图 6 不同PDOP值时GPS+GLONASS PPP收敛时序图 Fig.6 Convergence Time of GPS+GLONASS Combined PPP in Different PDOP |
| 表 1 GPS PPP和GPS+GLONASS PPP收敛精度 Tab.1 GPS PPP and GPS+GLONASS PPP Convergence Accuracy |
 |
| 表 2 不同PDOP值时GPS PPP和GPS+GLONASS PPP收敛精度 Tab.2 GPS PPP and GPS+GLONASS Combined PPP Convergence Accuracy in Different PDOP |
 |
4 结束语
本文利用全球IGS测站分析了不同系统、卫星几何构型和测站地理位置对PPP收敛时间的影响,并且给出了单GPSPPP和GPS+GLONASS组合PPP在不同置信区间下收敛到不同定位精度所需要的时间,为PPP用户的实际生产提供一定的参考依据。
1) 单GPS PPP和GPS+GLONASS组合在PPP N、E、U方向68.3%和95.4%的置信区间下收敛5 min可以达到的精度以及3个方向收敛到优于10 cm时所需要的时间,GPS+GLONASS组合PPP的收敛速度加快是由于加入了GLONASS观测值,成倍的增加了卫星个数,改善了GPS+GLONASS卫星的几何构型。
2) 不同纬度区域PPP的收敛速度存在一定差异,这与测站地理位置的不同造成所受电离层等误差的影响不同有关。由于GLONASS在设计星座时对高纬度的覆盖率要高于GPS,导致赤道附近观测到的GLONASS卫星数较少,所以组合PPP高程方向在赤道收敛最慢。
3) 在一定条件下,PDOP值会影响单GPS PPP和GPS+GLONASS组合PPP的收敛速度。
| [1] |
Zumberge J F, Heflin M B, Jefferson D C, et al. Precise Point Positioning for the Efficient and Robust Analysis of GPS Data from Large Networks[J]. Journal of Geophysical Research: Solid Earth, 1997, 102(B3): 5005-5017. DOI:10.1029/96JB03860 |
| [2] |
Kouba J, Heroux P. Precise Point Positioning Using IGS Orbit and Clock Products[J]. GPS Solutions, 2001, 5(2): 12-28. DOI:10.1007/PL00012883 |
| [3] |
Bisnath S, Gao Y. Current State of Precise Point Positioning and Future Prospects and Limitations[J]. Observing Our Changing Earth, 2008, 133(4): 615-623. |
| [4] |
张帝, 高雅萍, 许双安. GPS技术在矿区沉降监测中的应用[J]. 测绘地理信息, 2012, 37(2): 22-24. |
| [5] |
杨军建, 姚宜斌, 许超钤, 等. 不同在线PPP技术得到的ZTD对比与精度分析[J]. 测绘地理信息, 2015, 40(6): 11-14. |
| [6] |
Li X X, Zhang X H, Ge M R. Regional Reference Network Augmented Precise Point Positioning for Instantaneous Ambiguity Resolution[J]. Journal of Geodesy, 2011, 85(3): 151-158. DOI:10.1007/s00190-010-0424-0 |
| [7] |
郑艳丽, 刘经南, 宋伟伟, 等. 基于区域增强信息的PPP的快速收敛算法[J]. 大地测量与地球动力学, 2012, 32(4): 111-115. |
| [8] |
Shen Xiaobing. Improving Ambiguity Convergence in Carrier Phase-Based Precise Point Positioning[D]. Calgary, Canada: University of Calgary, 2002 https://www.researchgate.net/publication/246435400_Improving_Ambiguity_Convergence_in_Carrier_Phase-based_Precise_Point_Positioning
|
| [9] |
郑作亚, 党亚民, 卢秀山, 等. GPS精密单点定位中影响收敛时间的因素及措施分析[J]. 大地测量与地球动力学, 2009, 29(5): 107-111. |
| [10] |
林晓静, 张小红, 郭斐, 等. 影响精密单点定位收敛速度的因素分析[J]. 测绘信息与工程, 2010, 35(3): 10-12. |
| [11] |
王祖光, 杨开伟, 王宝成. GPS/GLONASS组合系统性能分析[J]. 测绘通报, 2010(6): 38-40. |
 2018, Vol. 43
2018, Vol. 43

