2. 南京信息工程大学 气象灾害预报预警与评估协同创新中心,南京 210044;
3. 南京信息工程大学风险治理与应急决策研究院,南京 210044
2. Collaborative Innovation Center for Forecast and Evaluation of Meteorological Disasters, Nanjing University of Information Science and Technology, Nanjing, 210044;
3. Research Center of Risk Management and Emergency Decision Making, Nanjing University of Information Science and Technology, Nanjing, 210044
在气候变暖的大背景下,全球暴雨的时空格局正在发生重大变化。中国饱受洪涝灾害侵扰,各流域暴雨强度和频次变化趋势并不一致(胡畔等,2021;谢五三和王胜,2010)。淮河流域位于我国东部(111°55'—121°20'E,30°55'—36°20'N),地跨河南、安徽、江苏及山东四省,属于东亚季风气候区,是中国南北气候的过渡地带。根据气候历史资料记载,淮河流域在1470—1991年期间发生一般等级洪涝灾害的年次数占总年数的30.8%,平均约3 a一次;严重(包括极严重) 的洪涝灾害发生频次为14.9%,约7 a发生一次(温克刚和丁一汇,2008)。由于上游落差大,中游平缓、支流水系复杂众多,以及历史上黄河长期夺淮入海等原因,淮河流域极易洪泛(刘倪和叶金印,2014)。因此,研究淮河流域的暴雨危险度,对于有效防治暴雨洪涝、降低灾害风险,切实保障人民群众生命财产安全和社会经济持续健康发展具有重大意义。
暴雨危险度是对暴雨致灾因子危险性程度的客观量化,国内外学者在区域暴雨危险度研究方法方面已经取得了一定的成果。在单因素量化分析方面,降水指标通常是对其趋势性和周期性等的分析(董旭光等,2014;孙燕和朱伟军,2013;闵爱荣等,2016)。趋势分析主要采用时间序列分析方法,如趋势拟合、平滑法等(黄垭飞等,2021;Shao et al.,2017);周期分析则主要采用各类谱分析法(魏凤英,2007),比较经典的有傅里叶变换(刘瑞鑫,2019)、小波分析(潘雅婧等,2012;刘毅等,2020)等。傅里叶变换是一种重要的时间序列数据处理方法,经过处理的数据中包含各种频率成分,但是丢失了数据的时间信息。小波变换可以将数据的频域信息和时域信息结合起来,克服了傅里叶变换的不足,但是由于小波基底选择不同,会对结果产生显著影响(郭建平和赵立龙,2021)。经验模态分解(Empirical Mode Decomposition,EMD)作为一种复杂数据分析方法,最早由Huang等(1998)提出,该方法既可以处理非线性、非平稳数据,也可以处理线性的、平稳的数据,具有良好的自适应属性,能够比其他方法更好地反映时间序列数据的物理意义(杨永锋和吴亚峰,2013)。因此,EMD方法在暴雨危险度的单因素分析中具有较好的应用潜力。在多因素综合量化分析方面,主要通过多指标加权综合方法实现对暴雨危险度的综合表达。例如,王晶等(2019)采用层次分析法考虑了降水强度、最多持续降水量、最长持续降水日、高程及河网密度,评估了淮河流域中上游地区洪涝灾害的致灾因子危险性;严志涛等(2021)采用加权求和方法考虑降水强度、最大持续降水量和最长持续降水天数指标,评估了西南四省的暴雨洪涝危险性。这些方法主要是将不同的影响因子进行相加或相乘,来代表总的危险性程度,存在明显不足。Copulas函数在刻画多变量之间相依结构方面具有明显优势,给暴雨危险度的多指标综合提供了新的思路。Copulas函数最早于1959年被提出,受计算能力限制,直到20世纪90年代末才被广泛地应用在金融领域,它以著名的Sklar定理为基础(Nelsen,2007;Rodriguez,2007),目前在气象灾害领域的应用逐步兴起,例如在沙尘暴、水文灾害等领域中的应用(李宁等,2013;Tosunoglu and Can, 2016)。
本文利用淮河流域及其周边站点降水数据,尝试采用EMD方法来分析反映暴雨危险度的单指标时间序列数据,再选择Copulas函数方法分析淮河流域暴雨的综合危险度,探讨淮河流域暴雨危险度的时空变化特征。
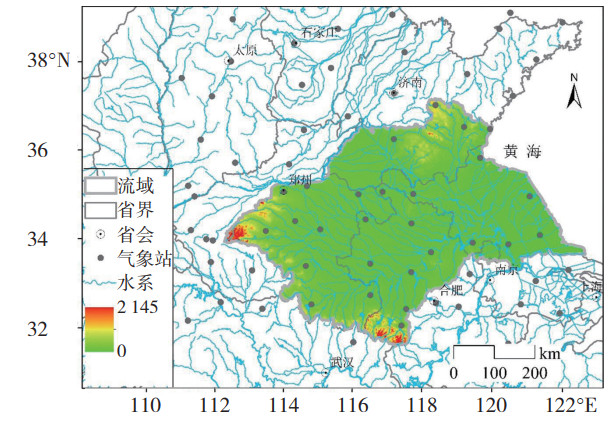
1 研究资料与方法 1.1 资料来源考虑到暴雨危险度分析的空间完整性,本研究区涵盖了整个淮河流域及其周边的部分区域。暴雨灾害风险的主要致灾因子为降水,参考相关文献(王晶等,2019;严志涛等,2021;郑艳等,2018;张正涛等,2014),选择淮河流域及其周边站点的历年年暴雨日数(日降水量≥ 50 mm的日数)作为频数指标,各站点历年的年最大日降水量作为强度指标来分析淮河流域暴雨危险度的时空规律。数据来源于中国气象局国家气象信息中心提供的1951—2017年淮河流域的降水日值数据集。通过对数据缺测值、异常值、均一性等方面的检验,最终选取淮河流域及其周边共68个站点(图 1)的逐日降水数据进行分析。其中部分站观测数据起始年份晚于1951年(所分析的时间序列最少不短于57 a,即最晚不迟于1960年),本文基于各站的观测数据对淮河流域暴雨危险度进行时空特征分析。
|
图 1 研究区概况及气象站点分布 Fig. 1 Study area and meteorological stations |
EMD方法的实质是将数据中存在的不同尺度或周期下的波动或变化趋势由高频向低频逐级提取出来,产生一系列不同尺度的分量,每个分量被称为一个特征模态函数(Intrinsic Mode Function,IMF) (Huang et al.,1998)。其中,IMF需要满足以下两个条件:
(1) 极值的个数和过零点的个数必须相等或相差一个;
(2) 在任何一点上,由局部极大值定义的上包络线和由局部极小值定义的下包络线的平均值为零。
EMD方法具体分解步骤为:
(1) 对于任意给定的时间序列数据x(t),求解其所有的极值点(极大值和极小值)。用三次样条函数连接所有极大值点形成上包络线u(t),连接所有极小值点形成下包络线b(t);
(2) 计算上下包络线的均值m(t),然后用原始数据x(t)减去m(t)得到新的序列h(t),计算方法为
| $ m(t)=\frac{1}{2}\lfloor u(t)+b(t)\rfloor $ | (1) |
| $ h(t)=x(t)-m(t) $ | (2) |
(3) 将h(t)作为新的数据序列,重复上述两个步骤,直到h(t)满足IMF的两个条件,就得到了第一个IMF,记为IMF1,其包含了原始数据信息的最高频率成分;
(4) 重复上述步骤,直到残余序列rn(t)是一个单调函数,即不能再分解出IMF分量为止,这时原始序列x(t)可以用所有IMF (IMF)与残余序列res.(r)之和来表达,其公式为式(3)
| $ x(t)=\sum\limits_{j=1}^n I_{\mathrm{MFj}}(t)+r_n(t) $ | (3) |
其中,j为IMF的序号;n为IMF的个数;rn(t)为残余序列,代表原始数据中的平均趋势(杨永锋和吴亚峰,2013)。
综上可以发现,EMD方法可以将由不同时间尺度或周期模式的原始时间序列数据进行分解,用简单、有规律的IMF分量来表达,以便分析判断原始序列数据的时间演变规律。
1.2.2 暴雨危险度的联合概率及重现期分析Copulas函数在多因子联合概率分析中具有显著优势,它不需要假设原始变量服从一致的边缘分布,函数形式灵活多样,建立的联合函数能更接近实际情况;能够捕捉变量之间的相依结构,所构建的函数不受变量偏态分布和异常值影响;模型描述的相依结构是一个完整分布,而不仅仅是平均状态,可以揭示变量在不同分位数上相依性强度的变化(Ji and Wan, 2021)。由于作为暴雨危险度致灾因子的暴雨日数和年最大日降雨量两指标之间可能存在线性相关关系,也有可能存在非线性或非对称关系,且各变量有可能服从不同的边缘分布,因此,尝试采用Copulas函数方法对研究区所选站点两指标数据进行联合分析,通过描述两变量之间的相依关系,构建相应的联合分布函数,综合客观地探讨两变量共同影响下的暴雨危险度时空规律。
Copulas函数构建联合分布的主要步骤为:
(1) 确定所选的时间序列数据指标的边缘分布及相应的参数;
(2) 度量所选指标变量之间的相依性(一般采用Pearson相关系数(r)、Kendall秩相关系数(τ)或Spearman相关系数(ρ)进行计算);
(3) 选择不同类型的Copulas函数并进行参数估计;
(4) 通过拟合优度检验,选择最优的Copula函数,建立联合概率分布。
Copula函数类型丰富,最常见的有椭圆簇(t Copula、Gaussian Copula等)和阿基米德簇(Frank、Clayton及Gumbel Copula等) (Nelsen,2007)。本文考虑这五种常见的Copulas函数类型,边缘分布函数的参数估计采用最大似然法(Karmakar and Simonovic, 2009),通过Kendall秩相关系数τ描述变量之间的相依性(Klein et al.,2011),结合离差平方RMSE和一般最小二乘法(Ordinary Least Squares,OLS)最小准则进行拟合优度检验,来选择最优的Copula函数类型(刘雪琴等,2012),最小OLS计算经验与理论概率之间的距离(SOLS)的公式为
| $ S_{\mathrm{OLS}}=\sqrt{\frac{1}{n} \sum\limits_{i=1}^n\left(P_{\mathrm{E} i}-P_{\mathrm{T} i}\right)^2} $ | (4) |
其中,n为样本量,PE和PT分别代表计算的经验概率和理论概率。
联合概率反映的是两变量共同作用下暴雨危险度的概率分布,五种Copulas函数模型的计算公式可参考文献(谢中华,2015)。由于最优Copula函数计算所得的联合概率是一个完整的概率分布,为进一步分析各站点联合概率大小即危险性程度,可以通过统计概率分布的特征值,即均值、分位数、极值(最大值/最小值)等指标来反映区域暴雨的危险度。
暴雨联合重现期是指每出现一次暴雨的平均时间间隔,是灾害长期预警预测的重要参考指标(姚莉等,2010)。多变量的联合重现期包括同现重现期(and)和非同现重现期(or)两种类型,其公式分别为式(5) 和式(6)。
| $ T(x, y)=\frac{L}{P(X \geqslant x \quad \text { or } \quad Y \geqslant y)}=\frac{L}{1-C\left[F_X(x), F_Y(y)\right]} $ | (5) |
| $ \begin{aligned} &T(x, y)=\frac{L}{P(X \geqslant x \quad \text { and } \quad Y \geqslant y)}= \\ &\frac{L}{1-F_X(x)-F_Y(y)+C\left[F_X(x), F_Y(y)\right]} \end{aligned} $ | (6) |
其中,T(x, y)为联合重现期,L为暴雨发生的平均间隔时间,P代表联合概率,FX(x)和FY(y)为两个单变量的边缘分布函数,C为Copula联合概率分布。
在所构建的最优Copula函数模型的基础之上,计算淮河流域整体站点平均的联合概率及重现期,以及各站点的暴雨综合危险度,并分析其时空变化特征。
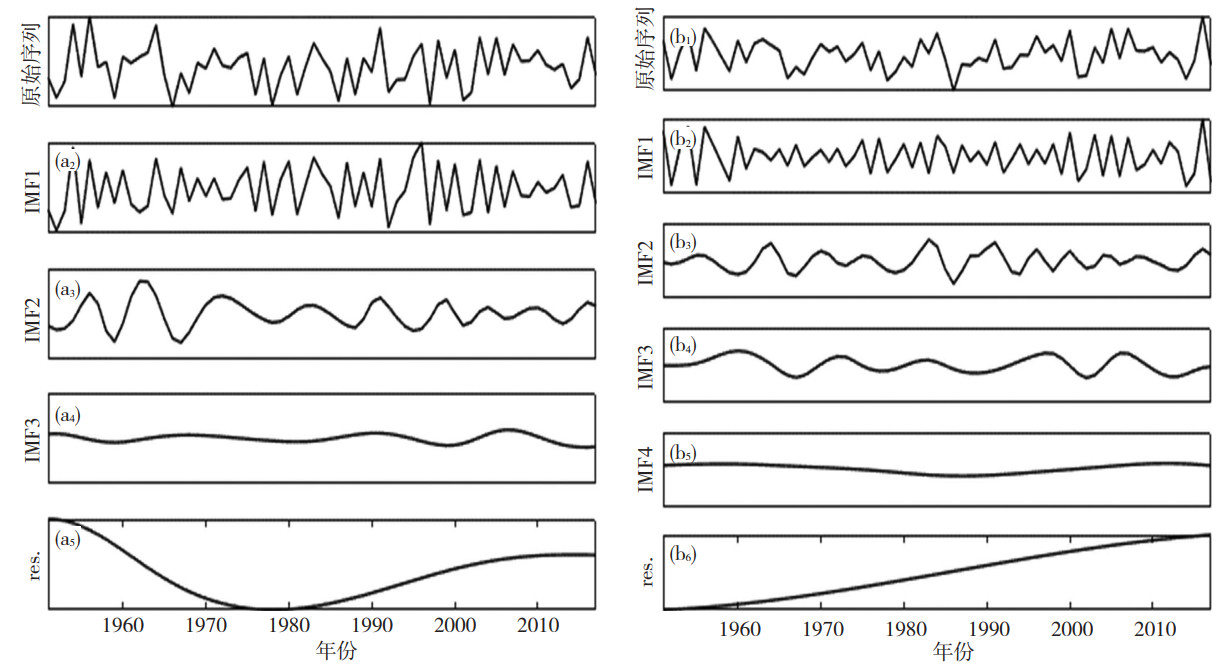
2 结果与分析 2.1 淮河流域暴雨危险度的时间变化特征 2.1.1 单指标趋势和周期的时间序列分析将所选站点的暴雨频率和强度两指标数据进行站点平均,获取反映淮河流域暴雨危险度单指标的时间序列,通过EMD方法进行分析,结果如图 2所示。从图 2可见,暴雨频率指标分成了3个分量和残余序列,而暴雨强度指标则被分解成4个分量和残余序列。两指标的IMF1与原始序列的相符程度最高,包含了最高的频率成分,但是周期和趋势情况均不易直接判读;IMF2振幅随着时间推移均呈现逐渐变小的趋势,且周期波动规律也越来越弱。残余序列(res.)反映的是原始序列的平均趋势,可以看出暴雨频率在1980年左右出现明显转折,由原来显著下降转变为显著上升趋势;暴雨强度则一直呈现出显著的上升趋势。通过进一步对1980—2017年的残余序列进行线性拟合,得到两指标的平均趋势函数分别为y=0.009 6x+2.221和y=0.078 2x + 86.266,判定系数(R) 高达0.977和0.996,说明其线性上升趋势非常显著。因此,通过对两个指标EMD结果的分析发现:淮河流域的暴雨频率的周期波动规律逐步减弱,说明流域降水系统的稳定性在下降,是可能出现极端暴雨的重要特征;暴雨频率和强度在最近40 a (1980年之后)均呈显著的线性上升趋势,说明淮河流域的暴雨频次和强度均在不断增强,特大暴雨增多。
|
图 2 年暴雨日数(a1—a5, 单位: d)和日最大降雨量(b1—b6, 单位: mm)的EMD结果 Fig. 2 EMD results of the indexes of (a1-a5) the annual rainstorm days (unit: d) and (b1-b6) the maximum daily rainfall (unit: mm) |
根据各模态极值点的位置和数量求算平均周期(即求算相邻极值点之间的平均时间长度),将由极大值点求得的平均周期与由极小值点求得的平均周期再进行平均,作为各分量的平均周期。求得暴雨频率序列IMF1—IMF3的平均周期分别为2.6 a,6.7 a,14.3 a,暴雨强度序列IMF1—IMF4的平均周期分别为2.4 a,5.5 a,9.1 a,27 a,两者对应关系较好,尤其是前两个分量序列的周期,分别约在2 a和6 a,这与已有研究中ENSO在年际变化上的信号具有一定相关性(于文金等,2016)。各分量的方差贡献率可反映其周期波动情况(表 1),两指标IMF1的方差贡献率分别为73.51%和63.48%,说明淮河流域的暴雨频率和强度的主周期均为准2 a;IMF1与IMF2的方差累计贡献率分别达到97.34% 和82.62%,说明准6 a也是淮河流域暴雨的主要周期。
|
|
表 1 年暴雨日数和日最大降雨量各分量对应的方差贡献率(单位: %) Table 1 Variance contribution rate (unit: %) corresponding to each component (IMF) of the annual rainstorm days and the maximum daily rainfall. |
将站点平均的频率和强度指标进行Copula联合概率建模,构建反映淮河流域暴雨危险度的Copula模型。采用Normal、Lognormal、Gamma、Weibull、Exponential、Extreme Value、Generalized Extreme Value、Logistic等常见的概率分布类型对两变量进行边缘分布拟合,通过对频率分布直方图的直观判断,以及Anderson-Darling (AD)检验,两变量的最优边缘分布均为一般极值分布(Generalized Extreme Value)。在此基础上,计算Kendall秩相关系数τ为0.602 7,通过了0.01的显著性水平检验,说明两变量之间存在较高的正向关系,并通过Kendall τ与Copula函数的参数之间的关系(Nelsen,2007),构建五种Copulas函数模型,结合RMSE和OLS准则进行拟合优度检验,从中选择出最优的函数类型为Gaussian Copula (表 2),相应的联合累积概率分布如图 3所示。
|
|
表 2 五种Copula函数模型的拟合优度检验结果 Table 2 Test results of fit goodness for five Copula function models. |
|
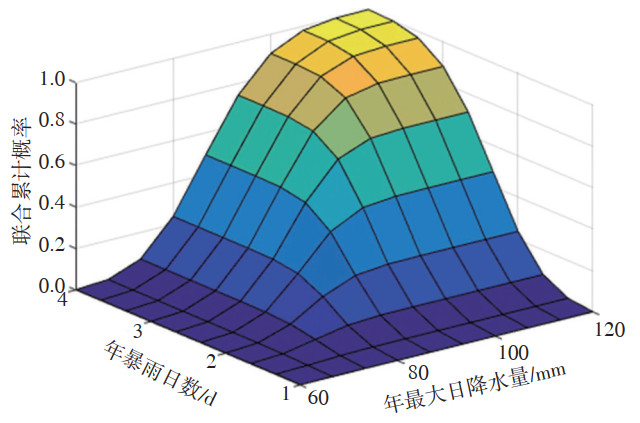
图 3 暴雨危险性联合累积概率分布图 Fig. 3 Joint cumulative probability distribution of the torrential rain hazard |
从图 3可以判断出不同频率和强度组合下的暴雨危险度的联合累积概率。从年暴雨日数指标来看,全流域平均3 d及以内的暴雨频次占总暴雨频次的90% 以上,超过3 d的以上的暴雨频次很少,并随着天数的增加暴雨频次增加缓慢;从年最大日降水量指标来看,最大日降水量小于100 mm的情况占总的暴雨强度的90% 以上,且超过100 mm后,随着最大日降水量的增加,暴雨强度增加显著变缓。
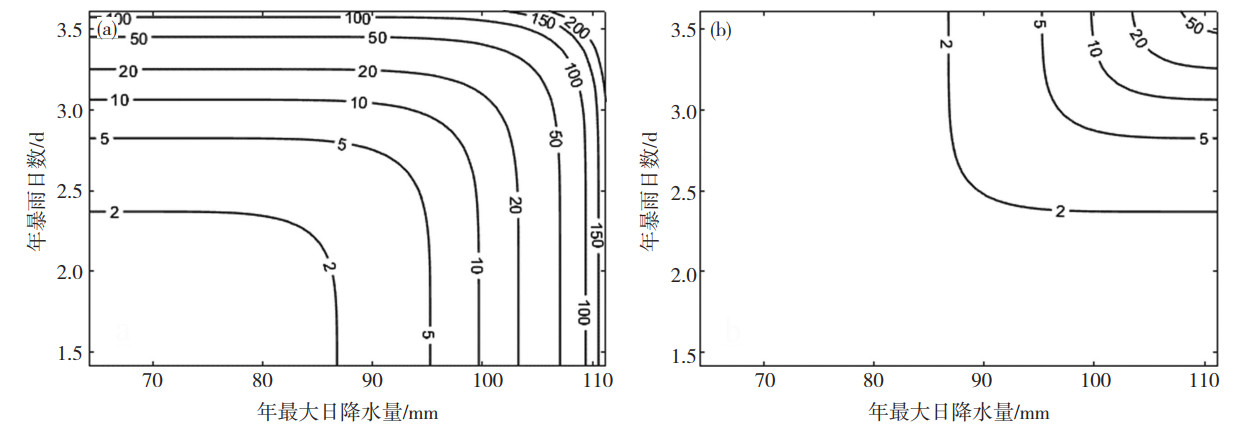
根据联合概率分布函数,进一步求算淮河流域暴雨的联合重现期(式(5)和式(6)),结果如图 4所示。可以看出,图 4a中暴雨的同现重现期(and),随着两指标值的逐步增加而增大,且增大速率变快(等值线密度增大),说明随着暴雨频次和强度的同时增加,暴雨的危险度快速增大,重现期高值出现的频率增加,即极端暴雨事件显著增多。图 4b暴雨的非同现重现期(or)也表现出与同现重现期相同的趋势,即随着两指标的增加,危险度增加速度加快,但是整体重现期值较小,说明两因素非同时作用下暴雨危险度相对较低。
|
图 4 暴雨危险性的联合同现重现期“and”(a)与联合非同现重现期“or”(b) Fig. 4 The joint return periods of the heavy rain hazard for (a)"and"and (b)"or"scenario |
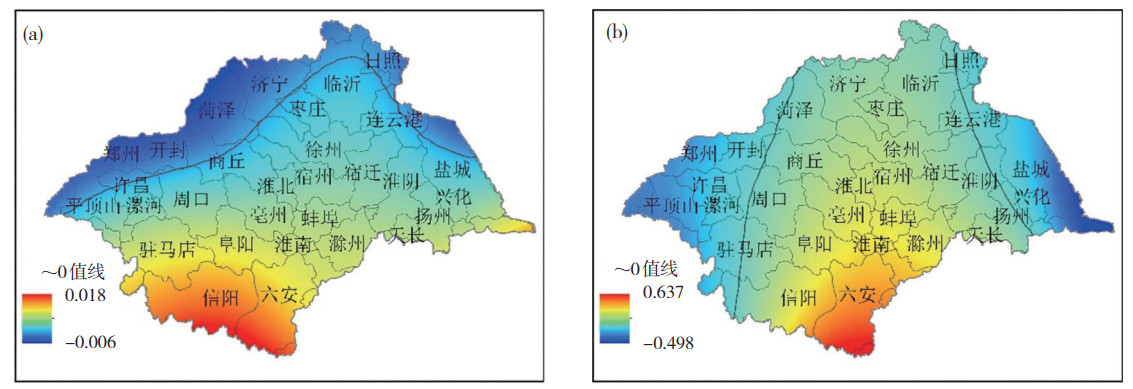
分别对流域各站点的两指标数据进行经验模态分解,并对反映平均趋势的残差项进行线性拟合,通过F检验判定线性趋势的显著性,结果显示:68个站点中频率指标和强度指标分别有52和53个站点的线性平均趋势通过了α =0.05显著性检验。将通过显著性水平检验的站点的线性趋势的回归系数通过ArcMap中的含障碍的核插值(Kernel Interpolation with Barriers,KIB)方法展布到空间上(图 5),已有研究表明KIB方法在水文和气象要素的空间插值应用中具有良好效果(Yan and Sun, 2009)。从图 5中可见,淮河流域暴雨两个指标平均变化趋势的高值空间格局表现基本一致,上升趋势最大的地区主要分布在淮河流域的西南部分,其中暴雨频次上升趋势最大的区域为河南信阳和安徽六安,暴雨强度上升趋势最大的为安徽六安。两指标对应的上升和下降趋势的区域面积比例相当,河南信阳、驻马店,安徽六安、阜阳、淮南、天长、滁州、蚌埠,江苏扬州、兴化、淮阴、宿迁、徐州,以及山东枣庄和临沂南部等地区的暴雨频次均呈增加趋势,暴雨频次下降趋势主要分布在淮河流域北部的河南郑州、开封,山东菏泽、济宁北部、日照,以及江苏盐城的东北部。暴雨强度下降趋势最大的区域分布在河南平顶山、郑州、开封、许昌,及江苏盐城等。流域内上升与下降趋势明显区域之间过渡地带的变化趋势平缓,在0值线附近波动。
|
图 5 暴雨频率(a)和强度(b)平均变化趋势的空间分布 Fig. 5 Spatial distribution of the average change trends of the heavy rain (a) frequency and (b) intensity |
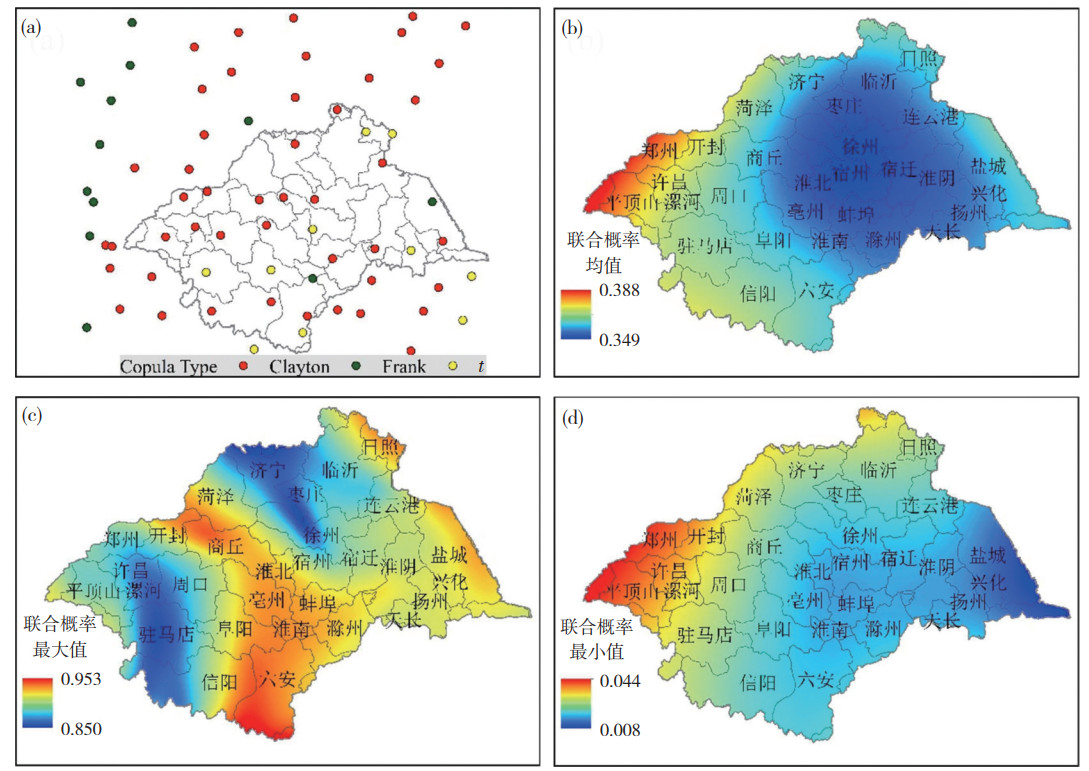
对流域各站点分别求算两指标联合概率,根据RMSE和OLS最小准则进行拟合优度检验,选取最优Copula函数模型(图 6a)并进行危险性程度的概率估计。由于联合概率计算的是各站点的整个概率分布,其特征值中的均值能够反映暴雨危险性程度的平均状态,而极值可以反映暴雨的极端状态,因此,在计算的联合概率的基础上,统计了各站点相应的特征值:均值、最小值与最大值(图 6b—d)作为暴雨综合危险度的表征,并采用KIB方法展布到整个流域。图 6a可见,流域大多数站点的暴雨危险度联合概率模型的最优Copula类型为Clayton,其次为Frank,第三为t copula,其他两种类型均没有选入。图 6b—d为联合概率的空间分布情况,可以看出三个特征值与单指标平均变化趋势的高低值(图 5)的空间分布存在显著差异。联合概率均值和最小值的空间格局基本一致,对应高值出现在流域的北部和西北地区,最低值出现在流域的东南部,并呈现由东南向西北方向逐步升高的趋势;联合概率最大值分布则比较分散,整个流域的南部及东北部均出现了最大值的高值。结合单指标平均变化趋势的空间分析,可以发现:淮河流域西北区域的部分城市,如郑州、开封、平顶山北部等城市虽然暴雨频次和强度呈现下降趋势,但是联合概率估计的暴雨综合危险度均值和最小值却很高。此外,淮河流域中南部的河南开封、商丘,安徽淮北、亳州、淮南、六安一带是联合概率最大值的高值所在,暴雨综合危险度极高。
|
图 6 各站点最优Copula类型(a)及危险性联合概率均值(b)、最大值(c)和最小值(d)空间分布 Fig. 6 (a) Optimal Copula type for each station, and the spatial distributions of the joint probability for (b) mean, (c) maximum and (d) minimum of rainstorm hazard |
本文选择年暴雨日数和年最大日降水量作为暴雨危险度的频次和强度指标,采用EMD方法分析淮河流域单指标时间序列数据的平均变化趋势及周期,采用Copulas函数方法估算暴雨的综合危险度及重现期。通过站点平均数据,分析流域暴雨危险度在单指标和两指标联合情况下的时间序列特征;再通过对各站点的数据分别计算,分析流域暴雨危险度单指标的平均变化趋势和综合危险度的空间分布规律。主要结论如下:
(1) 流域整体暴雨频次呈现先下降后上升的趋势,转折点出现在1980年左右;暴雨强度则一直呈现显著的线性上升趋势。暴雨频率和强度的主周期均为准2 a周期,6 a也是淮河流域暴雨的主要周期。
(2) 流域整体暴雨危险度的最优联合概率模型为Gaussian Copula。全流域90 % 以上的暴雨频次在3 d及以内且暴雨强度小于100 mm。超过该阈值后,暴雨频率和强度的增加显著变缓。暴雨灾害的同现重现期值和非同现重现期,均随两单指标值的增加而增大,且增大速率逐渐变快,但是同现重现期高值较高,出现极端暴雨的概率更大;而非同现重现期值相对较小,说明两因素非同时作用下的暴雨危险度相对较小。
(3) 暴雨频率和强度指标的平均变化趋势的高值空间格局表现基本一致,上升趋势最大的地区主要分布淮河流域的西南部分。两个指标上升和下降趋势的区域面积比相当,下降趋势主要分布在淮河流域北部。暴雨强度下降趋势最大的区域分布在流域的西北部,以及江苏盐城的沿海地区。
(4) 流域大多数站点的暴雨危险度联合概率模型的最优类型为Clayton Copula,综合危险度的三个特征值与单指标平均变化趋势高低值的空间分布存在显著差异。危险度的均值和最小值的空间格局基本一致,对应高值出现在流域的西北地区,最低值出现在流域的东南部,并呈现由东南向西北方向逐步升高的趋势;联合概率的最大值分布则比较分散,高值出现在流域的中南部地区。
流域西北的部分城市地区虽然暴雨频次和强度呈现下降趋势,但是暴雨综合危险度均值和最小值却很高,政府部门在作防灾减灾决策时需要充分考虑暴雨的综合危险度。流域中南部地区为暴雨危险度最大值的高值所在,气象部门在暴雨灾害的预警工作中尤其需要注意这些地区可能发生的极端暴雨事件。
本文尝试采用EMD和Copulas函数方法对暴雨危险度的单指标和综合指标开展时空特征分析。降水作为暴雨灾害风险评估中的致灾因子危险度的主要指标,除了暴雨日数和最大日降水量之外,在以后的研究中还可以增加考虑暴雨持续时间、暴雨事件频数等相关危险性指标。此外,Copula函数还可以拓展到三维甚至是高维,在未来研究中可以进一步挖掘暴雨危险性指标之间的关系,考虑更多类型的Copula函数,以期获得更为客观准确的区域暴雨危险度的时空分布规律。
董旭光, 顾伟宗, 孟祥新, 等. 2014. 山东省近50年来降水事件变化特征[J]. 地理学报, 69(5): 661-671. |
郭建平, 赵立龙. 2021. 基于前兆数据和经验模态分解的金融系统极值风险识别研究[J]. 统计与信息论坛, 36(3): 60-69. |
胡畔, 陈波, 史培军. 2021. 中国暴雨洪涝灾情时空格局及影响因素[J]. 地理学报, 76(5): 1148-1162. |
黄垭飞, 管兆勇, 蔡倩, 等. 2021. 近41年来江南地区暴雨洪涝灾害时空变化特征分析[J]. 气象学报, 79(4): 1-19. |
李宁, 顾孝天, 刘雪琴. 2013. 沙尘暴灾害致灾因子三维联合分布与重现期探索[J]. 地球科学进展, 28(4): 490-496. |
刘倪, 叶金印. 2014. 淮河流域汛期暴雨与西太平洋海温关系[J]. 沙漠与绿洲气象, 8(5): 39-43. |
刘瑞鑫, 孙建华, 陈鲍发. 2019. 华南暖区暴雨事件的筛选与分类研究[J]. 大气科学, 43(1): 119-130. |
刘雪琴, 李宁, 吉中会, 等. 2012. 基于Copulas函数的内蒙古强沙尘暴特征及其灾害性研究[J]. 干旱区研究, 29(4): 705-712. |
刘毅, 孙俊, 周国兵, 等. 2020. 近45a重庆暴雨气候变化特征分析[J]. 暴雨灾害, 39(3): 306-311. |
闵爱荣, 廖移山, 邓雯. 2016. 2008—2013年我国暴雨分布情况及变化趋势分析[J]. 暴雨灾害, 35(6): 576-584. |
潘雅婧, 王仰麟, 彭建, 等. 2012. 基于小波与R/S方法的汉江中下游流域降水量时间序列分析[J]. 地理研究, 31(5): 811-820. |
孙燕, 朱伟军. 2013. 江苏省梅汛期暴雨特征及其对长江下游水位的影响[J]. 地理科学, 33(2): 238-243. |
王晶, 薛联青, 张敏, 等. 2019. 不同降水频率下淮河流域洪涝灾害风险评估[J]. 水电能源科学, 37(9): 1-5. |
魏凤英. 2007. 现代气候统计诊断与预测技术: 第二版[M]. 北京: 气象出版社.
|
温克刚, 丁一汇. 2008. 中国气象灾害大典: 综合卷[M]. 北京: 气象出版社.
|
谢五三, 王胜. 2010. 近40 a淮河流域暴雨特征分析[J]. 暴雨灾害, 29(4): 377-380. |
谢中华. 2015. MATLAB统计分析与应用: 40个案例分析: 第2版[M]. 北京: 北京航空航天大学出版社, 219-221.
|
严志涛, 李谢辉, 刘子堂, 等. 2021. 气候变暖背景下西南四省市暴雨洪涝灾害风险变化[J]. 灾害学, 36(2): 200-207. |
杨永锋, 吴亚峰. 2013. 经验模态分解在振动分析中的应用[M]. 北京: 国防工业出版社.
|
姚莉, 赵声蓉, 赵翠光, 等. 2010. 我国中东部逐时雨强时空分布及重现期的估算[J]. 地理学报, 65(3): 293-300. |
于文金, 苏荣, 邵明阳, 等. 2016. 澜沧江流域暴雨干旱灾害与海温异常波动规律的相关性[J]. 生态学报, 36(4): 1115-1124. |
张正涛, 高超, 刘青, 等. 2014. 不同重现期下淮河流域暴雨洪涝灾害风险评价[J]. 地理研究, 33(7): 1361-1372. |
郑艳, 翟建青, 武占云, 等. 2018. 基于适应性周期的韧性城市分类评价[J]. 中国人口·资源与环境, 28(3): 31-38. |
Huang N E, Shen Z, Long S R, et al. 1998. The empirical mode decomposition and the Hilbert spectrum for non-linear and non-stationary time series analysis[J]. Proceedings of the Royal Society, 454: 903-995. |
Ji Z, Wan Y. 2021. A novel method for socioeconomic data spatialization[J]. Spatial Statistics, 43(6): 100501. |
Karmakar S, Simonovic S P. 2009. Bivariate flood frequency analysis. Part 2: a copula-based approach with mixed marginal distributions[J]. Journal of Flood Risk Management, 2(1): 32-44. |
Klein B, Schumann A H, Pahlow M. 2011. Copulas - new risk assessment methodology for dam safety. In: Schumann AH (ed) Flood Risk Assessment and Management [M]. Germany: Springer, 149-185
|
Nelsen R B. 2007. An Introduction to Copulas[M]. Germany: Springer Science & Business Media.
|
Rodriguez J C. 2007. Measuring financial contagion: A copula approach[J]. Journal of Empirical Finance, 14: 401-423. |
Shao Y, Wu J, Li M. 2017. Study on quantile estimates of extreme precipitation and their spatiotemporal consistency adjustment over the Huaihe River basin[J]. Theoretical & Applied Climatology, 127(1-2): 495-511. |
Tosunoglu F, Can I. 2016. Application of copulas for regional bivariate frequency analysis of meteorological droughts in Turkey[J]. Natural Hazards, 82(3): 1457-1477. |
Yan X, Sun X. 2009. Linear Regression Analysis: Theory and Computing[M]. Singapore: World Scientific Publishing.
|
 2022, Vol. 41
2022, Vol. 41 