引言

对流天气临近预报通常是指对某一区域雷暴及其产生的灾害性天气未来0~2 h之内发生、发展、演变和消亡的预报，在气象灾害防御中具有极其重要的地位。陈明轩等(2004)、俞小鼎等(2012)和程丛兰等(2013)对强对流临近预报方法进行了详细分析和阐述，认为目前强对流天气临近预报主要有以下两种方法：基于雷达回波的外推技术和数值天气预报技术。数值预报虽然已经在气象领域得到了广泛应用，但仍存在其自身的局限性(Weisman et al., 2010；许冠宇等，2020)，特别是在临近预报应用方面，不仅需要复杂的物理计算过程，准确率低，而且在精细化程度方面难以满足业务需求(郭瀚阳等，2019；吴剑坤等，2019；田刚等，2021)，因此，天气雷达仍然是对流天气临近预报的主要工具。目前业务上应用的临近预报方法主要是基于雷达数据的雷暴识别跟踪和自动化外推预报技术(郑永光等，2015)，主要包括：单体质心法(Dixon et al., 1993)、交叉相关法(Rinehart and Garvey, 1978)和光流法(Gibson，1950)。

大量研究表明，单体质心法由于其较大的计算量和只适用于强对流风暴的“先天性缺陷”，导致其预报准确率再难以有较大幅度的提高(徐月飞等，2011)；交叉相关法没有考虑深对流系统通常伴随较强的垂直运动，因此该方法仅适用于缓慢变化的层状云降水系统，而对快速增长或消散的强对流系统的预报效果并不理想(陈明轩等，2007；徐亚钦等，2011)；光流法可以较为准确地得到雷暴的整体运动趋势，但对于热带降水系统尤其是台风系统，光流法预报效果不如交叉相关法，其基本模型较实况仍存在不少误差，比如要求图像遵循灰度不变形假设，求解光流场时也只适用于回波运动较小的情况，对于快速移动的回波误差仍然较大(韩雷等，2008；张蕾等，2014；曹春燕等，2015)。

近年来，以深度学习模型为代表的人工智能技术在图像识别和视频领域取得了突破性进展，由于其解决复杂问题和非线性建模的突出能力，众多学者将其引入到雷达回波的临近预报中，并取得了良好的效果(许小峰，2018)。Shi等(2015)提出了卷积长短期记忆单元网络模型(Convolutional LSTM Network，ConvLSTM)，结果表明ConvLSTM优于普通的光流法；Wang等(2017)提出了PredRNN模型，并在此基础之上提出了PredRNN++模型(Wang et al., 2018)，结果显示PredRNN++效果较ConvLSTM有明显的提升；陈元昭等(2019)研究了基于生成对抗网络的临近预报方法，结果表明其对中等强度回波的预报效果较好。陈训来等(2020)利用卷积门控循环单元神经网络模型(Convolutional Gated Recurrent Unit，ConvGRU)对雷达回波进行临近预报，结果表明ConvGRU模型对强对流天气具有较好的预报效果，业务中具有广泛的应用前景；顾建峰等(2020)采用TrajGRU模型，建立了重庆地区三维雷达回波智能预报系统，并将其业务化，结果显示深度学习模型在回波演变的临近预报方面具有明显优势。

虽然基于深度学习的临近回波预报技术已经取得了令人欣喜的成果，各种模型都表现出特有的预报性能，但以往的研究大多集中在对比分析深度学习模型与传统外推预报方法预报效果的优劣性以及讨论不同天气类型下深度学习模型的适应性等方面(陈元昭等，2019；陈训来等，2020；顾建峰等，2020)，而雷达回波的发生、发展和移动是非常复杂的，同一天气型之下可以生成面积不同、强度差异显著的回波；不同天气型之下有时也可以生成面积和强度相近的回波，因此本文选取在常规数据集中表现良好、计算成本较低、内部结构差异较大且新颖的四种深度学习模型PredRNN++、MIM、CrevNet和PhyDNet(其中后两种模型是视频监测领域最新模型，尚未应用于雷达回波的外推预报)，利用武汉地区近8 a来的雷达和降水资料，通过定义回波面积指数，检验和评估深度学习模型对武汉地区不同面积雷达回波的临近预报能力，可为深度学习模型在武汉地区雷达回波临近预报的应用研究提供参考。

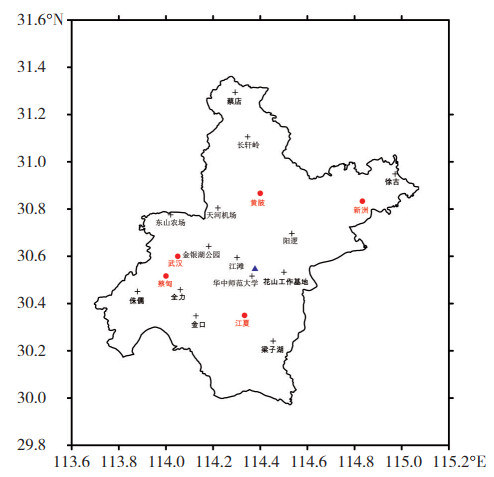
1 资料

本文使用的资料包括以下两种：(1) 2012年6月1日—2019年12月31日武汉市5个基本站和14个自动站的逐日和逐小时降水资料，气象观测站和雷达站点的空间分布如图 1所示。(2) 相应时段内湖北东部地区新一代多普勒天气雷达组合反射率因子拼图产品，其范围为覆盖湖北东部地区的以武汉雷达站为中心、边长为256 km的正方形区域，经纬度范围分别为113.098°—115.648°E，29.247°—31.797°N, 时间分辨率为6 min，空间分辨率为1 km×1 km。

首先对雷达回波数据进行了孤立噪音过滤和超折射回波抑制(吴涛等，2013)；其次为尽可能的增多训练和检验样本个数，使模型能够学习到不同类型的回波特征，同时降低样本严重失调带来的不利影响，以图 1中站点为基础，选取上述时段内间，任一站点日降水量大于等于10 mm、小时降水量大于等于0.6 mm，且组合反射率因子拼图连续3 h不间断的连续雷达回波为1个样本(如有重叠则算为1个样本)，并对其进行切片，实况输入连续的回波10张，预报输出连续回波20张，共计得到3 112个样本，考虑到各年之间天气过程的差异性较大，按照4:1的比例随机分配训练和检验样本，共计得到2 490个训练样本和622个检验样本，由于检验样本没有参与算法的训练和参数调整，因此可以客观地衡量各算法的预报能力。

2 模型和检验方法 2.1 深度学习模型简介

雷达回波临近预报的本质是时空序列的预测，在深度学习方面可以分为以卷积神经网络(Convolutional Neural Network，CNN)和循环神经网络(Recurrent Neural Network，RNN)为基础的两个大类，其中以CNN为基础的模型侧重于对空间特征的提取，而以RNN为基础的模型则更偏重于对时间特征的捕捉，且存在梯度消失的问题(Wang et al., 2018)。为了兼顾空间特征和时间信息的均衡性，因此大多数的深度学习模型将CNN和RNN结合使用，本文采用的四种模型亦如此，其中PredRNN++、MIM模型已经应用于雷达回波临近预报，而CrevNet和PhyDNet则是视频预测领域最新的模型，尚未应用于雷达回波临近预报。

2.1.1 PredRNN++模型

Shi等(2015)将RNN中传统的LSTM (Long Short-Term Memory, LSTM)中的全连接层改为卷积层，提出了ConvLSTM模型，该模型将LSTM或GRU中的记忆模块改造成CNN结构，增强了模型对空间特征的提取能力。Wang等(2017)在ConvLSTM模型的基础之上，将可以记忆的单元放置在模型的堆叠结构中，提出了PredRNN模型，为了缓解该模型中梯度容易消失的问题以及提高其对短时非线性时空特征的提取能力，引入了GHU (Gradient Highway Unit，GHU)，该结构使得梯度在第一层和第二层之间高速传递，有效抑制了梯度的消失，最终提出了PredRNN ++ 模型(Wang et al., 2018)。

2.1.2 MIM模型

Wang等(2019)为了解决PredRNN中LSTM遗忘门的饱和问题，首次将图片的信息分为平稳信息和非平稳信息两部分，提出了MIM模型，该模型分两次对图片信息进行提取，首先由MIM-N结构提取出非平稳信息，而后传递给MIM-S，MIM-S则利用门控来选择记忆或忘记非平稳信息的多少，同时通过多层模块之间相互的差分运算，使得非平稳信息缓慢降低，从而提取出各种高阶的非平稳信息，最终将所提取的平稳信息和非平稳信息相结合，进行输出与预测。

2.1.3 CrevNet模型

Yu等(2020)提出的CrevNet模型，是一种全新的嵌套了三维卷积模块的双向可逆自编码结构，其在一系列正向和反向计算过程中使得输入和特征之间建立了一对一的双向映射关系，这种关系理论上保证了在特征提取过程中不丢失信息，因而保留更多信息进行预测，明显提高了预测图片的清晰度。此外，该模型的内存和计算开销都较小，对于硬件要求不高，易于训练和调试。

2.1.4 PhyDNet模型

Vincent等(2020)提出了PhyDNet模型，该模型参考了MIM模型的基本假设，将图片信息分为已知的物理过程和未知因素(包括生消、发展等)两个部分，然后利用Phycell结构来约束模型，以ConvLSTM为主要内核来提取未知因素，以卷积过程模拟偏导，从而学习到物理过程信息，最后将物理过程信息和未知因素结合进行更好地预测。

表 1列出了应用于四种深度学习模型的主要超参数，包括图片的输入和输出长度、损失函数、迭代次数、学习率函数、初始学习率以及学习策略等。为方便对比分析各深度学习模型的预报性能，本文使用统一的损失函数、图片输入和输出的长度以及初始学习率。

2.2 检验方法

为了客观地评估各深度学习模型的预报能力，以实况回波图像为基础，先将实际回波图像和预报的回波图像格点化成单独的像素点，再逐个像素点检验预报准确率，用临界成功指数(CSI)、命中率(POD)和虚警率(FAR) 对预报结果进行量化评估，CSI (I_cs)、POD (P_od)和FAR (R_fa)的计算公式如下(陈训来等，2020)

$ {I_{{\rm{cs}}}} = \frac{{{N_A}}}{{{N_A} + {N_B} + {N_C}}} $

(1)

$ {P_{{\rm{od}}}} = \frac{{{N_A}}}{{{N_A} + {N_C}}} $

(2)

$ {R_{{\rm{fa}}}} = \frac{{{N_B}}}{{{N_A} + {N_B}}} $

(3)

其中，N_A、N_B和N_C分别表示检验范围内总的预报正确像素点数、总的空报像素点数和总的漏报像素点数。如果预报的像素点的强度与实况回波强度均大于等于K，则记该像素点预报正确；如果预报的像素点的强度大于等于K，而实况的回波强度小于K，则记该像素点空报；如果预报的像素点的强度小于K，而实况的回波强度大于等于K，则记该像素点漏报，其中K为开始检验的回波强度值。最后，统计每一张图片中的N_A、N_B和N_C (表二)。

3 回波面积指数的定义及其计算 3.1 回波面积指数的定义

为了定量衡量回波面积的大小，本文参考降水过程综合强度指数(王丽萍等，2015；洪国平，2020)中降水面积的定义方式，定义i时刻回波面积指数S_i如下

$ S_{i}=\frac{n_{i}}{N} $

(4)

其中，n_i为i时刻回波强度Z_i在某一区间的像素点数，N为总像素点数。俞小鼎等(2006)研究指出降水回波的强度一般在15 dBz以上，层状云降水回波的强度则很少超过35 dBz，产生大范围暴雨的系统在大多情况下都是积云-层状云混合结构，在大片的层状云中包含着中尺度积云强雨团，而实际业务工作中能够产生强天气的对流风暴其回波强度大多都在40 dBz以上，以鉴于此，本文定义20 Z < 40 dBz的回波为一般强度回波，Z 40 dBz的回波为强回波，分别讨论在这两种回波强度之下深度学习模型对不同面积指数回波的预报性能。

3.2 计算步骤

根据回波面积指数，对2 490个训练样本分别计算一般强度回波和强回波的回波面积指数，再将计算结果按从大到小的顺序排列，然后依次取75%分位、50%分位和25%分位的值作为大面积、较大面积、中等面积和小面积4个不同回波面积之间的分界值，分别得到了两种回波强度下4类回波面积等级的划分标准(如表 3所示)。按照表 3中给出的回波面积等级划分标准，对622个检验样本也同样进行了回波面积等级的划分，得到了不同强度回波下各回波面积等级的检验样本数(如表 4所示)，最后根据分类结果计算其具体的预报评分。

4 预报结果评分 4.1 一般强度回波下不同面积的预报评分

表 5给出了一般强度回波下各深度学习模型对不同面积回波预报的检验评分，从表中可以看出，随着回波面积的增大，深度学习模型的POD均快速上升，而FAR均大幅下降，因此CSI明显提高。从小面积回波到大面积回波，所有深度学习模型的POD和CSI增幅分别达到了40%和61.4%以上，而FAR的降幅也达到51.9%以上。以CrevNet模型为例，小面积回波时该算法的POD仅为0.45，FAR为0.29，CSI为0.38，而大面积回波时其POD增加至0.73，FAR则降低为0.12，CSI也提高到0.67，显示出深度学习模型对大面积回波良好的预报性能。

另外，从表 5中还可以看到，同一回波面积下不同深度学习模型的POD、CSI和FAR存在着一定的差异，具体表现为：在所有类型回波面积的预报中，PredRNN++模型的POD和CSI均最高，CrevNet模型最低，而MIM模型的FAR均最低。由于各深度学习模型都采用相同的输入和输出长度、损失函数以及初始学习率，因此这种差异性可能更多的来源于各模型之间结构的不同，具体言之：PredRNN++模型采用CasualLSTM级联结构来提取回波的短时非线性变化特征，并引入了GHU单元，该单元可以有效抑制梯度消失的问题，使得其能够在更深层的网络中传递信息，从而学习到更多的回波移动和发展规律，因而其POD和CSI最高(Wang et al., 2018)；CrevNet模型采用双向可逆自编码器结构，信息保留能力较强，但其采取预报图像和实况回波图像相结合的策略，导致其预报的回波位置误差较其他模型大，因而其POD和CSI最低(Yu et al., 2020)；MIM模型由MIM-N和MIM-S两部分组成，首先由MIM-N提取局部特征后，传递给MIM-S，再由MIM-S提取整体的特征，因此该模型对于整体回波形状的学习较强，因而其FAR最低(Wang et al., 2019)。

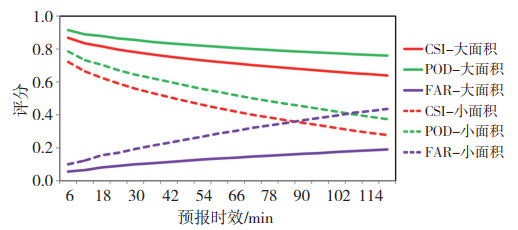
图 2给出一般强度回波下PredRNN++模型对大面积和小面积回波评分指标随预报时效的演变，可以看到无论是大面积还是小面积回波，随着预报时效的延长，POD缓慢降低、FAR缓慢增加，因而CSI缓慢降低；而这种降幅和增幅随着时效延长会逐渐变小，60 min之后曲线趋于平缓，这与前人研究结论一致(陈训来等，2020；顾建峰等，2020)，但大面积和小面积之间同一评估指标的差异却逐渐增大，例如开始时刻大面积和小面积回波之间CSI和FAR的差分别为0.146和0.044，到120 min时这种差异分别增大到了0.361和0.246，表明随着回波面积的增大，机器学习模型的预报能力显著增强，体现出机器学习模型对一般强度的大面积回波具有良好的预报性能。

4.2 强回波下不同面积的预报评分

表 6给出了强回波下各深度学习模型对不同面积回波预报的检验评分，从表中可以看出，所有深度学习模型的POD和CSI较一般强度回波时明显降低，而FAR则显著升高，说明深度学习模型对强回波的预报能力较一般强度回波明显减弱，但随着回波面积的增加，深度学习模型的预报能力仍然缓慢增强，仍以CrevNet模型为例，小面积回波时该模型的POD为0.19，FAR为0.88，CSI为0.09，而至大面积回波时其POD增加至0.23，FAR则降低为0.72，CSI也提高到0.12。此外，同一面积回波之下不同深度学习模型预报性能的差异仍然存在，其具体表现与前文所述一致，但这种差异性较一般强度回波时表现得更加微小。

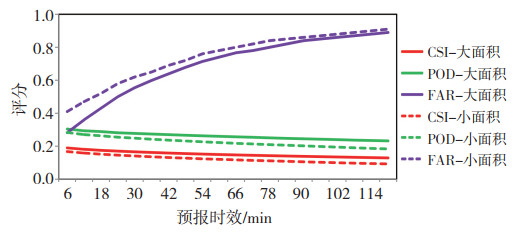
图 3给出了强回波下PredRNN++模型对大面积和小面积回波评分指标随预报时效的演变，可以看到无论是大面积还是小面积回波，随着预报时效的延长，POD缓慢降低、FAR迅速增加，因而CSI也缓慢降低；而这种降幅和增幅随着时效延长会逐渐变小，60 min之后曲线趋于平缓，但大面积和小面积之间同一评估指标的差异却无明显变化规律，例如开始时刻大面积和小面积回波之间CSI、POD和FAR的差分别为0.02、0.02和0.13，到120 min时这种差异则分别变为了0.04、0.05和0.02，表明机器学习模型对强回波面积变化的敏感性不强。

5 个例分析

2016年7月3日，受高空槽、江淮切变线和西南急流的共同作用，湖北东南部地区出现了典型的梅雨期区域性暴雨天气，暴雨以上国家站点25个，大暴雨以上13站，最大降水量为赤壁站278 mm，但各数值模式对此次过程降水落区的预报偏南，且降水强度严重偏弱。7月3日22∶24实况回波上显示（图略），武汉南部存在一强度超过45 dBz的片状回波，西北部则存在多个分散性的小面积回波块，7月3日22∶24—4日01∶18南部片状回波缓慢东移，强度变化不大，面积稍有减小，同时西北部分散性小面积回波块在东移过程中逐渐合并，回波面积增大，强度增强。

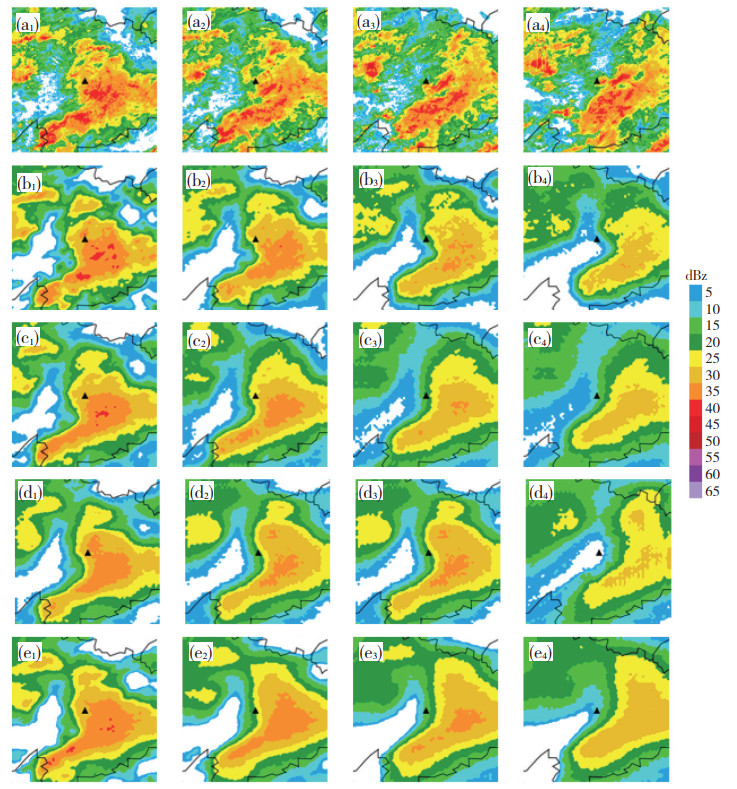
从机器学习模型预报的回波来看（图 4），各模型均较好的把握了东南部片状回波的移动，回波的整体形状以及强回波中心的位置与实况比较接近，尤其是前1 h内，与实况几乎一致，只是强回波范围较实况稍有偏大；而各模型对西北侧分散性回波块的预报均出现了一定偏差，30 min后所有模型对西北侧回波面积的估计严重不足，CrevNet和PhyDNet模型的表现较MIM和PredRNN++略好，尤其是1 h以后，MIM和PredRNN ++ 模型虚化速度加快，而CrevNet和PhyDNet模型虚化较慢，对强回波位置仍有一定反映。

为定量衡量不同深度学习模型预报的回波强度与实际回波强度之间的差异，将回波强度Z分为4个区间：10≤Z＜20 dBz、20≤Z＜30 dBz、30≤Z＜40 dBz和Z≥40 dBz，分别计算了上述各区间回波强度的频率分布(表 7)，从表中可见，对于10≤Z＜20 dBz的频率，PredRNN++、CrevNet模型表现最优，其所预报的频率与实况的频率都集中在0.268左右，而PhyDNet和MIM模型则偏高，分别达到0.341和0.358；对于20≤Z＜30 dBz的频率，所有深度学习模型的预报频率都明显偏高，其中PhyDNet模型最高，达到0.443，而MIM模型最低为0.346，最接近0.3的实际频率；而对于30 dBz以上回波的频率，所有深度学习模型的预报频率都明显偏低，其中，30≤Z＜40 dBz的频率PredRNN++模型最高为0.163，最接近实况的0.226；而对于Z≥40 dBz的频率所有深度学习模型都偏低得最显著，均不足0.01，远低于实况的0.027。总体而言，PredRNN++模型对强度在40 dBz以下的回波预报效果最好，CrevNet次之，对于40 dBz以上的回波，机器学习模型预报效果较差。

此外，各机器学习模型对于实际回波细节的把握能力较为有限，尤其是1 h以后，预报的回波强度偏弱得更加明显，回波的细节特征损失得更加严重，其原因主要有以下两个方面：一方面各模型首先都对回波图像进行离散的格点化，然后再利用各自所采用的网络结构进行空间特征的提取，这个过程中不可避免的存在信息损失，预报时效越长，信息损失得越明显，从而导致预报的回波强度较实况偏弱，回波的细节特征不显著；另一方面还可能与损失函数的设定有关，由于以均方差为损失函数平均了整幅图像的误差，使得预报的回波强度趋于平均，导致所预报的回波强度偏弱，在视觉上产生逐渐“模糊化”的过程，因而损失了大量的细节特征，这一点与Zhao等(2017)的研究结论一致。

6 结论与讨论

利用2012年6月1日—2019年12月31日武汉地区的雷达和降水资料，通过定义回波面积指数，详细分析和讨论了不同回波强度下四种深度学习模型对武汉地区不同回波面积的临近预报性能，得到以下主要结论：

(1) 随着回波强度的增加，所有深度学习模型的预报能力均迅速降低，一般强度回波的命中率和临界成功指数远高于强回波，而一般强度回波的虚警率则远低于强回波。

(2) 不论是一般强度回波还是强回波，随着面积增大各深度学习模型的POD均上升，FAR降低，因而CSI得以提高，但这种上升和降低的幅度，在一般强度回波下更显著。

(3) 无论是一般强度回波还是强回波，同一回波面积之下PredRNN++模型的POD和CSI均最高，CrevNet最低，MIM的FAR均最低，各模型之间的差异在一般强度回波时表现得更加明显，且这种差异性可能主要是由各模型之间不同的内在结构所导致。

(4) 从时间演变来看，无论何种面积、何种强度的回波，随着预报时效的增加，深度学习模型的POD缓慢降低，FAR缓慢增加，因而CSI也缓慢降低，但随着预报时效的延长，降幅和增幅都逐渐变小，60 min之后曲线趋于平缓，但不同面积之间的差异却逐渐增大。

虽然在不同强度回波之下，针对不同面积的回波，深度学习模型均表现出良好的适应性，但也存在一些问题：首先，60 min之后深度学习模型所预报的图像逐渐开始模糊，下一步拟将Dong等(2018)提出的图像梯度差(Gradient Difference Loss，GDL)引入损失函数中，进行多损失函数的加权试验，进一步提高算法对空间信息提取的能力；其次，任何深度学习模型给出的预测结果都具有一定的不确定性，这种不确定性可以分为偶然不确定性和认知不确定性两部分，偶然不确定性是由数据中的噪音产生，提高观测精度和严格的质量控制可以较好的抑制模型的偶然不确定性，认知不确定性则是由模型参数和模型结构的不确定产生，通过增加高质量的训练样本数量则可以一定程度上降低认知不确定性。也可以通过反复调整模型的超参数，最大程度的抑制模型的认知不确定性。