引言

降水在地球天气系统及全球水循环中具有重要的作用。降水的滴谱分布作为一种基本的物理参量，既可用于天气现象判断(Löffler-Mang et al., 2000；杨宁等，2018)，又可以反演降水粒子平均直径、液态含水量等物理参数，并用于微物理过程研究及联合雷达进行定量降水估测QPE等(Ryzhkov et al., 1995；Boodoo et al., 2015；张扬等，2016)。对于高原山地地区，地形的遮挡往往造成实际雷达反射率偏弱，基于地面雨滴谱的Z-R关系对山地地区的定量降水估测尤为重要(张鸿发等，1988；李德俊等，2013；赵城城等, 2014；张丰伟等，2019)。因此降水粒子谱信息在暴雨和强天气的机理和预报中的应用研究有着重要的意义。

常用的自动化降水滴谱测量设备主要采用振动法、光学法等原理进行观测(Kathiravelu et al., 2016)。JWD (Joss-Waldvogel Disdrometer)冲击式降水滴谱仪是振动法的代表，其通过测量粒子下落时其动量转换的电子脉冲信号大小，在不考虑降水粒子下落时的倾斜角及假设粒子直径和下落速度满足某些关系的条件下，能够反演得到粒子直径(Joss et al., 1967；Löffler-Mang et al., 2000)，但是该设备存在着强降水时低估小雨滴数目，测量精度受环境噪声影响、固态降水粒子测量精度较低等问题(Tokay et al., 2001)。光学法包括利用光学图像识别、光学散射原理的等方式进行的粒子测量方法。二维视频雨滴谱仪2DVD (Two-dimensional Video Disdrometer)利用光学图像识别技术，设备采用的两个线性扫描CCD (Charge Coupled Device)，可测量粒子的直径、下落速度、形状等参量，设备整体观测精度高，但因其制造成本较高、后期维护复杂，目前多用于科学研究(Kruger et al., 2002；Angulo-Martínez，2015；Park et al., 2017)；采用光学散射原理的雨滴谱主要有德国的Parsivel型雨滴谱仪、LPM型雨滴谱及我国DSG5型降水天气现象仪等，设备通过测量粒子经过观测截面时的信号振幅及时长来反演粒子直径大小及下落速度，由于其整体上的测量精度较高，购置和后期运行维护成本较低，适用于业务降水现象及微物理研究的观测需求(张昊等，2011；Wen et al., 2017；Liu et al., 2019)。

目前我国业务天气现象观测已经逐步被地面天气现象仪取代，湖北省目前已经大量布设DSG5型降水天气现象仪用于代替地面人工观测。中国气象局大气探测中心于2009、2014年分别组织了多种天气现象仪的平行对比观测研究，研究结果认为总体上我国现有天气现象仪在降水现象观测中具有良好的精度，适用于我国现阶段实际业务需求(陈冬冬等, 2010)。对于业务降水现象仪的研究，前人主要基于对降水相态、降水捕获率及降水天气现象判别准确率的研究，对于设备观测的降水粒子谱信息及其反演的微物理参量精度的研究则比较少，而这是业务降水滴谱测量信息进一步应用的基础。目前业务降水现象仪与人工观测对于大于0.1 mm·h^-1雨强的平均捕获率不低于97%，显示出与人工观测良好的一致性，但是在降水时间、降水类型方面存在一定的差异(杜波等，2017；吴宜等，2021)。而Parsivel作为一种目前国际上广泛使用的降水粒子谱测量设备，众多学者对其滴谱测量精度已经有了较多的研究，可以用于其他设备测量精度的参考(Tokay et al., 2014；Raupach et al., 2015；Park et al., 2017)。

本文利用中国气象局武汉暴雨研究所在咸宁市黑山气象观测站布设的Parsivel型激光雨滴谱仪与DSG5型业务降水现象仪观测数据，分析降水粒子谱及其反演的相关微物理参量的一致性及差异，给出设备滴谱分布反演时偏差的不确定度，为进一步扩展我国业务降水现象仪观测数据的应用提供基本参考，探索业务雨滴谱观测的粒子谱信息在降水微物理研究方面的适用性；此外，本研究还对2次雨雪转换过程中的地面人工观测与两种滴谱测量设备观测结果进行了对比分析，明确了在快速及反复雨雪转换条件下仪器与人工观测天气现象的差异。

1 资料来源与研究方法 1.1 资料来源

中国气象局武汉暴雨研究所以湖北省咸宁暴雨外场试验基地为中心，每年汛期定期开展梅雨锋暴雨野外科学试验(Fu et al., 2020；Cui et al., 2021)，这为本研究提供了良好的设备和观测基础。本文基于2018年咸宁黑山观测站8次液态降水过程开展不同滴谱观测设备反演微物理参量的对比研究，基于2次雨夹雪过程开展不同观测设备对雨雪等降水天气现象的识别差异研究(表 1)。同址观测设备包括德国OTT Hy⁃ dromet公司生产的第二代产品Parsivel2型激光雨滴谱仪(以下简称Parsivel)、华云升达DSG5型降水天气现象仪(以下简称DSG5)、DZZ5型地面自动翻斗式雨量计(以下简称AWS)及人工观测的天气现象数据(以下简称人工观测)。DSG5、AWS与人工观测均位于咸宁黑山观测场内，Parsivel则位于观测场外，距离DSG5及AWS约20 m。

Parsivel激光雨滴谱仪采用精度更高的传感器，激光带的均匀性也得到了提高，使得其观测降水粒子的精度相对于上代产品有一定的提高。当降水粒子经过采样区时，测量下落粒子通过激光束时信号衰减振幅可以反演出粒子直径，信号变化的持续时间反演出粒子下落速度。Parsivel发射的水平激光束波长为650 nm，采样区面积为54 cm² (180 mm×30 mm)，可测量范围内的直径和速度各分为32档(表 2)，直径级别的宽度从0.125~3 mm不等，速度级别宽度则由0.1~ 2.8 m·s^-1不等。由于前两个直径级别内的粒子信噪比较低，Parsivel在数据输出时将前两档直径内的粒子数据进行了剔除(Tokay et al., 2014)，所以其最小可测粒子直径为0.25 mm。考虑到液态降水粒子的形变，对于直径1 mm以下的粒子被认为是球形，1~5 mm之间的粒子被认为是扁率为1~0.7线性变化的扁球体，大于5 mm的粒子则被认为是扁率为0.7的球体(Battaglia et al., 2010)。设备顶部配有防溅罩，能够有效减少降水粒子破碎飞溅引起的观测误差。

DSG5型降水现象仪由华云升达研发，其顶部同样配有防溅罩以减少降水粒子破碎对观测的影响。设备观测的粒子分为32个直径与32个速度共计1024个级别，其直径和速度档分级与Parsivel的分级标准相同。DSG5根据设备自身特点保留了前两档上的数据，所以其最小可测直径为0.125 mm。在降水天气现象输出方面，Parsivel以WMO规定的SYNOP 4680表输出天气现象代码，而DSG5型降水现象仪则输出适合我国目前业务运行实际需求的雨、雨夹雪、阵性雨夹雪、霰等共计11类天气现象。

翻斗式雨量计为常规地面业务降水观测设备，其最小可测累积雨量为0.1 mm。天气现象地面人工观测依据《地面气象观测数据文件和记录簿表格式》中的要求，一般站在每天08∶00—20∶00时(北京时，下同) 记录雨、雪等天气现象及其起止时间等。虽然人工观测存在一些缺点，例如主观性强，对快速变化的天气现象观测不全面等，但是人工观测仍然是目前最可靠的降水现象观测方法之一。

Parsivel及DSG5都是通过测量降水粒子直径和下落速度来识别天气现象以及反演微物理参量，两种降水滴谱观测设备测量原理相同，但由于实际硬件以及算法上的差异，仍然会造成两者观测结果的差异。Parsivel目前已经在世界范围内广泛使用，其优缺点很多学者已经进行了充分的讨论，所以在本研究中进行对比时，以Parsivel作为参考来进行后续的分析讨论。同时，在进行地面降水及降水现象对比时则以地面业务自动站和人工观测作为基准进行分析。

1.2 数据质控

在Parsivel与DSG5两种滴谱观测设备液态降水过程微物理参量反演前，需要进行一定的数据质量控制处理。自然降水中很少有超过8 mm的雨滴存在，个别超过8 mm的粒子往往是雨滴重叠所产生的，所以首先需要剔除直径大于8 mm的降水粒子。此外由于降水粒子溅射、大风等对观测的影响(Atlas et al., 1973)，会观测到一些速度较大的小粒子以及速度较小的大粒子，研究时需要将每分钟观测到的降水粒子数据根据理论速度-直径关系式进行过滤，以剔除速度- 直径理论值之外± 50 %的粒子；再次对于分钟样本数据，当其雨强RR < 0.1 mm·h^-1或者设备观测截面记录的粒子数小于10个，可以认为是噪声的影响，也将其进行剔除(Kruger et al., 2002; Wen et al., 2016; Angulo-Martínez et al., 2018)。最后采用有效观测截面代替设备的物理观测截面，以减少设备边界效应对参量反演的影响(Tokay et al., 2013)。经过上述数据质控后重新计算相关微物理参量，8次液态降水过程总计得到Parsivel和DSG5匹配分钟样本数共计1 503对。

1.3 微物理参量计算

地面降水滴谱分布一般可以用双参数M-P分布或者三参数Gamma分布表示。一般认为三参数Gamma分布能够更好表示地面实际降水滴谱分布情况(Kozu et al., 1991; Zhang et al., 2001; Smith P L, 2003; Brandes et al., 2004)。Gamma分布可以表示为

$ N(D)=N_{0} D^{\mu} e^{-\lambda D} $

(1)

其中D (单位: mm)是粒子等效体积直径，N(D) (单位: mm^-1·m^-3)是单位等效直径D内的粒子数浓度。N₀ (单位：mm^-1-μ·m^-3)、λ (单位: mm^-1)、μ分别为截距、斜率及形状参数。M-P分布可以看做是Gamma分布在形状因子μ = 0时的特殊情况。

在计算滴谱相关参量时通常采用阶矩法，该方法的优点在于降水微物理参量与各个阶矩量有一定的对应关系，例如0阶矩为雨滴谱总数浓度N_t，6阶矩正比于雷达反射率因子Z等，n阶矩定义如下

$ M_{n}=\int_{D_{\min }}^{D_{\max }} D^{n} N(D) \mathrm{d} D $

(2)

因此降水相关物理量雷达反射率因子Z (单位: mm⁶·m^-3)、液态水含量LWC(单位: g·cm^-3，简称L_wc)、总数浓度N_t (单位: m^-3)及雨强RR(单位: mm·h^-1，简称R_R)可以用下式表示

$ Z=\sum\limits_{i=1}^{L} D_{i}^{6} N\left(D_{i}\right) \Delta D_{i}=M_{6} $

(3)

$ L_{\mathrm{W C}}=\frac{\pi}{6000} \sum\limits_{i=1}^{L} D_{i}^{3} N\left(D_{i}\right) \Delta D_{i}=\frac{\pi}{6000} M_{3} $

(4)

$ N_{t}=\sum\limits_{i=1}^{L} N\left(D_{i}\right) \Delta D_{i}=M_{0} $

(5)

$ R_{\mathrm{R}}=\frac{6 \pi}{10^{4}} \sum\limits_{i=1}^{L} D_{i}^{3} V\left(D_{i}\right) N\left(D_{i}\right) \Delta D_{i} $

(6)

式中L是粒子直径分级总个数，D_i是粒子分级中第i个分级的等效体积直径，ΔD_i是第i个分级的等效直径宽度。V(D_i) (单位: m·s^-1)是等效直径D_i时的粒子下落速度。

由于N₀不是一个独立且具有明确物理含义的变量，一般可以采用标准化截距参数N_w (单位: m^-3·mm^-1) 进行表示，其被定义为与N₀含义类似，但是具有与被测量滴谱分布具有相同的L_WC和质量加权平均直径D_m的参量(Testud, 2001; Bringi et al., 2003)。因此降水粒子相关微物理量D_m、N_w及σ_M (D_m标准差)定义如下

$ D_{\mathrm{m}}=\frac{M_{4}}{M_{3}} $

(7)

$ N_{\mathrm{w}}=\frac{4^{4}}{\pi \rho_{\mathrm{w}}}\left(\frac{10^{3} L_{\mathrm{WC}}}{D_{\mathrm{m}}^{4}}\right) $

(8)

$ \sigma_{\mathrm{M}}=\frac{D_{\mathrm{m}}}{(4+\mu)^{1 / 2}} $

(9)

其中ρ_w为水的密度(1.0 g·cm^-3)。

DSG5与Parsivel对比分析时采用相对偏差(B_ias)和绝对偏(A_bias)，其计算公式如下：

$ B_{\text {ias }}= \frac{\sum\limits_{i=1}^{n}\left(x_{i}-y_{i}\right)}{\sum\limits_{i=1}^{n} \frac{\left(x_{i}+y_{i}\right)}{2}} \times 100 \% $

(10)

$ A_{\text {bias }}= \frac{\sum\limits_{i=1}^{n}\left|x_{i}-y_{i}\right|}{\sum\limits_{i=1}^{n} \frac{\left(x_{i}+y_{i}\right)}{2}} \times 100 \% $

(11)

其中n是样本个数，x_i、y_i分别代表不同设备观测到的物理量。

2 结果与分析 2.1 累积降水对比

降水是地面观测的重要物理参量，雨滴谱观测反演的降水精度也可以从侧面反映出其滴谱的测量精度。8次降雨过程AWS、Parsivel和DSG5的小时累计降水量及两种滴谱设备反演的分钟雨强对比如图 1 a—d所示。8次降水过程中AWS、Parsivel和DSG5分别观测到的降水小时数为59、64和55 h。AWS观测到261.8 mm降水，为三种设备最大值；Parsivel观测到的降水小时数最多，共记录251.5 mm累积降水量，相对于AWS偏小约4.0 %，绝对偏差为10.0 %，两者观测的降水一致性较高(图 1a)。DSG5记录的累积降水量仅为220.4 mm，其降水小时数及降水量都是三者中最少的，其相对于AWS低估约17.2 %，绝对偏差为21.4 %，尤其是对于小时累积10 mm以下的降水，DSG5有比较明显的低估(图 1b)。与Parsivel的小时累计雨量观测结果相比，DSG5偏小约13.2 %，绝对偏差为20.7 %(图 1c)。两种滴谱设备观测的累积降水都小于地面自动站AWS的观测。为了进一步对比Parsivel和DSG5分钟降水观测一致性，其分钟雨强散点图如图 1d所示。DSG5相对于Parsivel偏小约12.5 %，雨强较小时有较为明显的低估(尤其是分钟雨强小于10 mm·h^-1)，随着雨强的增大，两者的一致性逐渐提高。

整体来看，两种滴谱测量设备Parsivel与DSG5观测到的累积降水均小于地面AWS，但是Parsivel观测到的小时降水相对于DSG5降水精度更高，偏差较小。DSG5则相对于Parsivel及AWS都有一定的偏小。而这种偏小主要集中在雨强较小时，随着雨强的增加，DSG5与其他设备观测的一致性也随之提高。

2.2 微物理参量对比

将上述Parsivel和DSG5匹配的1 503个分钟降水样本反演的粒子总数浓度N_t、质量加权平均直径D_m等微物理参量进行统计(表 3)。总体上看，Parsivel探测的粒子数相对较多、粒子直径相对小。Parsivel粒子总数浓度N_t是DSG5的3倍，Parsivel归一化阶矩参数log₁₀N_w为3.60也高于DSG5反演结果，而Parsivel的质量加权平均直径D_m为1.56 mm则略微偏小于DSG5的1.69 mm；由两设备的D_m的标准差σ_M相近可以推测两者反演的D_m的谱宽几乎相同。Parsivel液态水含量LWC则略大于DSG5，Parsivel平均雨强RR为10.31 mm·h^-1略大于DSG5，Parsivel观测反演的雷达反射率较DSG5结果偏大约2.7 dBz。可以看出Parsivel观测到的降水粒子平均尺寸略小于DSG5，但是数浓度更高，而且从雷达反射率上看，Parsivel的平均反射率要明显大于DSG5的观测结果。

为了进一步表明两种设备D_m、log₁₀N_w、LWC及Z的分布差异，图 2给出了其概率密度PDF (Probability Density Function)和累积概率密度CDF (Cumulative Distribution Function)。两种设备D_m的PDF分布形态相似，尽管Parsivel探测粒子直径分布峰值位于1.3 mm、而DSG5探测的D_m峰值则位于1.1 mm。对于D_m小于2.3 mm的粒子Parsivel所占比例CDF为0.95高于DSG5的0.85，Parsivel观测到的小粒子直径的比例较高(图 2a)。而两种设备log₁₀N_w的分布则和D_m相反，DSG5的峰值出现在3.1，Parsivel则出现在3.9，Parsivel观测到的高粒子数浓度的比例较高，其分布相对于DSG5整体分布偏向右侧，也就是说两种观测设备中DSG5相对于Parsivel观测到直径较大粒子的比例高，但是其观测的高粒子数浓度样本的比例则明显偏低，在平均值上表现为DSG5的D_m平均值更大，但是总数浓度N_t及归一化阶矩log₁₀N_w则明显偏低(图 2(b))。DSG5观测到的LWC小于0.02 g·m^-3及大于1.58 g·m^-3样本比例明显大于Parsivel观测结果，其平均值也略小于Parsivel，这与log₁₀N_w的观测结果一致(图 2c)。从雷达反射率PDF及CDF分布上来看，Parsivel 20~45 dBz反射率比例高于DSG5，而DSG5小于20 dBz回波所占比例明显大于Parsivel，两者对于大于45 dBz的反射率相差不大，DSG5仅略高一点(图 2d)。整体上来说，Parsivel虽然测量的平均直径相对于DSG5小，但是粒子数浓度却要高的多，这反而造成了两者的反射率PDF分布差距并不如浓度分布那么明显。

Parsivel和DSG5匹配的1 503个分钟降水样本包括了不同强度的降水，图 3是D_m-RR及N_w-RR散点及拟合图，可以看出两个设备所探测粒子的质量加权平均直径D_m变化趋势较为一致，两者都随着雨强的增大而增大，Parsivel的拟合结果始终位于DSG5的下方，在同等雨强情况下Parsivel的观测D_m总体小于DSG5的观测（图 3a）；N_w随着雨强的增大，其增大幅度较为平缓（图 3b），Parsivel与DSG5两者拟合N_w-RR曲线几乎平行，在同等雨强情况下Parsivel的观测N_w总体大于DSG5的观测。综合图 3分析，两种设备的观测结果都显示：雨强的增大主要来源于降水粒子平均尺寸的增大，粒子数浓度的增长在雨强增大到一定程度后增幅较为缓慢，对雨强增长贡献较小。

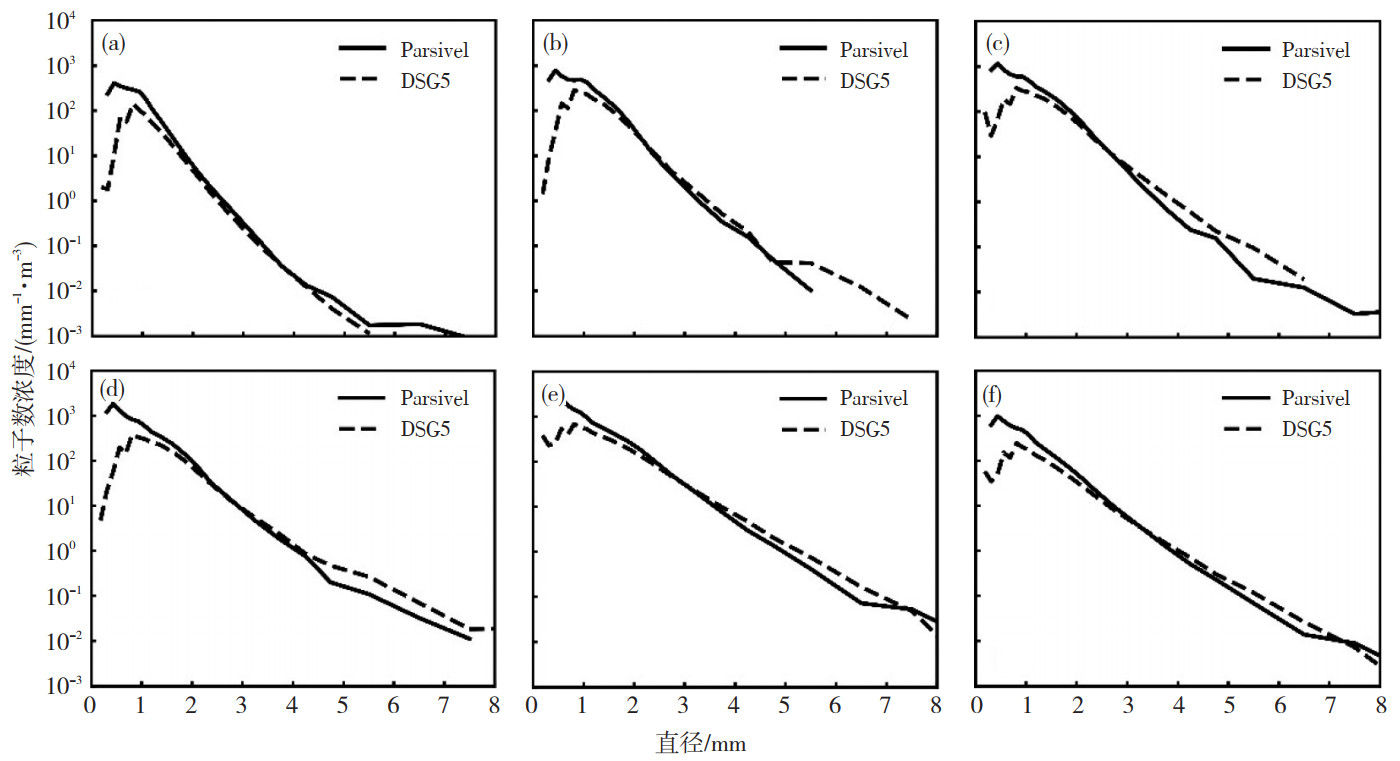
为了进一步明确在不同雨强下两种设备观测的平均滴谱差异，将1 503个样本按照0.1≤RR＜5.0、5.0≤RR＜10.0、10.0≤RR＜15.0、15.0≤RR＜20.0、RR≥20.0 mm·h^-1及整体样本的降水等级进行平均滴谱分布计算(图 4)。随着雨强的增大，观测到的粒子数浓度变大，粒子直径也随着变大。相对于Parsivel，在所有等级降水情况下，DSG5对于小(大)粒子的观测数浓度低(高)估，这种差异导致两种观测反演的平均雷达反射率相差大约2.7 dBz (表 4)，与Tokay (2014)对于Parsivel一代与二代设备的对比结论3.4 dBz类似，Tokay将产生这种现象的原因归结于激光器件的均一性及传感器精度的差异。对于5≤RR≤20 mm·h^-1雨强降水，对于2 mm以下部分的小粒子，Parsivel观测数浓度高于DSG5观测的数浓度，对于直径2~3 mm区间粒子两种观测数浓度两者趋于一致(图 4b—c)。在雨强为10≤RR≤20 mm·h^-1的情况下，Parsivel对于直径大于4 mm以上大粒端粒子数浓度观测低于DSG5 (图 4c—d)，对于RR≥20 mm·h^-1，Parsivel对小于(大于)粒子直径3 mm的粒子的数浓度观测高于(低于)DSG5的观测。对于RR≤20 mm·h^-1降水观测，两种设备的滴谱都呈现一个下凹的形状，即在大粒子区间会产生粒子数的先减后增的波动，这种原因现象产生的原因可能一方面受降水微物理机制的影响，大粒子蒸发效应强于其相互间的碰撞破碎效应；另一方面设备观测噪声等也是造成这个现象的原因(Sauvageot et al., 1995；Atlas et al., 2000；Tokay et al., 2010)。

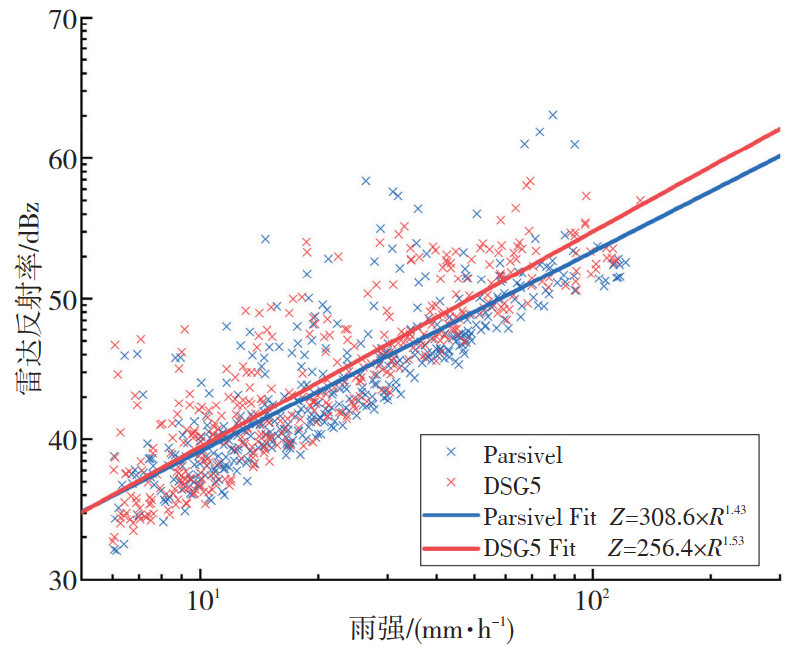
为进一步探究两种滴谱设备观测差异对反演参量的影响，分析了基于两种设备的Z-R关系差异。关注中等以上雨强，选取分钟雨强RR≥6 mm·h^-1的样本，采用最小二乘法分别进行Z-R关系拟合，Parsivel及DSG5拟合结果分别为

$ Z=308.6 \times R^{1.43} $

(12)

$ Z=256.4 \times R^{1.53} $

(13)

对于同等雨强，相比于Parsivel，DSG5观测反演的Z偏大，且随着雨强的增大，两者的偏差逐渐增大(图 5)。在图 2d中也可以看出，对于大于50 dBz的反射率，DSG5比例比Parsivel高。对于50 dBz的反射率，基于(12)、(13)中各自拟合的Z-R关系，DSG5大约高估15.9%的降水。基于DSG5观测拟合的Z-R关系相对于Parsivel会造成Z高估，虽然DSG5观测到的中小粒子数浓度低估会带来小粒子端反射率的低估，但是从图 4中可以看出，DSG5观测到的大粒子数浓度较高，而且雷达反射率与直径的6次方成正比，这可能造成在雨强较大时Z值偏大，从而造成Z-R关系整体高估，虽然从整体上看基于DSG5观测反演的平均Z低于Parsivel(表 3)。

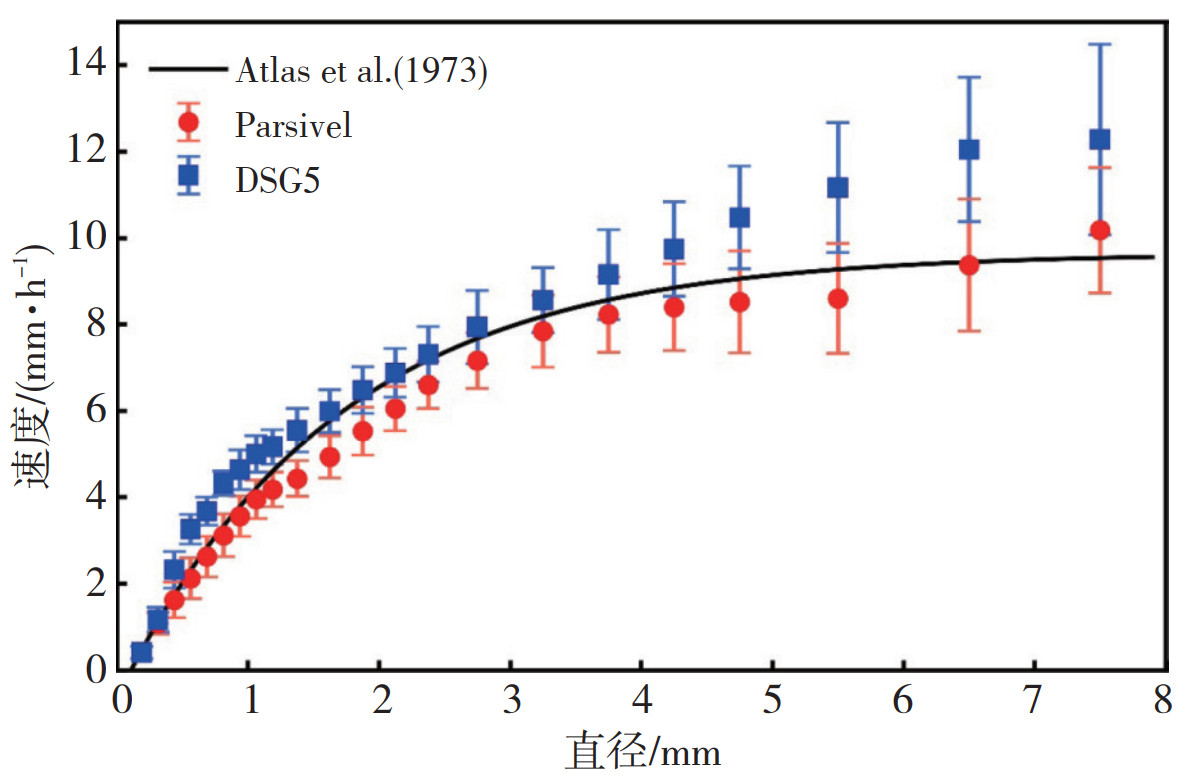
随着对降水的物理机制研究的深入，降水粒子的下落速度越来越受人关注(Gunn et al., 1949；Beard K V，1976；Löffler-Mang et al., 2000)。研究表明即使在有风的情况下雨滴的轨迹可能会偏离垂直方向，但对降雨粒子平均下落速度与理论最终下落速度非常接近(Tokay et al., 2014)。图 6是Parsivel和DSG5两种雨滴谱仪8次降雨过程平均直径-落速图，同时也采用Atlas等(1973)所统计的粒子直径-下落速度关系作为理论值计算了对应直径分级的平均速度和标准差。可以看出，对于4 mm以下直径的降水粒子，两种设备观测的下落速度与理论值都比较接近。Parsivel几乎在所有直径上下落速度都略低于理论值，但是与理论值最为接近，而DSG5则显示相反的趋势，几乎在所有的直径上对应的理论速度都略大于理论值，尤其是对于大于4 mm直径的粒子，其测量的粒子下落速度明显大于理论值。具体来说Parsivel直径-下落速度偏差随着直径经历了先增大再减小最后增大变为正偏差的过程，偏差先从直径0.3 mm时的-3.0 %随着直径的增长变大，在1.6 mm时达到最大偏差-14.5 %，之后，随着直径的增大偏差又逐渐减小，在6.5 mm时达到-0.8 %，之后偏差转为正偏差。这个结果和前人研究结果一致(Tokay et al., 2013; Wen et al., 2017)，考虑到该设备测量到的粒子直径和下落速度是归一化到不同的直径分级中去的，所以这个误差在可接受范围之内(Krajewski et al., 2006)。DSG5直径-下落速度偏差也随着直径经历了先增大再减小最后增大过程。不同的是，在1.18 mm以下直径，落速偏差有一个明显的增大后再减小的过程，在0.56 mm时达到41.7%，在2.3 mm时达到最小1.8%。在中段粒子1.8~3.75 mm与理论值误差很小。直径大于4 mm的粒子，其与理论速度的差异较为明显，而且有明显偏差随着直径增大的趋势，但是这个结果仍然好于学者对Parsivel一代产品的评估结果(Wen et al., 2017)。DSG5在1.5 mm前的速度增大现象，这可能是降水粒子破碎飞溅导致尺寸较的粒子的下落速度小于理论值(Tokay et al., 2013)。国外学者的研究表明，Parsivel产品1~3 mm直径粒子下落速度相比理论值的低估可能是源于厂家软件上的问题，这种现象在本研究中同样存在(Tokay et al., 2014；Angulo-Martínez et al., 2018)。而DSG5对于直径大于4 mm降水粒子下落速度的高估则可能造成该直径范围内测量的粒子数浓度的高估(图 4)，从而对微物理参量的反演产生一定的影响。相对于其他微物理参量，雷达反射率由于和粒子直径的6次方成正比，该部分高估对Z-R关系的拟合也将产生一定的影响，尤其是在地面降水较强时，对于其他的微物理参量则因其计算时与直径和粒子数浓度关系的不同而有所差异。对于大粒子，Parsivel探测下落速度小于理论值，DSG5探测的下落速度大于理论值这种现象，值得在今后在资料的应用中注意。

2.3 降水天气现象观测对比

人工天气现象观测依据地面业务观测规范《地面气象观测数据文件和记录簿表格式》中的要求，主要记录包括降水现象、地面凝结现象、视程障碍现象、雷电现象和其他现象共计34种。业务降水现象仪仅限于视程障碍现象和降水现象的自动化观测，包括雨、阵雨、毛毛雨、雪、阵雪、雨夹雪、阵性雨夹雪、霰、米雪、冰粒、冰雹共计11种，而Parsivel则按照WMO规定的SYNOP 4680表中规定的降水类型代码进行记录。12月7号以及28号两次过程均为从降雨转换为雨夹雪，最后转换为降雪相态的降水过程。由于人工和两种滴谱设备记录的降水天气现象种类并不完全一致，所以根据两次天气过程中的实际降水情况，将天气现象主要分毛毛雨(50、51、52、53、57、58)、雨(60、61、62、67)、雨夹雪(68)、雪(70、71、72、85)、霰(87、88)五类。

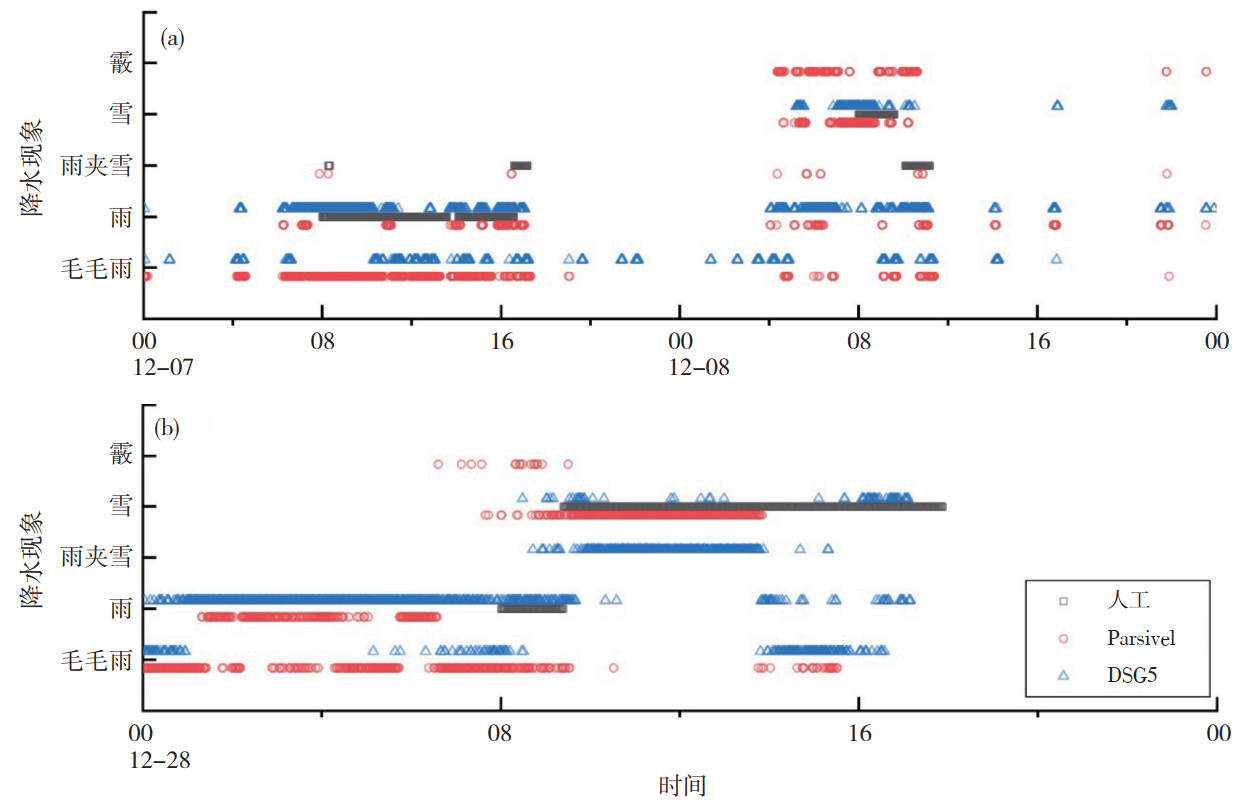
12月7日降水过程较为复杂，包含了降雨、降雪以及多次雨雪快速转换过程。从两种滴谱仪识别的天气现象上来看，整个转换过程存在较为频繁的雨和雨夹雪转换(图 7a)。7日08时前Parsivel与DSG5观测到毛毛雨和雨，人工此时未开始观测。08∶00—17∶00人工观测的降水现象以降雨为主，零星包含雨夹雪，而Parsivel则没有观测到两次零星的雨夹雪过程，其观测以降雨为主，毛毛雨次之，而DSG5则相反以毛毛雨为主，降雨次之。DSG5也观测到了两次零星的雨夹雪过程，时间上略超前于人工观测发生时间。8日08∶00之前两个滴谱设备都观测到了降雪，08∶00之后人工观测到雪及雨夹雪，Parsivel则观测到了雪、雨及毛毛雨，没有观测到雨夹雪，DSG5除上述天气现象外还观测到了霰，对人工观测到的雨夹雪也有一定的反应，但是观测时长更短。

12月28—29日过程也是一次雨雪转换过程，该次降水过程中相态转换过程较为平稳(图 7b)。08∶00地面观测到降雨，09∶24人工观测到降雪并持续到17∶52，而Parsivel则在07∶39就观测到的首次零星的降雪，但是仍然以毛毛雨和雨为主，基本上与人工观测一致，而09∶33后则观测到以雨夹雪为主，降雪次之，而雨夹雪是人工观测记录中没有的。DSG5在09∶30前观测基本上与人工一致，但是有零星的霰，09∶30以后则以降雪为主。此外从13∶50之后，两种滴谱设备都记录了零星的雨及毛毛雨，但是人工观测明显忽略了这一点，全部记为降雪。在雨雪转换的开始时间，两种滴谱设备观测到的转换时间都略早于人工观测，同时对于降雪中间出现的零星不同相态的降水也可以进行良好的记录，天气现象的结束时间也略早于人工观测。这可能是因为人工在确认降水相态转换并进行记录时，可能由于观测原因可能会产生延迟(吴宜等, 2021)。

从实际数据来看，人工观测的降水类型少于降水现象仪及Parsivel的观测，而Parsivel观测的降水现象最多。两种设备都出现了毛毛雨和雨频繁切换的问题，这个可能在未来的算法中综合台站湿度、温度等参量进行综合判别(杨宁等, 2018)。两种滴谱设备测量的天气现象相对于人工观测都有一定的提前，这可能是人工降水现象观测存在不足，无法高时间分辨率的识别实时天气现象，对快速转换的天气现象记录存在一定的困难。从整个降水相态的识别记录上来看，DSG5记录的降水现象则更接近于人工地面记录的结果，两者降水类型更为接近。在两个个例中，DSG5都识别出了霰，但是人工观测和Parsivel却没有观测到相应的降水现象，这可能和设备的识别算法有关，后续仍需厂家进行改进。

3 结论与讨论

通过Parsivel、业务雨滴谱仪DSG5以及地面自动站AWS雨量对比，以及Parsivel和DSG5反演物理特征参量的对比分析表明：

(1) Parsivel观测到的小时降水与地面自动站AWS观测到的降水量一致性较高，偏差较小，而DSG5则相对于Parsivel及AWS都有一定的偏小。而这种偏小主要集中在雨强较小时，随着雨强的增加，DSG5与其他设备观测的一致性也随着提高

(2) 从1 503个样本的分布看，Parsivel探测的粒子数相对多、粒子直径相对小；RR、LWC和Z三种物理参量的反演值，Parsivel的较DSG5高。Parsivel的观测D_m (N_w)总体小(大)于DSG5的观测。对于RR≥20 mm·h^-1的样本，Parsivel对于粒子直径小于(大于) 3 mm粒子数浓度高于(低于)DSG5的观测。

(3) 对于4 mm以下直径的降水粒子，两种观测的下落速度与理论值都比较接近。对于大于4 mm直径的粒子，Parsivel的观测的落速都略低于理论值，DSG5的观测的粒子落速明显大于理论值。

(4) DSG5业务降水现象仪对降水现象有着良好的观测，相比于Parsivel，在降水相态转换过程中其天气现象与人工观测的降水类型一致性更好，由于设备相对于人工观测更高的时间分辨率，可对降水相态的转变和结束时刻记录的更早更精确。

国内目前已经大范围布设了降水现象仪观测网，充分利用其观测的滴谱信息进行大范围降水过程的微物理研究、雷达Z-R关系拟合等有良好的应用前景。了解不同类型滴谱的观测特性对于后期资料的应用显得基础且重要。下一步将基于雨滴谱观测，对降水粒子下降速度与滴谱的关系特点做更深入分析研究，并将粒子滴谱和粒子下降速度等观测特性应用于模式物理方案改进中。