引言

定量降水预报(Quantitative Precipitation Forecasts，QPF)由于影响其时空分布的因素太多，一直被认为是天气预报最困难的挑战之一(Applequist et al., 2002)。数值模式的降水预报产品是定量降水预报最重要的技术支撑。比如：欧洲中期天气预报中心(European Centre for Medium-range Weather Forecasts，ECMWF)全球模式通过不断提升空间分辨率、改进数据同化能力、完善数值计算方法和次网格物理过程的参数化方案，其降水预报技巧在不断提高(Forbes and Tompkins, 2011；Forbes et al., 2015；Malardel et al., 2016)。新一代华东区域模式(WARMS 2.0)作为目前华东区域气象中心主要的区域数值预报业务模式系统，其对降水的预报性能相比原业务模式得到了明显改善，对降水事件发生的捕捉能力也得到了进一步增强(徐同等，2016；张萍萍等，2018)。然而不同模式的降水预报也存在各自优缺点。大量检验结果表明ECMWF对大尺度天气的预报效果整体上优于其他模式(张宁娜等，2012；肖红茹等，2013；刘静等，2014；任宏昌，2018；尹姗等，2020)，但对局地性、对流性降水过程的预报能力明显不足(辛辰和漆梁波，2018；王万筠等，2018)。党英娜(2018)通过对比发现ECMWF模式强降水预报量级偏弱、范围偏小，对暴雨和大暴雨漏报率高，但暴雨落区相比华东区域模式更精准；而华东区域模式则表现为预报量级偏强、范围偏大，对暴雨和大暴雨空报率高。因此，如何将不同模式预报进行有效融合，成为台站预报员在实际工作中急需解决的问题。

大量研究表明，多模式集成预报技术可以有效发挥不同模式各自的性能优势，同时减少各模式的系统性误差(杜钧和陈静，2010)，明显提高对强降水的预报水平(曹晓钟，2008；Krishnamurti et al., 2009；农孟松等，2011；康红文等，2012；狄靖月等，2013；李洁等，2014；唐圣钧等，2015；黄威和牛若芸，2017；刘汉武等，2017；钟伟等，2018；Wang et al., 2021)。多模式降水预报集成的关键是确定不同模式参与集成的系数。在台站降水预报业务中，预报员常通过对比历史相似降水过程中不同模式的降水预报效果来确定其可信程度，即确定不同模式参与集成的系数。近年来，气象学者们多从降水形势场相似出发，尝试了多钟筛选历史相似过程的客观方法。闫丽凤等(1999)采用车贝雪夫混合多项式对暴雨发生前期的高度场展开，并借此找到历史相似暴雨过程，进行最佳相似预报。陈静(2000)通过设计环流演变动态相似预报方法，从气压、温度、高度场出发对历史个例库进行滚动相似映射，效果较好。万日金等(2006)和付世军等(2018)均发现利用动力相似法筛选出的历史相似暴雨个例对当前降水落区、量级预报有较高的参考意义。但上述方法避开了大气内部的复杂物理过程以及复杂地形的动、热力影响，导致两个降水过程即便天气形势相似，其造成的降水特征也可能存在差异。随着当前基于机器学习的图像识别技术不断发展，李骞等(2011)提出了一种基于室外图像的天气现象识别方法，实现了对天气现象的自动观测。温家洪等(2019)利用图像识别技术实现了对历史近似暴雨洪涝灾害的快速检索。王山海等(2019)和洪思弟等(2020)分别利用卷积神经网络成功挖掘出卫星云图、雷达回波图和降水图像中的重要信息。

考虑到天气系统分类的多样性及其高低层作用的复杂性，另外模式降水预报场是天气系统相互作用的综合结果，降水场的强度和空间分布一定程度反映了当天的天气形势。本文尝试以降水预报场为基础，利用图像相似识别技术来进行相似历史个例检索，进而建立不同模式降水预报的客观集成方法。

1 资料和方法 1.1 资料说明

采用的实况数据为2016年5月—2019年12月华东区域范围内(109°—123°E，25°—38°N)所有国家站逐日(08—08时) 24 h累计降水量观测数据。采用的模式数据包括2016年5月—2019年12月华东区域气象中心提供的华东区域模式(WARMS 2.0)和ECMWF全球模式输出的逐日12—36 h的24 h累计降水预报数据，即两个模式起报时间均为20时(北京时，下同)。模式数据统一插值到(109°—123°E，25°—38°N)的范围，分辨率为0.05°。尽管ECMWF全球和华东区域模式自投入业务使用以来逐年均有改动升级，但近年来较大的更新分别出现在2016年春季和2014年(Malardel et al., 2016；徐同等，2016)，所以基于模式稳定性的考虑，本文并未采用2016年5月前的数据。

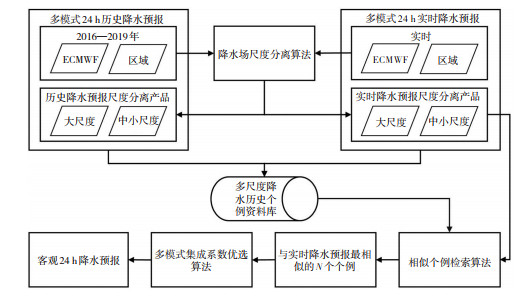
1.2 最优集成方法

采用的基于降水空间分布相似的最优集成技术主要是通过检索历史上与实时降水预报分布形态、强度相似的个例，寻找历史相似个例中不同模式降水预报的最优集成系数，并应用于当前时次的降水预报中。技术流程如图 1所示，主要包括以下三个步骤：

第一步，对实时与历史多模式24 h降水预报场进行尺度分离，建立持续更新的多尺度降水历史个例资料库。首先计算ECMWF全球和华东区域模式24 h累计降水预报的平均场。由于ECMWF全球模式对大范围大尺度的降水预报效果较好，对局地中小尺度对流降水预报效果偏差，华东区域模式则刚好相反(肖红茹等，2013；刘静等，2014；辛辰和漆梁波，2018；王万筠等，2018；党英娜，2018)，而两家模式的平均结果则兼有大尺度和中小尺度的降水特征。然后采用高斯低通滤波器(陈万海和赵春晖，2007)进行降水尺度分离。该低通滤波函数在频域上的形式为

$ H(x, y) = {e^{ - {D^2}(x, y)/2{\delta ^2}}} $

(1)

$ D(x, y) = \sqrt {{x^2} + {y^2}} $

(2)

D(x, y) 为频率域的原点到(x, y) 点的距离，δ用来衡量高斯曲线的广度。用截止频率D₀代替δ，则高斯低通滤波函数表示为

$ H(x, y) = {e^{ - {D^2}(x, y)/2D_0^2}} $

(3)

其中D₀值决定了分离的尺度大小。经过多次试验，采用D=2作为分界线将实时和历史上所有降水平均场分离成大尺度和中小尺度降水两部分，其中大尺度部分代表连续性成片降水，中小尺度部分代表局地分散性降水。分别将两种尺度的降水场绘制成图形文件，组建多尺度降水历史个例库。通过计算由多尺度降水场还原得到的集成平均降水场与原始集成平均降水场间的均方根误差，对比了理想低通滤波(杨柱中等，2014)、巴特沃斯低通滤波(李钟慎，2003)和高斯低通滤波器对原始降水场的还原效果。根据表 1中2017—2019年6—8月逐日(08—08时)多模式集成平均降水预报的尺度分离结果，由高斯低通滤波器分离出的多尺度降水场还原得到的集成平均降水场与原始集成平均降水场间的日平均均方根误差小于理想和巴特沃斯低通滤波器的结果，说明高斯低通滤波器在进行尺度分离的同时，对保持了原始降水场较高程度的还原，故选择高斯低通滤波作为尺度分离方案。

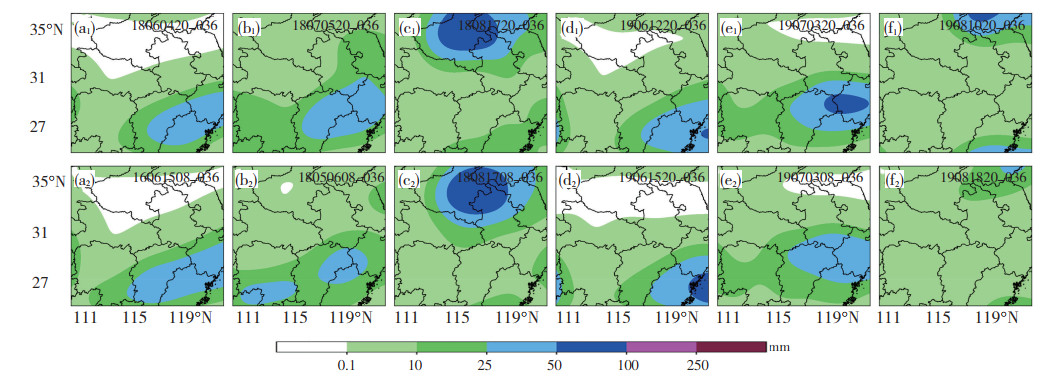
第二步，针对尺度分离后的实时降水预报，在历史个例资料库中检索与实时多模式24 h降水预报形态分布和强度相似的N个个例。检索时间段为选取所在月份的前后2个月，共计5个月，比如针对2019年6月1日的预报结果，检索时间段包括2017和2018年的4—8月和2019年的4—5月。定义相似指数为强度相似度和形态相似度的和，其中强度相似度采用尺度分离后的大尺度降水场的均方根误差来表示；形态相似采用图像哈希技术(季秀云，2014)进行检索，形态相似度以综合大尺度和中小尺度降水场与历史个例之间的汉明距离(季秀云，2014)来表示，汉明距离越小，表示两张图形越相似。根据相似指数从小到大的排列顺序，选取前15个历史个例参与下一阶段的运算，同时为避免出现选出的历史个例中存在相似程度有明显差距的情况，设定当任意两个连续排列个例的相似指数的差值≥5时，位于其后的历史个例将被剔除，所以不同时次的检索出的历史相似个例数N也不同(1≤N≤15)。图 2给出2018和2019年汛期共计6个时次降水预报所检索到的最相似历史个例，从中可见当前降水预报和历史相似个例的中雨以上量级雨带的分布整体较为相似，且二者强降水中心强度的偏差不超过一个量级。由此可见，结合均方根误差和图像哈希技术用来识别相似历史降水预报个例是可行的。

第三步，确定最优集成系数。针对选出的N个相似历史个例，首先通过系数遍历方式，为同期ECMWF和华东模式降水预报分别乘以一独立系数，系数取值范围均为0.1~2.0，间隔0.1，共计400种组合，形成400个融合降水预报场；其次利用降水观测资料，动态选出降水TS (Threat Score)评分最高的组合系数；为了避免只追求TS评分最高而导致降水空报过多的情况，只选取预报偏差Bias评分(计算公式见1.3节)位于[0.8，1.2]区间内的系数组合；最后将最优系统应用到实时的降水预报中，获得实时的降水集成预报。在系数组合优选过程中，首选标准为暴雨TS评分，如果预报场和实况场均无暴雨出现，则依次选择大雨、中雨、小雨TS评分。最后基于选出的N个相似历史个例，通过遍历方式选择晴雨分界线。分界线取值范围为0.1~5.0，间隔0.1，共计50个降水预报场。结合实况观测数据选出晴雨预报准确率最高时所对应的分界线应用到当前预报中。在计算降水TS、Bias评分和晴雨预报准确率P时，通过将降水预报结果插值到国家站点进行统一评分。

1.3 降水检验评估方法

降水预报场首先采用双线性插值到华东区域内(109°—123°E，25°—38°N)所有的国家站点再进行检验评估。检验评估方法为主要业务上常用两分类检验方法中的晴雨预报准确率P、TS评分(Ts)、Bias评分(Bias)，具体计算公式如下

$ P = \frac{{{N_{\rm{A}}} + {N_{\rm{D}}}}}{{{N_{\rm{A}}} + {N_{\rm{B}}} + {N_{\rm{C}}} + {N_{\rm{D}}}}} \times 100\% $

(4)

$ {T_{\rm{S}}} = \frac{{{N_{\rm{A}}}}}{{{N_{\rm{A}}} + {N_{\rm{B}}} + {N_{\rm{C}}}}} $

(5)

$ {B_{{\rm{ias}}}} = \frac{{{N_{\rm{A}}} + {N_{\rm{B}}}}}{{{N_{\rm{A}}} + {N_{\rm{C}}}}} $

(6)

上述公式中N_A、N_B、N_C、N_D分别为预报正确站数、空报站数、漏报站数和无降水预报正确站数。

考虑到同一地区逐年极端降水事件发生频次存在差异，仅用TS评分来评估模式暴雨预报略显不足。故本文在检验暴雨预报时补充采用了由Ferro和Stephenson (2011)提出的极端依赖指数(EDI)，该方法虽然可能会高估模式的实际预报能力，但由于其不依赖于暴雨的历史发生频率，所以能在一定程度上评估模式对不同时期极端降水的预报能力。EDI (I_ED)的计算公式如下

$ {I_{{\rm{ED}}}} = \frac{{\log F - \log H}}{{\log F + \log H}} $

(7)

其中F为空报率，F=N_B/(N_B +N_D)；H为击中率，H=N_A/(N_A+N_C)。I_ED取值范围为[-1，1]。

此外为了检验雨带位置的预报偏差，还引入了CRA空间检验技术。CRA方法是由Ebert等(Ebert and Mcbride, 2000；Ebert and Gallus, 2009)提出的一种基于目标(即单个雨带)的定量降水检验方法。CRA方法首先需要定义连续雨区或雨带的降水阈值。本文采用的降水阈值为25 mm·d^-1，然后在华东区域范围内对连续雨区进行识别。接着为了进一步分析预报产品的降水预报偏差来源，对连续雨区内强降水预报朝东南西北和东北、东南、西北、西南共八个方向进行平移，当平移后的强降水预报与实况间偏差平方和的平均数最小时，此平移距离即为预报产品与实况落区的偏差距离。具体计算公式详见符娇兰和代刊(2016)的研究。

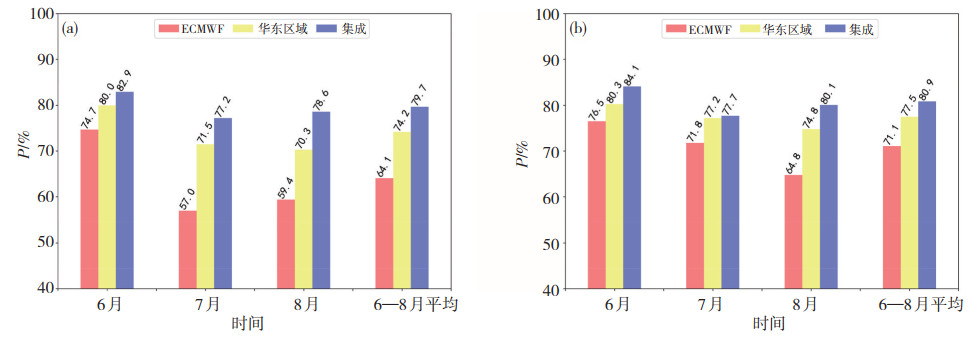
2 结果检验 2.1 总体检验评估

针对2018和2019年6—8月ECMWF全球模式、华东区域模式和多模式最优集成产品的24 h降水预报进行了检验评估。为了模拟实时预报流程，此处计算多模式最优集成预报时所用的历史降水个例资料库均是由该预报时刻之前的多模式数据构建的，从而避免影响集成产品检验的独立性；同时集成算法运行过程中，新的预报数据会持续对历史个例库进行动态更新补充。图 3a给出了2018年6—8月多模式24 h降水预报晴雨准确率的分布情况。从整体汛期(6—8月)来看，最优集成产品的晴雨准确率接近80%，明显高于ECMWF全球和华东区域模式的结果。从逐月分布情况来看，各家模式均在6月份表现较好，准确率均在70%以上；而7—8月ECMWF全球和华东区域模式的准确率相比6月出现了明显下降，下降幅度接近15个百分点。这主要是由于6月副热带高压脊线位于20°—26°N附近，华东地区普遍进入主汛期，降水过程多以切变线、江淮气旋、梅雨锋等引起的系统性降水为主，模式预报较为稳定；进入7月后，台风登陆引发的暴雨以及飑线、超级单体等对流系统引发的短时强降水过程增多(于波等，2013；吴瑞姣等，2019)，而模式对以上降水过程的预报能力有所欠缺所导致的。相比之下最优集成产品的准确率虽也有下降，但幅度相对较小。2019年的检验结果与2018年较为相似(图 3b)，即晴雨准确率方面，多模式最优集成产品相比单模式有着较为明显的提高，且其预报准确率随时间变化幅度较小，更加稳定。

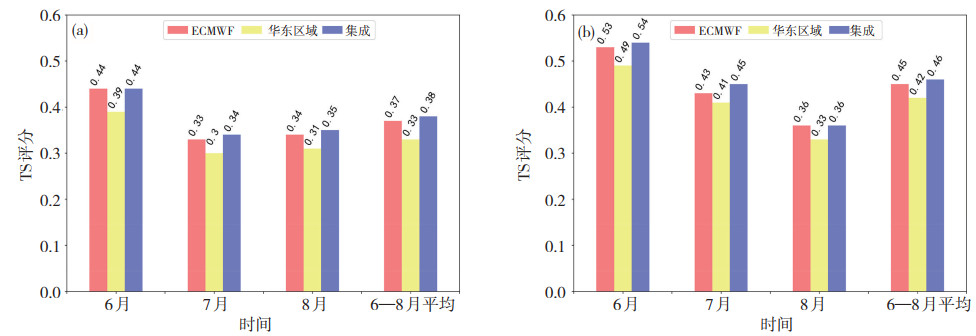
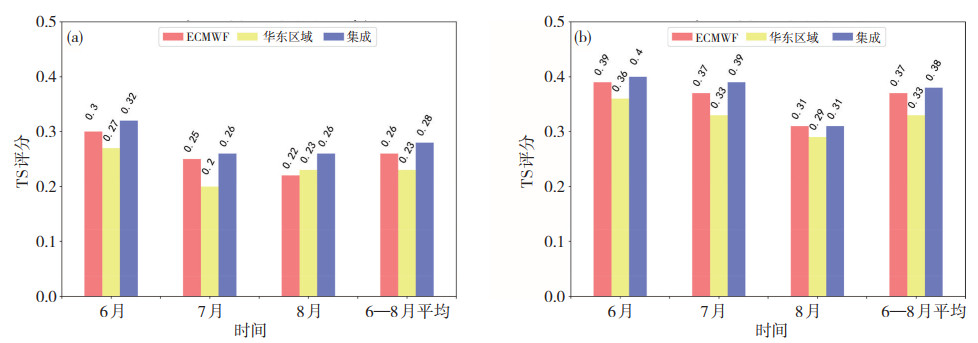
图 4为各家产品24 h中雨以上量级降水的TS评分结果，可以看出ECMWF模式和集成产品对2018和2019年汛期中雨以上量级降水的预报评分相差很小，而华东区域模式评分相对偏低。对比24 h大雨以上量级降水的TS评分结果，发现也存在相似的现象(图 5)。分别统计集成产品中ECMWF和华东区域模式各自的权重系数，发现2018年ECMWF模式平均权重系数为0.9，华东区域模式为0.3；2019年ECMWF模式为0.8，华东区域模式为0.4，即集成产品中ECMWF模式预报所占比重较大(表 2)，且根据对中雨及大雨以上量级的检验结果来看，ECMWF模式均明显好于华东区域模式，这就导致了集成产品的检验结果也会更接近ECMWF模式。同时由于集成产品中还加入了一部分华东区域模式预报，导致其中雨及大雨预报范围相比单模式偏大，进而使得其中雨及大雨TS评分相比单模式出现小幅增长。另外，从逐月评分来看2018— 2019年各家产品在对中雨和大雨以上量级降水预报方面均表现为6月好于7、8月，这依然可能与6月份华东地区系统性降水偏多，而7—8月受台风和强对流天气影响较明显有关。综上，从对中雨和大雨以上量级降水的预报效果来看，多模式最优集成产品相比单模式有一定程度的提升，整体更接近ECMWF模式的预报结果。

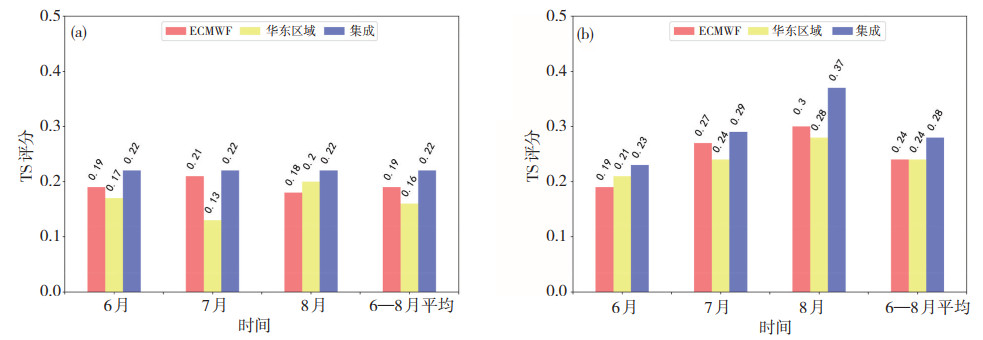
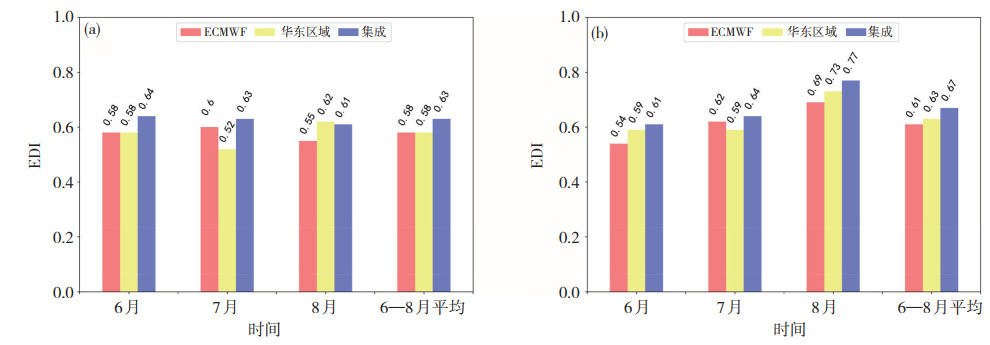
图 6给出2018—2019年6—8月各模式24 h暴雨TS评分结果。从整体汛期来看，2018年各家模式的暴雨评分普遍在0.2左右，而2019年则提升至0.25左右，多模式集成产品整体表现好于单模式。从逐月评分来看，当ECMWF和华东区域模式的暴雨评分均较为接近，此时集成产品的暴雨评分相较于单模式而言有明显提升，特别是2019年8月份提升幅度达到0.07；而当单模式间预报评分差距较大时，如2018年7月ECMWF模式的暴雨评分超过0.2，但华东区域模式则比ECMWF低了0.08，集成产品的暴雨评分相较于单模式而言并未出现明显改善。图 7为24 h暴雨极端依赖指数EDI的检验结果，可以看出无论是从逐月还是整体汛期来看，集成产品对暴雨的预报能力均好于单模式，但依旧存在单模式间预报效果相差较大时集成产品改进效果不明显的现象。究其原因，可能是因为多模式集成产品是由ECMWF和华东区域两家模式预报按不同权重相加得到的，所以当单模式间暴雨评分相差较大时，集成产品必然会受到评分较低的那个模式预报的影响。此外，与TS评分结果相似，2019年各家模式的暴雨预报EDI相比2018年也有所提高，考虑到EDI不受暴雨历史发生频率的影响，由此可以说明ECMWF和华东区域模式预报对2019年的极端降水预报水平相比2018年有所提高。

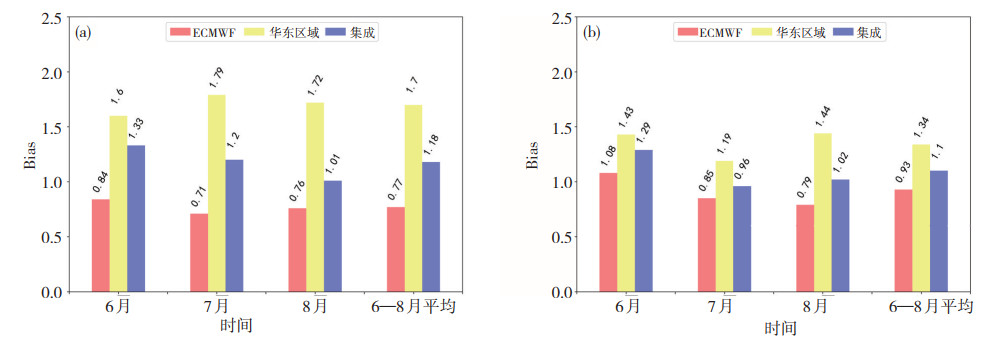
计算2018和2019年6—8月各模式24 h暴雨Bias偏大，存在不少空报、漏报情况；ECMWF模式的偏差偏差，可以看出华东区域模式的偏差值整体偏高，但值最小，暴雨TS评分排名中间，说明ECMWF模式预其暴雨TS评分偏低，说明华东区域模式预报暴雨范围报暴雨范围偏小，但预报准确率相比华东区域模式较高；集成产品的偏差值则处于ECMWF和华东区域模式之间，整体更接近1，同时其暴雨TS评分最高，说明集成产品可以在增大暴雨点命中率的同时，一定程度上减少空报漏报的出现(图 8)。

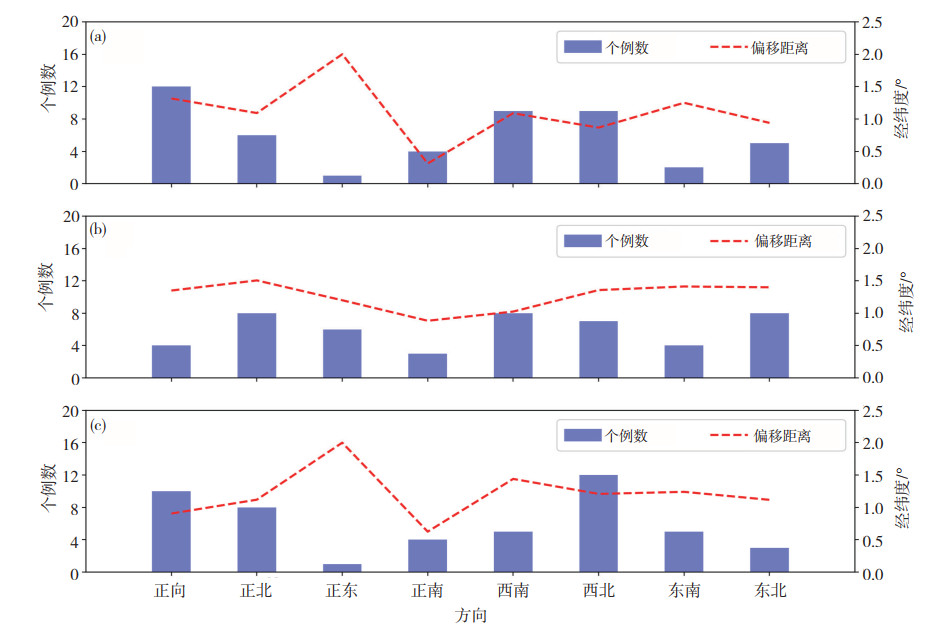
为了对比各家预报产品对强降水落区的预报情况，引入CRA空间检验技术对预报强降水落区相比实况的偏移程度进行分析。基于24 h累计降水量超过25 mm的连续雨区标准，从2018—2019年6—8月共识别出降水个例共计48个。图 9给出了各家预报产品的强降水落区相比实况在各个方向上偏移的个例数及平均偏移距离，结果显示ECMWF模式和集成产品的强降水落区均整体偏西，集中在实况落区的正西、西北和西南方向，偏西占比分别达到总数的62.5%和56.3%，平均偏移距离分别为1.11和1.13个经纬度(图 9a、c)；而华东区域模式在各个偏移方向上的分布则相对较为平均，主要集中在正北、东北、西北和西南方向，预报落区整体偏北，占个例总数的48%，平均偏移距离1.42个经纬度(图 9b)。可以看出，ECMWF模式的强降水落区位置与实况的偏差距离最小，预报效果最好，而相比之下华东区域模式对强降水落区的预报能力则相对偏弱。集成产品无论是对强降水落区的预报能力还是落区整体偏移方向均与ECMWF模式相接近。

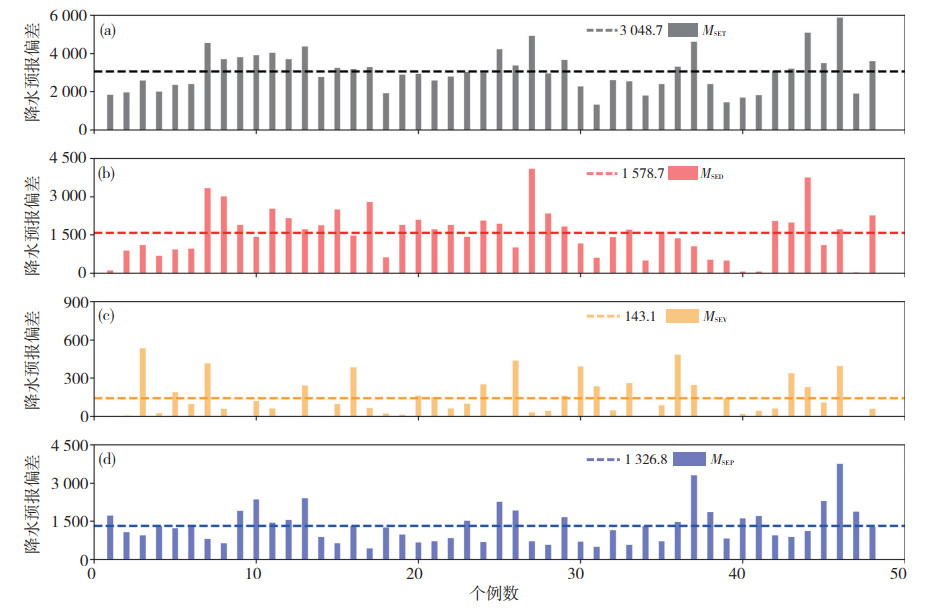
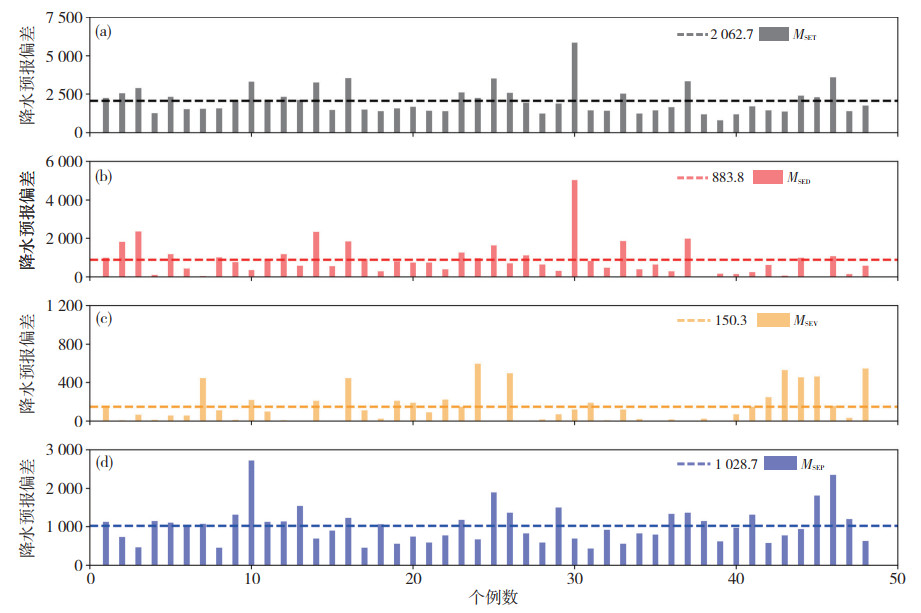
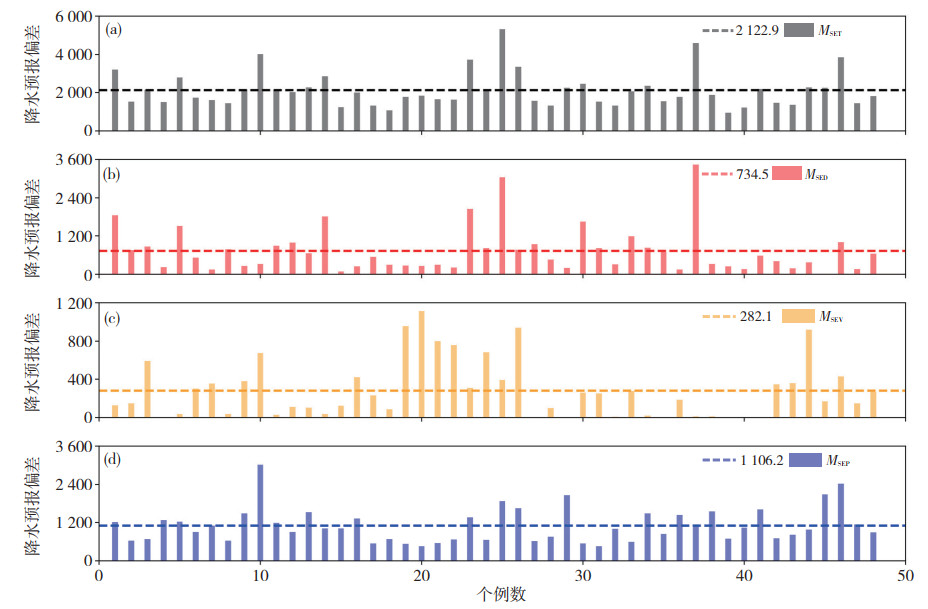
图 10—12给出了各家预报产品的降水偏差分析。从整体偏差来看，集成产品对大雨以上量级降水的预报偏差最小，效果最好；ECMWF模式次之，华东区域模式则偏差较大。进一步分析可知，ECMWF模式的落区偏差(M_SED)无论是从确定值还是占比来看，均明显小于华东区域模式，但在强度偏差(M_SEV)方面ECMWF模式的确定值和占比几乎是华东区域模式的两倍，且其形态偏差(M_SEP)占比超过了50% (表 3)。根据符娇兰和代刊(2016)对西南地区强降水过程的CRA分析来看，降水的形态特征主要与中尺度对流系统活动有关，而全球模式在刻画中尺度对流活动方面明显存在不足。总体来看，ECMWF模式对大雨以上量级的降水落区位置预报较好，但强度预报偏弱；华东区域模式则与ECMWF模式刚好相反，这也与前人的研究结论基本一致(党英娜，2018)。而从集成产品的结果来看，虽然其落区误差相比ECMWF模式略有增长，但整体效果依旧明显好于华东区域模式；而其在强度误差方面则明显优于ECMWF模式。上述结果说明集成产品既在一定程度上弥补了全球模式在预报中尺度降水过程时强度偏弱的劣势，又纠正了区域模式在降水落区预报方面的偏差。

2.2 典型个例检验评估结果

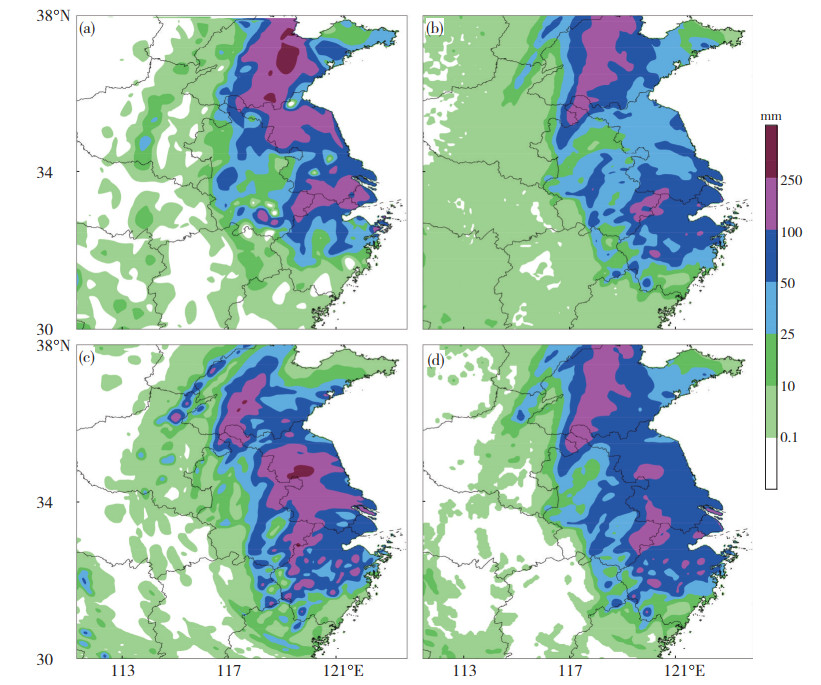
挑选了2019年的一次暴雨个例来进一步对比集成产品和单模式的优劣性。2019年8月10日08—11日08时，台风“利奇马”登陆后北上引发我国沿海东部部分地区出现暴雨甚至大暴雨天气，特别是山东中部局地出现了250 mm以上的特大暴雨(图 13a)。利用CRA方法进行强降水落区检验，发现本次暴雨过程各家预报产品的强降水落区相比实况均出现不同程度偏西情况，其中ECMWF模式整体偏西了0.85个经纬度(表 4)，且对江苏中北部地区的降水强度预报偏弱，暴雨存在明显的漏报情况，但对山东中部的暴雨预报效果较好(图 13b)；华东区域模式整体偏西南方向约1.0个经纬度，尤其是对山东境内暴雨区的预报偏移情况最明显，范围也偏小，但是对江苏境内的暴雨落区预报较为准确(图 13c)；而多模式集成产品则很好地中和了以上两家模式的优点，既弥补了ECMWF模式对江苏境内暴雨的漏报情况，又将华东区域模式在山东中部的暴雨区向东移动、扩展(图 13d)，对应其暴雨TS评分也较单模式有明显提高。

对比表 4中各家预报产品的强降水落区与实况的偏差情况，发现集成产品的总体偏差(M_SET)最小，ECMWF模式次之，华东区域模式最大。进一步分析偏差来源，可以看出各家产品的偏差主要来源于形态偏差(M_SEP)，这主要与台风利奇马外围螺旋雨带中中小尺度对流活动旺盛有关；在位移偏差(M_SED)方面，集成产品与ECMWF模式且均远小于华东区域模式，落区预报相对准确；在强度偏差(M_SEV)方面，不同于ECMWF和华东区域模式分别由于部分地区出现强降水漏报而导致偏差较大的情况，集成产品反而因综合了两家模式强降水落区，从而减少了单模式在不同区域出现强降水漏报的情况，强度偏差(M_SEV)也随之降低。综上，基于降水空间分布相似的多模式集成技术在预报该个例的强降水落区位置和强度方面相比单模式更具优势。

3 结论

利用ECMWF全球模式和华东区域模式的24 h累计降水预报数据，建立华东区域历史降水个例资料库，通过寻找历史上与实时降水预报分布形态、强度相似的个例，判断该个例中不同模式的降水预报效果，并以此为基础调整当前各模式在集成预报中的比重，从而实现对实时多模式降水预报的最优集成。对比集成产品和ECMWF、华东区域模式针对2018—2019年6—8月汛期降水过程的检验结果，得出主要结论如下：

(1) 多模式集成产品的晴雨预报准确率相较于单模式而言有着明显提高，且不同于单模式晴雨准确率随时间变化幅度较大，集成产品则表现相对稳定，晴雨准确率始终维持在75%以上。从分量级降水检验结果来看，集成产品对各量级降水预报的整体表现均好于单模式，且当单模式间预报评分相近时，集成产品相比单模式的预报效果提升得更加明显。同时，集成产品的暴雨Bias偏差基本处于华东和ECMWF模式之间，偏差值接近1，说明相较于ECMWF模式暴雨范围偏小、华东偏大的特点，集成产品可以在两者中取得一定的平衡，在保证暴雨点命中率的同时，有效减少空漏报情况。

(2) 利用CRA空间检验技术对从2018—2019年6—8月的48个强降水个例进行检验，结果显示ECMWF模式和集成产品的强降水落区相比实况整体偏西，华东区域模则相对偏北。分析降水偏差构成，ECMWF模式的位移偏差明显小于华东区域模式，但其强度偏差偏大，说明ECMWF模式对强降水落区位置预报较好，但强度预报偏弱；华东区域模式则刚好相反。集成产品既能在一定程度上弥补全球模式在预报中尺度降水过程时强度偏弱的劣势，又纠正了华东区域模式在降水落区预报方面的偏差。

(3) 对台风“利奇马”登陆北上引发暴雨的个例进行分析，发现集成产品能有效综合华东区域和ECMWF模式的强降水落区，在避免大幅度扩大强降水预报范围的条件下，减少了单模式在不同区域出现漏报的情况，使得其位移偏差和强度偏差出现明显下降，进而实现了暴雨TS评分的提高。

然而，基于降水空间分布相似的多模式集成产品依旧存在一些问题：由于集成产品是由ECMWF和华东区域模式预报按权重相加获得的，所以在两家模式预报出现明显分歧或者效果均不理想的情况下，该产品针对单模式预报效果的提升较为有限。另外，数值模式的升级调整可能也会对集成结果造成影响。后期考虑通过增加参与集成的模式预报产品、引入天气形势背景相似等方式对算法进行改进。