引言

旱涝是长江流域的主要气象灾害，近年来的观测事实和相关科学研究都表明长江流域极端降水事件发生的频率正在不断增加，范围不断扩大。1998年长江全流域性大洪水、2016年长江中游“暴力梅”、2017年长江中下游区域性大洪水、2020年超长梅雨，均引发了严重的洪涝及地质灾害。与此同时，极端少雨事件也频繁发生，2018年盛夏江汉大部降水偏少2~5成，出现伏旱；2019年长江中下游地区出现近40a来最严重的伏秋连旱。频繁发生的极端事件给社会经济发展带来越来越严重的影响，也因此受到越来越多的关注。目前针对极端事件的研究有很多，但诊断对象通常是单日或几日强降水过程，或是以月、季内日降水量极值、暴雨日数等作为极端降水指数(Karl and Knight, 1998；Zhai et al., 1999；Goswami et al., 2006；陈峪等，2010；任国玉等，2010)。针对长江流域的研究，也主要以日降水作为研究对象(杨宏青等，2005；张天宇等，2007；张文等，2007；杨玮和程智，2015；高洁，2019)。

气候上，单次或几次强降水过程并不足以概括更长时间尺度的特征，月、季尺度总降水量亦是很重要的研究内容，直接关系到是否会出现极端事件。另一方面，天气尺度的极端降水事件研究对象往往是极端多雨，但气候尺度上则更为关注月、季极端少雨及其影响。本研究着眼于长江流域月、季尺度的极端降水，探讨更长时间尺度的“极端降水气候事件”的判定方法。

“极端降水气候事件”是气候领域的概念，区别于通常所说的“日极端降水过程”，对于月、季平均的气候要素，采用极值的思想进行分析，能在更长时间尺度上描述气候的异常状况。气候概率统计学上，对气候要素极值的概率统计主要有两种方法，一种是基于统计样本的百分位法，该方法目前多用来对日极端降水进行挑选，如翟盘茂和潘晓华(2003)、张家国等(2018)以1961—1990年逐年日降水量的第99个百分位值的30 a均值定义极端降水事件的阈值，苏布达等(2006)考虑了长江上游降水的特殊性，利用95%分位降水量代替常规的暴雨标准50 mm定义了极端强降水事件，陈波等(2010)对华中地区四个不同百分位的强降水事件进行了区分，苏志重等(2016)、唐永兰等(2018)、郑小华(2019)采用95百分位法在年极端降水总量、频次、最大日降水量及强度等4种指数上对极端降水进行描述；另一种是用某种概率分布模型对气候要素值进行拟合，常用的分布型如皮尔逊一Ⅲ型曲线、耿贝尔分布、正态分布等，根据气候值的概率对极端事件进行分析(罗梦森等，2013；伍丽丽等，2013；曹洁等，2014；陈子燊等，2015；崔玫意等，2017)，或是对气候要素的重现期进行估算等(陈建昌等，1995；林两位和王莉萍，2005；梁忠民等，2016；何干皓等，2017；杜晓阳等，2018；牟婷婷，2018)。有研究表明，经正态分布转换后的数据具有明显统计优势(罗梦森等，2013)。而Box-Cox变换和正态分布有机结合构建的新的Box-Cox正态分布，在研究降水极值分布(崔玫意等，2017)和气温极值方面(曹洁等，2014)，拟合效果要优于常用的广义极值(GEV)等分布。本研究将这一方法引入气候极端事件领域，采用正态分布模型对降水进行拟合，再结合百分位法，判断“极端降水气候事件”，对常规百分位法进行一定改进。

1 资料与方法 1.1 资料及处理

资料为1961—2017年长江全流域700个气象站点逐月降水资料，来源于国家气象信息中心。

采用泰森多边形法(Thiessen, 1911)，将站点降水资料转化成流域面雨量资料。为了尽可能减少缺测站及迁站的影响，根据站点变化动态调整泰森多边形边界。

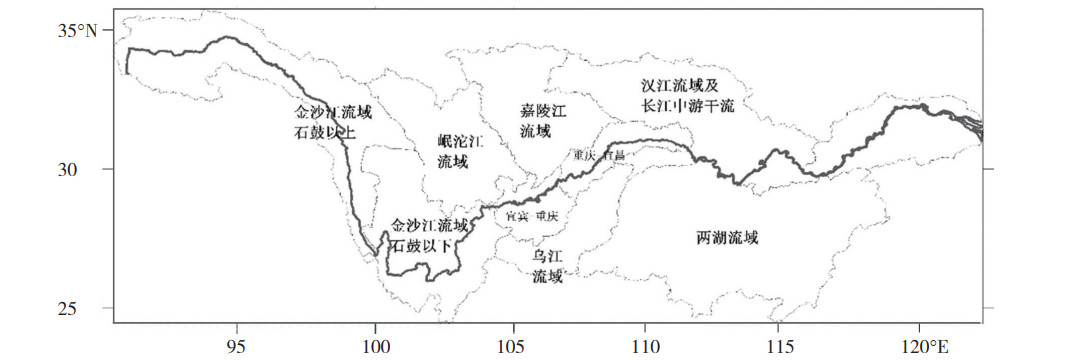
1.2 流域分区

依据自然地理条件及气候业务需求，将长江流域划分为9个子流域，分别是金沙江流域石鼓以上、金沙江流域石鼓以下、岷沱江流域、嘉陵江流域、乌江流域、宜宾-重庆区间、重庆-宜昌区间、汉江流域及长江中游干流区间、两湖流域(洞庭湖流域和鄱阳湖流域)，空间分区见图 1。

1.3 分布转换方法(Box-Cox变换)

各种气象要素的概率分布都存在不同程度的偏态特征(曹杰和陶云，2002；曹洁等，2014；郭凌曜和李英，2015)，研究表明(杜良敏等，2018)，长江流域月降水量经常呈Gamma分布，正态通过率低，而季节降水通过正态检验的站点比率相对月降水略高，但也仍是正态分布、Gamma分布各占一半。统计分析时需要对序列进行正态分布转换，常用的方法有Box-Cox变换、Yeo-Johnson变换等。

本文采用Box-Cox变换，将具有一定偏态分布的降水及面雨量序列转换为近似符合正态分布的新序列，以便利用已有的数理统计方法研究数据的统计规律和特征。Box-Cox变换是统计建模中的常用方法，该变换可以使线性回归模型在不丢失信息的同时，具有良好统计性质，由Box和Cox提出。

该变换的表达式为

$ Y_{i}(\lambda)=\left\{\begin{array}{l} \frac{y_{i}^{\lambda}-1}{\lambda}, \lambda \neq 0 \\ \ln y_{i}, \lambda=0 \end{array}\right. $

(1)

其中，λ是一个待定的变换参数，最佳λ值由python程序中scipy.stat.boxcox函数自动生成，为极大似然相似估计值。

逆变换表达式为

$ Y_{i}=\left\{\begin{array}{l} \left(\frac{1+\lambda y_{i}(\lambda)}{\lambda}\right)^{\frac{1}{\lambda}}, \lambda \neq 0 \\ \exp \left(y_{i}(\lambda)\right), \lambda=0 \end{array}\right. $

(2)

利用Box-Cox变换可将原始计算所得的面雨量序列转化为近似符合正态分布的新序列。

2 Box-Cox变换在长江流域极端降水气候事件判定中的应用 2.1 极端降水气候事件的判定

判定极端降水气候事件采用基于Box-Cox正态分布转换后的百分位法(以下简称“Box-Cox百分位法”)。

将一个原始面雨量序列经过Box-Cox变换后得到一个近似正态分布的新面雨量序列，计算出各年面雨量在正态分布中所占百分比，取10%和90%百分位反算出对应的原始面雨量值作为阈值。定义10%对应的面雨量值为极端少雨气候事件阈值、90%对应的面雨量值为极端多雨气候事件阈值。变换后的面雨量小于少雨阈值的年份定义为发生极端少雨事件、面雨量大于多雨阈值的年份定义为发生极端多雨事件。

2.2 Box-Cox百分位法与常规百分位法对极端阈值拟合的比较

常规百分位法是直接在降水序列排序基础上，取相应百分位处的值作为阈值，但这种方法的前提实际上是假定了数据遵循正态分布，在这种正态假设不成立的情况下，所挑选的阈值随着时间序列的延长或者缩短，会产生很大变化。而采用Box-Cox百分位法挑选出来的阈值，由于原始数据经过了正态化处理，则有效解决了常规百分位法的上述问题。

以夏季为例，采用Box-Cox百分位法提取的阈值与常规百分位法的阈值列于表 1，可以看出，当参与排序的面雨量序列长度发生变化时，常规百分位法阈值在一部分流域发生明显变化，主要有岷沱江流域、重庆-宜昌区间、两湖流域等，阈值浮动超过30 mm(以“*”标出)；而Box-Cox百分位法阈值变化显著减小，绝大多数流域变动在10 mm之内。

另一方面，Box-Cox百分位法在短时序数据处理上更具优势。对比两种方法相同时间长度的阈值，相比于30 a，50 a长度下阈值变化明显减小。表明，当序列足够长时，是否经过Box-Cox转换，对阈值的影响不大；但当数据长度较短时，Box-Cox转换则显现出明显的稳健特性。

图 2a为原始面雨量序列通过正态检验情况，深色流域表示未通过正态分布检验，浅色流域为通过正态分布检验。经Box-Cox变换后，原始面雨量序列被转换成了更为近似正态分布的新面雨量序列，下文将其称为“Box-Cox面雨量序列”，由图 2b可见，全部子流域Box-Cox面雨量序列在月、季、年各时间尺度上均通过Lilliefors正态分布检验。

2.3 Box-Cox变换在长江流域极端降水气候事件判定中的应用初探

分别选择不满足正态分布的嘉陵江流域秋季(9— 11月)面雨量序列，和满足正态分布的岷沱江流域秋季(9—11月)面雨量序列进行应用对比。

嘉陵江流域秋季的原始面雨量序列不满足正态分布，面雨量在190~200 mm出现频次最多(图 3a)，相对于平均值235 mm具有明显偏移；出现这种偏态分布的原因在于面雨量的年代际分布不均，20世纪80年代中后期至2010年之间，面雨量均值维持在200 mm左右，与全序列均值相差较大(图 3c)；图 4为嘉陵江流域秋季极端降水气候事件的年代际频次分布，从中可见，在80年代中后期至2010年期间发生了4次极端少雨气候事件，分别在1991、1997、1998、2002年，4 a秋季面雨量均仅有140~160 mm。而与之对比，岷沱江流域1961年以来秋季面雨量呈缓慢减少趋势(图 5c)，很少出现明显的年代际雨量分布不均，因此该流域原始面雨量序列本身就满足正态分布(图 5a)。

对嘉陵江流域秋季面雨量采用Box-Cox正态分布转换后的序列频次分布如图 3b，拟合序列均值为2.5，与拟合频次分布最大值一致，满足正态分布。对比图 3c可以看出，Box-Cox面雨量序列与原始面雨量序列的逐年变化趋势一致，拟合序列仅在y轴方向进行了拉伸(或压缩)。而对于岷沱江流域，为了保证不同子流域间极端阈值挑选规则的一致性，对这类满足正态分布的序列，我们依然对其进行Box-Cox正态转换，转换后的序列将比其原始序列更接近标准正态分布型(图 5b)。岷沱江秋季原始面雨量序列极端多雨、少雨阈值分别为237.4 mm和152.7 mm，转换后则为240 mm和154.9 mm，仅有微小变化，不影响极端年份的选取。

2.4 2018年汛期(6—8月)长江各子流域极端降水气候事件判定应用

2018年汛期，长江上游降水实况分布为西多东少，上游西北部的岷沱江流域和嘉陵江流域北部降水偏多1~5成，上游其他子流域偏少1~5成。

采用Box-Cox百分位法计算1961—2017年汛期长江各子流域极端降水气候事件阈值(表 2)。利用阈值对2018年汛期面雨量实况进行判定，则岷沱江流域面雨量超过极端多雨气候事件阈值，判定为发生极端多雨气候事件，面雨量偏多排历史第4位；而长江干流重庆-宜昌段、汉江及中游干流区间面雨量超过极端少雨气候事件阈值，判定为发生极端少雨气候事件，面雨量偏少均排在历史第7位。而按照常规百分位法，1961—2018年共58 a，仅能筛选出极端多雨、少雨气候事件各6 a (约占10%)，那么干流重庆-宜昌段、汉江及中游干流两个子流域则未达到极端少雨气候事件标准。

同样按常规百分位法，若将新增年份并入序列，计算1961—2018年汛期岷沱江流域极端降水气候事件阈值，极端年份发生改变，极端多雨阈值由原来的532.7 mm (1988年)调整为545.0 mm (1981年)，原来排第6位的1988年不再是夏季极端多雨年。但采用Box-Cox百分位法得到的极端阈值仅发生微小变化，由542.5 mm上升为548.2 mm，无论是阈值还是极端年份的改变均不如常规百分位法剧烈，具有更为稳健的特性。

3 结论与讨论

本文在长江流域分区面雨量研究中引入Box-Cox正态分布转换方法，对长江流域面雨量进行正态分布拟合，并展开了流域极端降水气候事件阈值的研究，得到以下结论。

(1) 经Box-Cox变换，部分因降水年代际分布不均导致面雨量呈偏态分布特征的子流域，其拟合序列能转换为正态分布序列，而其他原始序列符合正态分布特征的流域，经转换后则更为接近标准正态分布型。

(2) 相较于常规百分位法，Box-Cox百分位法能一定程度上降低因为延长序列带来的阈值波动。经转换后得到的阈值，受序列长度变化的影响明显减小，具有更为稳健的特性。

(3) 当序列足够长时，经过Box-Cox转换与否，对阈值的影响不大；但在短时序数据处理上，Box-Cox百分位法比常规百分位法稳定，更具优势。

(4) 根据1961—2017年极端降水气候事件的阈值，判定2018年汛期(6—8月)，岷沱江流域发生了极端多雨气候事件，长江干流重庆-宜昌段、汉江及中游干流区间发生了极端少雨气候事件。

长江流域地形复杂，地理跨度大，降水变化原因复杂，不同子流域间地形差异对极端事件阈值的影响方面还有待深入研究。而阈值判定也只是极端降水气候事件研究的开始，依据此阈值挑选出来的极端降水气候事件，具有何种特征、形成机理等方面有待进一步的研究和诊断。