引言

长江流域横跨中国东部、中部和西部三大经济区，河流湖库众多，暴雨洪涝灾害频发。为趋利避害，流域内先后兴建了数万座大小水库，特别是三峡-葛洲坝、金沙江下游梯级水库在减灾兴利中具骨干作用。增强定量降水预报水平、提高洪水预报精度，优化上游水库群对中下游防洪补偿调度的库容分配、水位控制，已成为长江水旱灾害防御的重点。0~3 h短临预报作为定量降水预报的重要一环，目前的解决方案主要是监测外推或数值预报。直接使用数值模式输出结果(崔讲学等，2018)依然是流域水文气象预报业务的主要方法，然而因数值预报模式起转问题，初始几小时的预报结果常较大偏离于实况。由于雷达回波外推在前3 h内的预报效果要好于数值模式预报(王丹等，2014)，气象部门0~3 h短临预报的业务一般采取基于雷达数据的定量降水估算及监测外推(金荣花等，2019)。因此，将短临预报技术的最新进展应用于长江流域定量降水预报，对有效提高洪水预报精度具有重要意义。

气象部门短临预报业务主要是基于雷达数据的雷暴识别追踪和外推，包括单体质心法和交叉相关法。以TITAN (Thunderstorm Identification Tracking Analy- sis and Nowcasting)(侯正俊等，2018)和SCIT (Storm Cell Identification and Tracking)(王芬等，2010)为代表的单体质心法主要应用于对流降水系统。TREC (交叉相关法)通过风场外推，既可以跟踪对流降水系统, 也可以跟踪层状云降水系统，在短临预报业务中得到了广泛应用(张亚萍等，2010)，但由于其对变化较快的强对流降水系统风场外推质量迅速下降常出现跟踪失败。

为改进矢量风场的计算效果，针对交叉相关法存在的不足，近年来计算机视觉领域中的光流法( Gib-son，1950；Horn and Schunck, 1981；Lucas and Kanade，1981；Baker et al., 2009)被引入气象领域，尝试使用光流法计算的雷达回波矢量场来代替TREC风场，取得了较好的进展：如利用基于全局平滑的HS(Horn-Sc- hunck)光流场计算方法(韩雷等，2008)，改进了北京单部雷达的外推预报效果；利用局部平滑约束的LK (Lu- cas-Kanade)光流场计算方法(曹春燕等，2015)，改善了广东省10部雷达的回波拼图外推结果；而王志斌等(2017)尝试克服HS法易出现局部最小化和LK整场不易满足最优条件的不足，提出了综合HS法、LK法的改进光流法，发现对湖北省6部雷达的回波拼图外推结果较单独使用一种方法有较好的改进，之后又提出了用变分光流法作进一步改进(王志斌等，2019)。本文即以王志斌等(2019)提出的变分光流法为基础，结合新近发展的融合网格实况，对2020年整个长江流域的降水短临外推预报效果进行检验评估，探讨短临预报业务发展成果应用于流域服务业务的可行性，尝试为长江洪水防御和资源化利用提供更加精准的气象支撑。

1 资料与方法 1.1 资料

(1) 水文站资料：使用长江流域主要控制站三峡、莲花塘、汉口、大通等站的日最高水位、日最大流量。2020年为20世纪以来，继1931年、1954年、1998年后，长江再次出现的罕见流域性大洪水。汛期长江上游发生了5次编号洪水，三峡最大入库流量见表 1。

中游汉口站7月6日—8月7日连续33 d超警戒水位，最大流量7月29日61 400 m³·s^-1，莲花塘站7月5日—9月1日连续59 d超警戒水位，其中6 d超保证水位；下游大通站7月6日—8月10日连续36 d超警戒水位，最大流量7月13日84 600 m³·s^-1。

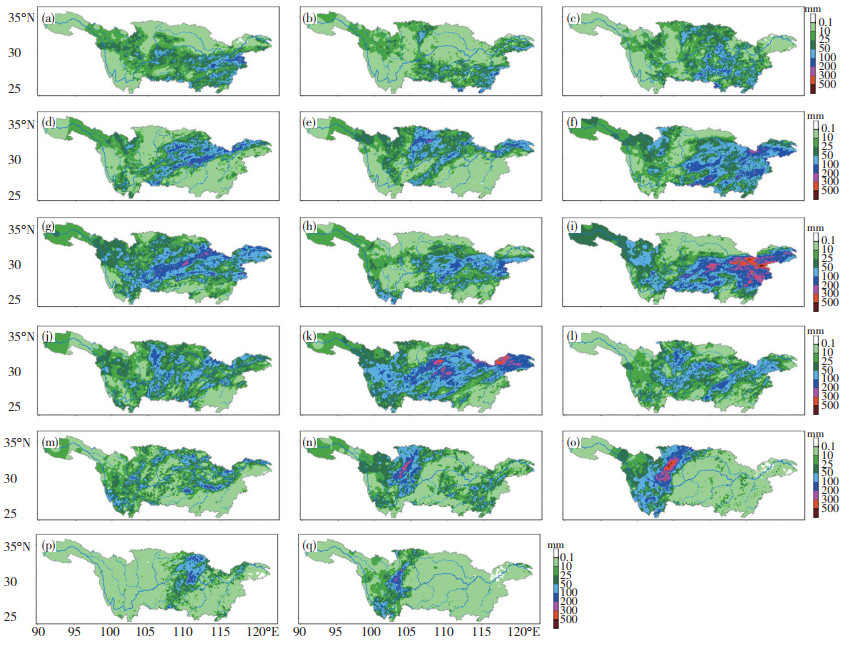
(2) 气象站资料：包括2020年长江流域736个国家自动气象站和20 360个区域自动气象站逐小时降水资料。本文主要针对国家质控考核质量较好的国家气象站降水作检验评估，地方性加密服务的区域气象站用于降水空间分布与量级的定性分析。引发2020年长江流域性大洪水的共有17次降水过程，其中6月7次，分别为1—3日、5—7日、7—9日、11—13日、15— 17日、20—25日、26—30日；7月5次，分别为1—3日、4—9日、10—12日、14—19日、24—27日；8月5次，分别为6—9日、10—12日、14—17日、19—20日、29—30日。历次降水过程降雨分布见图 1。

(3) 格点实况资料：应用于降水评估的格点实况使用中国气象局国家气象信息中心的2020年全国智能网格实况地面—卫星—雷达三源融合降水分析逐小时产品(潘旸等，2015)，空间分辨率5 km×5 km，其结合了地面气象站、卫星、雷达不同来源降水资料的优势(李红莉等，2009)。该产品对长江流域降水的估算结果平均较实况数值偏小(许冠宇等，2020)，降水量级越大，估算误差越大，不分量级其平均绝对误差率在20%~30%。

(4) 雷达资料：长江流域四川、贵州、云南、重庆、陕西、湖北、湖南、江西、安徽、上海、浙江等省市共84部多普勒雷达逐6 min观测资料，对每部雷达采取模糊逻辑法进行质量控制(吴涛等，2013)，三维拼图使用极坐标向三维直角坐标的转换(肖艳姣等，2006)，单站雷达之间重叠部分采用高斯距离加权方法进行插值，并利用5点平滑对全场进行平滑处理。

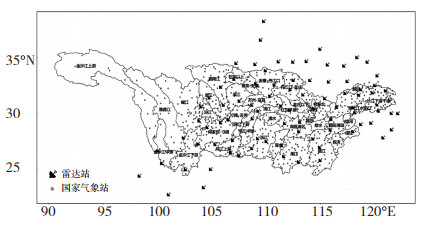
为了评估降水临近预报在各个子流域的效果，本文将长江流域划分为39个子流域进行分区检验，包括金沙江上游、金沙江中游、金沙江下游、雅砻江、岷江、沱江、向家坝-寸滩、涪江、嘉陵江、渠江、寸滩-万州、万州-宜昌、乌江上游、乌江中游、乌江下游、石泉以上、石泉-安康、安康-丹江口、丹江口-皇庄、皇庄以下、江汉平原、武汉、鄂东北、陆水、清江、澧水、沅江、洞庭湖区、资水、湘江、修水、赣江、鄱阳湖区、饶河、信江、抚河、青弋江水阳江、滁河、长江下游干流。其中金沙江上中游、雅砻江以及岷江、嘉陵江两江西部的雷达和自动站明显覆盖不足，不仅相关区域的雷达外推预报效果难以保证，而且格式实况降水误差也很大，原因是格式实况降水主要靠卫星估测，但卫星主要反映的是天气系统顶部信息，因此上述子流域分区的预报效果参考性不强。39个子流域、84部雷达、736个国家气象站的分布见图 2。

1.2 基于光流法雷达外推的降水预报方案

(1) 光流法求雷达回波移动矢量场。光流法研究的是三维图像在二维平面投影时图像灰度在时间上的变化与图像结构及运动的关系，实质是由二维光流场重构三维运动场，根据Gibson (1950)提出的原始光流方程

$ {I_x}u + {I_y}v + {I_t} = 0 $

(1)

其中：${I_x} = \frac{I}{X}, {I_y} = \frac{I}{Y}, {I_t} = \frac{I}{T}, u = \frac{{{\rm{d}}x}}{{{\rm{d}}t}}, v = \frac{{{\rm{d}}y}}{{{\rm{d}}t}}$。雷达图像上，I_x、I_y为图像点灰度的空间梯度，I_t为图像点灰度的时间变化率(u，v)即为光流场。I_x、I_y、I_t可以通过相邻的图像点灰度计算，而(1)式中存在u、v两个变量，不加约束条件无法求解。常见有两种增加约束条件的方法，即全局平滑约束的HS法和局部平滑约束的LK法。

① 全局平滑约束的HS法。HS法中认为同一运动物体的光流场连续及平滑，因此构建以下灰度全局约束方程

$ J = {J_0} + \lambda {J_{HS}} $

(2)

$ {J_0} = \iint {({I_x}u + {I_x}v + {I_t}){\text{d}}x{\text{d}}y} $

(3)

$ {J_{HS}} = \iint {\left[ {{{\left({\frac{{\partial u}}{{\partial x}}} \right)}^2} + {{\left({\frac{{\partial u}}{{\partial y}}} \right)}^2} + {{\left({\frac{{\partial v}}{{\partial x}}} \right)}^2} + {{\left({\frac{{\partial v}}{{\partial y}}} \right)}^2}} \right]}{\text{d}}x{\text{d}}y $

(4)

式中: λ是平滑系数(λ > 0)，J₀是灰度守恒项(数据项)，J_HS是约束项(平滑项)。利用欧拉-拉格朗日方法可求解方程，数值解可用雅克比迭代法求解。

② 局部平滑约束的LK法。而LK法则假定小区域Ω的光流维持恒定不变，即在局部补充 n个方程，由式(1)转换为

$ \left[ \begin{gathered} {I_{x1}}\;\;\;\;{I_{y1}} \hfill \\ {I_{x2}}\;\;\;\;{I_{y2}} \hfill \\ \vdots \hfill \\ {I_{xn}}\;\;\;\;{I_{yn}} \hfill \\ \end{gathered} \right]\left[ \begin{gathered} u \hfill \\ v \hfill \\ \end{gathered} \right] = \left[ \begin{gathered} - {I_{t1}} \hfill \\ - {I_{t2}} \hfill \\ \vdots \hfill \\ - {I_{tn}} \hfill \\ \end{gathered} \right] $

(5)

当n>2时, 式(5)是超定方程，可用最小二乘法求解。若假定的小区域Ω内使用一个窗口权重函数W，使得靠近中心区域的影响比其他范围大，得到的运动矢量场则为

$ \left[ \begin{gathered} u \hfill \\ v \hfill \\ \end{gathered} \right] = \left[ \begin{gathered} \sum {{W^2}I_{xi}^2} \;\;\;\;\;\;\;\sum {{W^2}{I_{xi}}{I_{yi}}} \hfill \\ \sum {{W^2}{I_{xi}}{I_{yi}}} \;\;\;\;\sum {{W^2}I_{yi}^2} \hfill \\ \end{gathered} \right]\left[ \begin{gathered} \sum {{W^2}{I_{xi}}{I_{ti}}} \hfill \\ \sum {{W^2}{I_{yi}}{I_{ti}}} \hfill \\ \end{gathered} \right] $

(6)

③ 改进变分法。近年来基于变分建模逐渐成为当前主流的光流计算方法(柳士俊和张蕾，2015)，而变分光流计算就是最小化某个能量泛函的过程。而通过建立数据项和平滑项的卷积形式，将HS、LK的优点结合起来，使既满足光滑、又能克服噪声，呈现鲁棒性。将数据项、平滑项进行多种组合，并结合卷积形式，可以统一绝大部分光流算法。本文采取王志斌等(2019)的改进变分光流法(以下简称为光流法)，即对(2)、(5)式进行组合，把矢量(u，v，1)、灰度矢量I通过向量相乘得到(7)式，并加入变分约束项，构建如(8)式所示的变分光流能量函数，用数值方法求解其极小值即可。

$ \begin{gathered} {W^T}{J_\rho }({\nabla _3}F)W = (u(x, y), v(x, y), 1)\left(\begin{gathered} {f_x} \hfill \\ {f_y} \hfill \\ {f_t} \hfill \\ \end{gathered} \right) \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;({f_x}, {f_y}, {f_t})\left(\begin{gathered} u(x, y) \hfill \\ v(x, y) \hfill \\ \;\;\;\;1 \hfill \\ \end{gathered} \right) \hfill \\ \end{gathered} $

(7)

$ \begin{array}{l} E(u, v) = \int\limits_\Omega {\left\{ {{W^T}{J_\rho }({\nabla _3}F)W + \alpha } \right.} \cdot \left[ {{{\left({\frac{{{\partial ^2}u}}{{\partial {x^2}}}} \right)}^2} + {{\left({\frac{{{\partial ^2}u}}{{\partial {y^2}}}} \right)}^2} + } \right.\\ \left. {\left. {2{{\left({\frac{{{\partial ^2}u}}{{\partial x\partial y}}} \right)}^2} + {{\left({\frac{{{\partial ^2}v}}{{\partial {x^2}}}} \right)}^2} + {{\left({\frac{{{\partial ^2}v}}{{\partial {y^2}}}} \right)}^2} + 2{{\left({\frac{{{\partial ^2}v}}{{\partial x\partial y}}} \right)}^2}} \right]} \right\}{\rm{d}}x{\rm{d}}y \end{array} $

(8)

式中, F(x，y，t) 是雷达图像序列，x、y在Ω内；f_x、f_y、f_t为光流在x、y方向及沿时间t的变化；向量W (x，y) = (u(x, y)，v(x, y)，1)^T；▽₃F =（f_x, f_y, f_t）^T为光流梯度向量；向量J_ρ(▽₃F) = K_ρ*▽₃F▽₃F^T，* 为卷积，K _ρ为标准差, 为ρ的高斯分布；α >0。ρ→0，可归为HS方法；α → 0，即为LK方法。本文中，α取2 700，ρ取1.8。

(2) 雷达回波与降水强度的转换。雷达回波对应的降水计算主要采用基于准同雨团样本概念雷达和雨量计的实时同步结合方法(RASIM方法)(万玉发等, 2008)，用同步积分使雷达和自动气象站降水采样为准同雨团样本，建立雷达回波与降水的动态转换Z-R关系。

(3) 降水临近预报。改进王珏等(2008)提出的多尺度合成降水临近预报技术，使用光流法代替相关法求雷达回波速度，采用半拉格朗日法进行回波降水外推预报。通过β-γ尺度滤波、光流法计算回波移动速度矢量、γ尺度回波移速处理后，再采取四项处理：①用Z-R关系实现回波转换降水强度；②用半拉格朗日法进行各个尺度的回波降水强度外推预报；③用轨迹象元瞬时摄像玷染求和法(TPIS)(万玉发等, 1998)求累计降水；④对几个尺度外推的降水量结果进行叠加并取最大值，从而得到各个预报时效的降水量计算结果。

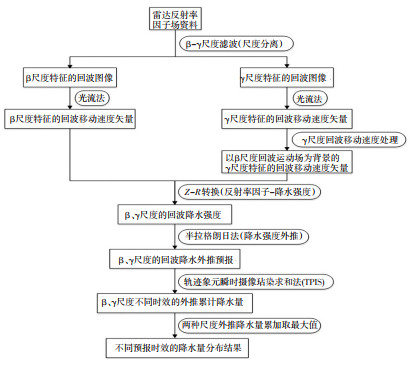
基于光流法的降水预报方案流程如图 3所示。

1.3 检验方案

主要基于质量较好的736个国家气象站、格点实况降水，对基于光流法的雷达外推降水临近预报值结果进行检验，检验方案如下：

(1) 分级及累加定量降水检验。根据降水量(R)的大小，分级降水检验分别按照0.1 mm≤R≤2.9 mm、3.0mm≤R≤9.9mm、10.0mm≤R＜≤19.9mm、20.0mm≤ R≤49.9 mm、R≥50 mm不同降水量级分别检验。

(2) 分时段外推预报检验。针对外推预报0~3 h及0~1 h、1~2 h、2~3 h的结果分别检验。

(3) 站点邻域法检验。对国家气象站周边一定范围的格点降水外推预报进行检验，即在雨量站周边4个点(含该点)外推预报值与气象站雨量测量值绝对误差最小的数值作为该点外推预报的降水值，该站点外推预报值与国家气象站站点实况值对比进行降水检验。以下相关检验简称“站点-格点”检验。

(4) 格点邻域法检验。不对外推预报和融合降水实况格点进行严格的一对一匹配，而是依据外推预报格点为中心的一定范围内是否出现评定的事件的融合降水实况格点来评定该格点外推预报正确。划定10 km为扫描半径范围。以下相关检验简称“格点-格点”检验。

(5) 检验指标包括TS评分、平均误差、平均绝对误差率、均方根误差。

其中TS评分的计算公式为

$ T{S_k} = \frac{{N{A_k}}}{{N{A_k} + N{B_k} + N{C_k}}} $

(9)

式中NA_k为预报正确的站(次)数、NB_k为空报站(次)数、NC_k为漏报站(次)数，k为1~5，分别代表各级降水。

2 结果分析 2.1 降水分级样本分析

降水分级检验评定标准见表 2。2020年6—8月长江流域17次降水过程中，1 h累计雨量≥20 mm、≥50 mm的样本数分别为2 838个、159个，最大1 h累计雨量134.6 mm，8月11日02时出现在长江上游岷江四川芦山站。3 h累计雨量≥20 mm、≥50 mm样本数分别为14 844个、2 029个，3 h最大累计雨量324.2 mm，8月11日02时也出现在岷江四川芦山站。736个国家气象站参与检验的1 h、3 h累计雨量≥0.1 mm分级样本数分别如表 3、表 4所示。

2.2 “站点-格点”分级降水预报TS检验

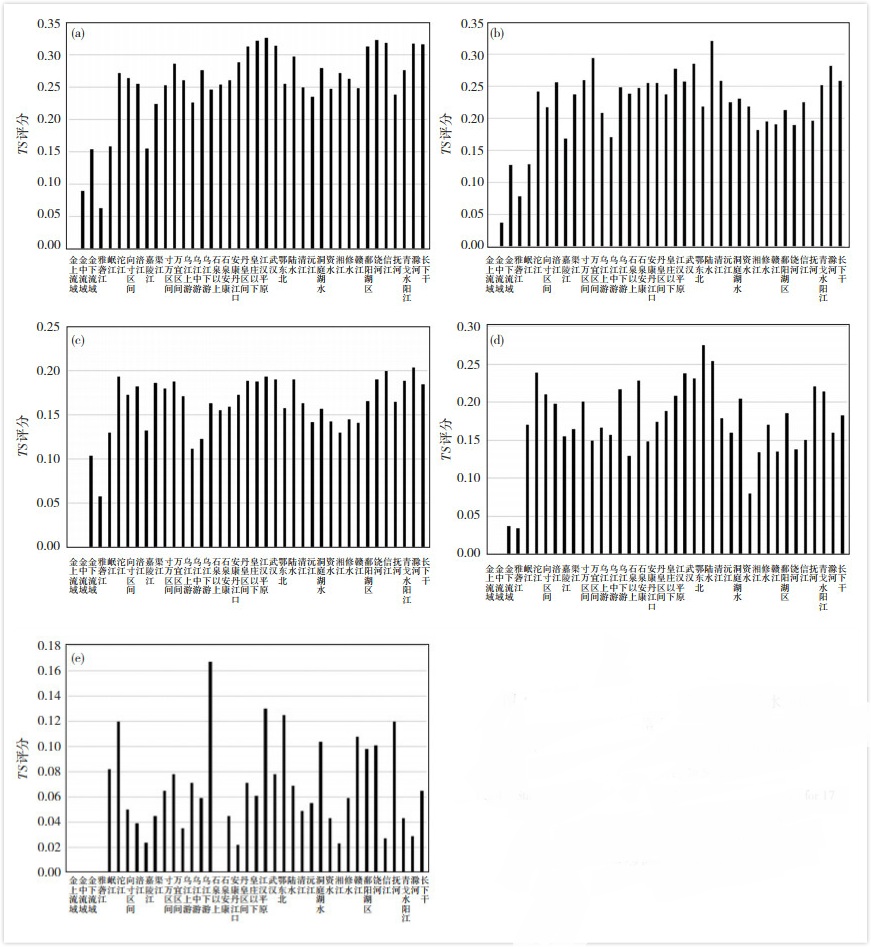
应用736个国家气象站评估光流法临近降水预报的结果，图 4给出了长江流域39分区17次过程“站点-格点”检验方案0~3 h的TS评分结果，从图中可以看出：

(1) 光流法的临近预报在不同流域分区的TS评分，与雷达及雨量站分布存在较大的相关性。雷达及雨量站分布较为稀疏的金沙江上游和中游、雅砻江等子流域，光流法的临近预报TS评分较低，50 mm以下各个分级评分结果，金沙江上游为0，金沙江中游、雅砻江均在0.08以下；而雷达及雨量站分布较密集的长江中下游各子流域，TS评分相对较高，0.1~2.9 mm、3~9.9 mm、10~19.9 mm、20~49.9 mm量级降水TS评分，岷江以东的各分区绝大多数均超过0.1，其中0.1~ 2.9 mm量级TS评分最高的武汉流域为0.33，3~9.9 mm量级TS评分最高的清江流域为0.32，10~19.9 mm量级最高的滁河流域为0.2，20~49.9 mm量级，最高的滁河流域为0.28。TS评分与雷达及雨量站分布呈正相关，雷达及雨量站分布越稀疏的流域，评分越低。

(2) 不同流域分区的TS评分，与洪水过程降水落区分布有一定关联。在不考虑雷达覆盖不足的金沙江、雅砻江、岷江、嘉陵江几个子流域情况下，洪水过程总体降水相对集中区主要位于沱江、涪江以及长江干流附近的乌江下游、万州-宜昌、清江、澧水、江汉平原、皇庄以下、武汉、鄂东北、修水、鄱阳湖区、饶河、青弋水阳江、长下干等子流域，以上子流域在0.1~2.9 mm、3~ 9.9 mm、10~19.9 mm、20~49.9 mm各个量级中均处于相对高分区，0.1~2.9 mm量级TS评分均在0.25~0.33，3~9.9 mm量级TS评分均在0.19~0.32，10~19.9 mm量级TS评分均在0.14~0.21，20~49.9 mm量级TS评分均在0.14~0.28。降水相对偏少的乌江上中游、石泉以上、安康-丹江口、资水、湘江多离长江干流较远，呈现有相对低分的情况，如3~9.9 mm量级乌江中游、资水TS评分为0.17和0.18，10~19.9 mm量级乌江中游TS评分为0.11，20~49.9 mm量级资水TS评分低至0.08。

(3) 对极端强降水的预报上，光流法有一定的降水预报表现。从≥50.0 mm量级TS评分来看，超过0.1有沱江、石泉以上、武汉、陆水、洞庭湖区、赣江、饶河、抚河8个子流域，这表明光流法的临近预报对这些子流域的极端降水预报效果较好，对长江流域中小河流洪水预报有较高的参考价值。

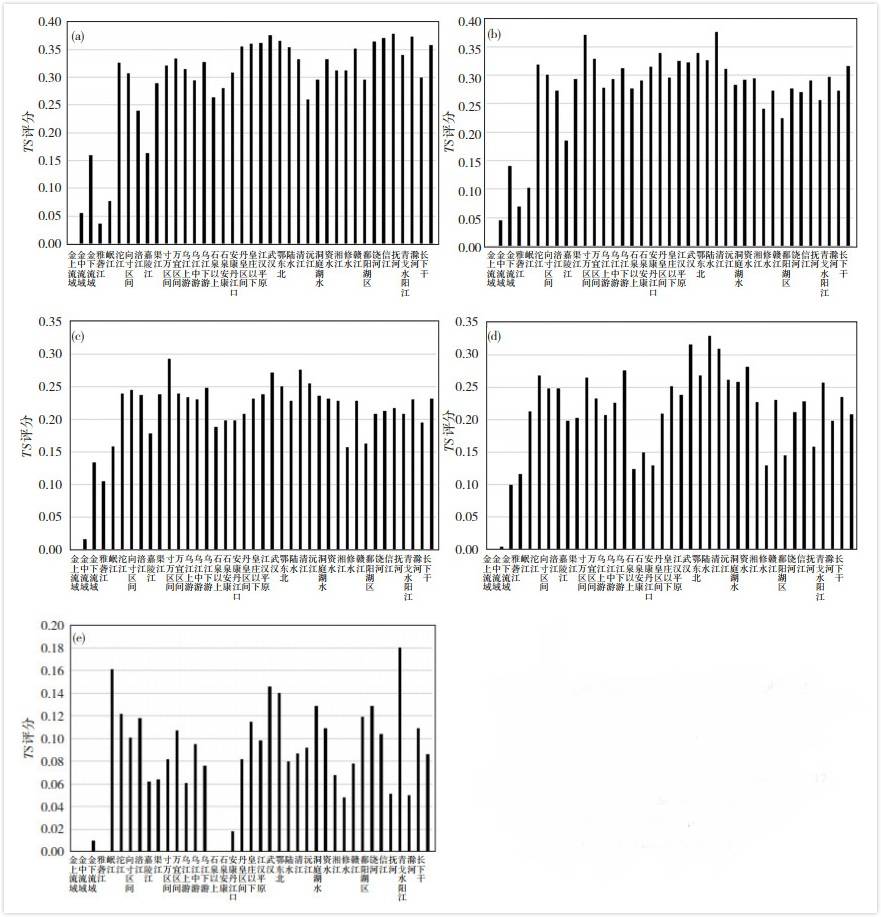
2.3 “格点-格点”分级降水预报TS检验

应用格点实况降水评估光流法临近降水预报的结果，图 5给出了长江流域39分区17次过程“格点-格点”检验方案0~3 h的TS评分结果，可以看出其与“站点-格点”检验方案的结果存在一定的相似性：

(1)“格点-格点”方案的TS评分也与雷达及雨量站分布存在较大的相关性。雷达及雨量站分布较为稀疏的金沙江上游和中游、雅砻江等子流域，光流法的临近预报TS评分较低，20 mm以下各个分级评分结果，金沙江上游为0，金沙江中游、雅砻江均在0.07以下，20~49.9 mm雅砻江提高至0.11~0.12，金沙江上游、中游仅为0~0.01；而雷达及雨量站分布较密集的长江中下游各子流域，TS评分相对较高，0.1~2.9 mm、3~9.9 mm、10~19.9 mm、20~49.9 mm量级降水TS评分岷江以东的各分区，绝大多数均超过0.13，其中0.1~2.9 mm最高的信江为0.38，3~9.9 mm最高的清江为0.38，10~19.9 mm最高的寸滩-万州为0.29，20~ 49.9 mm最高的陆水为0.33，均较“站点-格点”方案有所提高。

(2) 在不考虑雷达覆盖不足的金沙江、雅砻江、岷江、嘉陵江几个子流域情况下，“格点-格点”方案的TS评分，也与洪水过程降水落区分布有关。洪水过程总体降水相对集中区主要位于沱江、涪江以及长江干流附近的各个子流域在3~9.9 mm、10~19.9 mm、20~ 49.9 mm各个量级中均处于相对高分区，3~9.9 mm量级TS评分均在0.27~0.38，10~19.9 mm量级TS评分均在0.20~0.29，20~49.9 mm量级TS评分均在0.20~ 0.33。降水相对偏少的乌江上中游、石泉以上、安康- 丹江口、资水、湘江多离长江干流较远，呈现有相对低分的情况，如3~9.9 mm量级赣江、湘江TS评分为0.23和0.24，10~19.9 mm量级湘江、赣江TS评分为0.15和0.16，20~49.9 mm量级石泉以上、安康-丹江口、湘江TS评分低至0.12、0.13、0.13，但相对较“站点-格点”方案有所提高。

(3) 对极端强降水的预报上，光流法有较好的降水预报表现。从≥50.0 mm量级TS评分来看，除石泉以上、安康-丹江口、陆水外其他子流域的TS评分均较“站点-格点”方案有明显提高。超过0.1的有岷江、沱江、向家坝-寸滩、涪江、万州-宜昌、皇庄以下、武汉、鄂东北、沅江、洞庭湖区、赣江、鄱阳湖区、饶河、抚河、滁河14个子流域，较“站点-格点”方案增加6个子流域，对实况降水的相对强中心区域能够有更好的表现。

(4) 与“站点-格点”降水预报检验TS结果相比，基于格点实况降水的“格点-格点”降水预报检验结果在各个量级上均有明显提高，这是由于融合了雷达和卫星资料的格点实况降水能够填补站点稀疏地区的降水盲区，而且格点实况降水落区相对平滑，更能表征大范围降水落区分布特征。

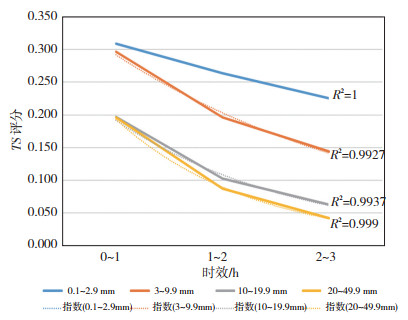
2.4 不同时效TS评分结果

通过以上分析，可以看到基于格点实况降水的格点-格点降水预报检验结果在绝大多数量级上均有明显提高，同时格点实况降水落区相对平滑，更能表征大范围降水落区分布特征，因此选择应用“格点-格点”检验方法来评估0~1 h、1~2 h、2~3 h各个时效的临近预报效果。应用格点实况降水降水检验不同预报时效光流法临近预报能力，图 6给出了2020年长江流域17次过程不同时效光流法临近预报“格点-格点”检验方案的TS评分。从图中可以看出：各个量级降水光流法临近预报的准确率在1 h以后快速下降, 随预报时效的变化准确率基本上是以指数规律递减的，且不同量级降水的R平方值均大于0.99。

2.5 误差分析

应用格点实况降水来分析光流法0~3 h临近降水预报在2020年长江流域17次降水过程的全流域预报误差，包括平均误差、平均绝对误差、平均绝对误差率、均方根误差(见表 5)。

从长江流域光流法临近降水预报检验结果分析可知，平均误差上，预报结果较格点实况降水在0.1~ 9.9 mm级别基本相近，10.0 mm以上级别预报结果整体偏大，其中10.0~19.9 mm级别上预报结果偏大1 mm，20.0~49.9 mm级别上预报结果偏大近5 mm，≥50.0 mm级别上预报结果仅偏差0.25 mm；平均绝对误差上，预报结果较格点实况降水在0.1~9.9 mm级别基本相近，10.0 mm以上级别预报结果整体偏差，其中10.0~ 19.9 mm级别上预报结果偏差近8 mm，20.0~49.9 mm级别上预报结果偏差近18 mm，≥50.0 mm级别上预报结果偏差近38 mm；对于平均绝对误差率上，预报结果较格点实况降水在0.1~9.9 mm级别误差率约为1.6%，3.0~9.9 mm级别误差率约为4.1%，10.0~19.9 mm级别上误差率约为6.0%，20.0~49.9 mm级别上误差率约为7.3%，≥50.0 mm级别上误差率约为10.3%，即10.0 mm以下误差率在5%以内，10.0 mm以上级别误差率约为6~11%；均方根误差上，在0.1~9.9 mm级别均方根误差约为0.9 mm，3.0~9.9 mm级别均方根误差约为4 mm，10.0~19.9 mm级别上均方根误差约为10 mm，20.0~49.9 mm级别上均方根误差约为22 mm，≥50.0 mm级别上均方根误差约为44.1 mm。随着降水量级的增大，平均绝对误差、平均绝对误差率、均方根误差均呈现逐渐增大的趋势。

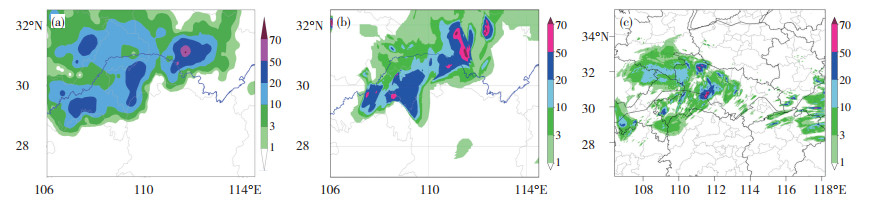
选取2020年6月27日11—14时这一时间段的3 h累计雨量(图 7)，比较实时业务中光流法雷达外推、武汉RUC快速循环同化模式(2020年6月27日08时起报)预报效果。实况显示此时间段长江流域主要强降水落区位于四川东部、重庆南部和湖北西南部、湖北西部四个强降水中心，最强中心湖北西部当阳3 h累计雨量多站超过150 mm。可以看到，除四川东部外，光流法雷达外推预报出了其他三个中心，而快速循环同化模式仅预报出了湖北西部的强降水中心，光流法雷达外推在0~3 h临近预报上要好于快速循环同化模式。

由于光流法临近降水预报与三源格点实况降水产品各级别的平均绝对误差率仅为1.6%~10.3%，且要优于数值模式预报。因此，在流域水文气象预报业务上，可考虑将光流法0~3 h临近降水预报结果应用于长江流域定量降水预报，代替目前直接使用的数值模式输出结果。

3 结论

通过利用长江流域组网雷达和自动气象站逐小时降水观测资料，建立了基于变分光流法的长江流域雷达外推降水预报产品，并计算出了2020年17次长江洪水天气过程的0~3 h 39分区TS检验结果和全流域偏差分析结果，得到以下主要结论：

(1) 光流法0~3 h临近预报TS评分表明，该方法对雷达分布较为密集的长江上游东部和长江中下游评分较高、预报结果较为精准，对雷达覆盖不足或因周边山脉遮挡较为明显的长江上游西部地区评分较低、结果较差。

(2) 光流法0~3 h临近预报在不同流域分区的TS评分与洪水过程降水落区分布有关，降水的集中区，同样也是临近预报TS评分的相对高分区，表明该方法能够较好的追踪降水天气系统移动演变。在极端强降水的预报上，该方法也有较好的预报表现。

(3) 光流法0~1 h、1~2 h、2~3 h临近预报，以0~1 h预报准确率最高、可用性最高，其预报效果随着预报时效的变化以指数规律递减。

(4) 光流法0~3 h临近降水预报结果较格点实况降水，10.0 mm以下的降水基本接近，绝对误差率在5%以内；10.0 mm以上级别，其绝对误差率为6%~ 11%。随着降水量级的增大，平均绝对误差、平均绝对误差率、均方根误差均逐渐增大。

(5) 在流域水文气象预报业务上，将光流法0~3 h临近降水预报结果应用于长江流域定量降水预报，代替目前直接使用的数值模式输出结果，对提高洪水预报精度有较强的实用意义。