2. 上海市气候中心, 上海 200030
2. Shanghai Climate Center, Shanghai 200030
空气动力学参数如粗糙度(z0)和零平面位移(zd)是研究地气相互作用的重要参数之一,对天气系统具有扰动影响(赵鸣,2008;熊仕焱等,2010;琚陈相等,2014),因此在数值模式参数化中也具有重要意义。其计算方法主要有基于风或湍流观测数据的动力学方法,以及基于研究区域下垫面粗糙元几何形态特征的形态学方法。动力学方法是最传统的空气动力学参数计算方法,基于风杯风速计等低频观测仪器,可以利用近中性层结下近地面风廓线外推,如Grimmond等(1998)基于多层风观测资料计算美国芝加哥梯度观测铁塔附近区域的粗糙度;或基于单层风观测资料,使用风向风速标准差法(WMO,2006)计算强风状态下的z0,如张文昱等(2009, 2011)、胡文超等(2010)计算黄土高原和河西走廊非均一下垫面的z0。对于具备超声风速计等高频观测仪器的研究区域,单一高度观测数据即可同时求解z0和zd,如张宏升等(1997)、高志球等(2002)、周艳莲等(2007)、鞠英芹(2012),唐玉琪等(2016)利用温度脉动相关法、Martano方法(Martano, 2000)和涡动相关法(Grimmond, 1998)分别计算北京325 m气象铁塔、长白山森林观测塔和上海徐家汇铁塔附近区域的空气动力学参数。但动力学方法对观测条件要求较高(需架设高塔或安装超声风速计),或应用条件有限制(如部分方法需要选用近中性或不稳定层结数据),同时观测数据也因数据质量、天气条件等原因,无法保证每个风向都有足够的数据样本用于计算,这一缺点在城市区域尤为明显。
基于下垫面粗糙元形态特征的形态学方法,使观测条件不足区域的空气动力学参数计算成为可能。粗糙元种类、大小、形状及排列方式等都直接影响地面粗糙度性质(刘小平等,2003),国内外学者根据各自研究区域的粗糙元特征,发展了多种计算方法:从最初基于建筑高度的简单系数计算方法(如z0=0.1zH),形态学方法经历了观测技术进步和计算方法丰富和完善,逐渐成为计算大区域空气动力学参数的重要手段。Grimmond等(1999)使用多种形态学方法计算了北美7座城市的11个研究区域的空气动力学参数,并与动力学方法计算结果进行对比,并认为Raupach (1994)提出的方法(简称为Ra方法)较为合理;尽管不同方法结果差异较大,但为城市下垫面空气动力学参数估算的新思路开拓打下基础。高志球等(2002)利用单一高度超声风速仪风温资料计算中科院大气物理所气象铁塔附近非均匀下垫面z0,并与Grimmond研究结果进行对比,对多种形态学方法的验证和发展具有重要意义。Macdonald等(1998)认为交错、非均匀分布的粗糙元产生的阻力比均匀分布时更大,因此在Lettau风廓线关系基础上,进一步引入粗糙元顶面积系数、迎风面积系数,并改进粗糙元拖曳系数,使计算方法(简称为Ma方法)对粗糙元密度高、分布不均匀特性更敏感。Kanda等(2013)提出了同时考虑最大建筑高度、建筑高度标准差、平均建筑高度、迎风面积系数和顶面积系数的更为复杂的形态学计算方法(简称为Ka方法),并在日本东京和名古屋的真实下垫面及模型下垫面的实验中均取得较好效果。粗糙元高度变化对气流和湍流特性的影响,如较高的粗糙元对气流能产生不成比例的阻力越来越受到关注(Mohammad et al., 2015)。Kent等(2017)在伦敦进行了动力学与形态学、不同形态学方法之间计算结果差异对比,认为计算中考虑最大建筑高度、建筑高度标准差的方法更适合粗糙元交错排列的复杂下垫面计算。但由于动力学方法对局地动力、热力条件普遍的敏感性,以及不同形态学方法计算时所考虑的粗糙元几何形态、分布参数差异,关于不同特征下垫面上形态学计算方法的适用性,目前还没有较一致的结论。因此,继续开展复杂下垫面动力学参数形态学计算方法的适应性研究具有重要意义。
目前,国内复杂下垫面空气动力学参数形态学计算方法的研究较少,唐玉琪等(2016)利用上海徐家汇铁塔的单层风温观测数据(包括风杯风速计和超声风速计)、铁塔周围半径500 m范围内的下垫面粗糙元特征参数,分别使用动力学和形态学方法进行了空气动力学参数计算。结果表明,在以上海徐家汇地区为例的典型特大城市复杂下垫面上,动力学方法和形态学方法计算结果差异较大。上述结论仅为徐家汇一个研究区域的分析结果,为进一步验证形态学方法在上海多样性下垫面的适用情况,确定最适合上海下垫面的形态学计算方法,本文选取上海奉贤、青浦、宝山铁塔附近半径1 km范围为研究区域,利用的长时间序列铁塔梯度观测数据和高分辨率的下垫面粗糙元信息,以动力学方法(Lettau风廓线方法,简称为Lw方法)计算结果为参考值,对比经验系数法(Rule of thumb,简称为Rt方法)、Ra方法、Ma方法和Ka方法的计算结果,分析上述形态学方法主要影响因子,讨论形态学方法在上海典型城市下垫面的适用性,进而确定最适合上海空气动力学参数计算的形态学方法。
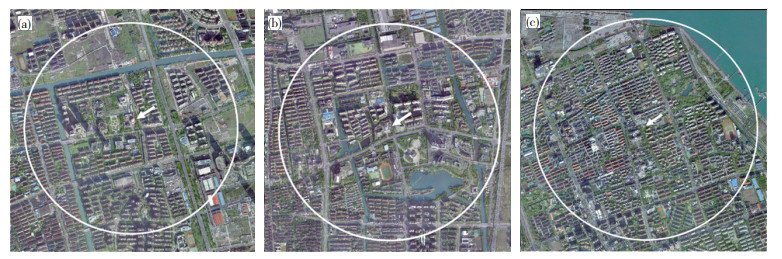
1 资料来源 1.1 研究区域上海城市下垫面不仅包含如徐家汇研究区域(唐玉琪等,2016)这样高楼林立的商业中心,还有建筑高度变化稍小的商住混合次中心地区和建筑排列较整齐、密集的居民区。因此,结合现有的根据国家地理信息公共服务平台数据、高清卫星数据融合资料和实地考察结果,并考虑铁塔梯度观测条件,确定上海奉贤、青浦和宝山三座梯度观测铁塔周围半径1 km范围为本文研究区域(下文简称为研究区域),从图 1可见,研究区域内多为7层左右商住混合区,分散分布12层以上高层建筑;植被主要为道路绿化、草坪等;与奉贤、青浦相比,宝山研究区域以居民小区为主,建筑排列较整齐,但也更密集。综上所述,三个研究区域均呈现建筑林立而植被覆盖较少、典型的城市非均一下垫面特征。此外,上述三个研究区域的梯度观测系统于2010年完成设备建设,进入组网观测阶段,并分别于2013年和2017年进行了观测仪器维护,具有较长时间序列、可靠的观测数据。
|
图 1 研究区域奉贤(a)、青浦(b)、宝山(c)铁塔附近建筑和植被分布情况(其中白色箭头指示铁塔位置,白色实线圆圈示意以铁塔为中心、半径1 km的范围) Fig. 1 Building and vegetation distribution of measurement sites at (a) FX, (b) QP and (c) BS. (White arrows point location of towers, and white solid line circles indicate areas with a 1000 m radius centered on a tower) |
上海梯度观测铁塔均以电视铁塔为载体,观测高度统一设置为5层(即10 m、30 m、50 m、70 m、100 m),其中风向、风速5层,气温2层(10 m、70 m),相对湿度1层(10 m)。观测硬件设备为无锡无线电科学研究所有限公司生产的ZQZ-NT系列梯度观测系统,供电方式为交流220 V,所有的站点均采用GPRS通信方式,数据观测频率为1次·min-1。采用统一型号的传感器,其中,三杯风速计型号为ZQZ-TF(江苏省无线电研究所),最小启动风速0.3 m·s-1,分辨率0.1 m·s-1;气温传感器型号为HMP45D/Pt100,测量范围为-50~50 ℃,分辨率为0.1 ℃;相对湿度传感器型号为HMP45D,分辨率为1%。
1.2 数据说明和质量控制动力学方法计算下垫面空气动力学参数选用三个研究区域2012—2014年梯度观测2 min平均风向、风速、气温观测数据。为使计算结果合理,选用三杯风速计风速大于2 m·s-1、气温在[-5 ℃, 42 ℃]区间的观测资料,并剔除缺测和僵直数据,其中风向平均采用单位矢量法(邱传涛等,1997)。同时,为排除邻近建筑的影响,统一选择50 m、70 m和100 m高度观测数据用于空气动力学参数计算;考虑到研究区域下垫面的非均一性,以铁塔为中心划分2°间隔的风向区间进行计算。由于上海各梯度观测铁塔区域植被覆盖率较低,且多为人工植被,季节变化小,因此本文计算中忽略季节变化影响。
形态学方法计算数据包括:(1)地表分类数据:国家地理信息公共服务平台(https://www.tianditu.gov.cn/),高清卫星数据融合资料(高分辨率商业遥感卫星Quick Bird,水平分辨率0.6 m)和实地考察;(2)地面高程信息:上海市测绘院建筑矢量地图数据和实地调研。地表分类数据结合地面高程信息,通过ARCMAP、QGIS等软件建立数字表面模型(Digital Surface Model,DSM),再使用Python语言计算得到铁塔为中心、半径1 km研究区域内2°间隔风向区间的建筑平均高度(zH)、建筑高度标准差(σH)、最大建筑高度(zHmax)、迎风面积系数(λF)和顶面积系数(λP)等,具体计算方法将在2.2节中进行介绍。
2 空气动力学参数计算方法空气动力学参数的定义和物理意义基于对近地面风速垂直分布的研究。其中,下垫面粗糙度z0是对数风廓线公式(略)中平均风速(u)等于零的高度;而在森林、城镇建筑物上空等条件下,对数风廓线公式需要做出一定修正,此时下垫面的起始高度将被抬高至森林、建筑物顶层附近,即以z-d值替换对数风廓线公式中的z值得到式(1),此d值即称为动力学零值位移,即零平面位移zd,其物理意义是气流与下垫面的作用相当于发生在这一高度上,粗糙度也变成是这一高度之上的物理属性。
| $ \frac{{\bar u}}{{{u_*}}} = \frac{1}{k}{\rm{ln}}\frac{{z - d}}{{{z_0}}} $ | (1) |
目前,基于铁塔风温观测数据的动力学计算方法仍是下垫面动力学参数研究的常用方法,国内森林、沙漠、农田和城市地区的粗糙度分析研究中均有应用。因此,本文将动力学方法作为参照,对形态学方法的计算结果进行对比分析。
2.1 动力学方法上海奉贤、青浦和宝山梯度观测铁塔均为慢响应观测仪器(即原始数据观测频率为1次·min-1)的多层观测,因此本文的动力学方法选用Lw方法(Lettau, 1957):以相似理论为基础,在近中性条件下,利用多层的风温资料进行空气动力学参数估算。首先Lettau引入零点位移D(zero-displacement)的概念,并认为D = z0 - zd;D的求解方法如下
| $ \sum\nolimits_{i = 1}^N {{\epsilon ^2}} = \sum\nolimits_{i = 1}^N {{{\left\{ {({U_i} - \overline {{U_N}} ) - \frac{{{u_*}}}{k}\left[ {{\rm{ln}}({z_{si}} + D) - \overline {{\rm{ln}}({z_{si}} + D)} } \right]} \right\}}^2}} $ | (2) |
| $ \frac{{{u_*}}}{k} = \frac{{\sum\nolimits_{i = 1}^N {({U_i} - \overline {{U_N}} )} [{\rm{ln}}({z_{si}} + D) - \overline {{\rm{ln}}({z_{si}} + D)} ]}}{{\sum\nolimits_{i = 1}^N {{{[{\rm{ln}}({z_{si}} + D) - \overline {{\rm{ln}}({z_{si}} + D)} ]}^2}} }} $ | (3) |
其中,zsi为第i层观测高度,Ui为zsi高度风速,N为观测层数(Lettau建议至少有3~4层观测),u*为摩擦速度(下同),k=0.4为Von-Karman常数(下同),上划线表示N层之平均值。当式(2)左侧差值ε平方和最小时,对应的D即为所求;进而可通过式(3)求得u*/k。将D和u*/k带入近中性条件下风速的对数廓线公式,并利用D = z0 - zd关系,则可以求得空气动力学参数
| $ {{z_{0L}} = ({z_s} + D){\rm{exp}}\left( { - \frac{{{U_Z}k}}{{{u_*}}}} \right)} $ | (4) |
| $ {{z_{dL}} = {z_{0L}} - D} $ | (5) |
其中z0L、zdL下标字母L表示Lw方法的计算结果,本文其它计算方法的结果采用相同标记方法。上述动力学方法需选用近中性条件下的观测数据,因此计算前需要进行观测高度附近大气稳定度判定。本文用铁塔10 m和70 m的风向、风速和气温观测资料计算梯度理查森数Ri,当|Ri| < 0.1时视大气稳定度状态为近中性
| $ Ri = \frac{g}{{\bar T}}\frac{{\Delta \bar T/\Delta z}}{{{{(\Delta \bar u/\Delta z)}^2}}} $ | (6) |
其中,g = 9.8 m·s-1为重力加速度,T为气温,z为观测高度,△为两观测高度之差。
2.2 形态学计算方法形态学方法不依赖铁塔的风温观测数据,以下垫面粗糙元的几何形态特征参数建立方程,综合考虑粗糙元高度及其变化率、粗糙元密度和排列方式等,求解空气动力学参数,在无观测条件或大范围研究区域的下垫面空气动力学参数计算中具有明显优势。本文以上海奉贤、青浦和宝山铁塔附近半径1 km范围为研究区域,由于三个研究区域均为城市下垫面特征,植被主要为道路绿化、草坪等,因此,粗糙元统计对象为研究区域内的建筑,具体参数包括建筑高度、建筑高度标准差、最大建筑高度、迎风面积系数和顶面积系数等,分别用Rt方法、Ra方法(Raupach et al., 1994)、Ma方法(Macdonald et al., 1998)和Ka方法(Kanda et al., 2013)计算各个风向区间的空气动力学参数。各方法对计算参数的需求情况如表 1所示:
|
|
表 1 形态学计算方法参数需求情况 Table 1 Morphometric methods with their required geometric parameters |
其中,经验系数方法最为简单,只需已知粗糙元高度(
| $ {{z_d} = 0.7\overline {{z_H}} } $ | (7) |
| $ {{z_0} = 0.1\overline {{z_H}} } $ | (8) |
基于Ra方法(Raupach,1994)在粗糙下垫面拖曳作用和区划研究基础上,提出了基于粗糙元高度及迎风面积系数的计算公式
| $ {\frac{{{z_{dR}}}}{{{z_H}}} = 1 + \left\{ {\frac{{{\rm{exp}}[ - {{({c_{d1}}2{\lambda _F})}^{0.5}} - 1]}}{{{{({c_{d1}}2{\lambda _F})}^{0.5}}}}} \right\}} $ | (9) |
| $ {\frac{{{z_{0R}}}}{{\overline {{z_H}} }} = \left( {1 - \frac{{{z_{dR}}}}{{\overline {{z_H}} }}} \right){\rm{exp}}\left\{ { - k\frac{U}{{{u_*}}} + {\psi _h}} \right\}} $ | (10) |
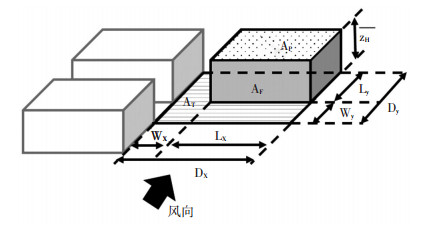
其中,zdR和z0R分别为Ra方法计算的零平面位移和粗糙度,ψh=0.193为粗糙子层影响函数(Raupach,1994),cd1=7.5为自由系数,λF=AF/AT为建筑迎风面积系数(其中,AF = Lx ×
|
图 2 形态学计算方法面积参数定义示意图 Fig. 2 The definition of surface dimensions used in morphometric methods |
Ma方法(Macdonald et al., 1998)则进一步引入粗糙元顶面积系数λP控制
| $ {\frac{{{z_{dM}}}}{{\overline {{z_H}} }} = 1 + {\alpha ^{ - {\lambda _p}}}({\lambda _p} - 1)} $ | (11) |
| $ {\frac{{{z_{0M}}}}{{\overline {{z_H}} }} = \left( {1 - \frac{{{z_{dM}}}}{{\overline {{z_H}} }}} \right){\rm{exp}}\left[ { - {{\left\{ {0.5\beta \frac{{{C_{1b}}}}{{{k^2}}}\left( {1 - \frac{{{z_{dM}}}}{{\overline {{z_H}} }}} \right){\lambda _f}} \right\}}^{ - 0.5}}} \right]} $ | (12) |
其中,zdM和z0M分别为Ma方法计算的零平面位移和粗糙度,α=4.43为拟合常数,λP=AP/AT为建筑顶面积系数(AP为建筑物顶面积,参见图 2),β=1.0为拖曳矫正参数(Kent et al., 2017),C1b=1.2为拖曳系数(Hall, 1996)。
Kanda等(2013)在Ma方法的基础上,考虑了最高建筑高度和建筑高度标准差两个几何参量的影响
| $ {\frac{{{z_{dK}}}}{{{z_{H{\kern 1pt} {\rm{max}}}}}} = {c_0}{X^2} + \left( {{a_0}\lambda _p^{{b_0}} - {c_0}} \right)X,X = \frac{{{\sigma _H} + \overline {{z_H}} }}{{{z_{H{\kern 1pt} {\rm{max}}}}}}} $ | (13) |
| $ {\frac{{{z_{0K}}}}{{{z_{0M}}}} = {b_1}{Y^2} + {c_1}Y + {a_1},Y = \frac{{{\lambda _p}{\sigma _H}}}{{{z_H}}},0 \le Y} $ | (14) |
其中,zdK和z0K分别为Ka方法计算的零平面位移和粗糙度,zHmax为最高建筑高度,带下标的a、b和c为回归常数(其中,方案一为:a0=1.29, b0=0.36, c0=-0.17, a1=0.71, b1= 20.21, c1=-0.77;方案二为:a0=0.86, b0=0.28, c0=-0.18, a1=0.93, b1=8.93, c1=4.68),σH为建筑高度标准差,z0M为Ma方法计算的动力学粗糙度(式(12))。
2.3 对比检验方法本文通过计算均方根误差(Root Mean Squared Error,RMSE)进行形态学、动力学方法结果对比
| $ RMSE = {\left[ {\frac{1}{N}\sum\limits_{i = 1}^N {{{({x_i} - {x_0})}^2}} } \right]^{\frac{1}{2}}} $ | (15) |
其中,xi、x0分别为形态学、动力学方法计算结果,N为计算样本容量。
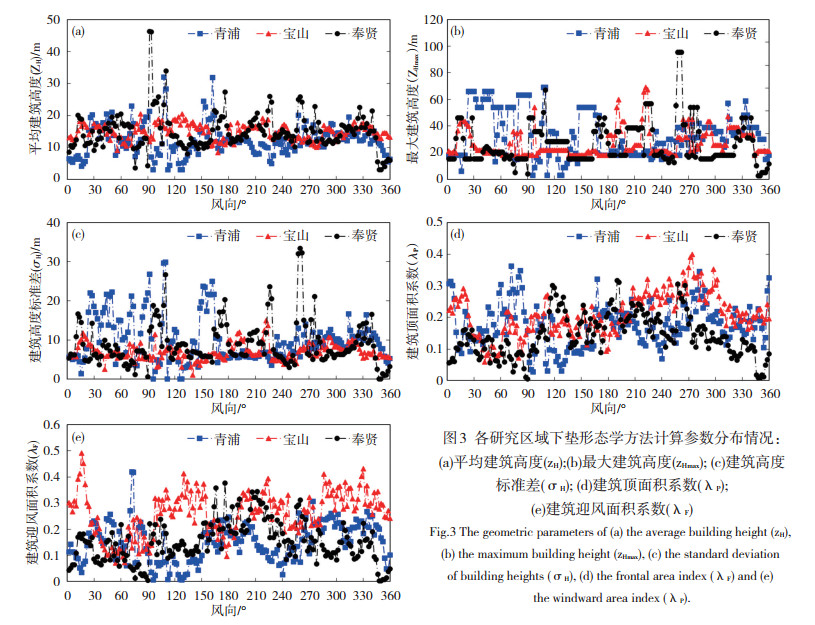
3 结果分析 3.1 形态学参数分布情况基于国家地理信息公共服务平台数据统计得到的三个研究区域粗糙元几何特征参数随风向的分布如图 3所示,平均建筑高度(下文简称zH,单位:m)、最大建筑高度(下文简称zHmax,单位:m)、建筑高度标准差(下文简称σH,单位:m)、建筑迎风面积系数(下文简称λF)和筑顶面积系数(下文简称λP)随风向变化明显,与建筑高度、密度等分布有较好的对应。其中,奉贤、青浦和宝山三个研究区域zH的范围分别为3.1~49.4、3.0~ 39.9和7.3~22.2,σH的范围分别为0.0~38.2、0.0~ 32.8和0.0~15.8,三个研究区域不同方向上建筑高度差异明显,为典型的城市下垫面特征;奉贤和青浦研究区域为商住混合区,建筑高度差异和分布密度差异更大,宝山研究区域为宝钢集团小区密集区域即居民住宅区,建筑高度差异和分布密度差异相对较小。后续章节将针对形态学计算方法在不同类型研究区域的应用效果进行对比和讨论。
|
图 3 各研究区域下垫形态学方法计算参数分布情况:(a)平均建筑高度(zH); (b)最大建筑高度(zHmax); (c)建筑高度标准差(σH); (d)建筑顶面积系数(λP); (e)建筑迎风面积系数(λF) Fig. 3 The geometric parameters of (a) the average building height (zH), (b) the maximum building height (zHmax), (c) the standard deviation of building heights (σH), (d) the frontal area index (λF) and (e) the windward area index (λP) |
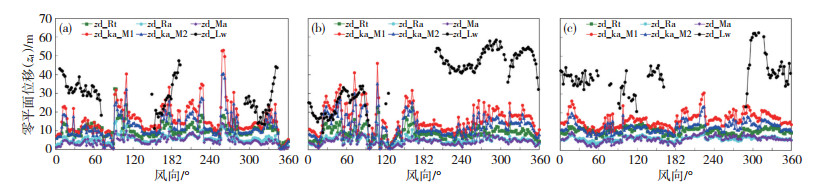
动力学和形态学方法计算的各研究区域零平面位移zd分布情况如图 4所示,其中,Lw方法结果在部分风向上的空缺为该风向有效数据不足(下文同)。在本文的三个研究区域中,不同方法zd计算结果差异明显:形态学方法分别在2.0~34.6 m (Rt)、0.2~15.1 m (Ra)、0~17.3 m (Ma)、0.5~54.5 m (Ka参数方案一)、0.5~41.0 m (Ka参数方案二),而动力学方法(Lw)结果范围为9.1~62.5 m,形态学方法结果小于动力学方法,这一结果与早前徐家汇研究区域的计算结果类似(唐玉琪等,2016)。其中,Lw方法计算结果平均为Ka和Rt方法的3~4倍,Ra和Ma方法的7~8倍,且随风向分布上差别明显;在四种形态学方法中,Ra与Ma方法计算结果的数值和分布趋势较为相似,Rt方法结果数值居中,而Ka方法最大,分布趋势与前三种方法也存在较明显差异。
|
图 4 基于多种计算方法的奉贤(a)、青浦(b)、宝山(c)零平面位移分布情况 Fig. 4 Zero-plane displacement (zd) distributions at (a) FX site, (b) QP site and (c) BS site based on different methods |
为探讨形态学方法结果的合理性,本文将多种方法计算的逐一与研究区域下垫面建筑高度等形态学参数进行对比,并结合卫星地图(图 1)进行分析验证。以奉贤为例,Lw和Ka方法的zd在13附近出现显著高值,而对应方向上Rt、Ra和Ma方法变化幅度较小。从卫星地图(图 1)上看,奉贤东北方向(0°—90°)主要为6~8层的住宅小区、3层别墅区,整体建筑高度在20 m内;但在15°附近,河流(浦南运河)、开阔平地(包括自然草地和奉贤区排水管理所区域)和公路(沪金高速)交汇,占据扇形分析区域过半比例。结合图 3a所示,该方向上的平均建筑高度zH虽变化不大(13°附近在zH=15.1 m,25°附近zH=12.2 m),但在13°附近建筑高度标准差σH和最高建筑高度zHmax (σH=13.6 m,zHmax=54.0 m)分别为临近区域(25°附近σH=5.2 m,zHmax=17.8 m)的四倍和三倍。其他相似区域(即zH变化不大,σH、zHmax出现高值)如奉贤(图 4a) 322°和340°、青浦(图 4b)的260°和313°,宝山(图 4c)的98 °和120 °,zH数值类似(10~20 m)、σH和zHmax分别为1.7~3倍关系的条件下,Ka方法的zd为1.4~2倍关系。而相反情况下,即σH、zHmax变化不大时,则五种形态学方法zH变化趋势相近。因此,建筑高度标准差σH和最高建筑高度zHmax的引入,使Ka方法对下垫面粗糙元高度的非均匀分布较其他形态学方法更为敏感,所以更适合城市复杂、非均匀下垫面的zd估算。
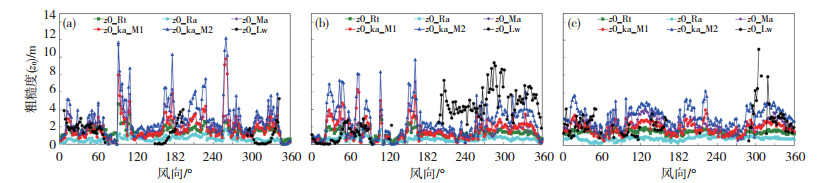
3.3 粗糙度分布情况不同方法得到的动力学粗糙度z0分布情况如图 5所示。首先除青浦(图 5b)外,Lw方法平均为Ma、Ka方法的0.6~1.3倍,Rt方法的1.0~1.8倍,Ra方法的3.3~3.8倍;与zd结果相比,形态学方法与动力学方法z0的差异较小,但随风向的分布趋势上仍存在明显不同。其次,在四种形态学方法中,数值上Ra < Rt < Ma≈ Ka_M1 < Ka_M2,与zd的结果明显不同之处在于,Ma方法的z0更接近于Ka方法,同时采用了不同参数方案的Ka方法也存在明显差异,并且方案二大于方案一,与zd的情况正好相反;趋势上,Rt和Ra方法结果较相近,Ka和Ma方法结果的变化趋势较相近。
|
图 5 基于多种计算方法的粗糙度分布情况: (a)奉贤,(b)青浦,(c)宝山 Fig. 5 Roughness length distributions at (a) FX site, (b) QP site and (c) BS site based on different methods |
与上节相类似,为探讨形态学方法计算结果的合理性,在zH基本一致、zHmax和σH变化较大的区域(如奉贤13°/25°、322°/340°,青浦260°/313°和宝山98°/ 120°方向),对不同形态学方法进行对比。结果表明,在zH数值类似(10~20 m)、σH和zHmax为分别1.7~3倍关系的四组方向上,Ka方法计算结果变化幅度最大,z0为1.4~3倍关系。与zd有所不同的是,Ma、Rt方法的z0分布与Ka方法更接近,只有Ra方法的整体变化幅度较小,说明形态学方法z0计算时敏感参数比zd更多。
4 形态学方法适用性分析 4.1 平均建筑高度、最大建筑高度和建筑高度标准差的敏感性基于上节空气动力学参数计算结果的初步分析,本节就各种形态学方法对不同计算参数的敏感度展开进一步研究。首先分析各形态学计算方法结果与计算参数zH、zHmax和σH的相关关系(R2),分析结果如表 2 (加粗数字为R2 ≥ 0.5,“-”为该计算方法未使用此计算参数)所示。形态学方法与计算参数的R2在不同研究区域存在一定差异,但总体上Ka方法计算结果与上述三个参数相关性均较高,即对建筑高度及其分布更为敏感。其中Ka方法的zd与zHmax、σH的R2大于zH,这与3.2节中Ka方法计算的zd对下垫面粗糙元高度非均匀分布更为敏感相一致;而z0则相反,即与zH的R2大于zHmax、σH,这与3.3节中z0对粗糙元高度非均匀性敏感度下降相一致。
|
|
表 2 形态学方法计算结果与平均建筑高度、最大建筑高度和建筑高度标准差相关关系(R2)分析 Table 2 Correlation coefficients between morphometric method results and zH, zHmax and σH |
此外Ma方法的z0与Ka类似,与zH的相关关系更显著,而zd则与zH相关关系均较差,这也解释了3.3节中Ma方法的z0与Ka方法分布趋势更接近的原因。而Ra则与Ma正好相反,zd与zH的相关关系较显著。结合上节的分析,Rt方法作为最简单估算方法(计算中只涉及zH一个参数),其在本文三个研究区域的计算结果与Ma、Ra方法差异不大,这一结论与Kent等(2017)的研究结果类似,因此在研究区域参数和观测均缺乏时,Rt方法为进行动力学参数估算的较好选择。
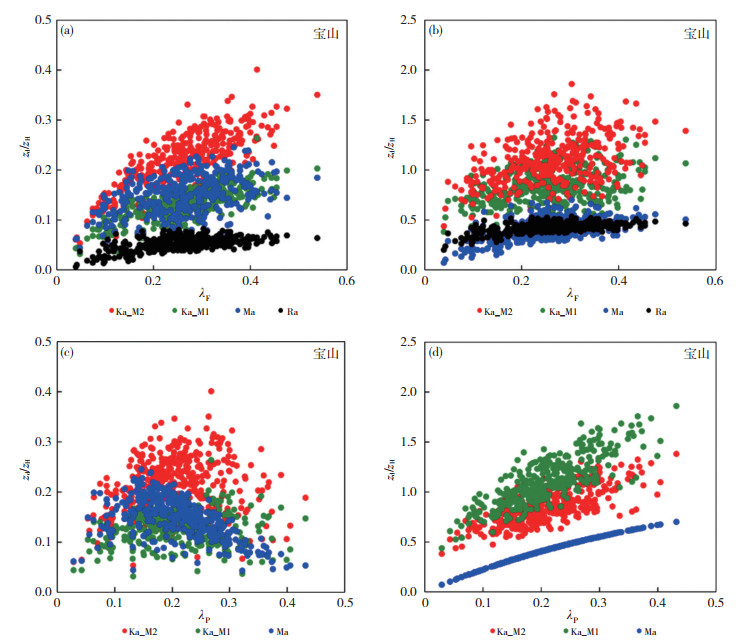
4.2 迎风面积系数和顶面积系数的敏感性除了上述三个计算参数,Ra、Ma和Ka方法还涉及建筑迎风面积系数(λF)和顶面积系数(λP)(参见表 1,其中Ra的计算只涉及λF),前者体现迎风方向粗糙元几何形态特征,后者表述粗糙元的排列密度。动力学参数与这两个系数的关系如图 6所示,首先,zd/zH随λF和λP的增加而增大。其中当λF > 0.1时,zd/zH增幅变缓,Ra和Ma方法最为明显;zd/zH随λP的正相关关系更显著,且没有明显拐点。其次,z0/zH与λF成正相关关系,随λP的增加呈现先增大后减小的抛物线变化,极大值出现在λP=0.15~0.25区间内。上述结果表明,Ka方法z0/zH与zd/zH与λF正相关,而Ra和Ma在λF < 0.1时与λF成正相关,当λF > 0.1时,Ra和Ma的标准化动力学参数几乎不在随λF变化,对λF敏感度下降。Ma和Ka方法的zd/zH与λP成正相关,相关性比λF更显著,说明这两种方法的zd对建筑密度变化更敏感度;而Ma和Ka方法z0/zH随λP成抛物线变化,说明在λP超过一定范围(0.15~0.25)时,z0随建筑密度的增大而减小。
|
图 6 归一化动力学参数(即zd/zH和z0/zH)与建筑迎风面积系数、建筑顶面积系数的关系 Fig. 6 Relationship between the frontal area index (λF), the plan area index (λP) and aerodynamic parameters normalized by average building height (zH) |
如图 7所示,本文三个研究区域λF70%以上大于0.1,λP则70%以上小于0.25,即多层/高层楼房区域,为Ka方法敏感区间,因此在本文研究区域下垫面特征条件下,更适合使用Ka方法进行动力学参数估算。
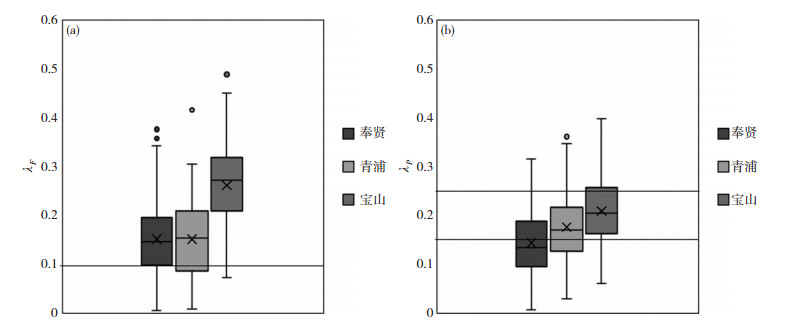
|
图 7 研究区域建筑迎风面积系数(λF,a)、建筑顶面积系数(λP, b)的分布范围 Fig. 7 (a) Frontal area index (λF), and (b plan area index (λP) range of study areas |
在本文三个研究区域上,形态学方法与动力学方法计算的空气动力学参数在数值和分布趋势上都有差异,这与早前徐家汇研究区域(唐玉琪等,2016)、国外相关研究(Grimmond et al., 1998;Kent et al., 2017)结果类似,即没有一种形态学方法结果与动力学方法一致。下面结合研究区域下垫面粗糙元分布及土地类型、计算公式和影响因素等方面进行可能原因的分析。
首先,根据Lw方法计算公式(式(1)-式(4)),其零平面位移z0L是观测高度zsi和风速Ui的函数;观测高度zsi的高低、Ui的大小影响各风向观测源(也称“足迹”)的大小,即各风向的观测源是zsi和Ui的函数,并非常数。如奉贤铁塔北面(图 1a)有东-西向的浦南运河和南-北向的沪金高速,河道两岸和高速两侧有较大面积绿地,因此该区域建筑高度为10 m左右(图 3a),建筑密度也较小(图 3d、e),因此形态学方法计算的zd也较小;而由于下垫面较开阔,铁塔测风仪器在此方向上数据源区大小相应增加,对应方向(约330°)半径1 km边界附近有10~18层的高层小区,动力学方法计算的zd受此影响出现高值,而形态学方法计算参数范围限制在铁塔为中心半径、1 km区域内,因此未考虑这片高层建筑的影响;此外,南-北向贯穿奉贤研究区域东侧的沪金高速,其往来车流也对相应区域的气流产生额外扰动,进而影响动力学方法计算结果,使之与形态学计算结果的分布趋势产生差异。其次,局地尺度的风速还会受下垫面热力性质差异(在建筑林立的城市区域尤其明显)影响。如青浦铁塔西面为较密集的居民区(图 1b),建筑高度15 m左右(图 3a),建筑密度较高(图 3d、e),形态学方法计算得到的zd也较大(图 4b),动力学方法结果分布趋势与之类似但数值更大,即可能与居民区低层人为热源更明显、气流扰动更大相关(Kotthaus et al., 2012;Kent et al., 2017);作为居民区典型的宝山研究区域,也出现显著的动力学方法zd计算结果普遍大于形态学方法的情况(图 3c)。相比之下,形态学方法计算参数为固定区域(铁塔为中心半径、1 km区域)内粗糙元几何数据,不受热力性质差异、局地环境气流扰动等气象因素影响,计算结果更具有确定性。动力学方法z0的计算以zd为计算参数,因此,两类方法计算的z0也存在数值或分布趋势上的差异。
由于动力学方法受到观测仪器布设条件限制(必须有铁塔和风温观测数据),具备大气稳定度条件(Lw方法只能在近中性条件下进行计算),同时受局地热力性质差异(建筑类型导致的人为热差异)和局地扰动(如高速公路汽车尾流)等气象因素的影响,可用于计算分析的区域不多,计算区域面积(数据源区)、风向区间(数据样本)有限,同时受气象因素扰动其结果具有不稳定性。因此,形态学计算方法的应用成为新的趋势。形态学方法经过不断发展,目前存在多种计算方式,包含不同的粗糙元几何参数。以传统动力学方法(Lw)计算结果为参考值,分别计算三个研究区域四种形态学方法(Rt、Ra、Ma、Ka)与其的RMSE(式(15)),分析最适合上海区域的形态学计算方法,结果如表 3所示。动力学方法和形态学方法计算结果存在较显著差异,其中,以Ka方法参数方案一(Ka_M1)的结果与Lw方法最接近,RMSE各站均值分别为17.39 m和1.68 m。从各研究区域结果看,奉贤动力学方法与形态学方法结果最为相似,而青浦差异最大。对比三个研究区域下垫面粗糙元特征(图 3b ),青浦各风向区间建筑高度标准差平均值(9.950 m)和离散程度(6.161 m)均最大,这一特征从卫星地图(图 1c)中该区域内包括老式6~7层住宅小区、新建高层住宅区、学校、公园、湖泊等的情况也得以印证。说明在建筑高度差异越大的区域,形态学方法(Rt、Ra、Ma、Ka)与动力学方法(Lw)的差异也越大。
|
|
表 3 形态学方法与动力学方法计算结果均方根误差(RMSE)分析 Table 3 The root-mean-squared error (RMSE) analysis between results of morphometric method and aerodynamic method |
此外,值得关注的是除青浦外,Rt方法的RMSE接近或略小于Ma方法,再次说明在气象观测资料、形态学数据较少,Rt方法可作为空气动力学参数估算的有效方法。
5 结论及讨论(1) 在本文研究区域内,形态学方法(Rt、Ra、Ma和Ka)与动力学方法(Lw)计算的动力学参数在数值和分布趋势上都有差异。其中,形态学方法的零平面位移(zd)显著小于动力学方法,四种形态学方法中Ka方法结果最大,分布趋势与动力学方法也最为接近;动力学与形态学方法的粗糙度(z0)的差异相对较小,四种形态学方法中Ma和Ka与动力学方法结果较为接近。
(2) 适用性分析中,分别对四种形态学方法对计算参数的敏感性进行了对比。Ka方法计算结果与zHmax、σH和zH的相关性均较高,其中zd与zHmax、σH的相关系数大于zH,即Ka方法zd对建筑高度的非均匀分布更敏感;z0则相反,与zH的相关关系更显著。Ma方法的z0与Ka方法相似。在面积系数λF和λP的敏感性分析中,Ka方法随λF和λP变化最显著,即对建筑排列方式最敏感。首先,Ka的z0/zH与zd/zH与λF正相关,而Ra和Ma在λF > 0.1对λF敏感度下降;Ma和Ka方法的zd/zH与λP也成正相关,而z0/zH随λP先呈正相关,在λP超过一定范围呈负相关。
(3) 本文研究区域下垫面粗糙元几何特征(七成以上区间λF > 0.1,λP < 0.25)与Ka方法敏感区间相一致,并通过与动力学方法(Lw)结果的对比,认为Ka方法的方案一(Ka_M1)最适用于以本文研究区域为代表的、上海典型城市下垫面的动力学参数估算。同时,在观测资料、形态学数据较少的情况下,Rt方法可作替代方案进行计算和分析。
上海共有9座铁塔梯度观测站,均有较长时间序列的气象观测资料,然而受下垫面建筑、植被等粗糙元几何数据缺乏影响,本文只对其中三站进行了计算和分析。此外,下垫面动力学参数作为地气相互作用的重要参数之一,在数值模式参数化中具有重要意义,今后将尝试将计算所得动力学参数数据集应用到数值模式中,分析研究其对局地尺度天气系统预报能力的影响。
高志球, 卞林根, 逯昌贵, 等. 2002. 下垫面空气动力学参数的估算[J]. 应用气象学报, 3(特刊): 26-33. |
胡文超, 张文煜, 张宇, 等. 2010. 河西走廊下垫面粗糙度实测值与模拟值的差异性分析[J]. 高原气象, 29(1): 51-55. |
鞠英芹. 2012.不同下垫面类型动力学粗糙度与热力学粗糙度的研究[D].南京: 南京信息工程大学 http://cdmd.cnki.com.cn/Article/CDMD-10300-1012369103.htm
|
琚陈相, 李淑娟, 于晓晶, 等. 2014. GRAPES模式中不同陆面方案对新疆一次强降水事件的模拟[J]. 沙漠与绿洲气象, 8(6): 16-22. DOI:10.3969/j.issn.1002-0799.2014.06.003 |
刘小平, 董治宝. 2003. 空气动力学粗糙度的物理与实践意义[J]. 中国沙漠, 26(4): 3-12. |
邱传涛, 李丁华. 1997. 平均风向的计算方法及其比较[J]. 高原气象, 16(1): 94-98. DOI:10.3321/j.issn:1000-0534.1997.01.012 |
唐玉琪, 谈建国, Grimmond C S B, 等. 2016. 典型特大城市下垫面空气动力学特征参数的计算与分析研究[J]. 热带气象学报, 32(4): 503-514. |
熊仕焱, 曾新民, 刘金波, 等. 2010. 陆面参数随机扰动对一次暴雨过程模拟的影响分析[J]. 暴雨灾害, 29(2): 117-121. DOI:10.3969/j.issn.1004-9045.2010.02.003 |
张宏升, 陈家宜. 1997. 非单一水平均匀下垫面空气动力学参数的确定[J]. 应用气象学报, 8(3): 310-315. |
张文煜, 张宇, 陆晓静, 等. 2009. 黄土高原半干旱非均一下垫面粗糙度分析[J]. 高原气象, 28(4): 763-768. |
张文煜, 刘欣, 张宇, 等. 2011. 河西地区两种计算粗糙度方法的差异性[J]. 兰州大学学报(自然科学版), 47(3): 40-43. |
赵鸣. 2008. 边界层和陆面过程对中国暴雨影响研究的进展[J]. 暴雨灾害, 2(2): 186-190. DOI:10.3969/j.issn.1004-9045.2008.02.016 |
周艳莲, 孙晓敏, 朱治林, 等. 2007. 几种典型地表粗糙度计算方法的比较研究[J]. 地理研究, 26(5): 887-896. DOI:10.3321/j.issn:1000-0585.2007.05.004 |
Grimmond C S B, King T S, Roth M, et al. 1998. Aerodynamic roughness of urban areas derived from wind observations[J]. Boundary-Layer Meteor, 89: 1-24. DOI:10.1023/A:1001525622213 |
Grimmond C S B, Oke T R. 1999. Aerodynamic properties of urban derived from analysis of surface form[J]. J Appl Meteor, 38: 1262-1292. DOI:10.1175/1520-0450(1999)038<1262:APOUAD>2.0.CO;2 |
Hall D, Macdonald J R, Walker S, et al. 1996. Measurements of dispersion within simulated urban arrays-a small scale wind tunnel study[J]. BRE Client Report, CR178/96
|
Kanda M, Inagaki A, Miyamoto T, et al. 2013. A New Aerodynamic Parametrization for Real Urban Surfaces[J]. Boundary-Layer Meteor, 148: 357-377. DOI:10.1007/s10546-013-9818-x |
Kent C W, Grimmond C S B, Barlow J, et al. 2017. Evaluation of Urban Local-Scale Aerodynamic Parameters:Implications for the Vertical Profile of Wind Speed and for Source Areas[J]. Boundary-Layer Meteor, 164(2): 183-213. DOI:10.1007/s10546-017-0248-z |
Kotthaus S, Grimmond C S B. 2012. Identification of micro-scale anthropogenic CO2, heat and moisture sources-processing eddy covariance fluxes for a dense urban environment[J]. Atmos Environ, 57: 301-316. DOI:10.1016/j.atmosenv.2012.04.024 |
Lettau H. 1957. Compilation of Richardson numbers, classification of profiles and determination of roughness parameters.In: Lettau HH, Davidson B (eds) Exploring the atmosphere's 1st Mile, Pergamon Press, London, 376 pp
|
Macdonald R W, Griffiths R F, Hall D J. 1998. An improved method for the estimation of surface roughness of obstacle arrays[J]. Atmos Environ, 32: 1857-1864. |
Martano P. 2000. Estimation of surface roughness length and displacement height from single-level sonic anemometer data[J]. J Appl Meteorol, 39: 708-715. DOI:10.1175/1520-0450(2000)039<0708:EOSRLA>2.0.CO;2 |
Mohammad A F, Zaki S A, Ali MSM, et al. 2015. Large eddy simulation of wind pressure distribution on heterogeneous buildings in idealized urban models[J]. Energy Proc, 78: 3055-3060. DOI:10.1016/j.egypro.2015.11.725 |
Raupach M R. 1994. Simplified Expressions for Vegetation Roughness Length and Zero-Plane Displacement as Functions of Canopy Height and Area Index[J]. Boundary-Layer Meteor, 71: 211-216. DOI:10.1007/BF00709229 |
World Meteorological Organization. 2006. Guide to Meteorological Instruments and Methods of Observation (The Seventh Edition)[R] C5-12
|
 2020, Vol. 39
2020, Vol. 39 