引言

降雪是我国北方地区冬季常见的降水形态，我国仅东北地区平均每年就有七到八场降雪过程发生，雪灾也是我国北方地区重要的自然灾害之一，以2007年3月上旬东北三省出现的暴雪和特大暴雪天气为例，该过程中，仅辽宁省就有6个城市雪深超过30 cm，其中3月5日凌晨沈阳市积雪深度达36 cm，创该地区百年气象记录之最，受灾地区较长时间内海陆空交通全面瘫痪，数万人被困，房屋倒塌1 100多间、中小学停课、工厂停产、城市停水停电停气，因灾造成的直接经济损失达约百亿元(韩秀君等，2016)，给人民的生命财产带来了严重的威胁，给社会生产生活造成了极大的不便。

降雪深度预报是北方地区冬季气象服务的重点，本文中降雪深度是指新增部分积雪的深度，区别于积雪深度之处在于后者包含了该次降雪发生之前的雪深，在该次降雪发生之前雪深为0的情况下，降雪深度等同于积雪深度。目前，我国北方地区在尚未有理想的降雪深度客观预报产品的情况下，基本仍使用传统的降雪深度预报方法即降雪深度等于降水量与新降雪密度之比，这里的新降雪密度指单位体积降雪的质量，区别于雪密度之处在于后者指单位体积新增积雪(新雪)和该次降雪发生前地面已有积雪(旧雪)的质量，在该次降雪发生前地面无旧雪的情况下，等同于新降雪密度。降水量预报和新降雪密度估算的精度共同决定着降雪深度预报的准确性，当前高分辨率数值天气预报模式迅速发展，定量降水预报水平逐步提升(Roads and Maisel, 1991；Olson et al., 1995；Mcbride and Yau, 2000；Damrath et al., 2000；王雨等，2006)，而新降雪密度的变化范围较大, 约为10~350 kg·m^-3 (Roebber et al., 2003；Currie，1947；Lachapelle，1962；Power et al., 1964；Super and Holroyd, 1997)，即同样的降水量造成的降雪深度可以相差几十倍，因此，新降雪密度估算成为降雪深度预报的关键技术。

关于新降雪密度的估算，国内外相关领域的学者已经进行了大量的研究，并建立了较为实用的计算方法：(1)新降雪密度取为常数。如降雪含水比(即新降雪深度与融化后等量液体深度的比值)10:1法，即新降雪密度为常数0.1 g·cm^-3(Alcott and Steenburgh, 2010；崔锦等，2017)，Loth(1993)建立的一个多层雪盖模式中，新降雪密度当气温大于-15 ℃时取为0.08 g·cm^-3，当气温小于-15 ℃时，取为0.05 g·cm^-3，Dai与Zeng (1997)在发展的中国科学院大气物理研究所陆面模式IAP94 (Institute of Atmosphere Physics)中，新降雪密度估算引用了该方法。(2)建立基于地面气象要素的新降雪密度估算公式。例如：Gottlieb (1980)建立的新降雪密度估算方法中，新降雪密度在2 m温度小于-15 ℃时被设为常量，在2 m温度大于-15 ℃时，被设为2 m温度的1.5次方函数(Gottlieb，1980；Anderson, 1976, 2006)，该方法被广泛采纳和应用，如NCEP发展的Noah陆面模式、Dawson等(2017)开发的SNODEN雪密度参数化方法中均采用该估算方法；Hedstrom and Pomeray(1998)建立的雪密度估算方法将新降雪密度设为以自然常数e为底的气温的指数函数，Yang等(2011)发展的Noah-MP (MultiParameterization options)陆面模式采用了该方法，CROCUS雪盖模式新降雪密度估算考虑了固态水的融点温度和地面风速(Vionnet et al., 2012)；SNOWPACK雪盖模式新降雪密度估算综合考虑了气温以及地面温、湿、风等多种地面气象要素(Lehning et al., 2002)；Yamaguchi等(2004)对SNOWPACK雪盖模式进行本地化应用时，对新降雪密度的估算方法进行了简化，只保留了气温和地面风速两个变量。(3)还有以温度垂直廓线为主要参考依据的新降雪密度诊断流程。Dubé (2003)基于魁北克地区的观测研究，建立了一种新降雪密度诊断预报流程，该流程依据温度垂直廓线分两种情况诊断雪粒子类型，进而确定新降雪密度，并将该方法用于数值天气预报模式。(4)基于数值天气模式中整体微物理方案诊断雪密度。Milbrandt等(2012)基于整体微物理方案，发展了由数值天气模式直接输出瞬时新降雪密度的方法，该新降雪密度的估算思路是由微物理过程中已知或计算得到的冰、霰粒子密度、各类粒子的粒径分布、下落末速度、混合比、降水粒子粒径质量关系，并假设雪粒子为球形，由固态、液态降水体积加权之和以及降水量计算得到新降雪密度。

本文将围绕新降雪密度估算这一核心内容，简略回顾新降雪密度估算中需要着重考虑的气象要素，详细介绍近几十年来，国内外围绕设为常数法、建立公式法、后处理诊断法、基于微物理过程法等几种被广泛应用的新降雪密度估算方法的主要研究成果，在此基础上，评述几种估算方法的特点、局限性以及它们之间的承接联系，并对未来新降雪密度估算的发展方向进行展望。

2 新降雪密度的主要影响要素

在提高新降雪密度估算精度需求的推动下，人们开始深入微物理过程从云顶到地面全程追踪雪粒子的生成、发展和着陆过程，研究雪粒子从云中生成到降落地面的各阶段影响新降雪密度的主要因素及其影响机制，研究表明，温度、风速、湿度、太阳辐射与降水量是几个主要的影响要素。

2.1 温度

研究表明，温度是决定雪粒子形状和密度，进而影响新降雪密度的首要气象要素。首先，云中温度是雪粒子生成形状与大小的主要影响因素，而形状与大小决定着雪粒子的密度。按照密度由大到小的顺序，雪粒子主要分为以下几类：盘状、针状、柱状、星状、枝状等(Magono and Nakamura, 1965，1966；Ryan et al., 1976；Fukuta and Takahashi, 1999)，它们也基本对应于由高到低的云中生成温度即：盘状0~-3 ℃、针状-3~ -6 ℃、柱状-6~-10 ℃、星状-10~-12 ℃、枝状-12~ -16 ℃。当温度从-16 ℃再度降低时，生成的雪粒子密度又开始增大，-16~-22 ℃主要生成星状雪粒子，低于-22 ℃主要生成柱状雪粒子，即-15 ℃左右是大粒径、低密度雪粒子的最佳生长条件(Dubé，2003；Pruppacher and Klett, 2012；Roads and Maisel, 1991)。

其次，云下温度改变雪粒子密度。雪粒子从云中降落到地面的过程中，由温度、湿度、风速条件诱发的升华、融化、冻结、吸积、破碎等过程对雪粒子的形状和大小进行修饰，从而改变雪粒子的密度。温度条件是融化、冻结过程发生与否的决定因素，温度大于0 ℃暖层的厚度、强度等决定融化的程度和融化后雪粒子的密度，冻结发生在上暖(温度 > 0 ℃)下冷(温度 < 0 ℃)层结结构的冷层中，冷暖层的相对厚度和强度决定着经过冻结层后雪粒子的类型和密度；在适宜的温度条件下(0~-10 ℃)也会发生雪粒子吸积过冷却水滴、出现结晶的现象，从而导致雪粒子密度增加等微物理过程，不同的雪粒子类型吸积后会发生密度变大或者变小的不同可能。

再次，地面温度影响新降雪密度。雪粒子一旦落到地面，会有各种过程影响新降雪密度。较高的地表温度会造成雪粒子的融化、变态，进而影响新降雪密度。

2.2 风速

风速对新降雪密度的影响也贯穿于雪粒子从云中生成到降落地面的整个过程中。云中气流的上升速度影响雪粒子的生长时间，较大上升速度是低密度降雪发生的重要动力条件，研究表明，配合较高的相对湿度(> 80%)和适宜的温度(15 ℃左右)，较强上升气流的持续托举能够让雪粒子在适宜的生长环境中较长时间停留，进而形成枝状或类似枝状的低密度雪片，而这些气象条件也成为低密度降雪发生的重要热力条件和具有指示意义的降雪预报指标。Dubé(2003)指出，垂直速度也是雪粒子主要生长层和次要生长层的主要划分依据，在满足相对湿度大于80%的条件下，主要生长层位于上升速度最大层、次要生长层位于主要生长层以下且上升速度小于0。云下大风是破碎过程发生的必要条件，大风过程使得雪粒子间相互撞击而破碎，雪粒子粒径变小进而使降落到地面的新降雪密度增加。地面风速影响雪密度的主要原因也在于风对于雪片的破碎作用，风速较大时(大于9 m·s^-1)可以使冰晶在地表移动，冰晶在移动过程中破裂，引起地表压实，新降雪密度增加(Roebber et al., 2003)。

2.3 湿度

湿度条件通过在云中影响雪粒子的大小、在云下影响升华过程而影响新降雪密度。如前所述，雪粒子主要生长层和次要生长层均需满足相对湿度大于80%，即湿度条件是雪粒子生长的必要条件之一，只有满足了湿度条件，水凝物才可能存在、降水过程才有可能发生。云中雪粒子周围空气的过饱和程度决定着雪粒子的增长速度，如果周围空气过饱和程度较高，则雪粒子增长较快、粒径较大，反之亦然。云下湿度条件是升华过程发生与否的决定因素，当雪粒子周围空气不饱和时，升华过程发生，固态雪粒子的一部分尤其是尖锐边角部分变为气态，使得雪粒子粒径减小、密度增加。

2.4 太阳辐射与降水量

Roebber等(2003)建立的集成人工神经网络法将新降雪密度诊断为重(0.11~1 g·cm^-3)、中(0.07~0.11 g·cm^-3)、轻(< 0.07 g·cm^-3)三类，其准确率达60.4%，较使用样本气候学法(准确率为41.7%)和10:1法(准确率为45%)有明显的提高。该方法中考虑了太阳辐射、中低层温湿及外部压缩(来自地面风速和降水量)等7个主要气象要素，且强调太阳辐射、温度和外部压缩是最为关键的影响因子。对于太阳辐射在确定雪密度中的重要性，Roebber等(2003)基于两组探空-地面数据进行了如下的试验：集合A由20对探空-地面数据组成，它们紧密匹配，由探空-地面数据对之间的欧几里得距离(指m维空间中两个点之间的真实距离)定义，每对数据中一个为秋季探测、另一个为春季探测，集合B由64对紧密匹配的探空-地面数据组成，每对数据中一个为秋季或春季探测，另一个是冬季探测。如果太阳辐射是确定新降雪密度的一个重要因素，那么A组应在匹配对之间产生比B组更相似的雪比(等同于新降雪密度的倒数)，结果表明，A组探空-地面数据对之间的雪比等级一致性为60%，而B组仅为42%，这证明了太阳辐射对于确定新降雪密度的重要性。太阳辐射与一年中的时间密切相关，该研究中用月度指数表示太阳辐射：7月份为-1、1月份为1，相邻月间隔为0.33，每两个与1(或7)月时间间隔相同的月份视为同样的月度指数。

考虑到地面压实过程，该人工神经网络法还采用了降水量作为输入，雪降落到地表后，会由重量造成压缩而增加新降雪密度，压缩的强度主要受降水量影响(Gray and Male, 1981)。

3 新降雪密度的主要估算方法

目前被广泛应用的新降雪密度估算方法有设为常数法、建立公式法、后处理诊断法和基于微物理过程法等四类。

3.1 设为常数法

新降雪密度在最初乃至现在经常被取为常数0.1 g·cm^-3，也称(降雪含水比，即新降雪深度与融化后等量液体深度的比值)10:1法，这个数值来源于十九世纪加拿大多伦多天文台前台长雷弗罗伊(Potter, 1965；Roebber et al., 2003)的一系列实验的结论，但这是一个平均值，代表着新降雪密度的平均状态(Judson and Doesken, 2000)。这一新降雪密度取值在降雪深度预报实践中被广泛应用，甚至现在的降雪深度预报仍基于该数值，只是在此基础上，根据实际天气情况作相应的调整。

Loth等(1993)雪盖模式中根据气温将新降雪密度分为两个等级，即当气温大于-15 ℃时，新降雪密度取0.08 g·cm^-3，当气温小于-15 ℃时，新降雪密度取0.05 g·cm^-3，详见式(1)

$ {\rho _{{\rm{sn}}{\kern 1pt} ow}} = \left\{ {\begin{array}{*{20}{l}} {0.08}&{({T_{air}} > - {{15}^\circ }C)}\\ {0.05}&{({T_{air}} < - {{15}^\circ }C)} \end{array}} \right. $

(1)

其中ρ_{sn ow}表示新降雪密度；T_air表示气温，下同

此外还有其他根据气温将新降雪密度分为多个等级的方法，如1996年美国国家气象局建立并使用的气温与新降雪密度间的对应关系，详见表 1(Dubé, 2003)。这些方法均是基于大量的观测事实得到的统计结果。

3.2 建立公式法

新降雪密度估算公式的建立均基于统计和相关，即类似于经验公式，因此，所建立的估算公式随着研究区域、数据来源、统计方法以及一些主观因素的变化而不同，其中产生了较大影响力并发挥了较大应用价值的估算公式有如下几个。

Gottlieb (1980)在其发展的雪盖和冰川盆地径流模式中建立的新降雪密度估算方法较为经典，该方法被应用于NCEP (National Center for Environmental Prediction)、OSU (Oregon State University)、Air Force、Hydrologic Research Lab等单位共同发展的(并应用于NCEP中尺度及全球模式中的)Noah陆面模式(Ek et al., 2003)以及Dawson等(2017)开发的雪密度参数化方法SNODEN中。Gottlieb方案中，新降雪密度在2 m温度小于-15 ℃时被设为常量，在2 m温度大于-15 ℃时，被设为2 m温度的1.5次方函数，详见(2)式

$ {\rho _{{\rm{sn}}{\kern 1pt} ow}} = \left\{ {\begin{array}{*{20}{l}} {0.05}&{({T_{2m}} < - {{15}^\circ }C)}\\ {0.05 + 0.0017 \times {{({T_{2m}} + 15)}^{1.5}}}&{({T_{2m}} > - {{15}^\circ }C)} \end{array}} \right. $

(2)

其中T_2m表示2 m温度，下同。

Hedstrom与Pomeroy(1998)在水文研究中根据Schmidt与Gluns(1991)和美国陆军工兵队1956年的数据建立了一个新降雪密度经验估算公式，Yang等(2011)发展的Noah-MP (MultiParameterization options)陆面模式采用了该新降雪密度估算方法，该方案中新降雪密度为以自然常数e为底的气温的指数函数，具体如(3)式所示

$ {\rho _{{\rm{sn}}{\kern 1pt} ow}} = 67.92 + 51.25 \times {\rm{exp}} ({T_{air}}/2.59) $

(3)

Crocus雪盖模式(Vionnet et al., 2012)中，新降雪密度除气温外，考虑了地面风速和固态水的融点温度，详见(4)式

$ {\rho _{{\rm{sn}}{\kern 1pt} ow}} = 109 + 6 \times ({T_{air}} - {T_{fus}}) + 26 \times {U^{1/2}} $

(4)

其中T _fus为固态水的融点温度，U代表地面风速，下同。

SNOWPACK雪盖模式中(Lehning et al., 2002)的新降雪密度估算方案除气温外，还考虑了地面温、湿、风等诸多地面气象要素，是目前为止考虑气象要素最多的雪密度估算方案之一，详见(5)式

$ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rho _{{\rm{ sn}}{\kern 1pt} ow{\rm{ }}}} = 70 + 6.5 \times {T_{air}} + 7.5 \times TSS + 0.26 \times RH + 13 \times \\ U - 4.5 \times {T_{air}} \times TSS - 0.65 \times {T_{air}} \times U - 0.17 \times RH \times U + \\ 0.06 \times {T_{air}} \times TSS \times RH \end{array} $

(5)

其中TSS为地面温度，RH地面相对湿度，U地面风速。

Yamaguchi等(2004)将SNOWPACK雪盖模式本地化时，对新降雪密度估算方法进行了如(6)式的修改

$ {\rho _{{\rm{ sn}}{\kern 1pt} ow{\rm{ }}}} = 3.6 \times U - 0.2 \times {T_{air}} + 62 $

(6)

将由基于多个气象要素估算新降雪密度的方法简化回仅由气温和地面风速进行估算。

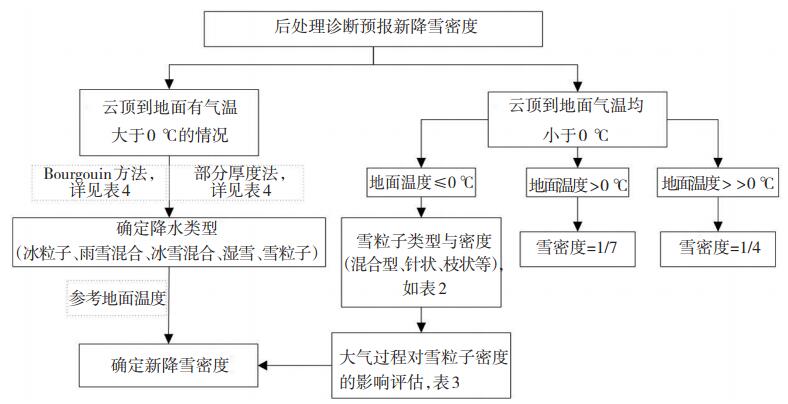
3.3 后处理诊断法

Dubé(2003)基于魁北克地区的观测研究，建立了一种基于数值天气预报模式预报场的新降雪密度诊断流程，该方法依据温度垂直廓线分两种情况对新降雪密度进行诊断，如图 1所示：第一，当云顶到地面的气温均小于0 ℃时，新降雪密度根据地面温度分成三类，若地面温度远大于0 ℃则新降雪密度等于0.25 g·cm^-3，若地面温度大于0 ℃则新降雪密度约等于0.14 g·cm^-3，若地面温度小于等于0 ℃则新降雪密度由雪粒子类型及密度决定，雪粒子的类型主要由其主要生长层和次要生长层中的温度环境决定(表 2)，并根据吸积、低层大风、升华、聚集等天气过程的发生与否对雪粒子密度进行调整(表 3)。第二，当云顶到地面的温度有大于0 ℃的情况时，新降雪密度由降水类型(冰粒子、雨雪混合、冰雪混合、湿雪、雪粒子)和地面温度决定，降水类型的诊断基本均依据温度垂直廓线，可采用的诊断方法有Bourgouin方法(Peter，2005)、部分厚度法(Dubé(2003))等，两种诊断方法的原理类似，即判断环境中是否有足够的能量来融化或者冻结水凝物粒子，Bourgouin方法(Bourgouin，2000)或基于温熵图或基于Iribarne与Godson(1981)的经验公式计算某处温度廓线正(温度大于0 ℃)/负(温度小于0 ℃)区能量即PE(正能量)/NE(负能量)，根据空中和地面PE和NE的数值匹配判断降水类型，该能量计算经验公式如(7)式所示

$ {c_p}|{\rm{ }}Area{\rm{ }}| = {c_p}\oint T d\ln \theta = {c_p}{\bar T_l}\ln \left({\frac{{{\theta _{top}}}}{{{\theta _{bottom}}}}} \right) $

(7)

其中c _p为一定气压条件下的比热容，单位：J·(kg·℃)^-1，T为绝对温度(单位：K)，θ为位温(单位：K)，θ_top为层顶位温、θ_bottom为层底位温，T_l为由层顶到层底的平均温度。部分厚度法基于850~700 hPa和1000~850 hPa的厚度组合判断降水类型(表 4)。

3.4 基于微物理过程法

随着计算机技术的飞速发展，复杂的云微物理方案可以在高分辨率天气模式中使用，整体微物理方案BMS (Bulk Microphysics Schemes)在数值天气预报模式的研究和业务应用中发挥着越来越重要的作用，BMS的主要特征为云雨冰雪霰雹等各类粒子的粒径分布均由一个三参数的Gamma函数近似描述。BMS通过水相态转换过程中的潜热释放和浮力变化影响模式动力过程，通过水凝物表面场的产生与辐射过程相互作用，且负责降水相态、类型、量级的预报(Milbrandt and Jacob, 2009)。

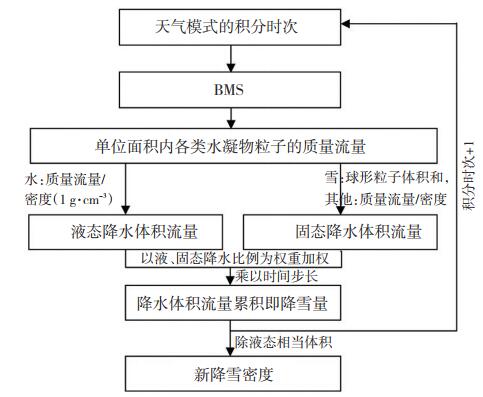
Milbrandt等(2012)基于整体微物理方案Milbrandt 2-mom(Milbrandt et al., 2005a, 2005b, 2009, 2012, 简称MY2方案)发展了一种使用微物理过程中的信息直接预报某时刻新降雪密度(或瞬时雪密度)的方法，此微物理方案的主要特征为仅诊断云雨冰雪霰雹等每类降水粒子尺寸分布的总数浓度和质量混合比，该方案中表示水凝物尺寸分布的Gamma函数为N _x(D) = N_{0 x} D^μ_xe^{-λ_x D}其中N _x(D)为总数浓度，即单位体积内直径为D的x类粒子的数量，N_{0 x}、λ _x、μ_x分别是截距、斜率和形状参数，μ_x为固定值，当x代表冰、雪、霰、雨、雹时μ_x = 0，当x代表云时，μ_x = 3，D为粒子直径。该新降雪密度的预报思路(如图 2所示)为：

第一步，计算单位面积内各类沉降的水凝物粒子的质量流量

$ {F_{{m_ - }x}} = \int_0^\infty {{m_x}} (D){V_x}(D){N_x}(D)dD $

(8)

其中D表示单个粒子的粒径，m _x(D)、V_x(D)、N_x(D)分别表示不同类型、不同粒径粒子的质量、下落末速度、粒径分布，下标x表示不同的水凝物类型，x = i, s, g, r分别代表冰、雪、霰、雨，下同。m_x(D)分别由各类粒子的粒径质量关系计算得到。

第二步，计算单位面积内液态、固态降水体积流量。雨、冰、霰体积由质量密度之比计算，液态水密度为1 g·cm^-3、冰和霰粒子密度设为固定值；方案中假设雪粒子为球形，降雪体积由球形粒子体积相加得到；再分别统计液态和固态降水体积流量。

$ {F_{v\_liq}} = \frac{1}{{{\rho _L}}}{F_{m\_liq}} $

(9)

$ F_{{v_{{\rm{sn}}{\kern 1pt} ow}}}^\prime = \frac{{{F_{m\_i}}}}{{{\rho _i}}} + \frac{{{F_{m\_g}}}}{{{\rho _g}}} + \int_0^\infty {\frac{\pi }{6}} {D^3}{V_s}(D){N_s}(D)dD $

(10)

F_{v _liq}、F_{vsn ow}^’分别为液态和固态降水体积流量，ρ_L、ρ_i、ρ_g分别为液态水、冰、霰密度

第三步，计算单位面积内液态、固态降水加权体积流量。

$ {f_{liq}} = \frac{{{q_r}}}{{{q_{total}}}} = \frac{{{q_r}}}{{{q_r} + ({q_i} + {q_g} + {q_s})}} $

(11)

f_liq液态降水所占比例，下标liq表示液态水，q表示混合比，下标total表示冰雪霰雨之和。

$ {{F}_{v\_\text{sn}ow}}=\left\{ \begin{array}{*{35}{l}} (1-{{f}_{liq}})F_{{{v}_{\text{sn}ow}}}^{^\prime}+{{f}_{liq}}{{F}_{v\_liq}} & T>0\ \ ℃\\ F_{{{v}_{\text{sn}ow}}}^{^\prime} & T<0\ \ ℃\\ \end{array} \right. $

(12)

F_{v _ sn ow}为降雪体积流量，T为气温，对F_{v _ sn ow}在时间上积分得到累积降雪预报量。

第四步，计算新降雪密度。新降雪密度等于累积降雪量除对应的液态相当体积。

$ {\rho _{{\rm{sn}}{\kern 1pt} ow}} = {A_{liq}}/A $

(13)

ρ_{sn ow}新降雪密度，A累积降雪预报量(即F_{v_snow}在时间上的积分)，A_liq 液态相当体积。

4 新降雪密度估算方法的发展评述 4.1 各估算方法的特点及局限性

设为常数法的突出特点就是简单、能够被迅速掌握和随时应用，且能达到45%以上的准确率(Roebber et al., 2003)，这也是尽管Abbe(1888)告诫19世纪天气观测员10:1这个简化的方法可能造成很大误差，但一百多年后的今天该方法仍经久不衰的原因。该方法也有着明显的不足，10:1仅代表了新降雪密度的一个平均值，任何进行过降雪观测的人都知道，在不同的降雪事件中新降雪密度是不同的，甚至在同一次风暴过程中新降雪密度也随时间而变化，已有研究表明，美国地区的新降雪密度变化范围为10~350 g·cm^-3；本文第二部分已说明新降雪密度并非气温一个影响因子，因此，Loth(1993)法和表 1气温和新降雪密度间的关系并非在所有情况下均适用，此外新降雪密度随气温的降低而持续减小是表 1的另一个缺陷，如本文第二部分所述，气温-15︒C左右是能观测到低密度降雪的理想温度条件，在气温更低时又回到高密度冰晶状态，因此，该方法会造成在低气温的条件下低估新降雪密度、高估降雪深度。

建立公式法估算新降雪密度考虑了2 m温度(气温)、地面温、湿、风等气象要素中的一到几个不等，这些公式基本均来自新降雪密度与地面气象要素之间的相关统计。该方法的特点是既计算简单又考虑了多种地面气象要素对新降雪密度的影响。该类新降雪密度公式均基于雪盖模式、陆面模式研究建立，这些研究领域主要关注冰雪、陆面、土壤、生物、水等近地面环境要素，也主要对地面气象要素进行观测、模拟，而对地面以上大气的研究较少、获得的观测与模拟信息也不足，这些情况导致了其发展的新降雪密度估算公式未考虑地面以上的气象要素。而如前所述，温、湿、风等气象要素的垂直分布是影响新降雪密度的重要因素，因此，缺乏对地面以上气象要素垂直分布的考虑成为现有的新降雪密度估算公式的重要缺陷。

后处理诊断法是加拿大气象专家从天气预报业务角度出发而建立的，其特点是基于观测与预报经验并结合了云微物理方面的知识，以温度为主线、湿度、风速为辅线，考虑了雪粒子在云中生长、云下变化的微物理过程，较为系统地考虑了降水类型及其对新降雪密度的影响，综合考虑了气象要素垂直分布。基于该地区281个地面温度小于0的降雪个例的检验证明该方法对超重雪、重雪、中重雪、轻雪、超轻雪密度的平均预报准确率超过80%(Dubé，2003)。但是，该方法限于对过冷却水滴形成条件及雪粒子与液相共存条件的认识不足，导致诊断吸积过程的标准非常简单，进而影响了诊断结果的准确性；由于地面温度观测数据较为稀疏甚至缺失，因此该方法中地面温度基本源于估计，这也降低了该方法在地面温度大于0情况下的新降雪密度诊断准确率；此外，该方法是基于加拿大魁北克地区33个观测站点1999—2002年冬季的观测建立的，应用效果的检验也是针对该区域进行，该方法对其他地区的适用性有待检验(Dubé，2003)。

微物理过程法基于整体微物理方案预报瞬时新降雪密度，其优点是：首先，该方法沿着降水的发展轨迹、水凝物粒子的生长历史，考虑其生长环境，基于所有诊断的微物理变量场，对每个格点或每个地方进行新降雪密度的预报。其次，该方法可预知任意一时间、地点的新降雪密度以及降雪类型的变化。但同时该方法也存在几方面的缺陷：第一，受计算能力限制，整体微物理方案中假定水凝物粒子尺寸分布服从特定的函数分布，导致该微物理过程即使有“完美”的初始条件，也无法或不能精确描述天气系统及其演变(陈葆德等，2013)。第二，假设雪粒子是以最大外形尺寸为直径的球形而低估新降雪密度。MY2方案中雪粒子的质量粒径关系(Kajikawa，1989；Thompson et al., 2008)结合可视雨滴谱仪图像说明绝大多数降落到地面的雪粒子为不规则的三维块状(Brandes et al., 2007)，这导致计算的瞬时新降雪密度实际上是一种低估或者应当被看做是对新降雪密度下限的一种估计。第三，霰粒子密度假设为固定值(0.4 k·cm^-3)影响新降雪密度预报准确性。实际上，霰粒子密度随着周围气温、液态水含量、霰粒子尺寸等有着较大的变化范围—0.05~0.7 g·cm^-3(Cober and List, 1993), 此外，霰是降雪(尤其是山区降雪)的重要组成部分，其密度的处理对于有明显结晶的降雪过程中新降雪密度的模拟效果有着重要的影响。第四，未考虑地面压实和雪粒子撞击碎裂过程而低估新降雪密度。如第二部分所述，新降雪密度受降水量影响较大，较大降水量的压实作用会增加新降雪密度(Ware et al., 2006)，而当风速较大时，其对于雪粒子的碎裂作用也会增加新降雪密度。

4.2 各估算方法间的承接关系

由上述各种估算方法的发展时间(表 5)和特点可清晰地看出，各估算方法间是上下承接的，新降雪密度估算是在新方法不断克服旧方法局限性的循环往复中逐步发展的。由表 5可见，新降雪密度的发展脉络较为清晰：(1)从建立估算方法的各研究领域看，气象领域在十九世纪到二十一世纪初均采用设为常数法，而雪盖和陆面领域自二十世纪末就开始进行新降雪密度估算公式的研究，并随着noah等陆面模式被引入天气预报模式，其发展的新降雪密度估算公式也间接地应用于气象领域，天气预报模式基于noah陆面模式诊断的雪密度输出积雪深度预报结果，而随着气象领域降雪预报业务的发展，已有的设为常数法和建立公式法已经不能满足降雪预报业务需求，气象领域开始从业务需求角度出发建立更为系统、全面的新降雪密度估算方法，目前已成为新降雪密度估算技术最为先进的领域，陆面和雪盖领域逐步走向引入气象领域的方法或结果。(2)从考虑气象要素的数量和范围看，新降雪密度估算从仅考虑地面气象要素到考虑地面与高空气象要素的综合影响，从片面走向全面，这是一个突破性进步，是得益于气象部门的先进、密集、管理科学的地面、高空观测业务及先进的数值天气预报模式。(3)从建立的方法看，新降雪密度估算方法的建立从简单的实验、统计逐步走向更为科学、客观的基于概念模型和物理机制，这一突破性进展也是由气象科学家基于数值天气预报模式实现的。

4.3 新降雪密度估算方法的发展方向展望

理论上，上述四类新降雪密度估算方法已经能够为降雪预报提供较为坚实的技术支撑，但是，目前冬季降雪预报业务仍然缺乏理想的降雪预报产品，理论与实际的偏差主要来源于两点：第一，并非各类估算方法均被广泛而深入的应用于降雪预报业务中，建立公式法目前只应用于陆面模式和雪盖模式中，后处理诊断方法和基于微物理过程法仍处于试验阶段，距离为各地区降雪预报业务服务仍需要较长的时间；第二，各估算方法的普适性尚未进行验证。当前降雪预报业务仍然主要依靠设为常数法。因此，新降雪密度的估算仍是一个需要深入探索和解决的重要气象问题。

基于目前的研究基础和现状，后处理诊断和基于微物理过程两种方法是基于降雪预报业务需求、从物理概念模型和物理机制角度建立的、综合考虑地面与高空气象要素的先进的新降雪密度估算方法，二者有着各自的特点和相对优势也有着各自难以克服的不足，如：业务高分辨率数值预报模式中使用总体云微物理参数化架构在未来20 a无法改变(陈葆德等，2013)，这一定程度上限制了基于微物理过程法的新降雪密度预报精度提升空间；地面温度大于0情况下新降雪密度的诊断是后处理诊断法的一个难点等等。因此，今后新降雪密度估算需要沿着这两个方向不断的尝试、探索，在两种方法的相互促进中逐步发展。

5 结论与讨论

本文围绕新降雪密度估算这一核心内容，简略回顾了新降雪密度估算中需要着重考虑的气象要素，并详细介绍了近几十年来国内外在新降雪密度估算方法方面的主要研究成果，在此基础上评述了几种常用估算方法的特点、局限性以及它们之间的承接联系，并对未来新降雪密度估算的发展方向进行展望。主要结论为：

(1) 温度、风速、湿度的垂直分布及太阳辐射、降水量是影响新降雪密度的重要气象要素。

(2) 目前被广泛应用的新降雪密度估算方法有设为常数法、建立公式法、后处理诊断法和基于微物理过程法等四类，且各具特点和局限性：设为常数法简单且能达到一定的准确率，但仅考虑气温一个气象要素而限制了其适用性。建立公式法考虑了多个地面气象要素，但缺乏对地面以上气象要素垂直分布的考虑。后处理诊断法着综合考虑了气象要素垂直分布并结合了云微物理知识，但存在吸积过程的标准过于简单、地面温度大于0时准确率相对不高等问题。基于微物理过程法能够对任意时间、地点进行新降雪密度的预报，但基于水凝物粒子尺寸分布、雪粒子形状、霰粒子密度等假设而影响精度。

(3) 新降雪密度估算方法的发展脉络较为清晰。最初由雪盖和陆面领域建立，后在气象领域发展、成熟，并被雪盖和陆面模式采用；考虑的气象要素从一个发展到多个、从仅考虑地面气象要素发展到考虑地面与高空气象要素的综合影响；建立的方法从简单的实验、统计发展到基于概念模型和物理机制。

基于目前的研究基础和现状，后处理诊断和基于微物理过程两种方法有着各自的特点和优势也有着难以克服的不足，今后新降雪密度估算需要沿着这两个方向不断的尝试、探索，在两种方法的逐步发展中相互促进，且需要使用我国降雪深度和降水量的观测，对估算方法和结果进行修订和评估。