2. 高原大气与环境四川省重点实验室, 成都 610225;
3. 中国科学院大学, 北京 100049
2. Plateau Atmosphere and Environment Key Laboratory of Sichuan Province, Chengdu 610225;
3. University of Chinese Academy of Sciences, Beijing 100049
大尺度系统及中尺度系统是大气中常见的两类天气系统,就中尺度天气系统而论,又可细分为α中尺度(水平范围在200 ~2 000 km),β中尺度(水平范围在20 ~200 km),γ中尺度系统(也可认为是小尺度,水平范围在不足1 ~20 km)。中尺度天气系统中,涡旋系统,如:台风,地方性低涡(西南涡、东北冷涡、中亚低涡等)及地方性气旋(如江淮气旋、黄淮气旋、蒙古气旋等),都可列为α中尺度(或者称为次天气尺度)天气系统,是中尺度动力学研究的主要天气系统,也是造成我国各地暴雨大风等高影响天气的重要影响系统。关于α中尺度的台风、低涡的研究较多,近年来也有相关的研究进展介绍。因此,本文虽然包含了部分较新的α中尺度低涡方面的研究结果回顾,但是有关台风和α中尺度低涡方面的主要进展不是论文的主要内容,本文重点针对中尺度对流涡(Meso-scale Convective Vortex,以下简称MCV)的动力学研究进展展开讨论。
王金鑫等(2014)曾对近30 a MCV的研究进展进行过总结,主要归纳了MCV的观测情况、MCV的统计及合成分析结果、MCV的平衡运动对新对流的影响、MCV结构概念模型、MCV对台风及其爆发性温带气旋生成的作用以及梅雨锋上MCV的分析等,统计和诊断分析的进展归纳较为全面,但是在MCV的动力学进展方面着墨不多。本文重点关注MCV的动力学研究进展,从有关MCV的产生及涡度方程、热量方程、能量方程以及中尺度垂直运动方程等方面来讨论近年来的进展,这是对已有进展回顾的重要补充,并且希望对解决MCV研究仍存在的科学问题提供有益参考。
1 中尺度对流涡的生成MCV最早是由Zhang和Fritsch (1988)提出的,此后,Raymond和Jiang (1990)提出了MCV的理论框架,并认为中尺度对流系统(Meso-scale Convective System,以下简称MCS)所造成的垂直方向上的非绝热加热异常是激发出中层中尺度气旋性环流的根本原因。Fritsch等(1994)以及Trier和Davis (2002)也认为MCV产生于MCS,并且MCV产生之后能激发出新对流以及组织形成新的MCS,新MCS又可反过来继续加强MCV。Conzemius和Montgomery (2010)以及Conzemius等(2007)也证明了MCV是由于MCS的非绝热作用产生。Chen和Frank (1993)以及Fritsch等(1994,图 1)则分别利用理想实验与观测验证了Raymond和Jiang (1990)的结论,并得出和完善了MCV的理论模型。后来,Davis和Galarneau (2009)进一步指出MCV与对流层中层发展起来的有组织的对流活动紧密相关,是具有高惯性稳定性的中尺度气旋性涡旋系统。Trier和Davis (2007)根据观测资料分析得出,强垂直运动使得MCV中心的顺切变方向为非绝热冷却,并且在MCV顺切变方向对高相当位温空气的水平输送会加强条件不稳定下的垂直运动,因此,在顺切变方向的右侧,中尺度上升运动最强、具有高相当位温并且风垂直切变增强,最有利于深对流的产生,新对流常在MCV顺切变方向形成。王金鑫等(2014)也指出,MCV不仅由对流活动产生,并且自身的平衡运动在有利环境条件下能激发新对流。Davis和Galarneau (2009)通过涡度倾向方程分析得出涡度辐合常常是MCV形成的主要原因,而扰动涡度的扰动通量作用则相对较小或局限于低层。目前比较明确的是,MCS导致的非绝热加热异常及深对流活动对MCV的触发有重要作用,但是对有关行星涡度的辐合、水平涡管的倾斜作用以及MCV与风垂直切变的关系仍需进一步定量分析(Bartels et al., 1997;Yu et al., 1999;Lai et al., 2011)。
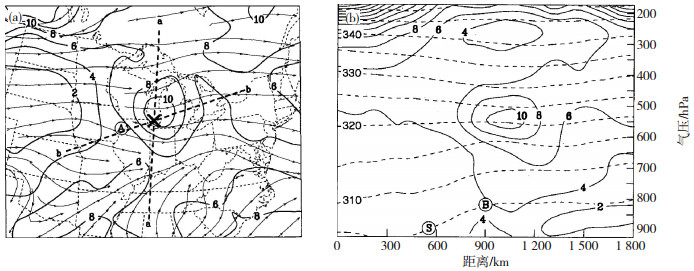
|
图 1 成熟时期的暖区中尺度涡结构特征(a.水平分布; b.过a中bb线的垂直剖面; 流线为地面流场, 等值线为525 hPa位涡, 虚线为位温“, X”指示涡中心) (Fritsch等, 1994) Fig. 1 The structure of MCV in mature stage (a. horizontal distribution, and b. vertical cross along bb line in Fig a. Stream line represents streamfield at surface, contour line represents potential vorticity at 525 hPa, dashed line represents potential temperatue, and X represents vertox center). |
MCV通常位于对流层中下层,垂直尺度能达到上千米(王金鑫等,2014),高空辐散、中层辐合、低空急流等是产生MCV的有利背景环流条件,MCV形成后对流层中层表现为明显的、持续存在的中尺度槽,MCV形成与对流的日循环有很强的相关性,但其生命史长短与其强度没有必然联系(James and Johnson, 2010),在MCV发展成为温带气旋的过程中,高空槽在涡旋区激发出的强上升运动有利于涡旋的快速增强(Boettcher and Wernli, 2011)。成熟的MCV最大风范围的直径约为100~300 km,但其影响范围常达到直径的2倍(Fritsch et al., 1994)。MCV内部中层有明显位涡(po⁃ tential vorticity,以下简称PV)极大值,高层为PV极小值(Raymond and Jiang, 1990;Davis and Trier, 2002;Trier and Davis, 2002;James and Johnson, 2010)。MCV通常为低层冷异常,高层暖异常,对流活动发展会导致高层暖异常减弱但低层冷异常维持(黄文娟,2017)。
2 中尺度对流涡的涡度方程在动力学上,对中尺度对流涡最主要的探讨是Davis和Galarneau (2009)给出传统的涡度方程,其相对涡度的局地变化可写为
| $ \frac{{\partial \zeta }}{{\partial t}} = - \mathit{\boldsymbol{V}} \cdot \nabla \eta - \omega \frac{{\partial \zeta }}{{\partial p}} - \frac{{\partial \omega }}{{\partial x}}\frac{{\partial v}}{{\partial p}} - \frac{{\partial \omega }}{{\partial y}}\frac{{\partial u}}{{\partial p}} + \mathit{\boldsymbol{k}} \cdot \nabla \times \mathit{\boldsymbol{F}} $ | (1) |
方程(1)中,ζ是相对涡度,V是水平风矢量,η是绝对涡度,ω是p坐标系统下的垂直速度,k是垂直方向单位矢量,F是摩擦力。
方程(1)进一步可整理写为
| $ \frac{{\partial \zeta }}{{\partial t}} = - \nabla \cdot \left( {\mathit{\boldsymbol{V}}\eta - \omega \mathit{\boldsymbol{k}} \times \frac{{\partial \mathit{\boldsymbol{v}}}}{{\partial p}} + \mathit{\boldsymbol{k}} \times \mathit{\boldsymbol{F}}} \right) = - \nabla \cdot \mathit{\boldsymbol{K}} $ | (2) |
方程(2)中,K是涡度通量矢量。可以看出,-▽· K只存在于水平平面内,即在气压坐标系标中的相对涡度变化没有垂直分量。
由于中尺度对流涡是一个涡度集中区,并不是一个单点上的涡度,所以用环量大小表示中尺度对流涡最为合适,也就是对方程(2)进行任一闭合区域迴路积分并利用散度原理(Gauss’s theorem)可得
| $ \begin{array}{l} \frac{{\partial C}}{{\partial t}} = - \oint_l \mathit{\boldsymbol{K}} \cdot \mathit{\boldsymbol{n}}{\rm{d}}l = \oint_l \eta \mathit{\boldsymbol{V}} \cdot \mathit{\boldsymbol{n}}{\rm{d}}l + \oint_l \omega \left( {\mathit{\boldsymbol{k}} \times \frac{{\partial \mathit{\boldsymbol{V}}}}{{\partial p}}} \right) \cdot \mathit{\boldsymbol{n}}{\rm{d}}l + \\ \;\;\;\;\;\;\;\oint_l {\left( {\mathit{\boldsymbol{k}} \times \mathit{\boldsymbol{F}}} \right)} \cdot \mathit{\boldsymbol{n}}{\rm{d}}l \end{array} $ | (3) |
方程(3)中,C就是环量,n是法向单位矢量,dl是环流积分,方程(3)意味着区域环量的变化只由垂直于区域边界的涡度通量矢量决定,不需要考虑内部区域的对流涡涡度,只考虑垂直于闭合区域边界的k分量就可以了,这样就大大简化了涡度方程在中尺度对流涡中的研究。方程(3)中,
| $ \frac{{\partial C}}{{\partial t}} = - \bar \eta \tilde \delta A - \oint_l {\eta '\mathit{\boldsymbol{V'}}} \cdot \mathit{\boldsymbol{n}}{\rm{d}}l + \oint_l \omega \left( {\mathit{\boldsymbol{k}} \times \frac{{\partial \mathit{\boldsymbol{V}}}}{{\partial p}}} \right) \cdot \mathit{\boldsymbol{n}}{\rm{d}}l $ | (4) |
方程(4)中,A是区域环线所围的面积,
| $ \frac{{\partial C}}{{\partial t}} = - \bar \eta \tilde \delta A + \oint_l \omega \left( {\mathit{\boldsymbol{k}} \times \frac{{\partial \mathit{\boldsymbol{V}}}}{{\partial p}}} \right) \cdot \mathit{\boldsymbol{n}}{\rm{d}}l $ | (5) |
由方程(5)可见,中尺度对流涡的强度取决于对流涡区域内的平均散度及涡边界上的垂直运动和风速垂直切变,因此,只要考虑环境场的风速垂直切变及在环境场的垂直运动和环流区域的平均散度就可以决定中尺度对流涡的强度。这也意味着,当环境风垂直切变大,垂直运动强时就会有中尺度对流涡形成发展,该过程总结得到如图 2的概念图(Davis and Galarneau,2009)。在我国最典型的过程就是,当西南风低空急流发展,就易造成水平风速的垂直风切变加大,加之地形抬升易造成垂直运动加强,所以在低空急流与地形结合时极易形成中尺度对流涡(周昆等,2007)。另外,在锋面附近,由于锋面上风的垂直切变很大,加之锋面抬升使垂直运动增强,也极易形成中尺度对流涡,我国长江流域梅雨锋上经常出现的中尺度对流涡旋(Chen and Chang, 1980;Chen and Zheng, 2004;朱爱军和潘益农,2007;王微等,2011;徐双柱等,2018)就与此有紧密关系。
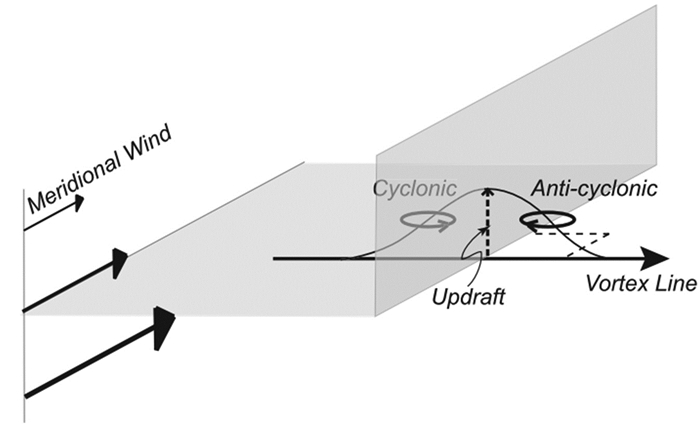
|
图 2 闭合区域内倾侧项引发中尺度对流涡旋形成的概念图(Davis and Galarneau, 2009) Fig. 2 Schematic of tilting contribution on the MCV in a circulation box (Davis and Galarneau, 2009). |
Li等(2016)研究变形场与锋生作用时,在涡度方程中导出了变形场与涡度变化的关系,具体表达式为
| $ {F_\zeta } = - \frac{{{\zeta _{\rm{h}}} \cdot {\nabla _p}{\theta _{\rm{e}}}}}{{2{\theta _{{\rm{ep}}}}}}\left| E \right|\cos 2\gamma $ | (6) |
方程(6)中,Fζ是涡度的时间变化,ζh是水平涡度,θe相当位温,
Weisman和Davis (1998)以及Davis和Galarneau (2009)推导的涡度方程没有考虑热力效应,这也意味着影响涡度发展的热力因素没有被考虑。后来Wu和Liu (1998)以及吴国雄(2001)推导了全型涡度方程为
| $ \begin{array}{l} \frac{{{\rm{d}}\zeta }}{{{\rm{d}}t}} = - \beta \mathit{\boldsymbol{V}} - \frac{\eta }{{{\theta _{{\rm{ep}}}}}}\frac{{\rm{d}}}{{{\rm{d}}t}}{\theta _{{\rm{ep}}}} - \frac{{\zeta {\theta _{\rm{e}}}}}{{{\theta _{{\rm{ep}}}}}}\frac{{\rm{d}}}{{{\rm{d}}t}}\left| {{\nabla _p}{\theta _{{\rm{ep}}}}} \right| - \frac{{\left| {{\nabla _p}{\theta _{\rm{e}}}} \right|}}{{{\theta _{{\rm{ep}}}}}}\frac{{\rm{d}}}{{{\rm{d}}t}}\zeta {\theta _{\rm{e}}} + \\ \;\;\;\;\;\;\;\;\;\frac{1}{{{\theta _{{\rm{ep}}}}}}\nabla \times \mathit{\boldsymbol{F}} \cdot \nabla {\theta _{\rm{e}}} + \frac{1}{{{\theta _{{\rm{ep}}}}}}\eta \cdot \nabla {Q_m} \end{array} $ | (7) |
方程(7)中,β是地转参数,ζθe是水平涡度矢量在▽pθe方向上的投影值,η是绝对涡度,Qm为非绝热加热。忽略外源加热与摩擦,方程(7)便为
| $ \begin{array}{l} \frac{{\partial \zeta }}{{\partial t}} = - \mathit{\boldsymbol{V}} \cdot \nabla \zeta - \beta \mathit{\boldsymbol{V}} - \frac{{{\zeta _a}}}{{{\theta _{{\rm{ep}}}}}}\frac{{\rm{d}}}{{{\rm{d}}t}}{\theta _{{\rm{ep}}}} - \frac{{\zeta {\theta _{\rm{e}}}}}{{{\theta _{{\rm{ep}}}}}}\frac{{\rm{d}}}{{{\rm{d}}t}}\left| {{\nabla _p}{\theta _{\rm{e}}}} \right| - \\ \;\;\;\;\;\;\;\;\frac{{\left| {{\nabla _p}{\theta _{\rm{e}}}} \right|}}{{{\theta _{{\rm{ep}}}}}}\frac{{\rm{d}}}{{{\rm{d}}t}}\zeta {\theta _{\rm{e}}} \end{array} $ | (8) |
方程(7)中,对于中尺度系统忽略β项,则有
| $ \frac{{\partial \zeta }}{{\partial t}} = - \mathit{\boldsymbol{V}} \cdot \nabla \zeta - \frac{{{\zeta _a}}}{{{\theta _{{\rm{ep}}}}}}\frac{{\rm{d}}}{{{\rm{d}}t}}{\theta _{ep}} - \frac{{\zeta {\theta _{\rm{e}}}}}{{{\theta _{{\rm{ep}}}}}}\frac{{\rm{d}}}{{{\rm{d}}t}}\left| {{\nabla _p}{\theta _{\rm{e}}}} \right| - \frac{{\left| {{\nabla _p}{\theta _{\rm{e}}}} \right|}}{{{\theta _{{\rm{ep}}}}}}\frac{{\rm{d}}}{{{\rm{d}}t}}\zeta {\theta _{\rm{e}}} $ | (9) |
方程(9)等号右边第一项是相对涡度的平流项,在一个固定的地方,大气平流导致的涡度如果没有明显的辐合,涡度会被平流而不能得以保持,所以这不是影响涡度发展的主要项。右边第二项反映了等熵面倾斜的总变化对涡度发展的贡献,是影响涡度发展的主要项。正如Zhang (1992)最初指出蒸发融化等原因造成的热力变化引起了等熵面的倾斜,从而会造成涡度发展,这部分在传统的涡度方程中没有体现。而方程(9)等号右边的第三项是与锋生函数
由前文可知,许多研究表明MCV是由于MCS非绝热加热作用产(Raymond and Jiang,1990;Zhang,1992;Chen and Frank,1993;1Fritsch et al.,1994;Conzemius et al.,2007;Conzemius and Montgomery,2010),因此热量收支研究也是对MCV研究中非常重要的环节。Chen和Frank(1993)给出sigma坐标下的热量方程
| $ \begin{array}{l} \frac{{\partial T}}{{\partial t}} = - \mathit{\boldsymbol{V}} \cdot \nabla T - \omega \left( {\frac{{\partial T}}{{\partial p}}} \right) + R{T_v}\omega {\left[ {{C_p}\left( {1 + 0.8{q_v}} \right)\left( {{p^*}\sigma + {p_t}} \right)} \right]^{ - 1}} + \\ \;\;\;\;\;\;\;{Q_{\rm{c}}} + {Q_{{\rm{nc}}}} + {F_{\rm{h}}}T + {F_v}T \end{array} $ | (10) |
方程(10)中,T为温度,-V·▽T代表温度的水平平流,
黄文娟(2017)在方程(10)的基础上加入辐射加热项,将热量方程改写为
| $ \begin{array}{l} \frac{{\partial T}}{{\partial t}} = - \mathit{\boldsymbol{V}} \cdot \nabla T - \omega \left( {\frac{{\partial T}}{{\partial p}} - \frac{{R{T_v}}}{{{C_p}\left( {1 + 0.8{q_v}} \right)p}}} \right) + {Q_{\rm{c}}} + \\ \;\;\;\;\;\;{Q_{{\rm{nc}}}} + {Q_{\rm{r}}} \end{array} $ | (11) |
方程(11)中,Qr为湿辐射加热。利用方程(11)诊断分析了一次MCV发生发展及消亡时期热量收支的情况,比较不同时期各项的作用,解释了MCV发生发展及消亡过程中涡内温度垂直分布的原因,并指出MCV的触发与MCS有组织的发展导致大量潜热释放和风场的低层辐合高层辐散的动力配置有关。
Nicholls等(2018)从水物质相态变化角度推导适合利用数值模式结果计算的净非绝热加热诊断方程
| $ \delta {Q_m} = {L_c}\delta {r_1} + \left( {{L_c} + {L_{\rm{f}}}} \right)\delta {r_{\rm{i}}} $ | (12) |
方程(12)中,δQm表示模式一个时间步长、一个格点体积内单位质量空气释放或吸收的净潜热,δrl为液态水混合比的变化,δri为冰的混合比的变化,Lc为凝结潜热,Lf为融合潜热,并通过对原有诊断方程增加源项
除了涡度方程以及热量方程,还有学者从能量学的角度对中尺度涡的能量收支转化演变进行动力诊断分析研究。Edmon (1978)推导出有效位能收支方程
| $ \begin{array}{l} \frac{{\partial A}}{{\partial t}} = \frac{1}{{\sigma g}}\int_\sigma {\int_{{p_{\rm{u}}}}^{{p_{\rm{s}}}} N } Q{\rm{d}}p{\rm{d}}s + \frac{1}{{\sigma g}}\int_\sigma {\int_{{p_{\rm{u}}}}^{{p_{\rm{s}}}} N } \omega a{\rm{d}}p{\rm{d}}s - \\ \;\;\;\;\;\;\;\;\frac{{{c_p}}}{{\sigma g}}\int_\sigma {\int_{{p_{\rm{u}}}}^{{p_{\rm{s}}}} {\left( {N\mathit{\boldsymbol{V}} \cdot {\nabla _p}T} \right)} } {\rm{d}}p{\rm{d}}\sigma - \frac{{{c_p}}}{{\sigma g}}\int_\sigma {\int_{{p_{\rm{u}}}}^{{p_{\rm{s}}}} N } \omega \frac{{\partial T}}{{\partial p}}{\rm{d}}p{\rm{d}}\sigma + \\ \;\;\;\;\;\;\;\;\frac{{{c_p}}}{{\sigma g}}\int_\sigma {\int_{{p_u}}^{{p_s}} T } \frac{{\partial N}}{{\partial t}}{\rm{d}}p{\rm{d}}\sigma + \frac{{{c_p}}}{{\sigma g}}\int_\sigma {{N_{\rm{s}}}} {T_{\rm{s}}}\frac{{\partial {p_{\rm{s}}}}}{{\partial t}}{\rm{d}}\sigma \end{array} $ | (13) |
方程(13)中,A表示有效位能,
Chen等(1978)得出动能收支方程
| $ \begin{array}{l} \frac{{\delta k}}{{\delta t}} = - J\left( {\varphi ,k} \right) + \omega \frac{{\partial k}}{{\partial p}} + C \cdot \nabla k - J\left( {\varphi ,\phi } \right) + \\ \;\;\;\;\;\;\;\;\nabla \chi \cdot \nabla \phi + \nabla \cdot \mathit{\boldsymbol{F}} \end{array} $ | (14) |
Dimego和Bosart(1982)以及Ding和Liu(1986)对方程(14)进行了单位体积空气柱的积分后得到
| $ \begin{array}{l} \frac{{\delta K}}{{\delta t}} = \frac{1}{g}\int_{{p_{\rm{u}}}}^{{p_{\rm{b}}}} {\left[ { - \overline {\overline {J(\varphi ,k)} } + \overline {\overline {\mathit{\boldsymbol{V}} \cdot \nabla k} } - \frac{l}{s}\overbrace {k{v_\chi }a}^{} - \frac{{\partial \overline{\overline {\omega k}} }}{{\partial p}}} \right]{\rm{d}}p} + \\ \;\;\;\;\;\;\;\;\;\frac{1}{g}\int_{{p_{\rm{u}}}}^{{p_{\rm{b}}}} {\left[ { - \overline {\overline {J(\varphi ,k)} } + \overline {\overline {\nabla \chi \cdot \nabla \phi } } } \right]{\rm{d}}p + D\left( k \right)} \end{array} $ | (15) |
方程(15)中,
| $ \begin{array}{l} H\left( {{K_\chi }{K_\psi }} \right) = f\nabla \chi \nabla \psi + {\nabla ^2}\psi \chi \cdot \nabla \psi + \frac{{{{\left| {\nabla \psi } \right|}^2}}}{2}{\nabla ^2}\chi - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\omega \left( { - {V_\psi } \cdot \nabla \frac{{\partial \chi }}{{\partial p}}} \right) \end{array} $ | (16) |
方程(16)中,H为动能倾向,ψ表示流函数,χ表示势函数,Kχ为辐散风动能,Kψ为旋转风动能。方程(16)等号右边第一项为平流项,第二项为相对涡度项,第三项为辐散项,第四项为垂直速度项。Fu等(2011)利用该方程诊断分析了西南涡内辐散风动能与旋转风动能间的转换关系,同时讨论了涡内有效位能的变化与动能转换之间的关系,指出动能的生成和能量平流是涡内最重要的能量源。
冉令坤等(2014)推导出涡度拟能方程
| $ \frac{{\partial {\zeta ^2}}}{{\partial t}} = {F_{s,\zeta E}} + {F_{d,\zeta E}} + {F_{d,\zeta D}} $ | (17) |
其中
| $ \begin{array}{l} {F_{s,\zeta E}} = - \mathit{\boldsymbol{V}} \cdot \nabla \left[ {{{\left( {\frac{{\partial v}}{{\partial x}}} \right)}^2} + {{\left( {\frac{{\partial u}}{{\partial y}}} \right)}^2}} \right] - 2\left[ {{{\left( {\frac{{\partial v}}{{\partial x}}} \right)}^2} + {{\left( {\frac{{\partial u}}{{\partial y}}} \right)}^2}} \right] - \\ \;\;\;\;\;\;\;\;2\left[ {\frac{{\partial v}}{{\partial x}}\frac{{\partial \omega }}{{\partial x}}\frac{{\partial v}}{{\partial p}} + \frac{{\partial u}}{{\partial y}}\frac{{\partial \omega }}{{\partial y}}\frac{{\partial u}}{{\partial p}}} \right] + 2\beta v\frac{{\partial u}}{{\partial y}} \end{array} $ | (18) |
| $ \begin{array}{l} {F_{s,\zeta E}} = - \mathit{\boldsymbol{V}} \cdot \nabla \left( { - 2\frac{{\partial v}}{{\partial x}}\frac{{\partial u}}{{\partial y}}} \right) + 2\frac{{\partial v}}{{\partial x}}\frac{{\partial u}}{{\partial y}}D + \\ \;\;\;\;\;\;\;\;2\left[ {\frac{{\partial v}}{{\partial x}}\frac{{\partial \omega }}{{\partial y}}\frac{{\partial u}}{{\partial p}} + \frac{{\partial u}}{{\partial y}}\frac{{\partial \omega }}{{\partial x}}\frac{{\partial v}}{{\partial p}}} \right] - 2\beta v\frac{{\partial v}}{{\partial x}}\frac{{\partial u}}{{\partial y}} \end{array} $ | (19) |
| $ {F_{s,\zeta D}} = - 2f\zeta D + 2\frac{{\partial v}}{{\partial x}}\frac{{\partial u}}{{\partial y}}D $ | (20) |
Fs, ζE为涡度拟能-变形能量相同项,表示涡度拟能与变形能量局地同步发展;D为散度;Fd, ζE为涡度拟能-变形能量转换项,Fd, ζE > 0代表变形能量向涡度拟能转化;Fd, ζD为涡度拟能-散度能量转换项,Fd, ζD > 0代表散度能量向涡度拟能转化。冉令坤等(2014)利用涡度拟能方程讨论了涡内动能的变化与转换,讨论了有效位能的变化,进一步应用到登陆台风涡度拟能收支揭示台风涡旋的强弱演变。
Yang等(2017)根据中尺度涡的影响系统中的能量异常,推出了能量守恒方程为
| $ \frac{{\partial Z}}{{\partial t}} + \nabla \left[ {\mathit{\boldsymbol{V}}\left( {Z + P} \right)} \right] = 0 $ | (21) |
这里
| $ \frac{{\partial Z}}{{\partial t}} = - \nabla \left[ {\mathit{\boldsymbol{V}}\left( {Z + P} \right)} \right] $ | (22) |
由方程(22)式可见,涡中总能量的局地增强与减弱的变化取决于总能量平流与气压做功的辐散与辐合,如果出现辐合则使涡内能量增强,有利于涡的发展。
这些能量学的研究,尤其是涡度拟能方程和变形拟能方程,为诊断中尺度涡的发展与变化增加了新的内容。
5 中尺度垂直运动诊断和垂直运动方程垂直运动强是中尺度相对大尺度最显著的特征之一。以往对垂直运动的估计有几种不同的方法,主要有连续性方程计算方法,即利用P坐标系中的连续性方程,通过积分而得到垂直运动。这种方法有一定缺陷,因为垂直运动满足了连续性方程但是不一定满足热力方程和动量方程。真正垂直运动的计算还应从动量方程出发而求得。由于在任何短的瞬间,运动可以看成定常的,即有
| $ \frac{{{\rm{d}}\mathit{\boldsymbol{V}}}}{{{\rm{d}}t}} + f\mathit{\boldsymbol{k}} \times \mathit{\boldsymbol{V}} = - {\alpha _0}\nabla p' + B\mathit{\boldsymbol{k}} $ | (23) |
可近似写为
| $ \mathit{\boldsymbol{V}} \cdot \nabla \mathit{\boldsymbol{V}} + f\mathit{\boldsymbol{k}} \times \mathit{\boldsymbol{V}} = - {\alpha _0}\nabla p' + B\mathit{\boldsymbol{k}} $ | (24) |
其中,α0为比热,Bk为垂直方向的浮力。
方程(24)两边同时点乘速度方向上的位移dr,于是有
| $ \left( {\mathit{\boldsymbol{V}} \cdot \nabla \mathit{\boldsymbol{V}}} \right) \cdot {\rm{d}}\mathit{\boldsymbol{r}} + (f\mathit{\boldsymbol{k}} \times \mathit{\boldsymbol{V}}) \cdot {\rm{d}}\mathit{\boldsymbol{r}} = - {\alpha _0}\frac{{\partial p'}}{{\partial z}} \cdot {\rm{d}}\mathit{\boldsymbol{r}} + B{\rm{d}}z $ | (25) |
或写为
| $ \nabla \left( {\frac{1}{2}\mathit{\boldsymbol{V}} \cdot \mathit{\boldsymbol{V}}} \right) \cdot {\rm{d}}\mathit{\boldsymbol{r}} + \left[ {\left( {\nabla \times \mathit{\boldsymbol{V}}} \right) \times \mathit{\boldsymbol{V}}} \right] \cdot {\rm{d}}\mathit{\boldsymbol{r}} = - {\alpha _0}p' + B{\rm{d}}z $ | (26) |
| $ {\rm{即d}}\left( {\frac{1}{2}{\mathit{\boldsymbol{V}}^2}} \right) = - {\alpha _0}{\rm{d}}p' + B{\rm{d}}z $ | (27) |
两边积分得
| $ \int {d\left( {\frac{1}{2}{\mathit{\boldsymbol{V}}^2}} \right)} + {\alpha _0}\int {{\rm{d}}p'} - \int {B{\rm{d}}z} = 0 $ | (28) |
从方程(28)可知
| $ \frac{1}{2}{\left| {{\mathit{\boldsymbol{V}}^2}} \right|_{{\rm{end}}}} - \frac{1}{2}{\left| {{\mathit{\boldsymbol{V}}^2}} \right|_{{\rm{initial}}}} + {\alpha _0}{{p'}_{{\rm{end}}}} - {\alpha _0}{{p'}_{{\rm{initial}}}} - \int {B{\rm{d}}z} = 0 $ | (29) |
对初始远离积云发展区的运动的空气质点,可认为该处初始扰动气压p' initial = 0,则初始时也有B=0。方程(29)可简化为
| $ \frac{1}{2}\left| {{\mathit{\boldsymbol{V}}^2}} \right| - \frac{1}{2}{\left| {{\mathit{\boldsymbol{V}}^2}} \right|_{{\rm{initial}}}} + {\alpha _0}p' = 0 $ | (30) |
得到
| $ {\alpha _0}p' = \frac{1}{2}{\left| {{\mathit{\boldsymbol{V}}^2}} \right|_{{\rm{initial}}}} - \frac{1}{2}\left| {{\mathit{\boldsymbol{V}}^2}} \right| $ | (31) |
对在从对流层低层向对流层中层运动的空气质点,有理由认为|V |的值大于|V |initial的值,因为空气质点在保持动量守恒的过程中,从低层走向高层时,空气的密度明显减小,而迫使质点的速度加大,以满足动量守恒,于是可推测到
| $ \frac{1}{2}\left| {{\mathit{\boldsymbol{V}}^2}} \right| = \frac{1}{2}{\left| {{\mathit{\boldsymbol{V}}^2}} \right|_{{\rm{initial}}}} + \alpha \left| {{\mathit{\boldsymbol{V}}^2}} \right| $ | (32) |
其中,α为0 < α < 1的系数。
将方程(32)代入到方程(31)得到
| $ {\alpha _0}p' = \frac{1}{2}\left| {{\mathit{\boldsymbol{V}}^2}} \right| - \frac{1}{2}{\left| {{\mathit{\boldsymbol{V}}^2}} \right|_{{\rm{initial}}}} - \alpha \left| {{\mathit{\boldsymbol{V}}^2}} \right| = - \alpha \left| {{\mathit{\boldsymbol{V}}^2}} \right| $ | (33) |
将方程(33)代入到方程(29),并认为是在对流区内,则有
| $ \frac{1}{2}w_{\rm{m}}^2 = \frac{1}{2}{\left| {{\mathit{\boldsymbol{V}}^2}} \right|_{{\rm{initial}}}} + \alpha \left| {{\mathit{\boldsymbol{V}}^2}} \right| + \int {B{\rm{d}}z} $ | (34) |
在对流层中层CAPE可表示为
| $ CAPE = \int_{{\rm{ch}}}^{{\rm{pmh}}} {B{\rm{d}}z} $ | (35) |
其中,pmh为大气中层高度,lch为自由对流高度,故有
| $ w_{\rm{m}}^2 = 2CAPE + {\left| {{\mathit{\boldsymbol{V}}^2}} \right|_{{\rm{initial}}}} + \alpha \left| {\mathit{\boldsymbol{V}}_m^2} \right| $ | (36) |
由此可以看出,强对流系统中垂直运动w的值应如方程(36)表达,同时它也应当满足连续性方程。由于对流层中层风速较大,所以wm的值明显取决于对流层中层水平运动的风速Vm。由此可见,对流层中层大风的出现是强对流发展的信号,也是一种预报指标。再者,由于wm应当满足连续性方程,强垂直运动必然造成大气中层及其以下的强辐合,因此中层以下的强辐合区也是一个预报强对流和积云发展的重要指标。
仅仅关心垂直运动还不够,还需要知道影响垂直运动变化的原因,这就涉及到垂直运动方程。基于准地转理论的垂直运动方程被大量使用到了天气尺度系统的性质、结构和演变研究上(Strahl and Smith, 2001;Dixon et al. 2003;Gray and Dacre, 2006)等。但是,准地转假设忽略了很多对次天气尺度和中尺度系统有重要影响的因素,比如非地转风、静力稳定度的水平变化等的影响,以及非绝热加热的作用(Pauley and Nieman, 1992)。中尺度最显著的特征就是其内部垂直运动强,与大尺度运动中的垂直运动相比有量级上的差异。垂直速度是反映大气对流运动发生发展过程中的一个非常重要的物理量,但是又无法通过观测得到,只能用诊断方法而得,而垂直运动的诊断,尤其是强垂直运动的诊断,一直是大气科学研究中比较棘手的问题。大尺度运动是在准地转框架下演变,所以对应的是准地转垂直运动方程,即通常所说的ω方程,这对于中尺度系统就不适用了。因此,假设更少的广义垂直运动方程逐渐建立起来(Tarbell et al. 1981;Hirschberg and Fritsch, 1991;Raisanen,1995;Rantanen,2017)。Raisanen (1995)给出的广义垂直运动方程,其表达式为
| $ \begin{array}{l} {\nabla ^2}\left( {\sigma \omega } \right) +\\ f\frac{\partial }{{\partial p}}\left[ {\left( {\zeta + f} \right)\frac{{\partial \omega }}{{\partial p}} - f\frac{\partial }{{\partial p}}\left( {\frac{{\partial \omega }}{{\partial p}}\omega } \right) + f\frac{\partial }{{\partial p}}\left[ {\mathit{\boldsymbol{k}} \cdot \left( {\frac{{\partial \mathit{\boldsymbol{V}}}}{{\partial p}} \times \nabla \omega } \right)} \right] = f\frac{\partial }{{\partial p}}\left[ {\mathit{\boldsymbol{V}} \cdot \left( {\zeta + f} \right)} \right]} \right] +\\ \frac{R}{P}{\nabla ^2}\left( {\mathit{\boldsymbol{V}} \cdot \nabla T} \right) - f\frac{\partial }{{\partial p}}\left( {\mathit{\boldsymbol{k}} \cdot \nabla \times \mathit{\boldsymbol{F}}} \right) - \frac{R}{{{c_p}p}}{\nabla ^2}Q + \left[ {f\frac{\partial }{{\partial p}}\left( {\frac{{\partial \zeta }}{{\partial t}}} \right) + \frac{R}{P}{\nabla ^2}\frac{{\partial T}}{{\partial t}}} \right] \end{array} $ | (37) |
该方程中体现了非平衡项的作用,Q为单位质量非绝热加热率。方程(37)可以用来诊断中尺度的垂直运动,但是没有考虑地图投影造成的变形,影响了基于中尺度数值模式结果的垂直运动计算效果。
目前,高分辨数值模式预报已经得到广泛应用,模式多物理过程参数的输出,使获得观测资料中难获得的一些量成为可能,如非绝热加热率、摩擦等。但是,计算垂直运动时,理论上的动热力过程难以与模式输出直接结合起来。所以,还需要一个在高分辨率模式框架下可用的广义垂直运动方程求解方案来定量计算中尺度的垂直运动(Clough et al., 1996)。为了解决这个问题,李驰钦(2018)再次给出如下的广义垂直运动方程
| $ \begin{array}{l} {m^2}{\nabla ^2}\left( {\sigma \omega } \right) + \\f\left( {\zeta + f} \right)\frac{{{\partial ^2}\omega }}{{\partial {p^2}}} - f\frac{{{\partial ^2}}}{{\partial {p^2}}}\omega + f\frac{\partial }{{\partial p}}\left[ {\mathit{\boldsymbol{k}} \cdot \left( {\frac{{\partial \mathit{\boldsymbol{V}}}}{{\partial p}} \times m\nabla \omega } \right)} \right] = mf\frac{\partial }{{\partial p}}\left[ {\mathit{\boldsymbol{V}} \cdot \nabla \left( {\zeta + f} \right)} \right] + \\{m^2}\frac{R}{P}{\nabla ^2}\left( {m\mathit{\boldsymbol{V}} \cdot \nabla T} \right) - {m^2}\frac{R}{{{c_p}p}}{\nabla ^2}Q - f\frac{\partial }{{\partial p}}\left[ {{m^2}\mathit{\boldsymbol{k}} \cdot \left( {\nabla \times \frac{\mathit{\boldsymbol{F}}}{m}} \right)} \right] + f\frac{\partial }{{\partial p}}\left( {\frac{{\partial \zeta }}{{\partial t}}} \right) +\\ {m^2}\frac{R}{p}{\nabla ^2}\left( {\frac{{\partial T}}{{\partial t}}} \right) \end{array} $ | (38) |
方程(38)与Raisanen (1995)和Rantanen等(2017)的方程基本相同,但考虑了地图投影造成的变形作用,可直接用于中尺度模式输出结果的垂直运动的定量诊断。利用该方程诊断的中尺度模式WRF模拟输出的一次北方气旋新生个例引起的垂直运动(图 3,李驰钦,2018)表明,广义垂直运动方程诊断的垂直速度图 3广义垂直运动方程(38)求得的涡度垂直速度与模式原有诊断速度分布基本一致(图 3a、b),但由于广义垂直运动方程考虑了地图投影变形效应,且对中高层大气的非绝热加热项的反应和对流层上下边界作用的动热力作用效果较好,在对垂直运动的描述上优于准地转运动方程,在涡旋发展强盛的地方,广义垂直运动方程诊断的上升运动明显强于模式原有的结果(图 3c)。此外,这两项与准地转垂直运动方程计算的垂直速度的比较还表明(图 3d),准地转方程中由于没有包含非绝热项,仅有涡度与温度平流项,其量级远小于广义垂直运动方程和WRF模式输出后诊断得到的垂直速度,表明此次过程中非绝热加热项在引发垂直运动强度上的主导作用。
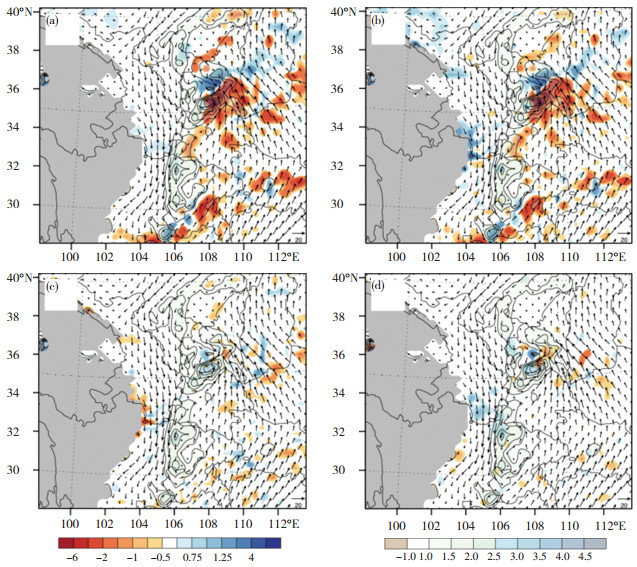
|
图 3 广义垂直运动方程(38)求得的涡度垂直速度(a), WRF输出的垂直速度(b), 图(a)的垂直速度与图(b)的垂直速度之差(c), 准地转垂直速度(d)和风场(矢量, 单位: m·s-1)分布(阴影为垂直运动, 单位: Pa·s-1) (李驰钦, 2018) Fig. 3 Distribution of (a) the vertical velocity from Eq.(38), (b) vertical velocity output from WRF, (c) difference between (a) and (b), and (d) QG vertical velocity and wind (vector, unit: m·s-1) (shadow represents vertical velocity, unit:Pa·s-1) (Li, 2018). |
虽然个例的诊断效果显著,但是该广义垂直运动方程一定程度上反映出了中尺度垂直运动的非地转性质,但其仍然是基于P坐标推导得到,本质上还是应用了静力近似,所以对发展旺盛的中尺度运动的适用性还需加强。
6 讨论与展望在中尺度对流系统中,大多数或说几乎均存在着中尺度对流涡,切变线上也会存在涡旋,所以中尺度涡旋是中尺度系统中最典型的代表,这就是为什么本文以中尺度对流涡为主线来回顾其动力学研究进展。中尺度动力学问题的研究内容很多,除了中尺度对流性涡旋之外,还有重力波、中尺度切变线、中尺度锋面与急流等,但中尺度中最主要的还是中尺度涡旋,无论是中尺度台风、地方气旋(如江淮气旋,西南涡、高原涡以及中亚低涡等),均是中尺度涡旋系统,这些涡旋系统往往是我国不同区域的直接的致灾天气系统。因此,未来中尺度涡的动力学研究仍会方兴未艾。可以预见,经过探索和努力,在中尺度涡的动力学研究方面也会有新的突破。存在的问题和未来可预期的突破,列举如下:(1)对有关行星涡度的辐合、水平涡管的倾斜作用以及MCV与风垂直切变的关系的定量分析;(2)基于非静力的中尺度垂直运动方程的理论完善、计算和效果检验;(3)螺旋度可用于计算水平涡旋在环境场中向垂直方向倾斜时涡旋在雷暴上升气流中的发展趋向,测量旋转上升气流的垂直风切变(孙淑清和周玉淑,2007),可以用于中尺度涡的发展与演变的研究,因此需要更多与此相关的研究工作;(4)已有的半平衡动力学理论(Xu and Cao, 2012)还停留在理论阶段,但是通过努力,有望用于中尺度涡的研究并可发展出一套反演次级环流的新方法;(5)一个较为新颖的确定台风涡旋中心的动力学方法(Xu et al., 2015)也可拓展用于确定中尺度涡中心位置的研究。这些新的手段与工具可为中尺度涡动力学的研究展现新的繁荣带来希望。
陈联寿, 许映龙. 2017. 中国台风特大暴雨综述[J]. 气象与环境科学, 40(1): 3-10. |
黄文娟.2017.江淮梅雨锋上典型中尺度对流涡旋诊断与模拟[D].华东师范大学
|
李驰钦.2018.位涡反演和广义垂直运动方程的应用研究[D].中国科学院大学
|
李国平, 陈佳. 2018. 西南涡及其暴雨研究新进展[J]. 暴雨灾害, 37(4): 293-302. DOI:10.3969/j.issn.1004-9045.2018.04.001 |
冉令坤, 李娜, 崔晓鹏. 2014. 登陆台风莫拉克(2009)的涡度拟能收支分析[J]. 气象学报, 72(6): 1118-1134. |
孙淑清, 周玉淑. 2007. 近年来我国暴雨中尺度动力分析研究进展[J]. 大气科学, 31(6): 1171-1188. DOI:10.3878/j.issn.1006-9895.2007.06.13 |
王东海, 钟水新, 刘英, 等. 2007. 东北暴雨的研究[J]. 地球科学进展, 22(6): 549-560. DOI:10.3321/j.issn:1001-8166.2007.06.001 |
王金鑫, 潘益农, 束宇, 等. 2014. 中尺度对流涡旋(MCV)近30 a来的研究进展[J]. 气象科学, 34(3): 343-354. |
王微, 潘益农, 束宇. 2011. 中国东部夏季中尺度对流系统以及中尺度对流涡旋的特征[J]. 南京大学学报(自然科学版), 47(6): 692-702. |
吴国雄. 2001. 全型涡度方程和经典涡度方程比较[J]. 气象学报, 59(4): 385-392. |
徐双柱, 陈静静, 王青霞. 2018. 南岳山、庐山高山站风场对长江流域梅雨锋暴雨的指示作用[J]. 暴雨灾害, 37(3): 213-218. DOI:10.3969/j.issn.1004-9045.2018.03.003 |
周昆, 潘益农, 王东勇, 等. 2007. 大别山区地形对春季冷锋附近中尺度对流系统影响的数值模拟研究[J]. 南京大学学报(自然科学版), 43(5): 535-543. DOI:10.3321/j.issn:0469-5097.2007.05.012 |
朱爱军, 潘益农. 2007. 中国东部地区一个中尺度对流涡旋的涡度收支分析[J]. 南京大学学报(自然科学版), 43(3): 260-269. |
Bartels D L, Brown J M, Tollerud E I. 1997. Structure of a midtropospheric vortex induced by a mesoscale convective system[J]. Monthly Weather Review, 125(2): 193-211. DOI:10.1175/1520-0493(1997)125<0193:SOAMVI>2.0.CO;2 |
Boettcher M, Wernli H. 2011. Life Cycle Study of a Diabatic Rossby Wave as a Precursor to Rapid Cyclogenesis in the North Atlantic-Dynamics and Forecast Performance[J]. Monthly Weather Review, 139(6): 1861-1878. DOI:10.1175/2011MWR3504.1 |
Chen M, Zheng Y G. 2004. Vorticity budget investigation of a simulated long-lived mesoscale vortex in South China[J]. Advances in Atmospheric Sciences, 21(6): 928-940. DOI:10.1007/BF02915595 |
Chen S Y, Frank W M. 1993. A numerical study of the genesis of extratropical convective mesovortices evolution and dynamics[J]. Journal of the Atmospheric Sciences, 50(15): 2401-2426. DOI:10.1175/1520-0469(1993)050<2401:ANSOTG>2.0.CO;2 |
Chen T C, Alpert J C, Schlatter T W. 1978. Effects of divergent and nondivergent winds on kinetic-energy budget of a mid-latitude cyclone-case study[J]. Monthly Weather Review, 106(4): 458-468. DOI:10.1175/1520-0493(1978)106<0458:TEODAN>2.0.CO;2 |
Chen T J, Chang CP. 1980. The structure and vorticity budget of an early summer monsoon through (Mei-Yu) over southeastern china and japan[J]. Monthly Weather Review, 108(7): 942-953. DOI:10.1175/1520-0493(1980)108<0942:TSAVBO>2.0.CO;2 |
Clough S A, Davitt C S, Thorpe A J. 1996. Attribution concepts applied to the omega equation[J]. Quarterly Journal of the Royal Meteorological Society, 122(536): 1943-1962. DOI:10.1002/qj.49712253610 |
Conzemius R J, Montgomery M T. 2010. Mesoscale convective vortices in multiscale, idealized simulations: dependence on background state, interdependency with moist baroclinic cyclones, and comparison with bamex observations[J]. Monthly Weather Review, 138(4): 1119-1139. DOI:10.1175/2009MWR2981.1 |
Conzemius R J, Moore R W, Montgomery M T, et al. 2007. Mesoscale convective vortex formation in a weakly sheared moist neutral environment[J]. Journal of the Atmospheric Sciences, 64(5): 1443-1466. DOI:10.1175/JAS3898.1 |
Davis C A, Galarneau T J. 2009. The vertical structure of mesoscale convective vortices[J]. Journal of the Atmospheric Sciences, 66(3): 686-704. DOI:10.1175/2008JAS2819.1 |
Davis C A, Trier S B. 2002. Cloud-resolving simulations of mesoscale vortex intensification and its effect on a serial mesoscale convective system[J]. Monthly Weather Review, 130(12): 2839-2858. DOI:10.1175/1520-0493(2002)130<2839:CRSOMV>2.0.CO;2 |
Dimego G J, Bosart L F. 1982. The transformation of tropical storm agnes into an extratropical cyclone, Part Ⅱ: moisture, vorticity and kinetic-energy budgets[J]. Monthly Weather Review, 110(5): 412-433. DOI:10.1175/1520-0493(1982)110<0412:TTOTSA>2.0.CO;2 |
Ding Y H, Liu Y Z. 1986. Study on the kinetic-energy budget of a typhoon-budgets of kinetic-energy in general flow and eddy kinetic-energy[J]. Scientia Sinica Series B-Chemical Biological Agricultural Medical & Earth Sciences, 29(2): 187-200. |
Dixon M A, Thorpe A J, Browning K A. 2003. Layer-wise attribution of vertical motion and the influence of potential-vorticity anomalies on synoptic development[J]. Quarterly Journal of the Royal Meteorological Society, 129(591): 1761-1778. DOI:10.1256/qj.02.83 |
Edmon H J. 1978. Re-examination of limited-area available potential-energy budget equations[J]. Journal of the Atmospheric Sciences, 35(9): 1655-1659. DOI:10.1175/1520-0469(1978)035<1655:AROLAA>2.0.CO;2 |
Fritsch J M, Murphy J D, Kain J S. 1994. Warm-core vortex amplification over land[J]. Journal of the Atmospheric Sciences, 51(13): 1780-1807. DOI:10.1175/1520-0469(1994)051<1780:WCVAOL>2.0.CO;2 |
Fu S, Sun J, Zhao S, et al. 2011. The energy budget of a southwest vortex with heavy rainfall over south china[J]. Advances in Atmospheric Sciences, 28(3): 709-724. DOI:10.1007/s00376-010-0026-z |
Gray S L, Dacre H F. 2006. Classifying dynamical forcing mechanisms using a climatology of extratropical cyclones[J]. Quarterly Journal of the Royal Meteorological Society, 132(617): 1119-1137. DOI:10.1256/qj.05.69 |
Hirschberg P, Fritsch J. 1991. Tropopause undulations and the development of extratropical cyclones: Diagnostic-analysis and conceptual-model[J]. Monthly Weather Review, 119(2): 518-550. DOI:10.1175/1520-0493(1991)119<0518:TUATDO>2.0.CO;2 |
James E P, Johnson R H. 2010. A climatology of midlatitude mesoscale convective vortices in the rapid update cycle[J]. Monthly Weather Review, 138(5): 1940-1956. DOI:10.1175/2009MWR3208.1 |
Lai H W, Davis C A, Jou B J. 2011. A subtropical oceanic mesoscale convective vortex observed during SoWMEX/TiMREX[J]. Monthly Weather Review, 139(8): 2367-2385. DOI:10.1175/2010MWR3411.1 |
Li N, Ran L K, Gao S T. 2016. The impact of deformation on vortex development in a baroclinic moist atmosphere[J]. Advances in Atmospheric Sciences, 33(2): 233-246. DOI:10.1007/s00376-015-5082-y |
Nicholls M E, Pielke R A Sr, Wheeler D, et al. 2018. A numerical modelling investigation of the role of diabatic heating and cooling in the development of a mid-level vortex prior to tropical cyclogenesis, Part Ⅰ: The response to stratiform components of diabatic forcing[J]. Atmospheric Chemistry and Physics, 18(19): 14393-14416. DOI:10.5194/acp-18-14393-2018 |
Pauley P, Nieman S. 1992. A comparison of quasi-geostrophic and nonquasigeostrophic vertical motions for a model-simulated rapidly intensifying marine extratropical cyclone[J]. Monthly Weather Review, 120(7): 1108-1134. DOI:10.1175/1520-0493(1992)120<1108:ACOQAN>2.0.CO;2 |
Raisanen J. 1995. Factors affecting synoptic-scale vertical motions-a statistical study using a generalized omega-equation[J]. Monthly Weather Review, 123(8): 2447-2460. DOI:10.1175/1520-0493(1995)123<2447:FASSVM>2.0.CO;2 |
Rantanen M, Raisanen J, Lento J, et al. 2017. Software for solving a generalised omega equation and the Zwack-Okossi height tendency equation using WRF model output[J]. Geoscientific Model Development, 10(2): 827-841. DOI:10.5194/gmd-10-827-2017 |
Raymond D J, Jiang H. 1990. A theory for long-lived mesoscale convective systems[J]. Journal of the Atmospheric Sciences, 47(24): 3067-3077. DOI:10.1175/1520-0469(1990)047<3067:ATFLLM>2.0.CO;2 |
Rier S B, Davis C A. 2002. Influence of balanced motions on heavy precipitation within a long-lived convectively generated vortex[J]. Monthly Weather Review, 130(4): 877-899. DOI:10.1175/1520-0493(2002)130<0877:IOBMOH>2.0.CO;2 |
Strahl J L, Smith P J. 2001. A diagnostic study of an explosively developing extratropical cyclone and an associated 500-hPa trough merger[J]. Monthly Weather Review, 129(9): 2310-2328. DOI:10.1175/1520-0493(2001)129<2310:ADSOAE>2.0.CO;2 |
Tarbell T, Warner T, Anthes R. 1982. An example of the initialization of the divergent wind component in a mesoscale numerical weather prediction model[J]. Monthly Weather Review, 109(1): 77-95. DOI:10.1175/1520-0493(1981)1092.0.CO;2 |
Trier S B, Davis C A. 2007. Mesoscale convective vortices observed during BAMEX Part Ⅱ: Influences on secondary deep convection[J]. Monthly Weather Review, 135(6): 2051-2075. DOI:10.1175/MWR3399.1 |
Weisman M L, Davis C A. 1998. Mechanisms for the generation of mesoscale vortices within quasi-linear convective systems[J]. Journal of the Atmospheric Sciences, 55(16): 2603-2622. DOI:10.1175/1520-0469(1998)055<2603:MFTGOM>2.0.CO;2 |
Wu G, Liu H. 1998. Vertical vorticity development owing to down-sliding at slantwise isentropic surface[J]. Dyn.Atmos.Ocean, 27(1-4): 715-743. DOI:10.1016/S0377-0265(97)00040-7 |
Xu Q, Cao J. 2012. Semibalance Model in Terrain-Following Coordinates[J]. Journal of the Atmospheric Sciences, 69(7): 2201-2206. DOI:10.1175/JAS-D-12-012.1 |
Xu Q, Wei L, Jin Y, et al. 2015. A dynamically constrained method for determining the vortex centers of tropical cyclones predicted by high-resolution models[J]. Journal of the Atmospheric Sciences, 72(1): 88-103. DOI:10.1175/JAS-D-14-0090.1 |
Yang S, Zuo Q, Gao S. 2017. Image of local energy anomaly during a heavy rainfall event[J]. Chinese Physics B, 26(11): 412-433. |
Yu C K, Jou B J D, Smull B F. 1999. Formative stage of a long-lived mesoscale vortex observed by airborne Doppler radar[J]. Monthly Weather Review, 127(5): 838-857. DOI:10.1175/1520-0493(1999)127<0838:FSOALL>2.0.CO;2 |
Zhang D L. 1992. The formation of a cooling-induced mesovortex in the trailing stratiform region of a midlatitude squall line[J]. Monthly Weather Review, 120(12): 2763-278. DOI:10.1175/1520-0493(1992)120<2763:TFOACI>2.0.CO;2 |
Zhang D L, Fritsch J M. 1988. Numerical-simulation of the meso-beta scale structure and evolution of the 1977 johnstown flood Part3 internal gravity-waves and the squall line[J]. Journal of the Atmospheric Sciences, 45(7): 1252-1268. DOI:10.1175/1520-0469(1988)045<1252:NSOTMS>2.0.CO;2 |
 2019, Vol. 38
2019, Vol. 38 
