引言

集合预报是基于大气混沌理论发展而来的，20世纪80年代以来，集合预报的理论研究和实际应用均处于不断的发展中，为解决单一的确定性预报存在的不确定性问题提供了一条可靠的科学途径。在集合预报中，通常会通过一定的初值扰动方法估计模式初值的误差分布并获得一组初值的集合，并通过一定的物理过程扰动方法和侧边界扰动方法体现出数值模式中物理过程和侧边界的不确定性，在此基础上进行数值积分获得一组预报集合，由此推断大气运动的所有可能状态。21世纪以来，集合预报的理论研究越来越成熟(杜钧和陈静, 2010a, 2010b；杜钧和邓国，2010；杜钧和李俊，2014；张涵斌等，2017；Buizza et al., 2005；Bowler et al., 2008)，业务应用也越来越普遍(李俊等，2010；彭涛等，2010；王智等，2018；朱鹏飞等，2015; 李淑娟等，2018)，目前已成为日常天气预报业务中的重要工具。

THORPEX(The Observing System Research and Predictability Experiment)是世界气象组织建立的一个10 a的研究和发展计划，主要开展观测系统研究与可预报性试验。TIGGE (THORPEX Interactive Grand Global Ensemble, 全球交互式大集合)项目(智协飞和陈雯，2010)是THORPEX的一个重要组成部分，该项目的实施将全球十多个数值预报中心的集合预报产品集中起来，并建立了3个TIGGE集合预报产品数据库中心，用户可通过网络获取需要的集合预报资料。TIGGE技术实现以后，许多学者就如何充分利用各个数值预报中心的多模式集合预报资料提高预报准确率开展了较多的研究(李佰平和智协飞，2012；林春泽等，2009；智协飞等, 2009, 2013)。另外，对不同数值预报中心的集合预报在某个特定区域的预报效果检验评估工作也有较多的文献报道(皇甫雪官，2002；陈纾杨等，2013；陈博宇等，2015；张华龙等，2017; 李曼等，2018)，绝大多数检验结果均表明：集合预报产品的使用能够在一定程度上反映出预报的不确定性，相对于单一的确定性预报有一定的优势，能够给预报员提供更多有用的信息。

我国西南地区地形复杂，既受到青藏高原大地形的影响，也受到秦岭、大巴山等中小尺度复杂地形的影响，影响该地区的天气系统也复杂多变，预报不确定性较大，近年来，预报业务人员对集合预报产品的应用越来越普遍。欧洲中期天气预报中心全球集合预报(以下简称EC_GEPS)和美国国家大气环境预报中心全球集合预报(以下简称NCEP_GEPS)是TIGGE的子集，目前在国内气象预报业务(短临预报、中期预报、延伸期预报以及空气污染潜势预报等)中得到了广泛的应用，但目前对EC_GEPS和NCEP_GEPS在西南地区复杂地形下地面要素预报性能进行详细评估的工作尚不多见，本文拟对EC_GEPS和NCEP_GEPS在西南地区复杂地形下的地面要素预报结果进行详细地检验评估，对比两套集合预报系统预报性能的差异，分析两套集合预报系统误差的分布特征，以期为预报员合理使用上述集合预报产品提供一定的参考。

1 资料和方法

本文基于EC_GEPS(包括控制预报和50个集合成员)和NCEP_GEPS(包括控制预报和20个集合成员)的2016年1月1日至2017年12月31日连续2 a逐日08时(北京时，下同)起报的集合预报资料，对两套系统在西南地区(西藏、云南、贵州、四川和重庆)10 d以内的预报员应用较多且重点关注的2 m温度和24 h累计降水的定量降水预报进行检验评估和综合分析。检验针对该区域的437个国家基本站(西藏39站、云南125站、贵州84站、四川154站、重庆35站)进行，将模式预报资料通过双线性插值方法匹配到观测站点进行统计检验。本文所有的结果均为2016年1月1日至2017年12月31日时段内平均的检验结果，后文不再赘述。

2 m温度是一个连续性变量，具体的检验方案主要包括以下几方面：通过对比控制预报和集合平均(本文的集合平均是指集合成员的算术平均，下同)的均方根误差了解集合平均是否相对于控制预报有明显的改进效果；通过对比集合平均的均方根误差和集合离散度了解集合预报的离散度适宜性，即“离散度-误差关系”检验；通过计算Talagrand分布了解集合成员的等同性情况以及集合预报误差分布特征；通过计算Outlier评分了解实况落在集合成员构成的预报值区间之外的概率(即预报失误概率)；通过计算由集合成员构成的不同集合百分位、集合最小值、集合最大值预报的均方根误差了解不同集合百分位预报性能的差异以及是否存在明显的最优预报。

24 h累计降水预报的具体检验方案主要包括以下几方面：通过计算Talagrand分布了解集合成员的等同性情况以及集合预报误差分布特征；通过计算Outlier评分了解实况落在集合成员构成的预报值区间之外的概率(即预报失误概率)；通过计算相对作用特征面积评分对比分析两套系统的降水概率预报技巧；对比分析由集合成员构成的不同集合百分位、集合最小值、集合最大值的预报性能以及是否存在明显的最优预报，由于青藏高原地区观测站点稀疏、降水的气候分布也与检验区域内的其他地区差异较大，为了保证检验的公平性以及得到更加准确的结论，本文采用概率空间中的稳定公平误差评分(SEEPS, Stable Equitable Error in Probability Space)来评估不同集合百分位的降水预报性能，目前该方法已得到国际上的认可及普遍应用，该方法能够有效的克服传统的降水评分方法(TS评分等)存在的几个缺陷和不足，且最终得到的是一个单一的降水预报技巧评分，便于进行对比分析。

具体的检验方法及计算公式(李俊等，2010；陈良吕等，2017；杜钧，2002；Rodwell et al., 2010；陈法敬和陈静，2015)如下：

(1) 集合离散度：集合离散度S(t)表示集合预报相对于参考场的不确定性，具体计算公式如下

$ S(t) = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^N {{{\left({{f_i}(t) - {f_0}{{(t)}_i}} \right)}^2}} } $

其中t为预报时效，f_i(t)为扰动预报(i = 1, 2......... N)，f₀(t)为集合预报的平均。通常认为一个可靠的集合预报系统，其集合成员的离散度应该和集合平均的预报误差相当，一个理想的集合预报系统中，离散度与预报误差之间应有正比例关系，即满足所谓“离散度-误差关系”。离散度太小，则“真值”被漏掉的概率大，预报系统的可靠性差，反之则集合预报系统设计不够集约。

(2) Talagrand分布：用于检验一个集合预报系统的概率分布，即检验成员等同性和离散度情况，其思想是观测值或分析值应该以同样概率落在一个好的EPS各预报成员附近。做法是把N个集合预报成员按照升序排列，得到N + 1个区间，分别计算每个格点上N + 1个区间内分析(或观测)发生的次数，取总样本平均得到N + 1个区间上预报正确的概率，画出柱状图即为Talagrand分布。一个理想集合预报系统的Talagrand分布应该是平直的，即实况落在由集合成员预报值按从小到大排列所形成的各个等级区间的概率相同，因此，通过不同的Talagrand分布型，也可以分析出集合预报系统的系统性偏差。

(3) 预报失误概率Outlier评分：在Talagrand分布中，将分析(观测)落在预报值区间之外的平均概率称为预报失误概率，其值越大，说明预报失误的概率越大，它是对Talagrand分布的有益补充，一个具有n个成员的理想集合预报系统，其实况落在集合预报区间之外的概率为2/(n+1)。

(4) 集合百分位、集合最小和最大预报：将每个个点上N个集合成员从小到大排列，相应的，排列序号为1的预报称为集合最小预报，排列序号为N的预报称为集合最大预报，排列序号为m对应的预报称为百分之(100×m/N)集合百分位预报。集合百分位预报是一种常用的集合预报产品，能够给用户提供很多有价值的信息。

(5) 相对作用特征(ROC)曲线及其面积(AROC)：表示预报区分事件发生和不发生的能力，把1分为K个概率区间(如0~0.1，0.1~0.2，等)，每个分位数所对应的命中率相对于空报率的变化曲线称为ROC曲线，曲线越靠近命中率，则预报越好；曲线下的面积称为ROC面积，可作为ROC曲线的技巧评分，ROC面积取值范围0~1，越大越好，1为理想值，0.5以下为无技巧值。

(6) SEEP技巧评分：该方法首先利用降水气候概率概率空间中把降水分为“干”、“小雨”和“大雨”三类，“小雨”概率为“大雨”概率的两倍。SEEPS将降水检验评分定义为两个矩阵的标量积：一个3×3列联表矩阵，为降水预报和观测的二维离散概率分布，代表了概率空间中的降水预报特征；另一个为基于降水概率的3×3的误差评分矩阵，代表了在一定的降水概率下SEEPS评分对概率空间中不同预报误差的“惩罚”。在此基础上，对不同站点赋予与站点密度成反相关的权重并计算区域平均的检验评分。SEEPS是一种误差评分，值域期望为[0, 1]，在实际应用中通常使用与之相应的SEEPS技巧评分1-SEEPS，值域期望为[0, 1]，1代表“完美预报”。

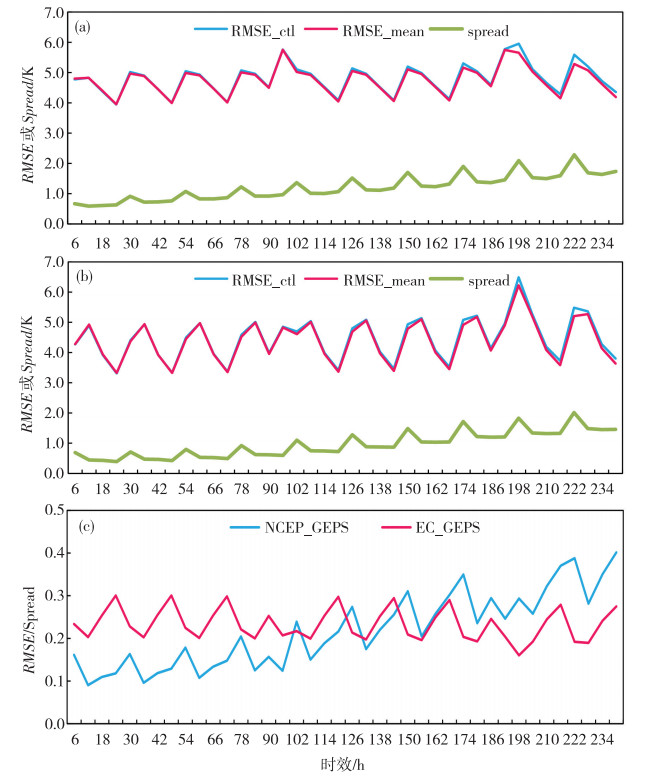
2 2 m温度检验

图 1是EC_GEPS和NCEP_GEPS的2 m温度6—240 h逐6 h控制预报和集合平均的均方根误差及集合离散度, 从图中可以看出：EC_GEPS各个预报时效的2 m温度控制预报和集合平均的均方根误差总体介于4.08~5.75 K之间，集合离散度总体介于0.59~2.28 K之间；NCEP_GEPS各个预报时效的2 m温度控制预报和集合平均的均方根误差总体介于3.32~6.62 K之间，集合离散度总体介于0.39~2.01 K之间；总体而言，两套系统控制预报和集合平均预报的误差均普遍偏高，除个别预报时效外，NCEP_GEPS的预报误差低于EC_GEPS；EC_GEPS和NCEP_GEPS的上述检验量随预报时效变化的特征基本一致，均呈现出较为明显的日变化特征，即08—14时(北京时，下同)明显增大，14时—次日08时逐渐减小，这是2 m温度误差检验中普遍存在的情况；2 m温度预报的集合平均均方根误差与控制预报均方根误差基本相当，在较长预报时效上(120—240 h)略有正效果；各个预报时效的集合离散度均明显低于集合平均的均方根误差, 图 1c为两套系统各个预报时效集合离散度与集合平均均方根误差的比(SPD-ERR)，该比值介于0~1之间，越大越好，1为完美值，从图中可见：EC_GEPS的SPD-ERR总体介于0.20~0.30之间；NCEP_GEPS的SPD-ERR总体介于0.09~0.40之间；EC_GEPS的SPD-ERR在6—144 h预报时效内明显高于NCEP_GEPS，此后的150—240 h预报时效内明显高于NCEP_GEPS。

图 2给出了EC_GEPS和NCEP_GEPS的2 m温度部分预报时效的Talagrand分布，从图中可以看出：EC_GEPS和NCEP_GEPS不同预报时效2 m温度的Talagrand分布均呈现出了非常明显的“J型”分布特征，其余预报时效也表现出了同样的特征(因篇幅有限，图略)，说明实况2 m温度高于各集合成员预报值的概率较大，集合预报系统在2 m温度的预报上存在偏低的系统性误差。

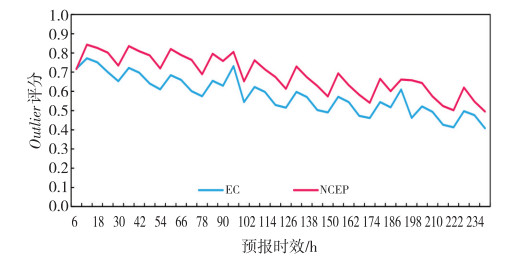
图 3是EC_GEPS和NCEP_GEPS的2 m温度6—240 h逐6 h的Outlier评分, 从图中可以看出：EC_GEPS和NCEP_GEPS的2 m温度不同预报时效的Outlier评分均普遍偏高，且随着预报时效的延长总体表现出逐渐减小的趋势，这也与图 1中两者的集合离散度随预报时效延长而增大的趋势一致。EC_GEPS的Outlier评分总体介于0.41~0.77之间，NCEP_GEPS的Outlier评分总体介于0.49~0.84之间；EC_GEPS在各个预报时效的Outlier评分均明显低于NCEP_GEPS的Outlier评分，说明EC_GEPS的预报失误概率相对较低。

图 4给出了EC_GEPS和NCEP_GEPS的2 m温度6—240 h逐6 h不同集合百分位预报的均方根误差(因篇幅有限，图中略去了部分集合百分位的均方根误差分布曲线)，图中min表示集合最小值预报，max表示集合最大值预报，f10，f30，f50，f70，f90分别表示相应的集合百分位预报，从图中可以看出：EC_GEPS和NCEP_GEPS的不同集合百分位2 m温度预报的均方根误差随预报时效演变的特征基本一致，均呈现出较为明显的日变化特征，即08—14时明显增大，14时—次日08时逐渐减小，随着集合百分位的增大，各个预报时效的均方根误差逐渐减小，集合最大值的均方根误差最低，这与图 2中2 m温度的Talagrand呈J型分布的特征一致；另外，集合最大值的均方根误差除个别预报时效外均低于控制预报和集合平均预报的均方根误差(图略)，这与两者2 m温度预报存在系统性偏低有关(见图 2)。

3 24 h累计降水检验

图 5是EC_GEPS和NCEP_GEPS不同预报时效的24 h累计降水预报(因篇幅有限，其余累计降水预报时段的Talagrand分布图略)的Talagrand分布, 从图中可以看出：EC_GEPS的192 h、216 h和240 h的Talagrand分布较为理想，其余预报时效均在一定程度上呈现出了一定的“L型”分布；NCEP_GEPS各个预报时效的Talagrand分布均一呈现出了非常明显的“L型”分布。Talagrand分布呈现出“L型”分布特征说明集合成员的预报整体高于实况的概率较大，说明集合预报系统的定量降水预报在一定程度上存在着预报偏大的系统性误差。

图 6是EC_GEPS和NCEP_GEPS的24—240 h逐24 h累计降水的Outlier评分, 从图中可以看出：EC_GEPS和NCEP_GEPS的24 h累计降水Outlier评分随着预报时效的延长总体表现出逐渐减小的趋势，这可能与降水预报的离散度随预报时效的延长而增大有关；EC_GEPS的Outlier评分总体介于0.1~0.3之间，NCEP_GEPS的Outlier评分普遍偏高，总体介于0.34~0.54之间；EC_GEPS在各个预报时效的Outlier评分均明显低于NCEP_GEPS的Outlier评分，说明EC_GEPS的预报失误概率相对较低，实况更多地被包含在集合区间之内。

图 7是EC_GEPS和NCEP_GEPS各个降水量级24—240 h逐24 h累计降水的AROC评分, 从图中可以看出：对于小雨、中雨和大雨量级各个预报时效的AROC评分，EC_GEPS明显优于NCEP_GEPS；对于暴雨和大暴雨量级各个预报时效的AROC评分，EC_GEPS和NCEP_GEPS基本相当；EC_GEPS和NCEP_GEPS仅暴雨和大暴雨量级的个别预报时效的AROC评分低于无技巧值0.5，说明两套系统总体而言能够对各个量级降水提供有价值的概率预报信息。

图 8给出了EC_GEPS和NCEP_GEPS的24—240 h逐24 h累计降水不同集合百分位预报的SEEPS技巧评分(因篇幅有限，图中略去了部分集合百分位的SEEPS技巧评分分布曲线), 图中min表示集合最小值预报，max表示集合最大值预报，f10，f20，f30，f40，f50，f60，f70，f80，f90分别表示相应的集合百分位预报，从图中可以看出：EC_GEPS从集合最小值到70%集合百分位，随着集合百分位增大，各个预报时效的SEEPS技巧评分表现出逐渐增大的趋势。从70%集合百分位到集合最大值，随着集合百分位的增大，各个预报时效的SEEPS技巧评分表现出逐渐减小的趋势。70%集合百分位具有最高的预报技巧且优于控制预报和集合平均预报；NCEP_GEPS也表现出类似的特征，从集合最小值到80%集合百分位，随着集合百分位的增大，各个预报时效的SEEPS技巧评分表现出逐渐增大的趋势。从80%集合百分位到集合最大值，随着集合百分位的增大，各个预报时效的SEEPS技巧评分表现出了逐渐减小的趋势。80%集合百分位具有最高的预报技巧且优于控制预报和集合平均预报。

4 结论和讨论

本文基于TIGGE中EC_GEPS和NCEP_GEPS的2016年1月1日至2017年12月31日连续2 a的集合预报资料，对两套系统在西南地区10 d以内的2 m温度和24 h累计降水定量降水预报进行检验评估，对比分析了两套集合预报系统集合预报性能的差异及预报误差的分布特征，检验结果及讨论如下：

(1) EC_GEPS和NCEP_GEPS在西南地区10 d以内2 m温度的控制预报和集合平均的均方根误差均普遍偏高，NCEP_GEPS预报总体而言优于EC_GEPS。

(2) EC_GEPS和NCEP_GEPS的2 m温度集合平均预报均方根误差与控制预报均方根误差基本相当，较长预报时效(120—240 h)略有改进；集合离散度均明显低于集合平均的均方根误差，表明系统的离散度偏小；集合成员的算术平均能够在一定程度上消除模式预报的随机性误差，因此集合平均的误差评分通常而言都优于控制预报的误差评分，但理论上集合成员具有与控制预报一致的所有系统性误差，因此集合平均不能有效地消除模式预报的系统性误差。结合Talagrand分布的分析可知，两套集合预报系统在西南地区的2 m温度预报均存在非常明显的系统性误差，因此也能在一定程度上说明预报误差中系统性误差所占的比例较大而随机性误差所占的比例较小。因此，集合平均均方根误差相对于控制预报的改进效果不明显。

(3) EC_GEPS和NCEP_GEPS的2 m温度预报的Talagrand分布总体而言均呈现出了非常明显的“J型”分布特征，Outlier评分均普遍偏高且EC_GEPS的Outlier评分明显低于NCEP_GEPS，由此说明两套系统均存在着较为明显的预报偏低(冷)的系统性误差，这是造成两套系统集合平均预报相对于控制预报改进效果不明显的主要原因，也是造成系统集合离散度偏低的原因之一。

(4) EC_GEPS和NCEP_GEPS的2 m温度预报从集合最小值到集合最大值，随着集合百分位的增大，各个预报时效的均方根误差逐渐减小，集合最大值的均方根误差最低且低于控制预报和集合平均预报的均方根误差。这与两套系统均存在明显的预报偏低(冷)的系统性误差相对应。

(5) 24 h累计降水检验结果表明：EC_GEPS和NCEP_GEPS的24 h累计降水定量降水预报的Talagrand分布总体而言均呈现出“L型”分布特征且NCEP_GEPS更加明显。NCEP_GEPS各个预报时效的Outlier评分均普遍偏高且明显高于EC_GEPS，表明NCEP_GEPS集合预报失误概率更大。上述结果表明EC_GEPS和NCEP_GEPS在西南地区的24 h累计降水定量降水预报均存在着一定的预报偏大的系统性误差且NCEP_GEPS更加明显。

(6) EC_GEPS的小雨、中雨和大雨量级各个预报时效的AROC评分均明显大于NCEP_GEPS，暴雨和大暴雨量级则基本相当，表明总体而言EC_GEPS具有更高的降水概率预报技巧。EC_GEPS的70%集合百分位预报技巧最高，NCEP_GEPS的80%集合百分位预报技巧最高。

本文检验分析的时间样本足够长，检验结论在西南地区应该具有一定的普适性，但西南地区地形复杂且不同地区的地形分布特征差异较大(如青藏高原地区和川东平原地区)，因此两套系统在某一特定地区的集合预报技巧及误差分布特征可能与上述检验结论有一定的差异，需要结合特定的需求进行相应的检验分析。此外，针对两套系统对2 m温度预报存在的预报偏低的系统性误差，进行相应的集合预报系统性偏差订正和集合离散度订正(李莉等，2011；马旭林等，2015)应该能较好地改进预报技巧。对于定量降水预报偏大的系统性误差，作相应的降水集合预报系统性偏差订正(周迪等，2015；杨瑞雯等，2017；李俊等，2014；李俊等，2015)应该能较好地改进预报技巧，但不同降水量级的系统性误差还有待进行更多的诊断分析。