2. 四川省气候中心, 成都 610072
2. Climate Center of Sichuan Province, Chengdu 610072
四川省暴雨灾害频发,每年因暴雨诱发的洪涝、滑坡、山洪、泥石流等灾害,给我省农业、工业、交通、通讯以及人民生命财产等造成重大损失。如2013年全省共出现6次区域性暴雨天气过程,造成2 113.7万人次受灾,349人死亡失踪,9.8万间房屋倒塌,60.5×104 hm2农作物受灾,5.7×104 hm2绝收,直接经济损失达429.6亿元[1],占当年GDP(国内生产总值)的1.64%。其中7月7-13日,汶川、芦山地震灾区出现历史罕见的区域性暴雨天气,都江堰24 h降水量达423.8 mm,过程降水量达746.4 mm,均打破历史记录,强降水引发中兴镇三溪村发生大面积山体崩塌,导致11户村民的房屋被毁,造成当地村民和游客21人死亡,108人失踪。因此,加强暴雨灾害的预评估,在灾前对其可能造成的损失做出科学估算,对于政府进行防灾减灾决策、减轻灾害损失具有重要作用。
暴雨灾害损失评估目前已成为研究热点,并在暴雨综合强度评估和灾害级别(受灾程度)评估方面取得了较大进展。王莉萍等[2]以降水强度、覆盖范围、持续时间3个指标,建立了中国4个暴雨灾害敏感区的降水过程综合强度评估模型和等级划分标准。邹燕等[3]选取最大日降水量、最大过程降水量、暴雨范围和暴雨持续时间4项指标,采用百分位数法和相关系数法,构建了福建省区域性暴雨过程的综合强度评估模型及综合强度等级划分标准。韩秀君等[4]根据平均降水量、降水强度极值和覆盖范围大小,建立了辽宁省暴雨灾害综合评估指标。蔡新玲等[5]采用等权重法构建了陕西省区域性暴雨过程综合评估指数,并利用重现期和百分位2种方法确定暴雨综合指数强度阈值。黄治勇等[6]通过分析历史暴雨个例之间灾害损失的相似性,采用类比法,建立了湖北省暴雨灾害损失定量预估模型。陈亚宁等[7]、刘伟东等[8]根据暴雨灾害造成的受灾面积、直接经济损失、受灾人口等社会经济指标,应用灰色关联度方法,进行灾度等级划分和灾情损失比较。杨帅等[9]、王秀荣等[10]综合考虑暴雨致灾因子危险性和孕灾环境脆弱性,运用加权求和方法,结合GIS技术,建立了湖南省和北京市暴雨灾害损失评估方法。袭祝香等[11]采用灰色关联度方法,研究建立了基于重大暴雨过程指数和前7 d降水量的吉林省重大暴雨过程损失评估模型。史瑞琴等[12]探讨了基于暴雨洪涝淹没模型的暴雨洪涝灾害损失评估技术。谢五三等[13]利用淹没模型研究了大通河流域的暴雨洪涝灾害风险评估方法。
已有研究成果多是针对区域性暴雨总体强度的评价和损失总量的评估,而针对单站暴雨过程的强度及其造成损失的评估则很少。目前四川尚未建立单站暴雨过程综合强度与灾害损失评估模型,鉴于暴雨灾害损失与暴雨强度、地理环境和社会经济发展水平之间的复杂关系,因此也无法借用其他地区的研究成果。本文基于历史灾情数据首先建立单站暴雨过程综合强度指数及等级划分标准,在此基础上,研究建立适合四川分县暴雨灾害损失评估的模型和方法,以期为开展暴雨过程强度和灾害损失空间分布预评估业务提供技术支撑。
1 资料与方法 1.1 资料来源气象资料来源于四川省气象探测数据中心,包括全省156个国家级气候观测站(含国家基准站、基本站和一般站) 5-10月逐日降水观测资料,由于部分台站始建于20世纪50年代末60年代初,因此为保证资料完整性,选择气象资料的时间段为1961-2015年。灾情数据来源于民政、救灾、防汛等部门的灾情普查资料和文献[14],各区县GDP、人口、农作物种植面积等社会经济资料来源于《四川省统计年鉴》。由于只收集到1999年、2000年和2013年的《四川省统计年鉴》,故本文利用2013年的资料建立评估模型,以1999年和2000年的资料对模型进行检验。
1.2 研究方法 1.2.1 暴雨综合强度指数从地理特征上四川可分为盆地、高原、山地3种类型,不同类型地区的气候和降水特征各异。将每个站点的历年最大日降水量由大到小排序并取其98百分位值,并以此计算每个区域全部台站的平均值,结果为盆地52 mm、高原23 mm、山地49 mm,这与现行业务中使用的暴雨阈值相近。为保持与现行业务标准一致,本文暴雨阈值(Rf)采用表 1所列数值,当某站日降水量大于等于Rf时,即认为该站出现1个暴雨日。
关于单站暴雨过程的定义目前尚无标准可依,本文将单站暴雨过程定义为:日降水量连续大于等于5 mm且其间至少出现1个暴雨日的强降水过程。5 mm最小日降水量指标的设定是为了既能去除暴雨日前后的绵绵细雨同时又能最大限度地保全连续降水总量,当最小日降水量阈值取5 mm时,只有0.1%的暴雨过程的持续时间超过10 d,且有60%的暴雨过程降水量占到全部连续雨日降水总量的95%以上,较好地达到了上述目的。
暴雨综合强度指数I由如下3个指标经加权求和而得,归一化过程降水量指标(Ia):
| $ {I_{\rm{a}}} = \frac{{\sum\limits_{i = 1}^d {{R_i}} }}{{{P_{\rm{m}}}}} $ | (1) |
式(1)中,Ri为某日降水量,d为日降水量大于等于5 mm的天数,Pm为该站所在区域的上限过程降水量,取该区域所有台站1961-2015年各次暴雨过程的过程降水量由小到大序列的99.9百分位值附近的整10数值,各区Pm值见表 1。当Ia大于1时,Ia取1。
|
|
表 1 各区域暴雨阈值及指标上限值 Table 1 The rainstorm determination threshold and the upper limit of each index in different regions. |
归一化最大日降水量指标(Ib):
| $ {I_{\rm{b}}} = \frac{{{R_0}}}{{{P_{\rm{m}}}}} $ | (2) |
式(2)中,R0为暴雨过程的最大日降水量,Rm为该站所在区域的上限日降水量,取该区域所有台站1961-2015年各次暴雨过程最大日降水量由小到大序列的99.9百分位值附近的整10数值,各区Rm值见表 1。当Ib大于1时,Ib取1。
归一化持续天数指标(Ic):
| $ {I_{\rm{c}}} = \frac{D}{{{D_{\rm{m}}}}} $ | (3) |
式(3)中,D为暴雨过程持续天数,定义为第1个暴雨日与最后1个暴雨日之间的天数,当只有1个暴雨日时D=1,Dm为该站所在区域的上限持续天数,取该区域所有台站1961-2015年各次暴雨过程持续天数由小到大序列的99.9百分位值的整数值,各区Dm值见表 1。当Ic大于1时,Ic取1。
暴雨综合强度指数(I)由下式计算:
| $ I = A \times {I_{\rm{a}}} + B \times {I_{\rm{b}}} + C \times {I_{\rm{c}}} $ | (4) |
式(4)中,A、B、C为权重系数,由各指标与灾情损失之间的相关系数经归一化处理而得。
根据对1961年以来全省2万多次暴雨过程的统计,91%的暴雨过程均只有1 d时间,98.8%的暴雨过程持续时间均在3 d以内,因此本文不再区分不同时长的暴雨过程。
1.2.2 灰色关联度分析与传统的多因素分析方法相比,灰色关联度分析法对数据要求较低且计算量较小,因此该方法在灾情评估领域得到了较好应用[15-16]。本文根据受灾人口占总人口的百分比(人口受灾率Pd)、直接经济损失占GDP的百分比(经济损失率Ed)、农作物受灾面积占耕地面积百分比(作物受灾率Sd) 3项灾损指标,采用灰色关联分析方法计算各次灾害的灾损灰色关联度α (以下简称灾损关联度),并据此进行灾度(受灾程度)等级G评定。为减小人为因素对灾情损失数据的干扰,在关联分析之前对灾情指标作归一化处理。根据灾情数据记录的损失分布状况,以特大灾害所占比例小于10%为标准设定损失上限,由此得到人口受灾率Pd、经济损失率Ed、作物受灾率Sd的上限分别为50%、5%、50%,当某次灾害损失超过这个上限时就认定为特大灾害。将各次灾害的3个灾情指标分别除以其上限值得到新的灾情指标序列,对新序列中大于1的值取1,由此得到归一化的灾情指标序列。
设定参考序列,计算各指标转换序列和参考序列的关联系数λm(i) :
| $ {\lambda _m}(i) = \frac{1}{{1 + {\rm{ }}{\Delta _m}(i)}} $ | (5) |
式(5)中,λm(i)为第m项指标第i时刻的关联系数,
| $ \alpha (i) = \frac{1}{M}\sum\limits_{m = 1}^M {} {\lambda _m}(i) $ | (6) |
式(6)中,α(i)为全部指标第i个时刻的灰色关联度,M为选取的单项指标个数,本文M=3。
灾度等级G根据灰色关联度大小按表 2标准确定。
|
|
表 2 基于灾损关联度的灾度划分标准 Table 2 The disaster severity standard based on the correlation degree of disaster loss. |
利用前述定义的暴雨过程Ia、Ib、Ic这3项评估指标,采取同样方法,计算得到历次暴雨过程的灰色关联度β(以下简称暴雨关联度)。
2 结果分析 2.1 暴雨强度评估暴雨综合强度指数I根据归一化的过程降水量Ia、最大日降水量Ib和持续天数Ic这3项指标加权求和计算,其权重系数根据各项指标与人口受灾率Pd、经济损失率Ed和作物受灾率Sd的平均相关系数,经归一化处理后得到。表 3给出3项暴雨评估指标与3项灾损指标之间的相关系数,从中可见,经前述方法处理后的各项暴雨评估指标与灾损指标之间具有很好的相关性,相关系数在0.37~0.67之间,信度为0.01。根据表 3计算得到的Ia、Ib、Ic的权重系数分别为0.38、0.35、0.27,因此暴雨综合强度指数I的计算公式为:
| $ I = 0.38 \times {I_{\rm{a}}} + 0.35 \times {I_{\rm{b}}} + 0.27 \times {I_{\rm{c}}} $ | (7) |
|
|
表 3 暴雨评估指标与灾损指标间的相关系数 Table 3 The correlation coefficient between rainstorm assessment index and disaster loss index. |
利用(7)式计算1981-2010年气候标准期内各次暴雨过程的综合强度指数,根据其平均值
|
|
表 4 暴雨综合强度指数等级标准 Table 4 The grade standard of rainstorm comprehensive strength index. |
根据表 4标准计算得到的1961-2015年弱、中、强、极强暴雨的平均发生频率(全部台站某等级暴雨发生次数除以暴雨总次数)分别为50.7%、28.6%、12.9%、7.8%。从极强暴雨的空间分布看(图 1),盆地北部山区、西部山区和甘孜州南部易发生极强暴雨,发生频率在10%以上,极强暴雨中心位于剑阁、北川、名山、稻城等地,发生频率在15%以上,其中北川可达30%,即发生在北川的暴雨有近三分之一是极强暴雨。

|
图 1 四川极强暴雨发生频率空间分布图 Fig. 1 Spatial distribution of the frequency of extreme heavy rainstorm in Sichuan. |
利用2013年各站点暴雨和灾损资料,采用线性回归方法,建立了经济损失率、人口受灾率、作物受灾率及灾损关联度与暴雨综合强度指数、暴雨关联度之间的统计模型(表 5)。
|
|
表 5 暴雨灾损评估模型 Table 5 The assessment model of rainstorm disaster loss. |
图 2-3给出部分指标间的关系图,结合表 5分析可知,暴雨综合强度指数和暴雨关联度与各灾损评估指标之间均具有较高的相关性,相关系数在0.6~0.8之间,均通过了0.01的统计检验。从表 5还可知,各项灾损指标与暴雨关联度之间的相关系数均高于与暴雨综合强度指数之间的相关系数,说明用暴雨关联度进行灾损评估效果更好。各灾损评估指标与暴雨关联度之间相关系数的相对大小依次为α>Ed>Sd>Pd。
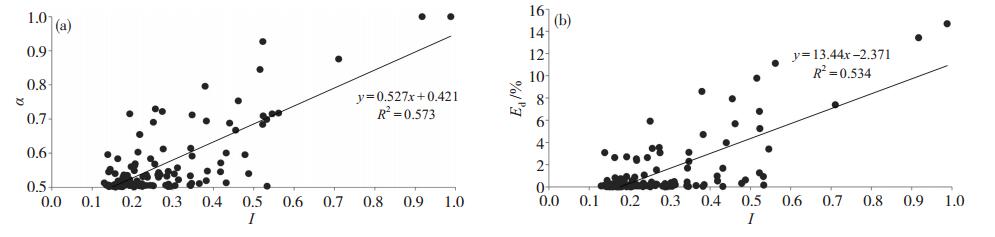
|
图 2 暴雨综合强度指数I与灾损关联度α (a)和经济损失率Ed (b)关系图 Fig. 2 The relationship between the comprehensive strength index of rainstorm and (a) the correlation degree of disaster loss and (b) the economic loss rate. |
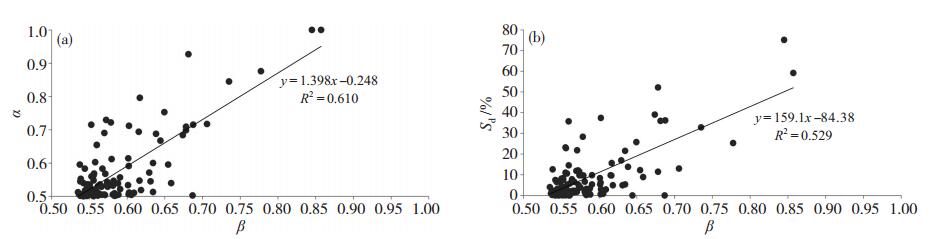
|
图 3 暴雨关联度β与灾损关联度α (a)和作物受灾率Sd (b)关系图 Fig. 3 The relationship between the grey correlation degree of rainstorm and (a) the correlation degree of disaster loss and (b) the crops affected rate. |
利用2013年暴雨灾损资料对回归模型进行误差分析(表 6)可知,评估等级与实际等级相同的比例达60%以上,相同及只差1个等级的比例达95%以上,相差2个等级的不足5%,未出现相差3个等级以上的情况;估算的经济损失率与实际经济损失率的平均绝对差小于1.5%,估算的人口受灾率与实际人口受灾率的平均绝对差约为7%,估算的作物受灾率与实际作物受灾率的平均绝对差约为6%。利用1999-2000年的暴雨灾损资料对上述模型进行检验,从回代检验结果看,评估等级与实际等级相同的比例达50%以上,相同及只差1个等级的比例达90%以上,相差2个等级的不足10%,也未出现相差3个等级以上的情况;估算的经济损率与实际经济损失率的平均绝对差小于2%,估算的人口受灾率与实际人口受灾率的平均绝对差小于12%,估算的作物受灾率与实际作物受灾率的平均绝对差小于11%。
|
|
表 6 灾损评估模型精度检验结果 Table 6 The accuracy test result of disaster loss assessment model. |
由于目前尚未见到关于单站暴雨灾损评估的相关研究,所以选择区域性暴雨的灾损评估案例进行比较,以检验本文的暴雨灾损评估精度。根据文献[11]对吉林省54次区域性暴雨过程灾度等级的评估可知,拟合灾度等级与实际灾度等级同级及只差1个等级的比例为98%,而本文基于暴雨关联度的灾度等级评估模型的这一比例为95.8%,说明本文的单站暴雨灾度评估精度与文献[11]的区域性暴雨灾度评估精度相当。
2.3 灾损风险评估利用欧洲中心数值预报结果,对2016年7月5-7日发生在盆地西部的暴雨过程强度和可能造成的灾损进行提前1 d的预评估(图略),结果表明:在盆地西北部和西南部将有37站出现暴雨,其中盆西北绵阳、德阳等地13站为强暴雨,盆西南雅安、眉山等地8站为极强暴雨,27站重现期在5 a以下,雅安附近重现期约为10 a。图 4为灾损预评估分布图,从中可见,这次暴雨过程可能造成的经济损失率大多在2%以下,人口受灾率和作物受灾率一般小于10%,多数地方的灾度等级属于微灾;盆地西南部雅安市的一些地方损失稍重,经济损失率在2%~3%,人口受灾率和作物受灾率在10%~15%,其灾度等级为小灾。据四川省民政厅报告,此次暴雨过程共造成4.2万人受灾,1人死亡,农作物受灾面积2.8千公顷,绝收600公顷,直接经济损失5900余万元,灾情损失较轻,预评估的灾度等级与实际相符。
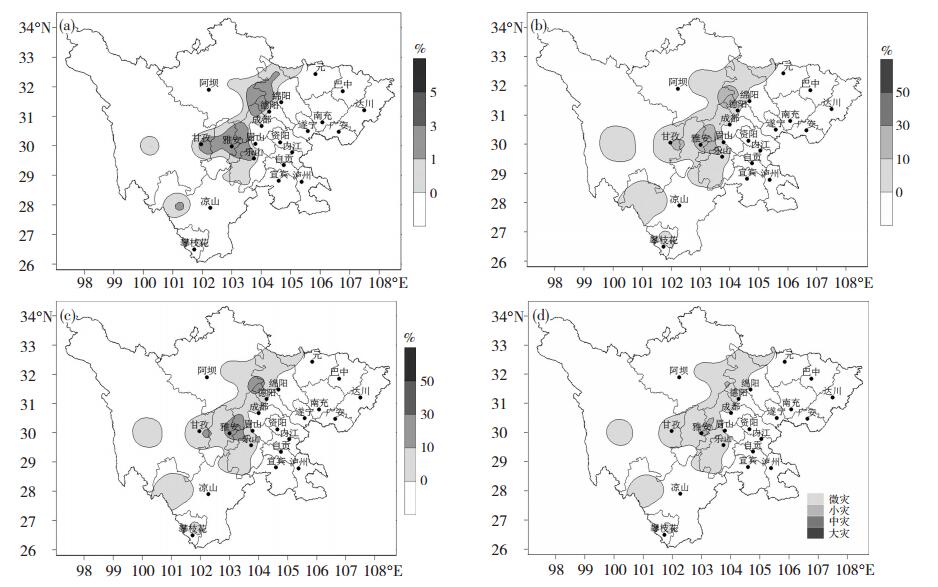
|
图 4 2016年7月5—7日暴雨过程灾损预评估分布图:(a)经济损失率,(b)人口受灾率,(c)作物受灾率,(d)灾度 Fig. 4 The distribution of predictive assessment of the rainstorm disaster from 5 to7 in July 2016: (a) the economic loss rate, (b) the population affected rate, (c) the crops affected rate, and (d) disaster degree |
利用1961-2015年逐日降水资料,根据公式(7)计算出各站点历次暴雨过程的综合强度指数I,并挑选出每年最大值,形成各站点最大暴雨强度指数序列Imax, 经柯尔莫哥洛夫拟合优度检验(K-S检验)可知,除川西高原和川西南山地的少数站点外,大部分站点的Imax序列均服从Gumbel分布。因此本文首先利用Gumbel分布函数计算出各站点5 a一遇和50 a一遇的综合强度指数Imax,然后利用表 5给出的经济损失评估模型,计算得到各站点遭受5 a一遇和50 a一遇暴雨时可能造成的经济损失率(图 5)。分析可知,对于5 a一遇的暴雨,其经济损失率一般均在2%以下,盆地北部和西部山区、甘孜州南部、攀枝花西部和凉山州南部在2%~3%之间,盆东北、盆西北和盆西南的部分地方可达3%~4%。对于50 a一遇的暴雨,其造成的经济损失率明显高于5 a一遇的暴雨,绝大部分地方的经济损失率均在3%以上,盆地北部和西部山区、甘孜州南部、攀枝花西部和凉山州南部的经济损失率在5%以上,巴中、广元、绵阳、德阳、雅安、乐山等市的部分地方可达7%~9%。
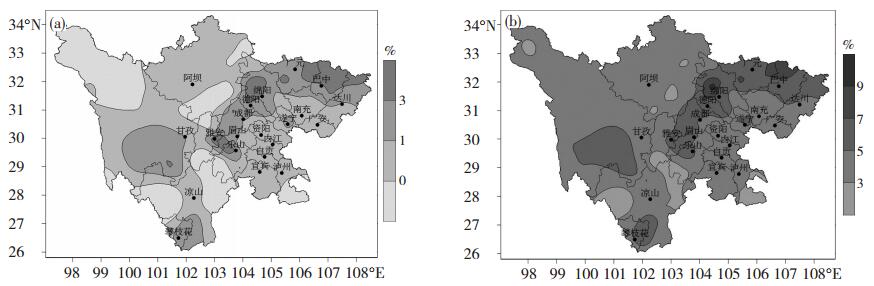
|
图 5 5 a一遇(a)和50 a一遇(b)暴雨可能造成的经济损失率分布图 Fig. 5 The distribution of economic loss rate at (a) 5-year return period and (b) 50-year return period. |
2013年6月30日-7月1日遂宁经历100 a不遇的特大暴雨,日最大降水量达415.9 mm,过程降水量达519.5 mm,均超过历史记录,暴雨造成遂宁城区出现内涝,60多个小区遭水淹,经开区33家工业企业厂房进水受损,直接经济损失12亿元,占当年GDP的13%,按本文方法估算的经济损失率为10%。2013年7月8-10日发生在都江堰的特大暴雨,其强度为100 a不遇,中兴镇发生大面积山体崩塌,造成重大人员伤亡,直接经济损失约33亿元,占当年GDP的14%,按本文方法估算的经济损失率为11%。这两次100 a不遇的暴雨过程,其估算的经济损失率与实际的经济损失率之间相差3%,说明根据本文方法估算的损失较为合理。
3 结论与讨论本文利用降水、灾情和社会经济历史资料,研究建立了四川单站暴雨综合强度及灾损评估模型,并对模型的合理性进行了检验,最后将模型应用于暴雨灾损的预评估和风险评估,得出如下结论:
(1) 四川省内盆地、高原、山地降水差异较大,以这3种类型地区的气候暴雨过程的最大日降水量、过程降水量、持续天数3个指标的上限值为基准,经归一化处理后,3个指标与经济损失率、人口受灾率、作物受灾率等灾损指标的相关关系显著。
(2) 利用基于归一化的过程降水量、最大日降水量和过程持续天数加权求和的暴雨综合强度指数及等级标准,对近55 a暴雨过程的评估结果表明,不同强度等级暴雨的时频和空间特征较为合理,暴雨综合强度指数可用于四川暴雨综合强度的预评估。
(3) 经检验,本文建立的基于暴雨综合强度指数和基于暴雨关联度的灾损评估模型,其灾度等级评估误差一般在1个级差以内,经济损失率的平均误差小于2%,人口受灾率和作物受灾率的平均误差小于10%,具有较高的准确性,可应用于暴雨灾损预评估。
(4) 基于暴雨综合强度指数的经济损失率计算结果表明,对于5 a一遇的暴雨过程,其经济损失率多在3%以下,而50 a一遇的暴雨过程,其经济损失率多在3%以上,盆地北部和西部山区在5%以上,局地可达7%~9%。
本文建立的暴雨灾损评估模型,主要考虑了暴雨自身强弱对灾损的影响,但暴雨造成的损失大小,不仅取决于暴雨致灾因子的危险程度,还与其他诸多因素密切相关,如前期降水状况、孕灾环境的敏感性、承灾体的脆弱性以及防灾减灾能力等,这些因素的影响还有待今后深入研究。
| [1] |
中国气象局. 中国气象灾害年鉴(2014)[M]. 北京: 气象出版社, 2015: 162.
|
| [2] |
王莉萍, 王秀荣, 王维国. 中国区域降水过程综合强度评估方法研究及应用[J]. 自然灾害学报, 2015, 24(2): 186-194. |
| [3] |
邹燕, 叶殿秀, 林毅, 等. 福建区域性暴雨过程综合强度定量化评估方法[J]. 应用气象学报, 2014, 25(3): 360-364. DOI:10.3969/j.issn.1001-7313.2014.03.014 |
| [4] |
韩秀君, 孙晓巍, 李爽, 等. 辽宁暴雨致灾指标及灾害影响预评估[J]. 气象与环境学报, 2014, 30(6): 80-84. |
| [5] |
蔡新玲, 路岑之, 程肖侠. 陕西省区域性暴雨过程综合评估方法研究[J]. 陕西气象, 2012(6): 16-19. DOI:10.3969/j.issn.1006-4354.2012.06.005 |
| [6] |
黄治勇, 龙利民, 邵末兰, 等. 类比法在暴雨灾害损失定量预估中的应用[J]. 大气科学学报, 2011, 34(2): 246-250. DOI:10.3969/j.issn.1674-7097.2011.02.015 |
| [7] |
陈亚宁, 杨思全. 自然灾害的灰色关联灾情评估模型及应用研究[J]. 地理科学进展, 1999, 18(2): 158-162. DOI:10.3969/j.issn.1007-6301.1999.02.009 |
| [8] |
刘伟东, 扈海波, 程丛兰, 等. 灰色关联度方法在大风和暴雨灾害损失评估中的应用[J]. 气象科技, 2007, 35(4): 563-566. DOI:10.3969/j.issn.1671-6345.2007.04.023 |
| [9] |
杨帅, 苏筠. 县域暴雨洪涝灾害损失快速评估方法探讨__以湖南省为例[J]. 自然灾害学报, 2014, 23(5): 156-153. |
| [10] |
王秀荣, 吕终亮, 王莉萍, 等. 一种简化的暴雨灾害风险及影响评估方法和应用研究-以京津冀"7.21"暴雨事件为例[J]. 气象, 2016, 42(2): 213-220. |
| [11] |
袭祝香, 纪玲玲, 张硕. 吉林省重大暴雨过程影响损失评估模型的建立[J]. 气象与环境学报, 2014, 30(5): 141-145. |
| [12] |
史瑞琴, 刘宁, 李兰, 等. 暴雨洪涝淹没模型在洪灾损失评估中的应用[J]. 暴雨灾害, 2013, 32(4): 379-384. DOI:10.3969/j.issn.1004-9045.2013.04.012 |
| [13] |
谢五三, 田红, 卢燕宇. 基于FloodArea模型的大通河流域暴雨洪涝灾害风险评估[J]. 暴雨灾害, 2015, 34(4): 384-387. DOI:10.3969/j.issn.1004-9045.2015.04.012 |
| [14] |
《中国气象灾害大典》编委会. 中国气象灾害大典:四川卷[M]. 北京: 气象出版社, 2006: 64-207.
|
| [15] |
王博, 崔春光, 彭涛, 等. 暴雨灾害风险评估与区划的研究现状与进展[J]. 暴雨灾害, 2007, 26(3): 281-286. DOI:10.3969/j.issn.1004-9045.2007.03.017 |
| [16] |
邓兴旺, 张涛, 吴涛涛. 利用数值预报产品制作府环河流域面雨量预报试验[J]. 暴雨灾害, 2008, 27(1): 68-78. DOI:10.3969/j.issn.1004-9045.2008.01.012 |
 2019, Vol. 38
2019, Vol. 38 
