引言

我国是世界上自然灾害最严重的少数几个国家之一^[1]，其中暴雨引发的洪涝及泥石流、塌方等地质灾害在各类自然灾害中占有很大比重。据民政部发布的2017年全年自然灾害基本情况报告显示，洪涝和地质灾害所造成的直接经济损失达1 909.9亿元，占各类自然灾害造成的直接经济损失总和的63%。因此，开展暴雨灾害预评估工作，能够为政府及相关部门应急决策管理提供科学的依据，对国家防灾减灾具有重要意义。

暴雨灾害预评估工作涉及致灾因子、孕灾环境、承灾体等方面^[2]。降雨作为主要的致灾因子^[3]，是暴雨灾害发生的诱发因素。因此，降雨的发生强度和预报准确度，很大程度上决定了预评估结果中暴雨灾害发生的严重性和可能性。其中，暴雨预报的准确度可通过对预报结果进行检验获取。目前对数值模式降水预报的检验和评估方法有很多^[4-8]，定量降水预报评分普遍采用二分类事件检验方法，将暴雨预报与观测点进行匹配，统计发生或者不发生频数，计算预报评分，如成功指数(Threat Score, 简称TS)评分和公平成功指数评分(Equitable Threat Score, 简称ETS)评分等^[9-12]，它们从统计学角度对预报准确、空报、漏报站点数进行计算，能够较好地反映模式降水预报的准确性，ETS还对随机降水预报概率做了考虑，这些评分指数简明扼要，特别是TS评分，是中国常用的暴雨预报检验评分。另外, 德国美因兹大学大气物理学院研发的SAL方法^[13]可以从总雨带及其内部结构两个方面，对雨带的预报从强度（amplitude，简称A）、位置（location，简称L）、结构（structure，简称S）三个降水预报最关键的因素进行效果检验，方法设计科学，与预报员和科研人员的分析思路一致。公颖采用SAL方法对不同的预报模式的定量降水预报的强度、位置、结构三方面进行评估^[14]。尤凤春等采用的MODE方法对北京不同类型天气系统造成的降水进行模式预报产品的客观检验^[15]，他们为模式研发人员提供了更多有用信息。这些方法确实能从不同的角度定性和定量的反应数值预报模式降水预报的好坏。

但这些方法并不是从暴雨灾害预评估的角度来考虑的。本文借鉴TS评分和SAL方法中的思想和经验，提出了一个新的降水预报准确度的计算方法，以期为暴雨灾害预评估工作提供参考。

1 降水准确度方法和数据资料 1.1 降水准确度方法介绍

以暴雨灾害预评估工作的需求为着眼点，通过比较某一观测站实况降水强度与模式降水预报强度之间的关系，借鉴SAL中强度检验的思想，采用欧氏距离度量的方法，建立以观测站点为基础检验模式降水预报准确度(P)的公式为：

$ p = \left( {1 - \frac{{|o - f|}}{{o + f}}} \right) \times {\left( {\frac{o}{{\max \left( {{o_0}, o} \right)}}} \right)^\alpha } $

(1)

其中，o是观测站点的实况降水，f是插值到对应观测站点的模式预报降水，o₀是暴雨级别降水量阈值(如6 h的暴雨级别降水量的阈值定为25 mm), α是大于0的系数。

降水预报准确度公式(1)说明如下：

公式(1)中乘号之前$\left( {1 - \frac{{|o - f|}}{{o + f}}} \right)$的含义：通过欧氏距离来度量观测站点上o、f 的距离|o - f |与o、f 之和(o + f)的比值得到o与f之间的近似程度，当o与f越接近降水预报准确度越高，反之准确度越低。另外，假定|o - f |一定的情况下，随着o或f的值越大，$\left( {1 - \frac{{|o - f|}}{{o + f}}} \right) $的值就越大。由于降雨量越大，致灾的可能性越高，因此公式中暗含着对大量级的降水预报准确度给予更高的评分权重。

公式(1)中乘号之后$ {\left( {\frac{o}{{\max \left( {{o_0}, o} \right)}}} \right)^\alpha }$的含义：当实际观测降水较大时，导致灾害的可能性比较大，而当实际观测降水较小时，导致灾害的可能性比较低，那么从为暴雨灾害预评估工作服务的角度出发，o较小时的预报降水准确度相对于o较大时的准确度的价值就低一些，因此在公式(1)中引入暴雨灾害降水惩罚项${\left( {\frac{o}{{\max \left( {{o_0}, o} \right)}}} \right)^\alpha } $，表明当实况降水o小于暴雨降水阈值o₀时，降水准确度的评分需要被惩罚。

然而当预报降水和观测降水分别位于暴雨降雨阈值o₀两侧时，表明降水预报对暴雨灾害预评估工作具有误导性，故由公式(1)计算的其降水预报准确度需要被施以惩罚：

$ p = \beta \times p{\rm{ }}\;\;\;\;if((f - {o_0}) \times (o - {o_0}) < 0) $

(2)

其中，β是准确度惩罚性系数（0~1）。

公式(2)的含义为：当降水预报小于而观测降水大于暴雨级别降水阈值时，那么将会影响到暴雨气象服务的效果，故其降水预报准确度需要被惩罚；同理，如果降水预报大于而观测降水小于暴雨级别降水阈值时，那么将会过度增加暴雨气象服务的工作，浪费人力物力资源，故其降水预报准确度也需要被惩罚。

当观测降水与预报降水分别处于暴雨降水的阈值两侧时，对应的降水预报准确度最大值为β，所以β不能过小，本文选择β = 0.8。

1.2 系数α的敏感性分析

为了分析公式(1)和(2)中的系数α和系数β的取值对降水预报准确度p的敏感性影响，本文设计了一个理想试验：选择一组理想数据，实况降水o为从1 mm到100 mm，间隔1 mm，共100个数据，预报降水f也是100个从1 mm到100 mm一组数据，这里暴雨级别降水阈值o₀ = 25 mm。

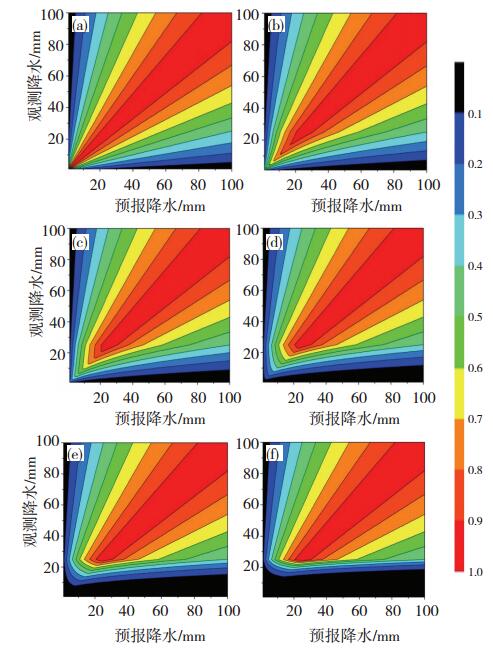
公式(1)的系数α决定着暴雨级别降水惩罚项的权重，影响暴雨灾害预评估所依赖的降水预报准确度，需要选择一个合适的参数。图 1给出了当系数α =(0.0, 0.25, 0.5, 1.0, 2.0, 4.0)时，100个预报降水相对于100个实况降水利用公式（1）计算的降水预报准确度p的分布。如图 1a所示，当α = 0.0时，表示不考虑暴雨灾害降水惩罚项权重，随着实况降水和预报降水的值从1 mm到100 mm逐渐增加时，降水准确度p大值的权重越来越大(图 1a中大值分布越来越多)，这表明公式(1)设计的目的主要是针对大量级降水给予更高评分的理念，服务于暴雨灾害预评估的应用。但当α = 0.0时，公式(1)会存在一定的缺陷：即当预报降水较大时，同样也给予p的权重越来越大，但对于观测较小时会过高估模式预报降水的准确度，从而误导暴雨灾害预评估的结果。所以需要在公式(1)中增加暴雨级别降水惩罚项${\left( {\frac{o}{{\max \left( {{o_0}, o} \right)}}} \right)^\alpha } $，如图 1b所示，当α = 0.25时，可以看出p的权重更多由实况降水来主导，尤其当α = 4.0时非常明显(图 1f)。通过对图 1中不同系数α对预报准确度p的分布情况的分析和比较，当α =(2.0, 4.0)时，观测降水低于20时，p的值基本上小于0.3，这说明暴雨级别降水惩罚项的权重过大；而当α = 0.25时，暴雨级别降水惩罚项的权重过小；当α =(0.5, 1.0)时，暴雨级别降水惩罚项的权重相对比较合适。本文选择α = 0.5作为暴雨级别降水惩罚项系数。

1.3 数据资料

本文选取欧洲中期天气预报中心(ECMWF)模式和美国国家环境中心(NCEP)全球模式2012—2014年4—9月20时起报（北京时，下同）的6 h预报降水进行预报效果对比分析，即14时6 h降水观测对应的是模式12~18 h累计降水预报，20时6 h降水观测对应的是模式18~24 h累计降水预报, 02时6 h降水观测对应的是模式24~30 h累计降水预报，08时6 h降水观测对应的是模式30~36 h累计降水预报（表 1）。检验实况为全国6 h地面降水观测资料。

2 个例分析

以2014年3月27—31日华南地区的强降水过程为例，其中广东大部、广西北部和东部等地降水100~ 180 mm，广东珠三角及附近地区和广西梧州局地降水量200~300 mm，广州海珠区新港街降水量达360 mm。广东为降水最强的省份，约75%的县市出现了50 mm以上日降水量，全省平均降水量达114.4 mm。南方多地出现城市内涝和山体滑坡等灾害，据民政部统计，截至2014年4月2日9时，广东、广西、福建、江西、湖南、重庆、贵州7省（区、市）128.5万人受灾，23人死亡，3人失踪；农作物受灾面积58.6 khm²；直接经济损失8.8亿元。其中，广东13人死亡，3人失踪。

下面以广东和广西共177个观测站点为暴雨灾害预评估的研究对象。本文以暴雨黄色预警信号：6 h内降雨量将达50 mm以上，或者已达25 mm以上且降雨可能持续，作为致灾性降雨过程。这里公式(1)和公式(2)中的系数取α = 0.5，β = 0.8和o₀ = 25 mm。

模式降水准确度的具体计算流程为：首先把模式预报降水插值到观测站点上，再利用公式1和2来计算每个站点对应的降水预报准确度，然后再进行检验和分析。

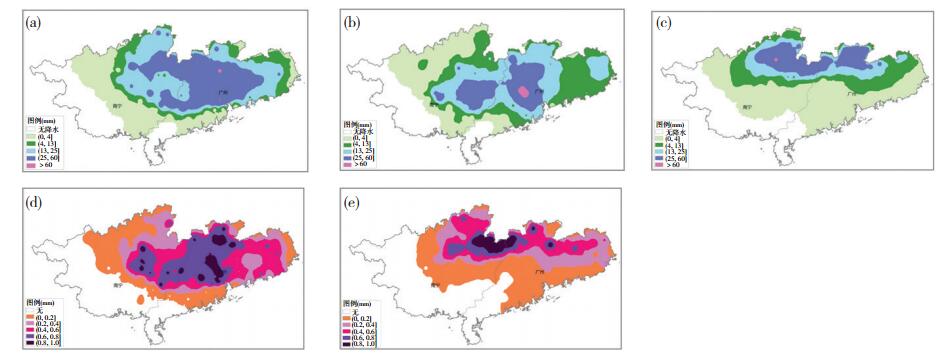
2.1 降水准确度定性分析

2014年3月31日02—08时的ECMWF降水准确度分布(图 2d)的大值区(大于0.6)主要集中在广西东部和广东西部偏北位置，该区域实况观测(图 2a)降水量级较大，且对应的ECMWF模式降水在该区域的预报效果(图 2b)与观测降水一致，所以其降水准确度评分较高，体现了公式(1)和(2)是以暴雨灾害预评估服务为目的评分。另外，NCEP降水准确度(图 2e)分布的大值区(大于0.6)主要集中在广西东北部，该区域实况观测(图 2a)降水量级较大，且对应的NCEP模式降水在该区域的预报效果(图 2c)与观测较为一致，所以其降水准确度评分较高。但NCEP模式降水预报效果总体上比ECMWF的要差，所以NCEP模式降水准确度评分总体上也不如ECMWF。另外当观测降水很小(图 2a中广西西部)的区域，虽然模式的预报也很小(图 2b广西西部)，但其相应的降水准确度的评分也很小(小于0.2)，这说明本文研究的降水准确度主要是针对暴雨灾害服务为出发点的，而对那些对灾害无影响的很小的降水，不是致灾性降雨服务的关注重点，因此会对其降水准确度评分进行惩罚。

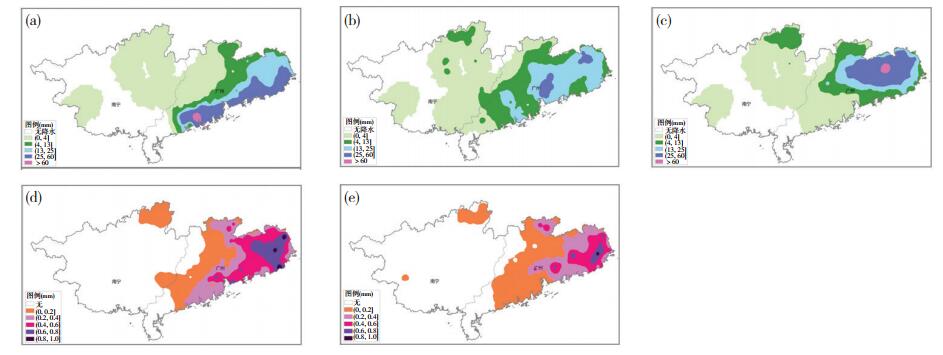
另外一个个例2014年3月31日08—14时的ECMWF降水准确度(图 3d)的分布的大值区(>0.6)主要集中在广东东部，NCEP降水准确度(图 3e)的分布的大值区(>0.6)也主要集中在广东东部，但范围比ECMWF分布的小。从降水预报上看，ECMWF降水预报(图 3b)显然与观测更一致，好于NCEP降水预报(图 3c)，所以ECMWF降水准确度评分(图 3d)总体上也好于NCEP的(图 3e)。

2.2 降水准确度定性定量检验

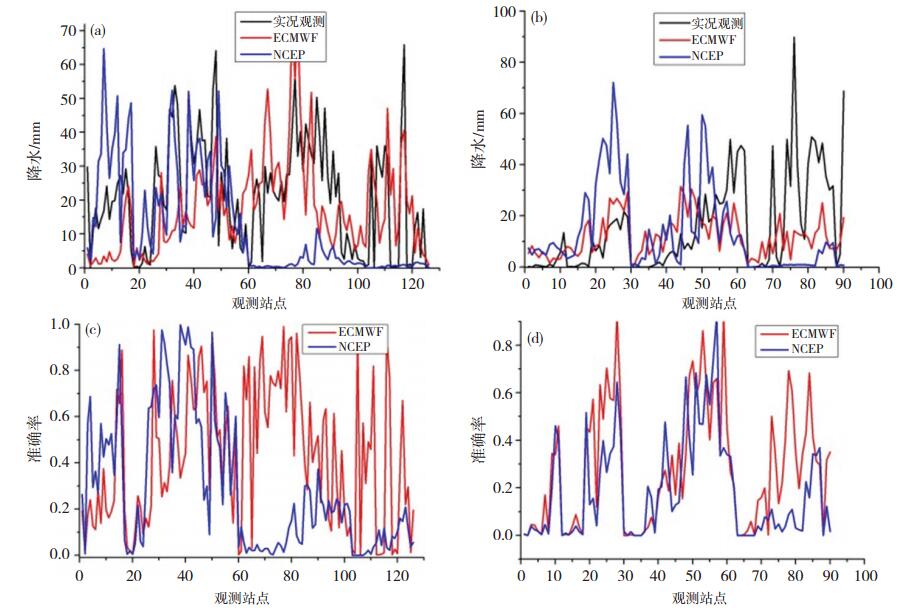
图 4给出了广东和广西对应的ECMWF模式和NCEP模式的降水准确度的定量检验结果，从2014年3月31日02—08时降水预报(图 4a)和降水准确度(图 4c)中可以看出：1)第1—16个站点的NCEP模式降水预报比实况降水多，而ECMWF模式降水预报则比实况降水少，所以根据公式(1)和(2)中针对模式降水比观测降水更小时，施以的惩罚系数更多，所以第1—16个站点NCEP的准确度评分要好于ECMWF(图 4c)；2)第17—60个观测站对应的ECMWF模式和NCEP模式的降水预报都与实况降水比较接近，因此它们的降水准确度评分都很高(图 4c)，最大评分为0.99；3）第61— 126个观测站对应的NCEP模式的降水预报都比实况降水小很多，几乎为0，因此它的降水准确度评分都极低，而ECMWF模式的降水在大部分站点的降水预报更接近于观测降水，因此其降水准确度评分显然好于NCEP (图 4c)；4)总之这126个观测对应的ECMWF模式的平均降水准确度为0.429，NCEP模式的平均降水准确度为0.289，因此ECMWF模式的降水预报效果好于NCEP模式。

另外，从2014年3月31日08—14时降水预报(图 4b)和降水准确度(图 4d)分析中也得到了相似的结论：即ECMWF模式的降水预报明显要比NCEP模式更接近于实况降水，因此ECMWF模式的降水准确度的评分(平均为0.281)也明显好于NCEP模式评分(平均为0.187)。

从这两个个例分析可以看出，降水准确度即能很好地检验模式降水预报效果的好坏，并且针对致灾性降水的检验给予了更高的权重，从而为暴雨灾害预评估服务提供更可靠的依据和参考。

3 批量结果检验

本文选取2012—2014年ECMWF模式和NCEP模式20时起报6 h降水预报进行降水准确度对比分析，实况为江南华南地区七省（湘赣浙闽粤桂黔）59个气象观测站对应时次地面6 h降水观测资料，与模式降水对应关系如表 1所示。试验选择的区域分别为湖南(98个站)、江西(87个站)、浙江（72个站）、福建(71个站)、广东(86个站)、广西(92个站)、贵州（84个站）7省（自治区）。有效个例挑选办法为：选取该检验区域中6 h降水量大于等于13 mm（大雨量级）的站点不少于5个站的时次，并且大雨量级的站点总数超过试验区域总站数的15%。

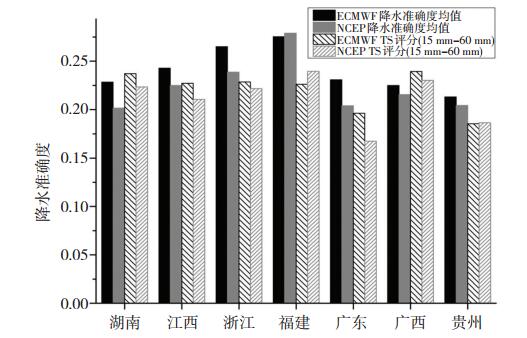
批量试验的降水准确度的统计和计算流程为：首先，单个时次的预报降水准确度计算流程与第2节中流程一致，公式(1)和公式(2)中的系数取α = 0.5，β = 0.8和o₀ = 25 mm；然后分别计算这7个省（湘赣浙闽粤桂黔）每个有效个例的平均降水准确度（即所有站点降水准确度的平均值）；最后对7个省分别计算TS评分，为了和降水准确度进行对比，这里TS评分将大雨(13~25 mm)与暴雨(25~60 mm)合并起来统计的，这样其评分结果比单独统计大雨和暴雨的都要高。图 5分别给出了这7个省ECMWF模式和NCEP模式的降水准确度的均值和TS评分统计结果，从中可见，湘赣浙粤桂5个省的ECMWF模式的降水准确度都要好于NCEP，并且其TS评分也好于NCEP，福建省则相反，而贵州省的ECMWF模式的降水准确度略好于NCEP，但其TS评分略差于NCEP，由此说明降水准确度针对模式降水的统计评判结果与TS评分基本上一致的，对模式预报降水的评估是合理的。

降水准确度是针对每个时次每个站点进行单独计算的，可以给出一个更详细的站点水平分布图(图 2d和2e)，因此相对于TS评分其更适用于针对暴雨灾害的相关预评估服务。

4 结论和建议

本文从暴雨灾害预评估的需求出发，设计了一个针对致灾性暴雨的降水预报准确度计算方法，对不同预报模式的降水准确度进行计算，为暴雨灾害预评估提供参考。主要结论如下：

(1) 通过理想试验确定了降水准确度公式的敏感性参数，并分析和解释了该方法的原理和意义，并通过个例试验验证了该方法的合理性；

(2) 利用该评估方法对ECMWF模式和NCEP模式的批量试验结果进行降水准确度的统计检验，与TS评分结果一致，说明本文设计的降水准确度评分针对模式降水的检验是合理的，且适合于针对暴雨灾害的预评估服务。

本文在选择暴雨降水阈值o₀时，暂时选用6 h暴雨级别的降水量，后期希望通过灾情数据和致灾雨量结合，来定义o₀的取值。另外，本文下一步拟结合该方法得到的降水准确度为暴雨灾害预评估服务，通过其评分来调整灾害风险等级划分，并建立对应关系。