2. 中国科学院水利部成都山地灾害与环境研究所, 成都 610041;
3. 成都信息工程大学软件工程学院, 成都 610225;
4. 河海大学水文水资源学院, 南京 210098;
5. 河海大学水文水资源与水利工程科学国家重点实验室, 南京 210098
2. Institute of Mountain Hazards and Environment, Chinese Academy of Sciences, Chengdu 610041;
3. College of Software engineering, Chengdu University of Information Technology, Chengdu 610225;
4. College of hydrology and Water Recourses, Hohai University, Nanjing 210098;
5. State Key Laboratory of Hydrology-Water Resources and Hydraulic Engineering, Hohai University, Nanjing 210098
在我国,达到一定规模的泥石流沟数目超过5万条,其分布在48%的国土面积上[1-2]。泥石流作为我国最常见的山地灾害之一,平均每年导致数百人死亡,造成超过10亿元的直接经济损失,给社会经济可持续发展带来严重的威胁[3-4]。其中95%以上的泥石流均是因降水诱发,并具有一定的规律性[5]。仅2014年全国共发生泥石流灾害543起,造成显著的人员伤亡与社会经济损失[6]。2014年7月21日06时,云南省芒市芒海镇户那村民小组发生大型泥石流灾害,共造成14人死亡、6人失踪、7人受伤;灾害主要诱因为持续降水导致沟内形成大流量洪水,沟内松散土体呈过饱和状态;短时强降水(7月20日20-21时,小时降水量达到102.4 mm),为泥石流发生提供了充足水动力条件[6]。
泥石流预报作为一项重要的防灾减灾非工程措施,通过预先分析判断泥石流发生时间、位置以及规模等发布预警信息,减轻人民财产损失,受到了国内外学者广泛关注[3, 7-9]。泥石流形成条件与机理是泥石流预报的理论基础。近20 a来,在泥石流形成与启动机理尚未完全明确[3]的情况下,许多学者[5, 7, 10-15]采用统计分析的手段研究降水和泥石流事件之间的经验关系,依据常用降水参数(例如:前期降水、降水持时、强度和累计降水量等)之间的组合,确立触发该区泥石流形成的临界阈值。起初,采用单一的降水参数(临界累计降水量、降水强度等)作为泥石流的判识因子;后来,随着泥石流预报研究工作的深入,提出了降水参数之间的组合判别公式,而在美国洛杉矶Bay地区的研究工作恰恰证明了组合判别公式的必要性,利用降水的组合方式能涉及到一场降水过程中雨水在土体中的入渗和排出速率之间的平衡[1]。最为常用的Rainfall Intensity-Duration (简称ID)曲线于1980年提出后,相似的组合判别公式也应用于美国洛杉矶地区的泥石流预报[13]。另外,Bacchini和Zannoni [13]针对意大利东北部的多洛米蒂山,依据平均降水强度、持续时间和年平均降水量建立了泥石流的临界组合判别式;Pan等[14]针对缺资料区域提出基于降水量阈值的泥石流预报方法。
我国的地质灾害气象风险预警业务(2003年起,国土资源部与中国气象局联合发布)的业务模型也是基于统计学的方法,且没有区分泥石流、滑坡和崩塌灾种预报[5, 7-8, 15]。这些预报方法没有充分考虑到降水入渗与产汇流等流域水文过程对泥石流启动机制响应,仅单纯依据临界降水量,预报准确率较低。为了降低这种风险,韦方强等[16]利用模糊数学方法建立了泥石流预报的可拓模型,根据泥石流发生条件的不同,将临界降水量划分成为不同的等级范围,根据预报区域预报降水量等级范围和下垫面条件确定泥石流发生的概率。该预报方法虽然考虑下垫面对泥石流形成的影响,但并没有利用泥石流形成机理建立下垫面因子与降水因子之间的本质联系,仍未突破统计预报模式,且预报单元为网格单元,预报结果需要根据流域分析进行人工订正。
近年来,学者们开展了土体力学性质变化条件下的坡面土体稳定性分析研究,并建立了泥石流启动模型[17-20]。Iverson [17]通过试验表明,土体剪切面处的孔隙水压力波动,会造成颗粒间的接触应力失效;基于这一发现,Iverson [18]利用摩尔-库伦准则推导了泥石流启动模型,并利用United States Geological Survey (USGS)的百米水槽试验,对孔隙水压力在泥石流形成过程中所发挥的作用进行了更为深入的探讨;Cui [20]通过室内的100余次人工降水试验,建立了以土体含水量、底床坡度和细粒含量为自变量的应力状态函数来预测泥石流的发生;张万顺等[21]基于摩尔-库伦准则,提出了针对单个坡面上的泥石流形成的判定模型;上述模型研究的对象仅是单一坡面,无法判断流域尺度上是否会形成泥石流。也有意大利学者建立一个简单的水文模型,用以预测不同降水条件下的水文响应,但由于水文模型过于简单,尚未真正用于泥石流预报[3]。
用于降水诱发型泥石流预报的统计模型中,难以考虑降水入渗与产汇流等流域水文过程对泥石流启动的影响。而耦合分布式水文模型的泥石流物理预报模型能够利用地形、地质环境与水文信息,基于流域尺度上的水土耦合框架,分析在降水作用下坡面土体失稳过程以及失稳土体与流域径流混合形成泥石流过程,从而实现降水诱发型泥石流物理预报。对于泥石流预报而言,选取恰当的预报单元是预报过程中最为关键的首要步骤。目前的预报单元主要由区域向网格化方向发展。以区域为预报单元的主要代表就是ID曲线,只要预报或监测降水超过预警线,就在整个研究区内发预警,但是区域内究竟哪个位置有泥石流无法明确;预报的网格单元以韦方强等[16]提出的成因预报模型预报单元网格最为典型:将研究区离散成为3 km×3 km网格,这种方法了考虑下垫面对泥石流的影响,比仅考虑降水因素的ID法更具科学性,更重要的是预报结果可明确区域内某个位置的网格是否有泥石流灾害的发生。
泥石流主要发育在小的流域范围内,属于流域内剧烈的水土耦合过程。所以,泥石流预报单元以小流域作为预报对象更符合实际。目前成因预报方法中的网格单元无法代表流域的地貌形态和自然边界,预报结果虽然能够定位到区域内的某个位置,但是该位置内的哪个小流域是否有泥石流发生无法确定,预报员需要依据流域分析对预报结果进行二次修订,才能确定具有泥石流灾害的流域,费时费力,无法达到业务预报的时效性需求[22]。为此,本文在研究提取具备发生泥石流的潜势流域基础上,在泥石流预报模型中耦合Geomorphology-Based Hydrological Model(GBHM)分布式水文模型[23],更好考虑降水的植被冠层截留、蒸散发、下渗、产流与汇流等水文过程对泥石流启动机制的影响,选取云南省作为区域泥石流预报试验区域,建立水土耦合的泥石流预报模型,并选择2016年6月24日强降水诱发泥石流个例进行验证,以期提高泥石流的预报精度。
1 耦合分布式水文模型的泥石流预报模型降水诱发型泥石流,降水是其灾害触发因子,水文过程很大程度影响边坡稳定度和泥石流中的径流量[9]。本文的泥石流预报模型主要依据降水诱发型泥石流的基本原理,基于两个水土耦合过程构建,一是降水与坡面土体耦合,造成部分坡面土体失稳;二是流域径流与失稳土体耦合形成泥石流。泥石流预报单元基于能量条件进行潜势泥石流流域提取,水文过程由GBHM分布式水文模型模拟。
1.1 基于能量条件的潜势泥石流流域提取水土耦合的泥石流预报模型主要是预报泥石流流域发生泥石流的概率,因此需要将统计模型中的网格预报单元转变为泥石流流域单元[22]。韦方强等[16]提出,泥石流流域面积一般在不足1 km2到100 km2不等,且80%以上的泥石流流域面积小于10 km2。实地调查是评估泥石流流域发生概率是最好的方法,但对于区域尺度上的泥石流流域确定是困难的[9]。能量、松散固体物质和水是泥石流发生的三个先决条件,其中松散固体物质和水受多种因素影响,变化较快,而能量条件仅受地形影响,在较长时间内可以认为是不变的,且能量条件又是泥石流形成的决定条件。因此,能量条件可以作为判断一个流域是否具备发生泥石流的基本条件[9]。地貌条件主要为泥石流的形成提供能量。在相对高度、沟床比降、坡度、坡向、流域面积等地貌因子中,流域的相对高度既与流域的沟床比降和流域面积有密切的联系,又能独立反应流域的地貌特征。流域的相对高度大,径流容易汇集,利于泥石流的形成;在相同高差的条件下,流域面积越小,单位面积的相对高差越大,越利于泥石流的形成。因此,流域相对高度和流域面积可作为泥石流流域的判识指标, 建立基于能量条件的泥石流流域判定模型[24]。
但是在实际研究中发现,根据泥石流流域相对高度和流域面积统计分析得到的拟合关系易造成一定数量的样本遗漏。本文采用张少杰等[9]提出的建立一条既能反应相对高程与流域面积关系,又尽可能少遗漏样本的下包络线:
| $ {\rm{ln}}(dh) = 0.2553{\rm{ ln}}(A) + 2.008, A \in [0.1\;{\rm{k}}{{\rm{m}}^2}, 300\;{\rm{k}}{{\rm{m}}^2}] $ | (1) |
式(1)中,dh为流域的相对高度,A为流域面积。在下包络线上方的点,均可以判定为潜势泥石流流域。
1.2 降水作用下流域内坡面土体失稳降水入渗是影响坡面土体稳定性,最终导致浅层滑坡的关键触发因素,浅层滑坡的深度一般深0.5~ 2.0 m左右。流域内的坡面土体在雨水入渗之前,多处于非饱和状态,降水入渗使得土体含水量增加,进而造成土体的基质吸力降低,是导致坡面土体失稳的主要诱因。本文基于无限边坡模型,利用安全系数(Fs)评价坡面土体在降水入渗作用下的稳定性,浅层失稳面平行于坡面,由摩尔-库伦破坏准则控制。
由Fredlund和Rahardjo [25]提出的非饱和土抗剪强度公式如下:
| $ {\tau _f} = c + ({\sigma _n}-{u_a}){\rm{tan}}\varphi + ({u_a}-{u_w}){\rm{tan}}{\varphi ^b} $ | (2) |
式(2)中,τf为土体抗剪强度,σn为剪切面上正常应力,uw为空隙水压力,φ是土体的内摩擦角,b为无量纲指数,φb与基质吸力有关,当基质吸力较低时,该值与内摩擦角φ接近,ua是为大气压,ua = 0,c为土体的粘结力。
基于式(2),极限平衡公式可以表述如下:
| $ {F_s} = \frac{{c + ({\sigma _n}-{u_a}){\rm{tan}}\varphi + \psi {\rm{tan}}{\varphi ^b}}}{F} $ | (3) |
式(3)中,剪切面上剪切力F为重力沿平行与坡体向下的分力:
| $ F = W{\rm{sin}}\beta = {\gamma _t}{H_s}{\rm{cos}}\beta {\rm{sin}}\beta $ | (4) |
其法向应力为重力垂直于坡体的分力:
| $ {\sigma _n} = W{\rm{cos}}\beta = {\gamma _t}{H_s}{\rm{co}}{{\rm{s}}^2}\beta $ | (5) |
式(4)、(5)中,W为重力,β为坡度角,γt是土壤颗粒密度,Hs为土层厚度。
综合公式(3)-(5),可得:
| $ {F_s} = \frac{{{\rm{tan}}\varphi }}{{{\rm{tan}}\beta }} + \frac{{c + \psi {\rm{tan}}(\eta \varphi )}}{{{\gamma _t}{H_s}{\rm{cos}}\beta {\rm{sin}}\beta }} $ | (6) |
式(6)中,本文取η = 1,ψ = ua - uw为基质吸力,是土体含水量的函数,由方程由Van Genuchten模型描述[26]:
| $ {S_e} = {\left[{\frac{1}{{1 + {{(\alpha \times \psi )}^n}}}} \right]^m} $ | (7) |
| $ {S_e} = \frac{{\theta-{\theta _r}}}{{{\theta _s}-{\theta _r}}} $ | (8) |
式(7)、(8)中,Se为饱和度,θs和θr分别表示土体的饱和含水量和残余含水量,θ为当前时刻的土体含水量,α、n和m为曲线形状参数,且n=1-1/m。
1.3 流域径流与失稳土体耦合降水形成的径流与失稳土体间的进一步耦合,会形成流域泥石流。该过程十分复杂,目前难以通过数值模型或物理模型具体描述,从野外观测来看,泥石流是具有一定密度的水土混合物。因此,选取水土混合物密度来区分含沙水流、稀性泥石流和粘性泥石流的重要指标,代表着泥石流固体物质数量[9]。因此,利用径流和失稳土体耦合后的水土混合物密度ρ进行流域泥石流预报:将自然界中形成泥石流的水土混合物密度(一般在1.1~2.3 g.cm-3)[27]划分成一系列的参考区间,根据ρ所落的标准泥石流的水土混合物密度参考区间,确定泥石流发生概率大小。丰富的松散固体物质是流域泥石流发生的基本条件,水土混合物密度ρ越大,表明预报降水造成的松散固体物质总量越丰富,泥石流发生概率越高,因此可以通过水土混合物密度值变化预报泥石流发生的危险度[12]。
| $ \rho = \frac{{{\rho _w}{v_w} + {\rho _s}{v_s}}}{{{v_w} + {v_s}}} $ | (9) |
式(9)中,ρ, ρw和ρs分别是水土混合物、水体和土体颗粒密度(ρs =2.7 g.cm-3),vw和vs分别是降水条件下的水体总量和失稳土体总量,ρ与流域泥石流形成概率之间的关系见表 1。
|
|
表 1 泥石流形成的概率与其对应的混合物密度[27] Table 1 Occurrence probability of debris flow and its corresponding mixture density (from 27th reference in the paper) |
由水土耦合方程(9)可知,为了利用水土混合物ρ实时发布流域泥石流预报,需要实时评估流域内降水造成的失稳土体总量vs和径流总量vw。为此,本文以非饱和土极限平衡方程(3)和GBHM分布式水文模型为手段,获取上述的两个关键值。
1.4.1 GBHM分布式水文模型杨大文教授在1998年根据流域地形地貌特性研发了基于地貌的水文模型(Geomorphology based hydro⁃ logical model, 简称GBHM) [23]。分布式水文模型基于地貌将流域产汇流过程归纳成“山坡-河网”系统,并采用数理方程来描述包括产汇流机制的流域水文过程[28-29]。模型是一个建立在DEM与GIS基础上的分布式物理水文模型,主要由流域空间信息集、流域水文计算模块、模型输入模块和模型输出模块四部分组成。
1.4.2 基础数据区域土壤含水量推求在进行水文过程模拟时,需要首先设定区域内的土壤含水量初始值。然而,受到降水入渗、蒸散发作用的影响,任意时刻的土壤含水量初值是无法直接判定的。在中国,冬季一般是少雨季节,土壤表层较为干燥,接近土体的残余含水量。鉴于此,本文的计算时间从预报当年的1月1日起,区域内的表层土壤含水量设置为与土地类型相对应的残余含水量值。利用中国气象局实况降水数据,从1月1日起至泥石流预报的时刻止,通过水文模型计算为泥石流预报提供较为准确的土壤含水量初值。
1.4.3 土体失稳总量vs推求流域内离散网格单元的非饱和土层厚度为2 m,划分成为7层,每层厚度分别为0.05 m、0.1 m、0.15 m、0.2 m、0.3 m、0.5 m、0.7 m,利用极限平衡方程(3)计算每层土的安全系数,通过计算流域内每个网格的失稳深度,实时评估土体失稳总量vs。
由非饱和土的极限平衡公式可知,Fs主要是由基质吸力和土体粘结力控制,而土体含水量的增加会导致基质吸力和土体粘结力的降低,当Fs < 1时,网格单元失稳。所以,土体失稳总量的实时评估,主要在于流域内的土体含水量和基质吸力(即负孔隙水压力)的实时计算。在此,以分布式水文模型GMHM获取的土体含水量和基质吸力为动态输入量,确定流域范围内的每个网格的每层土的安全系数Fs,进而实时评估流域的土体失稳总量。
| $ Su{m_{{\rm{ins}}}} = \sum\limits_{t = 1}^{24} {\sum\limits_{i = 1}^{{N_{{\rm{ins}}}}} {{A_i} \times {D_{{\rm{ins}}}}} } $ | (10) |
式(10)中,Sumins为t时刻的土体失稳总量,Dins为网格的失稳深度,Ai为网格的面积,Nins为t时刻的失稳网格总量。
1.4.4 径流总量的实时评估GBHM分布式水文模型基于超渗产流机制,利用曼宁公式描述坡面流,实时计算降水作用下的每个网格产生的径流深度Dr,进而求得径流总量vw。
| $ Su{m_r} = \sum\limits_{t = 1}^{24} {\sum\limits_{i = 1}^n {{A_i} \times {D_r}} } $ | (11) |
式(11)中,Sumr为t时刻的径流总量,Dr为网格的径流深度,Ai为网格的面积,N为流域内的总的网格数。
1.4.5 水土混合物密度实时评估与泥石流发生概率预报结合方程(9~11)便可计算出每条潜势泥石流流域在t时刻的水土混合物密度ρ,根据ρ值,结合泥石流形成概率与对应混合物密度表(表 1),判断区域内每条潜势泥石流流域发生泥石流的概率大小,依据不同的泥石流预警等级,对每条潜势泥石流流域标记与预警等级相对应的预警颜色,发布泥石流预警等级信息。
2 研究区域与灾情在我国,泥石流是强降水诱发的最为常见的地质灾害之一。图 1给出1949-2002年全国泥石流灾害空间分布图(灾情数据来自国土资源部地质环境监测部门)。从中可见,除上海外,我国各省均有泥石流灾害发生。泥石流在空间分布上具有规律性,最显著的特征是沿着我国青藏高原的东部带状分布,青海东北、甘肃南部、四川盆地西部和云南北部均是我国泥石流灾害发生频繁的地区。因此,本文选择云南省为研究区域,进行耦合分布式水文模型的泥石流预报建模。

|
图 1 1949-2002年全国泥石流灾害发生地点空间分布 Fig. 1 Spatial distribution of occurrence places of national debris flow hazards from 1949 to 2002. |
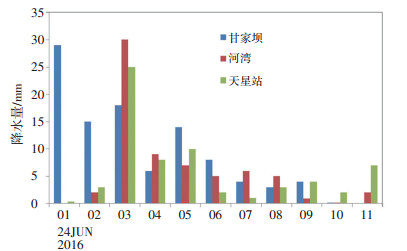
根据中国气象局与中国地质环境监测院资料显示,北京时间2016年6月24日00-24时(北京时,下同),云南省东北部境内普降暴雨,最大累计降水量发生在云南省与四川省交界的大雪山雪山村自动站(站号为835580),共125 mm,其最大降水强度为44 mm·h-1,出现03-04时。此次暴雨过程诱发了云南省昭通市境内发生3起小型泥石流灾害(表 2),共造成约65万元的财产损失。南厂村、黄沙坪子和祥云三个灾害点在泥石流灾害发生前最大降水强度分别为29 mm·h-1、30 mm·h-1和25 mm·h-1,图 2给出灾害发生前最临近雨量站逐小时降水量。本文以该次泥石流灾害事件为例,应用耦合分布式水文模型的泥石流物理预报模型进行预报实验,并评估其预报的准确率。
|
|
表 2 2016年6月24日云南昭通境内泥石流灾情信息表 Table 2 The information on debris flow hazards in the Zhaotong city of Yunnan Province on 24 June 2016 |
|
图 2 泥石流灾害发生前灾害点最临近雨量站逐小时降水量 Fig. 2 Hourly precipitation at the nearest rainfall stations before debris flow hazards occur. |
利用ArcGIS中的水文分析工具提取研究区内的小流域,利用判识公式(1)对划分好的小流域进行泥石流流域判识。
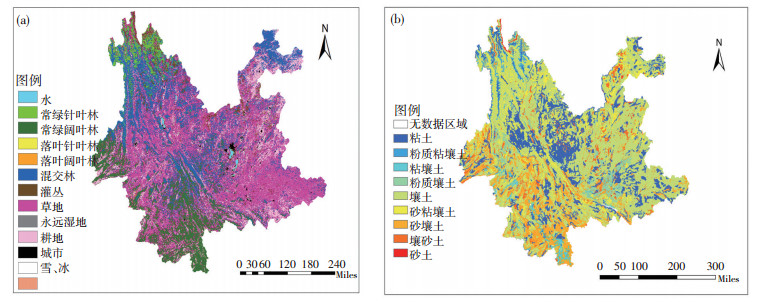
3.2 数据准备 3.2.1 GBHM计算所需数据GBHM分布式水文模型计算过程中所需的基础数据主要包括:数字高程模型(DEM)、流域降水空间分布数据、土地利用类型、土壤类型等[23]。其中,研究区域的DEM数据基于USGS提供的30" × 30"分辨率的原始数据;流域降水空间分布数据根据中国气象局地面降水自动站数据,应用反距离权重法插值到30" × 30"分辨率的格点上;土地利用类型、土壤类型和土层厚度30" × 30"分辨率数据从Food and Agriculture Organization of the United Nations (FAO,http://www.fao.org/geonetwork/srv/en/main.home)数据库直接获取。图 3、4分别给出利用ArcGIS建立云南省30" × 30"分辨率的DEM和土地利用类型、土壤类型图。云南省自然环境复杂,地形主要以山地为主,明显分为三个梯层:西北部为第一梯层,中部高原为第二梯层,南部、东南和西南部为第三梯层,平均递降率达到6 m·km-1。全省土地利用类型主要为林地,占全省总面积比达到57.8%, 土壤组成中壤土占56.6%,主要分布在云南东部和西北部。

|
图 3 云南省的DEM (单位: m) Fig. 3 DEM data (unit: m) in Yunnan Province. |
|
图 4 云南省土地利用类型(a)和土壤类型(b)分布图 Fig. 4 The distribution of (a) landuse and (b) soil type in Yunnan Province. |
本文中,由于难于获取长序列小流域水文资料进行水文模型的率定与检验,GBHM水文模型参数取值主要通过流域遥感数据直接先验获取(表 3)。
|
|
表 3 GBHM水文模型主要参数先验估算方法 Table 3 The a priori parameter estimation methods of GBHM hydrological model |
根据云南省地质图,获取云南省的岩性分布,并依据岩石力学手册对不同岩性的力学参数(土体粘结力c、内摩擦角φ)进行赋值,利用重采样技术获取相应的网格数据。本文采用Van Genuchten模型[9, 26]建立非饱和土基质吸力与土体含水量之间的关系,模型计算所用的土水特征曲线形状参数a和n根据云南省内的土壤类型分布,由IGBP-DIS(International Geosphere-Bio⁃ sphere Programme, Data and Information System)的全球土壤数据产品(http://www.dAac.ornl.gov)获取。
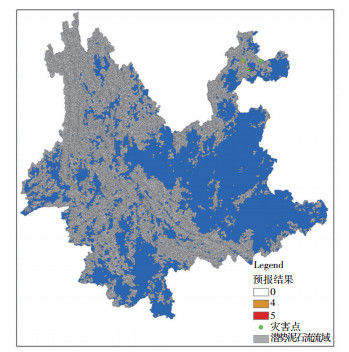
3.3 结果验证使用的实况降水数据来自于中国气象局地面自动站,并采用反距离权重法插值到与模型输入相一致的空间分辨率上。模型预报了2016年6月24日云南省内各个小流域发生泥石流的概率,并根据表 1生成相应的预警等级颜色。从6月24日00-24时的24 h预报结果中,分别选取了具有代表性的3个时间段泥石流预报结果,分别是6月24日的08- 09时,09-10时,11-12时。图 5给出云南省在这三个时段的泥石流预报结果合成图,从中可见,耦合分布式水文模型的泥石流预报模型成功预报出6月24日沙坪子和祥云两处的泥石流,发出5级红色预警和4级橙色预警信息,并一直持续至泥石流发生。泥石流模型在01时水土混合物密度就达到2.03 g.cm-3,为5级红色预警,与实际的泥石流观测资料相近。而漏报的南厂村临近自动站24日00-08时累积降水量为97 mm,最大雨强为29 mm·h-3,发生在距离泥石流发生7 h前。主要原因是,一方面临近触发降水量与其他相比量级较小;另一方面该区域地形比较复杂,利用相对简单的反距离权重法插值得到的空间降水难以准确考虑降水的空间分布,且耦合分布式水文模型的泥石流预报模型也还需要在机理上进一步改进。
|
图 5 云南省2017年6月24日08-09时、09-10时、11-12时泥石流预报结果合成图 Fig. 5 Forecasting results of debris flow in Yunnan Province from 08:00 BT to 09:00 BT, from 09:00 BT to 10:00 BT and from 11:00 BT to 12:00 BT on 24 June 2016. |
耦合分布式水文模型的泥石流物理预报模型运用泥石流形成机理建立了降水和下垫面之间的本质联系。本文利用基于能量条件的泥石流流域判定模型对云南省进行了潜势泥石流流域的提取,利用耦合分布式水文模型的泥石流预报模型预报区域内的每条潜势泥石流流域发生泥石流的概率大小,形成了基于流域水土耦合机制的区域泥石流预报方法。以云南省2016年6月24日的典强降水过程为研究实例,预报了云南省区域内每条潜势泥石流流域发生泥石流的概率,利用国土资源部地质环境监测院提供的泥石流灾情信息验证了模型在区域尺度上应用的精度和适用性。
(1) 耦合分布式水文模型的泥石流预报模型在云南省区域尺度上的6月24日的泥石流预报中取得良好的预报精度,成功预报出两个泥石流灾害。该模型可以精确到区域内某条泥石流沟,在区域尺度泥石流预报上具有较好的适用性。模型虽然在本文区域个例中预报应用效果良好,还需要在更多的预报个例中进一步验证。
(2) 水土耦合的泥石流预报模型的主要输入强迫为大气降水。本文使用的降水数据来自中国气象局地面自动站插值而成的格点降水资料。目前,雷达、卫星与地面自动站多源降水融合的定量降水估测(QPE)在反映空间降水分布和降水量估计上具有明显优势,技术已经相对成熟,并已经在我国气象部门业务化,时间分辨率已经达到30 s,空间分辨率为0.05°× 0.05°。这为提高模型输入降水的空间分布和量级的精度提供了有利的途径。
本文中用于模拟水文过程的水文模型为GBHM分布式水文模型。由于缺乏流域历史实况资料,模型参数直接来自于先验估计值,直接应用会出现一定的偏差[31]。另外,GBHM分布式水文模型反映的是超渗产流机制,而在实际的山洪泥石流过程中,是伴随着蓄满与超渗两种产流机制的[31-35]。如何在耦合分布式水文模型的泥石流模型中结合两种产流机制优势并利用长序列历史数据率定模型参数,进一步能够考虑我国复杂下垫面条件导致的径流形成物理机理的产汇流模型,是泥石流机理预报下一步着重改进的方向之一[28-29, 31, 33-34]。
| [1] |
唐邦兴. 中国泥石流[M]. 北京: 商务印书馆, 2000.
|
| [2] |
陈晓清, 崔鹏, 韦方强. 泥石流起动原型试验及预报方法探索[J]. 中国地质灾害与防治学报, 2006, 17(4): 73-78. DOI:10.3969/j.issn.1003-8035.2006.04.017 |
| [3] |
崔鹏, 高克昌, 韦方强. 泥石流预测预报研究进展[J]. 中国科学院院刊, 2005, 20(5): 363-369. DOI:10.3969/j.issn.1000-3045.2005.05.006 |
| [4] |
李媛, 曲雪妍, 杨旭东, 等. 中国地质灾害时空分布规律及防范重点[J]. 中国地质灾害与防治学报, 2013, 24(4): 71-78. |
| [5] |
薛建军, 徐晶, 张芳华, 等. 区域性地质灾害气象预报方法研究[J]. 气象, 2005, 31(10): 24-27. DOI:10.7519/j.issn.1000-0526.2005.10.006 |
| [6] |
国土资源部地质灾害应急技术指导中心. 2014年度全国重大地质灾害事件与应急避险典型案例[M]. 北京: 地质出版社, 2015.
|
| [7] |
刘传正, 刘艳辉. 地质灾害区域预警原理与显式预警系统设计研究[J]. 水文地质工程地质, 2007(6): 109-115, 125. DOI:10.3969/j.issn.1000-3665.2007.06.026 |
| [8] |
刘传正, 刘艳辉, 温铭生, 等. 中国地质灾害区域预警方法与应用[M]. 北京: 地质出版社, 2009.
|
| [9] |
Zhang Shaojie, Wei Fangqiang, et al. A Regional-Scale Method of Forecasting Debris Flow Events Based on Water-Soil Coupling Mechanism[J]. J Mt Sci, 2014, 11(6): 1531-1542. DOI:10.1007/s11629-013-2906-z |
| [10] |
Caine N. The Rainfall Intensity-duration Control of Shallow Landslides and Debris Flows[J]. Geografiska Annaler, Series A, Physical Geograpy, 1980, 62(1-2): 23-27. DOI:10.1080/04353676.1980.11879996 |
| [11] |
Campbell R H. Debris flows originating from soil slips during rainstorms in Southern California[J]. Quarterly Journal of Engineering Geology & Hydrogeology, 1974, 7(4): 339-349. |
| [12] |
Cannon S H, Ellen S D. Rainfall Conditions for Abundant Debris Avalanches, San Francisco Bay region[J]. California Geo, 1985, 38(12): 267-272. |
| [13] |
Bacchini M, Zannoni A. Relations between Rainfall and Triggering Debris-Flow:Case Study of Cancia (Dolomites, Northeastern Italy)[J]. Natural Hazards and Earth System Sciences, 2003, 3: 71-79. DOI:10.5194/nhess-3-71-2003 |
| [14] |
Pan H L, Huang J C, Wang R, et al. Rainfall Threshold Calculation Method for Debris Flow Pre-Warning in Data-Poor Areas[J]. Journal of Earth Science, 2013, 24(5): 854-862. DOI:10.1007/s12583-013-0377-3 |
| [15] |
刘艳辉, 刘传正, 温铭生, 等. 中国地质灾害气象预警模型研究[J]. 工程地质学报, 2015, 23(4): 738-746. |
| [16] |
韦方强, 汤家法, 谢洪, 钟敦伦. 沟谷相结合的泥石流预报及其应用[J]. 山地学报, 2004, 22(3): 321-325. DOI:10.3969/j.issn.1008-2786.2004.03.011 |
| [17] |
Iverson R M, LaHusen R G. Dynamic Pore-Pressure Fluctuations in Rapidly Shearing Granular Materials[J]. Science, 1989, 246(4931): 796-799. DOI:10.1126/science.246.4931.796 |
| [18] |
Iverson R M, Reid M E, LaHusen R G. Debris-Flow Mobilization from Landslides[J]. Annu Rev Earth Planet, 1997, 25: 85-138. DOI:10.1146/annurev.earth.25.1.85 |
| [19] |
Berti M, Simoni A. Experimental Evidences and Numerical Modeling of Debris Flow Initiated by Channel Runoff[J]. Landslides, 2005, 2: 171-182. DOI:10.1007/s10346-005-0062-4 |
| [20] |
Cui P. Study on condition and mechanisms of debris flow initiation by means of experiment[J]. Chinese Science BuUetin, 1992, 37(9): 759-763. |
| [21] |
张万顺, 乔飞, 崔鹏, 等. 坡面泥石流起动模型研究[J]. 水土保持研究, 2006, 13(4): 146-149. DOI:10.3969/j.issn.1005-3409.2006.04.047 |
| [22] |
张少杰, 江玉红, 杨红娟, 等. 基于水文过程的泥石流预报中前期有效降水量的确定方法[J]. 水科学进展, 2015, 26(1): 34-43. |
| [23] |
Yang D W, Herath S, Musiake K. A Hillslope-Based Hydrological Model Using Catchment Area and Width Function[J]. Hyrological Sciences Journal, 2002, 47(1): 231-243. |
| [24] |
熊俊楠. 基于遥感与GIS的精细化区域泥石流风险评估[D]. 北京: 中国科学院大学, 2013
|
| [25] |
Fredlund D G, Rahardjo H. Soil Mechanics for Unsaturated Soils[M]. New York: John Wiley & Sons Inc, 1993: 217-231.
|
| [26] |
魏义长, 刘作新, 康玲玲, 等. 土壤持水曲线van Genuchten模型求参的Matlab实现[J]. 土壤学报, 2004, 41(3): 380-386. DOI:10.3321/j.issn:0564-3929.2004.03.009 |
| [27] |
康志成, 李焯芬, 马蔼乃, 等. 中国泥石流研究[M]. 北京: 科学出版社, 2004.
|
| [28] |
包红军, 王莉莉, 李致家, 等. 基于混合产流与二维运动波汇流分布式水文模型[J]. 水电能源科学, 2016, 34(11): 1-4, 21. |
| [29] |
Bao H J, Wang L L, Zhang K, Li Z J. Application of a developed distributed hydrological model based on the mixed runoff generation model and 2D kinematic wave flow routing model for better flood forecasting[J]. Atmospheric Science Letters, 2017, 18(7): 284-293. DOI:10.1002/asl.2017.18.issue-7 |
| [30] |
Land Data Assimilation Schemes (LDAS). Mapped Vegetation Parameters[EB/OL]. [2015-07-12]. http://ldas.gsfc.nasa.gov/LDAS8th/MAPPED.VEG/LDASmapveg.shtml
|
| [31] |
包红军, 李致家, 黄小祥, 等. 基于分布式水文模型的无资料小流域山洪预报[J]. 暴雨灾害, 2017, 36(2): 156-163. DOI:10.3969/j.issn.1004-9045.2017.02.008 |
| [32] |
包红军. 基于EPS的水文与水力学相结合的洪水预报研究[D]. 南京: 河海大学, 2009
|
| [33] |
包红军, 王莉莉, 沈学顺, 等. 气象水文耦合的洪水预报研究进展[J]. 气象, 2016, 42(9): 1045-1057. |
| [34] |
包红军, 王莉莉, 李致家, 等. 基于Holtan产流的分布式水文模型[J]. 河海大学学报自然科学版, 2016, 44(4): 340-346. |
| [35] |
叶金印, 李致家, 刘静, 等. 山洪灾害气象风险预警指标确定方法研究[J]. 暴雨灾害, 2016, 35(1): 25-30. DOI:10.3969/j.issn.1004-9045.2016.01.004 |
 2018, Vol. 37
2018, Vol. 37 
