2. 中国气象科学研究院灾害天气国家重点实验室,北京 100081
2. State Key Laboratory of Severe Weather, Chinese Academy of Meteorological Sciences, Beijing 100081
提高降水预报准确性一直是气象业务与科研工作的重点。然而,此项工作颇具困难和挑战性,因为降水是不同尺度天气系统相互影响的结果,其时空分布比较复杂,在不同时间尺度上其统计特征不同,如年降水量或季降水量可能服从正态分布[1],而日降水量或更短时间尺度内降水则呈偏态分布[2]。所以,对于降水的预报,用能描述降水出现可能性大小的形式即概率进行预报,较传统的确定性预报更有价值[3]。近年来,数值天气预报已逐渐从单值预报向多成员集合预报、从确定性预报向概率性预报转变。而集合预报则被认为是获得降水概率预报最有效的途径之一[4-5],并在国内得到了广泛应用。如:在洪水预报中,集合降水预报为山洪预报提供了多种定量预报产品[6];在短期降水预报中,陈静等[7]采用不同的参数化方案对我国的暴雨预报进行了研究与试验,其结果均表明集合预报对降水预报有重要影响。但由于数值模式和集合成员降水预报存在偏差,需要对降水集合预报进行偏差订正,从而在较多数值预报产品中提取更多有用的预报信息。
关于数值预报的订正,以往国内外学者采用方法较多,如模式输出统计法[8]、卡尔曼滤波方法[9]、频率匹配法[10]、统计降尺度法[11]、逻辑回归法[12-13]以及贝叶斯模型平均法(Bayesian Model Averaging,BMA)等;近年来,人们多采用BMA方法对集合预报进行偏差订正[14-17]。BMA方法是一种基于贝叶斯理论的、将模式本身的不确定性考虑在内的统计后处理方法,该方法可将不同来源的资料有机结合并最大限度地利用各模式的预报结果[18]。韩焱红等[19]利用贝叶斯产品处理器得到集成的贝叶斯降水概率预报,通过连续等级概率评分获知其可靠性高于由原始集合预报直接得到的概率预报结果。张宇彤等[20]基于模式先验信息的降水概率预报试验结果表明,相较集合预报结果,贝叶斯降水概率预报效果更好。杨赤等[21]根据多个预报中心的集合预报,利用BMA方法得到了降水概率预报,发现集合预报的中值可预报出大部分日期的降水状况,但不能提供极端降水信息。王玉虹[22]用BMA方法对ECMWF、UKMO和NCEP三个预报中心10~15 d的集合预报产品进行偏差订正,结果表明BMA方法能够比较准确地预报出小雨发生概率和降水量值以及大雨发生概率,但对大雨的降水量值预报存在一定偏差,并对无降水存在虚报。还有研究表明,BMA方法对微量降水和小雨的预报通常偏大,而对大雨的预报则偏小[23]。可见,虽然BMA方法对较小量级降水偏差订正有一定优势,但在大量级和极端降水上存在缺陷。
如何利用BMA方法的优势而避免其缺陷,从而达到对集合数值预报降水的订正目的呢?Krishnamurti等[24]研究表明,在季风影响期间,统计降尺度方法可有效地订正降水量级,使其与观测结果更接近。王海霞等[25]利用降尺度订正方法使模式的系统误差有明显的订正效果,并在逻辑回归的基础上采用降尺度方法进一步改善了模式预报的准确性,使预报值与实况值的相关度更高。统计降尺度方法可有效改善模式的原始预报效果,具有灵活多变、计算量相对较小等优点,已成为精细化预报中的一种重要订正方法[26]。
针对BMA方法对较大量级降水预报的订正能力有限的问题,如何获得合理可靠的降水预报,尤其是获得合理又可靠的较大降水预报,达到对集合数值预报降水的订正目的,是使用BMA方法要重点考虑的问题。这对提高大雨以上降水预报的订正效果具有重要的研究意义和业务应用价值。本文首先利用中国气象局国家气象中心(CMA)、欧洲中期天气预报中心(ECMWF)和美国国家环境预报中心(NCEP)三个全球数值预报业务中心(以下简称三个中心)的集合预报多成员的降水预报资料和国家级地面气象站逐小时历史降水观测资料,研究集合预报降水的BMA偏差订正与统计降尺度相结合的综合订正方法;然后,以我国降水事件发生较多的东南地区作为降水预报订正的试验和检验评估区域;最后,讨论该方法的局限性和应用前景。
1 研究区域、资料与方法 1.1 研究区域与资料说明本文的研究区域为我国东南地区(20°—35°N,100°—124°E)。该地区包含了我国受台风影响较为严重的浙江、福建和广东等省份,经常受到多种天气系统影响(图 1),天气多变,降水量级较大且容易发生极端降水事件。

|
图 1 我国东南地区及该区域内降水观测站(红点所示)分布 Fig. 1 Illustration of research area namely southeast China and the meteorological observation stations (red dots is shown in) in the region. |
集合预报资料为三个中心的集合预报系统在2015年6月1日—8月31日时段的24 h累积降水预报,起报时间为20:00 (北京时,下同),各模式集合预报系统的相关参数见表 1。降水观测资料为国家气象信息中心经过质量控制的国家级地面基准气象站整点观测的逐小时降水资料。为保证不同站点之间降水资料的一致性,剔除研究时段2015年6月1日—8月31日的缺测站点,得到研究区域内观测资料的站点数为1 263个(见图 1)。采用双线性插值的方法将格点预报降水插值到站点上,获得研究区域内站点24 h集合降水预报。由于BMA方法需要选择预报日期前25~30 d的降水预报作为建立BMA模型的训练样本,因此2015年6月的降水预报作为2015年7月20—26日个例试验的训练期资料,7月降水预报作为8月1— 31日批量试验的训练期资料。
|
|
表 1 三个数值预报中心的三套集合预报系统中的相关参数 Table 1 Several parameters of the three ensemble prediction systems from CMA, ECMWF and NCEP. |
BMA是一种基于贝叶斯理论的统计分析方法。最早是用多个统计模型进行联合推断和预测,Raftery等[27]将BMA方法用于服从正态分布的天气要素的集合预报后处理中,这样可以产生有预报效果的概率密度函数(Probability Density Function,PDF)。后被Sloughter等[28]推广到适用于集合降水概率预报。马培迎[29]通过将天气分为有、无降水来分别求出其期望概率作为先验概率,在此基础上应用贝叶斯原理对降水概率预报进行订正,提高了降水预报的准确性精度。设y为预报的天气要素“真实”值,fk是集合预报的第k个成员的原始预报值,f = f1, f2, …, fk分别表示集合预报k个成员的预报结果。hk(y|fk)表示当第k个成员的原始预报值fk为集合成员中的最佳预报时y所对应的一条正态PDF。因此,对于集合预报模型里的所有成员都有一个预报fk相对应的hk(y|fk),于是将各个成员的PDF加权就可得到整个集合预报预测的PDF:
| $ p\left( y|{{f}_{1}}, \cdots, {{f}_{k}} \right)=\sum\limits_{k=1}^{k}{{{\omega }_{k}}{{h}_{k}}\left( y|{{f}_{k}} \right)} $ | (1) |
其中,ωk代表第k个成员是最佳预报时的后验概率,其可以根据相应时段和区域的历史观测资料和历史预报资料计算得出。ωk始终大于0,且满足
降水尤其是日降水为非正态分布,并存在大量的零值,不能直接用正态分布的概率密度函数来描述其概率分布。因此要针对零降水量和非零降水量时的情况,采用不同的概率分布模型来分别构造条件概率分布密度函数。本文采用Sloughter等[28]的做法,即降水量发生的概率(P)采用Logistics模型:
| $ P\left( y=0|{{f}_{k}} \right)=\text{ln}\left[\frac{P\left( y=0|{{f}_{k}} \right)}{P\left( y>0|{{f}_{k}} \right)}={{a}_{0}}+{{a}_{1}}{{f}_{k}}^{\frac{1}{3}}+{{a}_{2}}{{\phi }_{k}} \right] $ | (2) |
其中ϕk为指示函数,当fk =0时,ϕk =1,其他情况ϕk =0。Gamma分布可用于非正态分布的降水量拟合,因此降水量为非零时采用Gamma分布模型来拟合降水概率密度分布,Gamma分布模型为:
| $ {{g}_{k}}\left( y|{{f}_{k}} \right)=\frac{1}{\beta _{k}^{{{\alpha }_{k}}}\mathit{\Gamma }\left( {{\alpha }_{k}} \right)}{{y}^{{{\alpha }_{k-1}}}}\text{exp}\left( -y|{{\beta }_{k}} \right), y>0 $ | (3) |
至此,将式(2)、(3)结合起来,hk(y|fk)可表示为:
| $ \begin{align} &{{h}_{k}}\left( y|{{f}_{k}} \right)=P\left( y=0|{{f}_{k}} \right)I\left[y=0 \right]+ \\ &\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ P\left( y>0|{{f}_{k}} \right){{g}_{k}}\left( y|{{f}_{k}} \right)I\left[y>0 \right] \\ \end{align} $ | (4) |
将式(4)代入式(1)中得到最终的降水集合预报PDF为:
| $ \begin{align} &p\left( y|{{f}_{1}}, \cdots, {{f}_{k}} \right)=\sum\limits_{k=1}^{k}{{{\omega }_{k}}}P\left( y=0|{{f}_{k}} \right)I\left[y=0 \right]+ \\ &\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ P\left( y>0|{{f}_{k}} \right){{g}_{k}}\left( y|{{f}_{k}} \right)I\left[y>0 \right] \\ \end{align} $ | (5) |
研究和业务中常用的降尺度方法,一般有动力降尺度方法和统计降尺度方法两种。动力降尺度是把大尺度、低分辨率数值模式输出信息转化为描述小尺度、高分辨率的气象预测信息的一种方法,统计降尺度则通过建立预报因子和预报对象之间的统计关系以获得预测信息的方法。前者一定程度上克服了统计方法的不足,但提高模式的分辨率会涉及到很多技术难题,且对计算条件要求也很高。而后者因其具有灵活多变、计算量相对较小等优点,应用更广泛[26]。本文采用一元线性回归统计降尺度模型,选取一定时间序列的训练期,建立模式预报值和实况观测值之间的统计关系[24]。统计方程如下:
| $ {{Y}_{i}}={{a}_{i}}{{X}_{i}}+{{b}_{i}} $ | (6) |
其中ai、bi为一元线性回归方程的系数,Xi为预报值,Yi为观测的实况降水资料。
本文利用公式(6)对三个中心和超级集合预报(即i = 1, 2, …, 4)分别建立统计降尺度模型(Yi),其中Xi为各中心和超级集合预报经BMA订正后第50百分位的降水预报值(可看作确定性预报),在一定长度的训练期内确定不同中心和超级集合预报的回归系数ai、bi后,利用式(6)对各模式的降水预报值进行降尺度订正。
1.2.3 BMA-统计降尺度方法本文在各中心和多模式超级集合预报进行BMA模型订正的基础上,利用各中心和多模式超级集合经BMA模型订正后的第50百分位降水预报(可看作确定性预报)与实况降水量,分别对各中心和多模式超级集合预报建立一元线性的统计降尺度模型。根据两种方法对降水预报进行二次订正,这样不仅能提高非正态分布降水预报的准确性,还能将订正后的降水预报值与实况观测值之间联系起来,避免因仅使用一种方法造成的空(漏)报率较高等问题,使其降水量级和落区预报更准确。为叙述简便,下文将贝叶斯模型平均订正方法简称A方案,将BMA-统计降尺度订正方法简称B方案。
1.2.4 预报检验方法TS评分(TS)是基于两分类常用的评分方法,其作为对确定性预报的评分指标已纳入确定性预报的评分体系中[30]。由于降水事件不是有就是无,所以TS评分是评估降水事件是否发生较好的度量指标,TS越大,表示预报评分越高。预报偏差(B)表示预报降水发生的次数和实况观测到降水发生的次数之比,当B =1时表明预报是无偏的,B>1时表示预报存在空报情况,而B<1时表示预报存在漏报情况,合理的B值结果一般在1~2之间。另外,概率性预报效果检验的方法有很多,本文选择三种概率性预报检验方法对各集合预报系统进行概率性降水预报检验。
(1) Brier评分。Brier评分(Brier score,BS)主要是对连续变量进行概率预报检验的一种指标。它在均方概率误差的基础上,还考虑到了概率预报的可靠性、分辨性和不确定性的特点[31]。BS计算公式为:
| $ {{B}_{\text{S}}}=\frac{1}{N}\sum\limits_{i=1}^{N}{{{\left( {{f}_{i}}-{{o}_{i}} \right)}^{2}}} $ | (7) |
其中fi是第i个样本事件发生的预报概率,其值在0~1之间。oi是第i个样本事件发生的观测频率,当观测到事件发生时,oi =1;当观测到的事件不发生时,oi =0。BS是负定向,且BS的数值在0~1之间,BS=0表示集合预报系统概率预报最佳,有完全准确的预报,其值越小表示集合预报系统的准确率越高。
(2) 连续等级概率评分。连续等级概率评分(continuous ranked probability score, CRPS)可以看作当阈值连续化后BS在所有可能阈值上的积分过程[21],它可以评估一个集合预报系统的整体性能。CRPS的计算公式为:
| $ CRPS={{\int_{-\infty }^{\infty }{\left[P\left( x \right)-{{P}_{a}}\left( x \right) \right]}}^{2}}\text{d}\mathit{x} $ | (8) |
其中,P和Pa分别表示集合概率预报和实况观测的累积分布,完美的预报CRPS值等于零,且该值越大,集合预报系统的预报能力越低。
(3) 平均绝对误差。平均绝对误差(Mean Absolute Error,EMA)表示各集合成员预报值与观测值偏离绝对值的平均,是一种比较直观的检验指标。EMA的计算公式为:
| $ {{E}_{\text{MA}}}=\frac{1}{N}\sum\nolimits_{i=1}^{N}{\left| {{f}_{i}}-{{x}_{i}} \right|} $ | (9) |
其中,N表示样本数,fi表示预报值,xi表示与之对应的观测值。对于原始集合预报,fi表示原集合平均值;对于BMA模型,fi表示各模式经订正后第50百分位降水预报值。EMA越小,表示预报值与观测值误差越小,预报能力越强。当预报值与观测值完全相等时,EMA=0,即为理想预报情况。
2 结果与分析 2.1 A方案对东南地区大范围降水过程的集合预报订正2015年7月全国强降水天气主要出现在我国南方,其中江南、华南、西南地区暴雨频繁,降水强度相对较大,南方大部地区降水量在100 mm以上[32]。分析2015年7月降水资料发现,7月20—26日研究区域多地产生持续性降水天气过程(图 2a),尤其是沿海地区降水普遍较大,7 d累积降水量在100~500 mm,其中23日是该过程降水量和降水范围均最大的一天(图 2b)。

|
图 2 2015年7月20—26日(a)和7月23日(b)我国东南地区各站点累积降水量分布(单位: mm) Fig. 2 The spatial distribution of accumulated precipitation (unit: mm) at each weather stations over southeast China (a) from July 20 to 26 in 2015 and (b) on 23 July 2015. |
首先,对比分析三个中心的集合预报以及由三个中心组成的超级集合预报(记为GE,下同)对2015年7月20—26日逐日降水预报经A方案订正前后的结果。经A方案订正后得到的是某个百分位的降水预报,第50百分位降水预报能够代表预报的平均状态。因此,采用第50百分位降水预报与降水观测进行不同中心和多模式超级集合预报订正前后的结果对比分析。表 2给出CMA、ECMWF和NCEP三个中心的集合预报和GE第50百分位预报的CRPS和MAE评分,以及A方案订正后的CRPS和MAE评分。结果表明,经A方案订正后各中心和GE集成预报的CRPS和MAE评分均明显小于原始集合预报(订正前,下同)的分值,说明经A方案订正后,各中心及GE预报的可靠性高于未订正集合预报;其中ECMWF原始集合预报的CRPS评分和MAE评分均值最小,而经A方案订正后,GE的CRPS评分和MAE评分均值最小。即在CRPS和MAE评分表现上,ECMWF原始集合预报的预报效果较好,而经A方案订正后,GE的预报效果较好。综上分析可知,BMA模型对GE的订正效果最佳。
|
|
表 2 2015年7月20—26日A方案订正前后各中心和GE集合预报第50百分位降水预报评分 Table 2 Continuous ranked probability score (CRPS) and mean absolute error (EMA) of the 50th percentile precipitation prediction from CMA, ECMWF, NCEP and GE (grand ensemble) at raw ensemble and after the correction by scheme A from July 20 to 26 in 2015. |
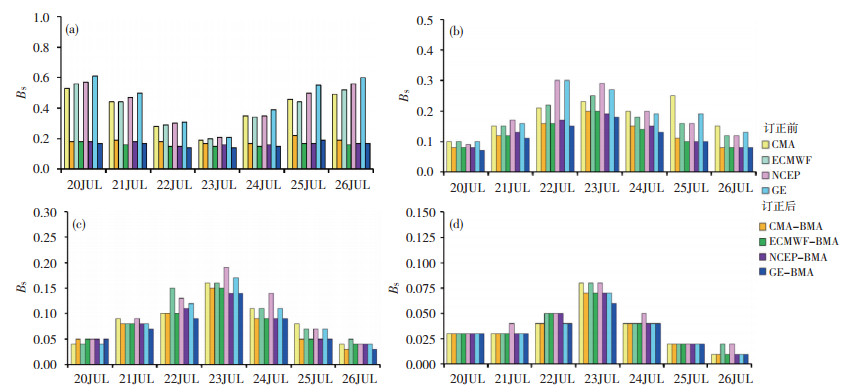
仔细考察A方案对各量级降水预报的订正效果(图 3)发现,在7月20—26日期间,对于0.1 mm阈值的降水预报,各中心和GE经A方案订正后的BS评分均小于集合方案预报的BS,其中除22日、23日集合和集成的BS差值在0.1左右外,其他时间BS差值都在0.3左右,说明A方案对阈值为0.1 mm降水的订正效果比较明显;对于10.0 mm阈值的降水预报,A方案对三个中心和GE均有订正效果,但没有降水阈值为0.1 mm时明显,值得注意的是,经A方案订正后,GE的10.0 mm阈值的降水预报BS比其他三个中心都低,说明A方案对GE订正效果明显;对于25.0 mm阈值的降水预报,A方案除对20日没有订正效果外,对其他时间都起到订正作用;对于50.0 mm阈值的降水预报,A方案除对23日和26日订正效果明显外,对其他日期订正效果均不为明显。总体看,A方案对于小雨、中雨的订正效果很明显,对于大雨有一定的订正,但对超过50.0 mm的降水订正效果不明显,且随着降水阈值增加,A方案的订正效果随之减弱。
|
图 3 2015年7月20—26日三个中心(CMA、ECMWF和NCEP)与GE各阈值(a. 0.1 mm;b. 10.0 mm;c. 25.0 mm;d. 50.0 mm)降水集合预报及其经A方案订正后的BS评分(BS) Fig. 3 The brier scores (BS) of the precipitation for ecast at the thresholds of (a) 0.1 mm, (b) 10.0 mm, (c) 25.0 mm and (d) 50.0 mm from the three centers (CMA, ECMWF and NCEP) and GE at raw ensemble and after the correction by scheme A from July 20 to 26 in 2015. |
由本文第2.1.1节的统计检验分析结果得知,A方案对中雨以下量级的降水预报订正效果明显,对大雨预报有一定的订正,但对暴雨以上量级的降水预报订正不明显。为了考察A方案对不同中心和多模式超级集合预报的订正效果,以第50百分位降水预报代表预报的平均状态,对其订正效果进行分析。以2015年7月23日为例详细说明如下。
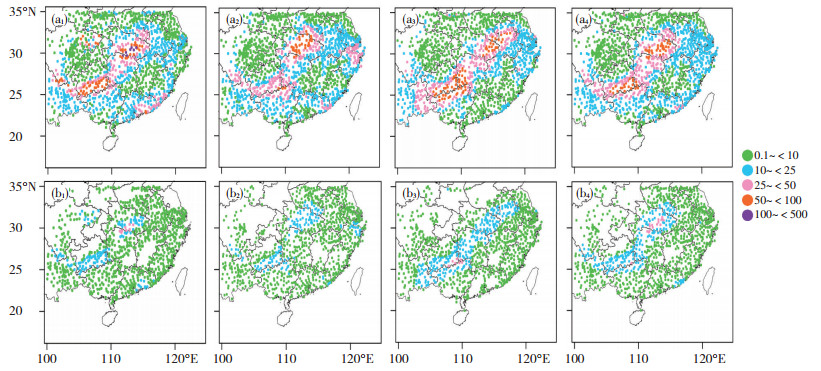
图 4为7月23日经A方案订正前后CMA、ECMWF、NCEP和GE的第50百分位的降水预报。7月23日(图 2b)东南大部分省份均有降水发生,在湖北、湖南到广西一带存在一条东北—西南向雨带,其大值中心位于湖北,最大24 h降雨量(414.5 mm)出现在湖北仙桃站。其中,当日广东东南部和广西大部降雨量为25.0~50.0 mm,广东东南沿海和广西西北部降雨量为50.0~100.0 mm,个别站点超过100.0 mm。其余地区降水量级为小雨。将上述各中心和GE原始集合预报(图 4a1-a4)与实况降水进行对比(图 2b)看出,当日三大中心和超级集合预报的原始集合预报小雨预报普遍存在较大的空报区域,如四川到重庆一带、山西南部到河南中部、湖南南部和江西南部以及江苏大部地区,没有降水发生,但各中心均预报了发生小雨(0.1~ 10.0 mm)的可能。此外,也存在量级预报偏大和偏小的区域,前者如对贵州南部到云南北部的小到中雨却报了大到暴雨量级,后者如对广西大部地区和广东沿海地区50.0~100.0 mm降水量级却只报了10.0~25.0 mm量级。而对湖北降水大值中心,只有CMA预报了发生100.0 mm以上降水的可能。
|
图 4 2015年7月23日三个中心(CMA、ECMWF和NCEP)及GE集合预报经A方案订正前后第50百分位的降水(单位: mm)预报(a1—a4分别为CMA、ECMWF、NCEP和GE原始集合预报;b1—b4分别为订正后的降水预报) Fig. 4 The 50th percentile precipitation prediction (unit: mm) from (a1, b1) CMA, (a2, b2) ECMWF and (a3, b3) NCEP, and (a4, b4) GE (a1-a4) at raw ensemble and (b1-b4) after the correction by scheme A on 23 July 2015. |
同时,A方案对各中心以及GE降水预报的空报率的订正效果(图 4b1-b4)非常明显,消除了各中心和GE原始集合预报在江西、陕西南部到河南中西部以及四川、重庆一带的降水空报。经A方案订正后的第50百分位降水发生的分布与实况降水分布更接近,各中心和GE均报出存在于湖北、湖南到贵州一带的东北—西南向雨量带,其中CMA和GE还报出湖北降水大值中心,NCEP报出广西与贵州交界处的降水大值中心,但经A方案订正后的雨带和大值中心其降水量级明显偏低。当各中心和GE集合降水预报的第50百分位降水在10.0~25.0 mm之间时,经A方案订正后的第50百分位降水量都在0.1~10.0 mm之间;当集合降水预报的第50百分位降水超过25.0 mm甚至超过50.0 mm时,经A方案订正后的第50百分位降水量都在10.0~25.0 mm之间。这与第2.1.1节中的统计检验得到的结论一致。但经A方案订正后各中心对广西或广东南部沿海等地区实况发生的大值降水预报并无改善,究其原因,可能是A方案订正后的结果依然与集合预报原始预报结果密切相关,原始集合预报结果不准确造成经A方案订正后降水预报不准确,且本文在此分析的是订正后第50百分位降水预报,其不能提供某些极端降水事件的信息。因此,下文在此基础上根据A方案订正后结果与实况降水量之间的关系建立一元线性方程,以期提高大值降水预报的准确性。
总体看,经A方案订正后,各中心和GE集合预报均消除了大量的空报,但雨带走向订正不明显。A方案仅能较为准确地预报出小雨发生的概率和降水量值,对中雨也有一定的订正能力,但对中雨以上更大量级降水的订正能力有限,因降水量级预报偏小,使得主要雨带预报不明显,且使得降水大值区量级降低甚至消失。如何在A方案消除空报的基础上又能保证降水的雨带降水量级预报合理、降水的极值中心降雨量级预报正确呢?最可取的办法是在A方案订正的基础上对集合预报降水进行二次订正。
2.2 东南地区大范围降水过程的集合预报综合订正由第2.1节中的统计检验和对7月23日降水预报的具体分析得知,A方案对各中心和多模式超级集合预报的空报有显著的订正效果,但其对较大量级降水的量级订正偏低甚至出现漏报,导致降水大值区域不明显,大值中心不突出,因此,需对各中心和GE的BMA集成结果进行二次订正(B方案)。表 3给出2015年7月20—26日不同降水阈值三个集合预报中心和GE原始集合预报、A方案和B方案订正后第50百分位预报的统计检验。
|
|
表 3 2015年7月20—26日三个中心(CMA、ECMWF、NCEP)与GE的原始集合预报及其经A方案和B方案订正后第50百分位降水(4个阈值)预报的TS评分(Ts)与预报偏差(B) Table 3 Threaten scores (Ts) and bias (B) of the 50th percentile recipitation (at 4 thresholds) prediction from CMA, ECMWF and NCEP, and GE at raw ensemble and after the correction by scheme A and scheme B from July 20 to 26 in 2015. |
从表 3中看到,在降水阈值为0.1mm时,B方案订正后的评分与A方案的评分结果相当,但在0.1mm以上阈值各中心和GE经B方案订正后的TS评分高于A方案订正,预报偏差(B) B方案要比A方案订正的结果更接近于1。B方案订正后各降水阈值预报评分明显提高。在此研究时段内对比各中心和GE的评分,未经订正的原始集合预报在降水阈值为0.1 mm时各中心和GE的TS相当,但在降水阈值为10.0 mm时GE的TS最大,而随着降水阈值增加,CMA原始集合预报在降水阈值为25.0 mm和50.0 mm时TS评分最大,而经A方案和B方案订正后各阈值下均是GE的TS最大,B最接近于1,即GE经各方案订正后对降水量级的预报效果最好。总体上,GE原始集合预报对稍小降水量级预报比较准确,CMA原始集合预报对稍大降水量级预报比较准确。而经A方案和B方案订正后GE对降水量级的预报效果最好。也就是说,经订正后相比单中心预报多模式集成预报的预报质量较好,这种现象在前人有关地面气温和降水的多模式集成预报中也有类似表现[33]。
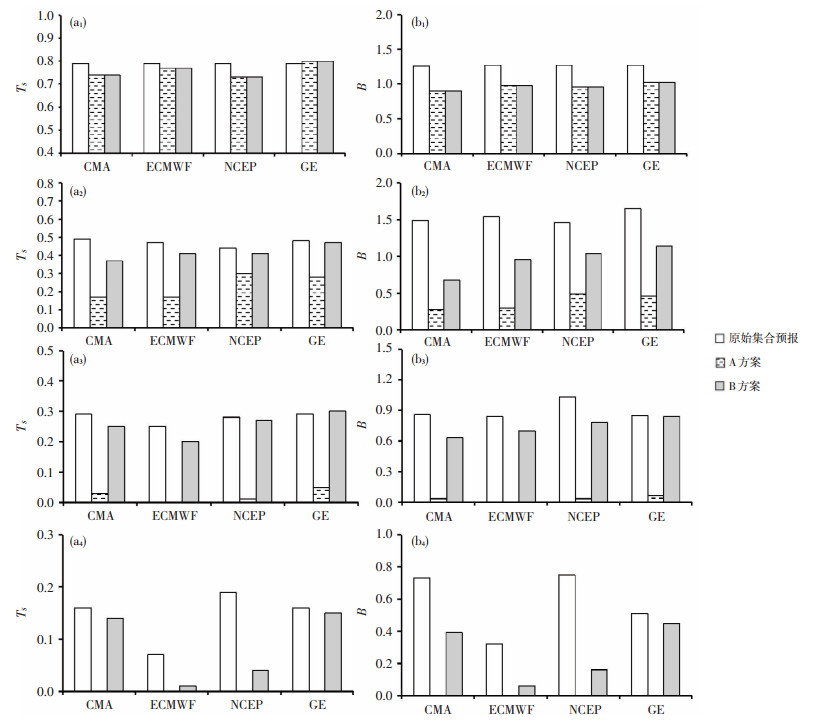
选取研究时段内的7月23日进行具体分析。图 5给出2015年7月23日三个中心和GE集合预报第50百分位、经A方案和B方案订正后第50百分位不同降水阈值预报的TS和B。对于阈值为0.1 mm的降水预报,当日单中心原始集合预报的TS高于订正后的,其原因可从图 5b1中找到,即单中心原始集合预报的B值在1.5附近,说明各中心对降水预报有较高的空报,造成原始集合预报TS较大。GE经A方案和B方案订正后的TS高于原始集合预报,说明GE的预报效果最好。而降水阈值为0.1 mm的B值(图 5b1)表明,A方案集成预报和B方案集成预报的值均在1.0附近,这很大程度降低了各中心集合预报的空报率;对于降水阈值为10.0 mm和25.0 mm的降水预报,各集合预报和B方案集成预报的TS (图 5a2-a3)和B (图 5b2-b3)均大于A方案集成预报的,对比各中心和GE集合预报与BMA-降尺度集成预报的评分结果,其中多模式超级集合预报的BMA-降尺度集成预报TS最大,B最接近于1.0,订正效果最好。由此可知,B方案订正后的降水预报结果在阈值为10.0 mm和25.0 mm下要好于只经A方案订正的结果,说明B方案订正对于中雨和大雨降水预报结果订正效果明显,有订正意义;对于阈值为50.0 mm的降水预报,各中心和GE原始集合预报的TS(图 5a4)和B (图 5b4)大于A方案集成预报和B方案集成预报,原始集合预报效果最好。但B方案集成预报的TS和B大于A方案集成预报,说明在A方案集成预报基础上进行降尺度订正后集成预报对于暴雨的订正也有一定效果。综上所述,B方案对三个中心和GE在小雨以上量级降水预报结果有较好的订正效果,其中多模式超级集合预报的预报效果最好。
|
图 5 2015年7月23日三个中心(CMA、ECMWF和NCEP)及GE的原始集合预报以及A方案和B方案的第50百分位集合预报降水的TS评分(TS)与预报偏差(B) (a1-a4分别为降水阈值0.1、10.0、25.0、50.0mm的TS;b1-b4分别为降水阈值0.1、10.0、25.0、50.0mm的B) Fig. 5 (a1-a4) Threaten scores (TS) and (b1-b4) bias (B) of prediction of the 50th percentile precipitation at thresholds of (a1, b1) 0.1 mm, (a2, b2) 10.0 mm, (a3, b3) 25.0 mm and (a4, b4) 50.0 mm from CMA, ECMWF and NCEP, and GE at raw ensemble and after the correction by scheme A and scheme B on 23 July 2015. |
图 6给出三个中心和GE在2015年7月23日经B方案订正后的降水预报。从中看出,B方案订正后可进一步改善各中心和GE集合预报降水的强度。三个中心(图 6a-c)和GE (图 6d)集合预报对位于湖北、湖南到广西的东北-西南向强降水雨带的量级得到了很大订正,即由0.1~10.0 mm订正到了25.0~50.0 mm甚至100.0 mm, 与A方案(图 4b1-b4)相比其与实况更接近。但三个中心和GE集合预报对位于广西的强降水雨带预报落区偏西北。究其原因,这与各中心原始集合预报(图 4a1-a4)有密切关系,三个中心及GE原始集合预报对广西降水落区预报均偏西北,对比各中心和GE发现,各自的雨区形状或走向在订正前后变化不大,表明使用该方法不能改进雨区位置的预报。此外,将A方案订正后与B方案订正后对比发现,B方案订正后各中心和GE的降水预报落区与量级与实况较为接近,其中GE最接近,订正效果更好,与表 3统计检验结果所得结论一致。

|
图 6 2015年7月23日CMA (a)、ECMWF (b)、NCEP (c)中心与GE (d)集合预报经B方案订正后第50百分位的降水预报(单位: mm) Fig. 6 The 50th percentile ensemble precipitation prediction (unit: mm) from (a) CMA, (b) ECMWF, (c) NCEP, and (d) GE after the correction by scheme B on 23 July 2015. |
从2015年7月20-26日订正试验看出,A方案对空报有消除作用但降低了降水的量级;B方案对强降水中心量级和落区订正作用较明显,雨区的范围和强度与实况更接近。因此,采用A方案订正后再进行降尺度订正不仅可将原始集合预报的空报率降低,还可订正降水量级和落区,使降水预报的范围和量级与实况更接近。这较好地解决了原始集合预报空报多、降水预报量级偏大的问题,同时也修正了单纯A方案订正对较大降水量级偏低甚至漏报等问题,使三个中心和GE集合降水预报得到合理可靠订正。
2.3 独立样本的东南地区降水集合预报综合订正为进一步验证本文订正方案的预报效果,选取2015年8月1-31日三个中心及GE集合预报24 h集合预报进行独立样本预报试验。早在2009年Krishnamurti等[24]就提出多模式超级集合预报可有效减少天气预报的误差,预报效果要优于单个模式预报,智协飞等人[33]利用TIGGE资料对5个中心的降水集合预报结果进行集成预报,结果表明多模式集成的预报效果好于单个中心的降水预报。本文第2.1节的统计检验(表 2)和预报效果分析(图 4)表明: A方案对三个中心集合预报均有订正,且多模式超级集合预报的订正程度最大。因此,B方案的批量试验就基于多模式超级集合预报来进行。
从2015年8月1-31日超级集合预报经A方案订正后第50百分位降水预报的CRPS和MAE评分可看出,经A方案订正后的CRPS评分和MAE评分值均明显小于原始集合预报的评分(图略),说明经方案A订正的超级集合预报的准确性高于原始集合预报。不同阈值下GE的原始集合和经A方案订正后的降水预报BS评分,对于0.1 mm阈值的降水预报,GE超级集合预报经A方案订正后的BS明显小于原始GE集合预报的,A方案订正后将BS降低0.4左右,说明A方案对降水阈值为0.1 mm的订正效果较明显;对于10.0 mm阈值的降水预报,A方案超级集合预报也有订正效果,但没有降水阈值为0.1 mm时的明显;对于25.0 mm和50.0 mm阈值的降水概率预报,A方案对超级集合预报订正效果几乎没有。总体看,A方案对于小雨、中雨的订正效果很明显,对于大雨以上订正效果不明显,随着降水阈值增加,A方案的订正效果随之减弱。
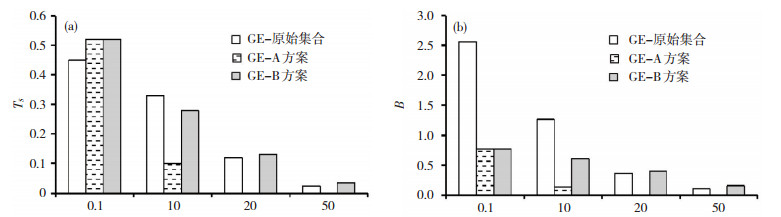
图 7为采用B方案对超级集合预报GE订正不同降水阈值31 d降水第50百分位预报的TS(图 7a)和B (图 7b)。对于阈值为0.1 mm的小雨量级降水,A方案与B方案订正的TS比原始集合预报的明显增加,且订正后的B更接近1.0,说明两种方法对小量级降水的订正效果明显,且两者相差不大。降水阈为10.0 mm时,B方案订正后的TS虽然小于原始集合预报,但与A方案相比大大缩小了与原始预报TS的差距,但在降水阈值为25.0 mm时,B方案订正后的TS得到较大提高,且B值比GE原始集合更接近1.0;而降水阈值为50.0 mm时,TS也获得了提高,且B值比GE原始集合更接近1.0。、
|
图 7 2015年8月1-31日GE原始集合预报及其经A、B方案订正后第50百分位各阈值降水预报的TS评分(a)和偏差(B) Fig. 7 (a) Threaten scores (TS) and (b) bias (B) of prediction of the 50th percentile precipitation at different thresholds from GE at raw ensemble and after the correction by scheme A and scheme B from 1 to 31 August 2015. |
综合TS和B值表现看出,B方案明显大于A方案的订正效果,说明在A方案订正的基础上再进行降尺度订正其效果较好,从而说明BMA模型具有能减小空报的优势,而降尺度方法能提高大雨和暴雨的预报准确率。因此,采用BMA模型和降尺度法相结合的订正方法不仅可以改善小雨空报,对大雨以上量级降水集合预报的降水强度也有很大改善,这两种方法的结合,可实现对集合数值预报不同降水量级订正的目的。
3 小结与讨论本文将贝叶斯模型平均方法(A方案)和基于贝叶斯模型平均方法的降尺度模型订正方法(B方案)用于我国东南地区降水集合预报误差订正,分析比较了CMA、ECMWF和NCEP三个中心的降水集合预报与多中心超级集合预报误差订正效果。主要结论如下:
(1) 各中心和多模式原始集合预报存在小雨空报、大雨漏报现象,经A方案订正后,多模式超级集合预报的订正效果最好。以第50百分位降水预报为例: BMA偏差订正后各中心和多模式的集合平均消除了大量的小雨空报,对小雨、中雨订正效果很明显;对大雨有一定订正效果,但对超过50.0 mm的降水量级订正效果不明显。A方案因使降水量级预报偏小、主要雨带不明显,造成对雨带走向订正不显著、降水大值区量级降低甚至消失。
(2) B方案订正后的降水预报结果在阈值为10.0 mm和25.0 mm以下要好于只经A方案订正的结果,B方案订正对于中雨和大雨降水预报结果的订正效果明显,有订正意义;对阈值为50.0mm的降水预报,B方案比A方案订正效果好,但相比原始集合预报没有明显改善。
(3) BMA模型具有能减小空报的优势,而BMA-降尺度方法相比BMA方法能提高稍大降水量级的预报准确率。因此,采用B方案的订正方法不仅可降低原始集合预报的空报率,还可对降水量级和落区进行订正,使降水预报的范围和量级与实况更接近。这不仅较好地解决了原始集合预报小雨空报多、降水预报量级偏大的问题,也修正了单纯A方案订正对较大降水量级偏低甚至漏报等问题,使三个中心和GE集合得到了合理可靠的降水预报订正,其中对GE的订正效果最好。
(4) B方案订正后的降水预报仍然存在空报和漏报等情况,尤其对大量级和极端降水预报不准确,且各中心和GE各自的雨区形状或走向在订正前后变化不大。这表明该方法对雨区的位置和极端降水预报的改进效果不明显,其结果与原始集合预报密切相关,对其改进更需要依赖模式自身能力的提高、物理过程的改进等,消除原始集合预报模式的系统误差。需要说明的是,BMA本质上是一种统计方法,对某一特定变量经过偏差校正的单个模型概率预报的加权平均,其权重是相应模型的后验概率,代表着每个模型在训练期相对的预报技巧。它必须基于观测资料对模型中参与集合的各个预报模型进行训练,测试以确定其权重系数。在训练的过程中对参加训练数据的选取至关重要。此外,训练期的长度也具有时间性和区域性,需要经验和不断试验才能获得最佳的预报效果。由于该方法对观测资料的依赖性,使得其应用也存在一定的局限性。虽然BMA能够包含模式的历史信息,但仍存在空报和漏报。而一元线性回归统计降尺度模型则具有灵活多变、降低或消除空报、计算量小等优势。两种方法结合,可达到优势互补的效果。
需要指出的是: (1)本研究过程中仅讨论了第50百分位的24 h降水预报,其他预报时效和其余百分位预报未多涉及,因此如何基于更多概率预报捕捉更多更有用信息以减少空报漏报,这是今后研究的方向。(2)集合预报降水的误差来源较多,本文贝叶斯模型平均法以及降尺度模型订正主要用于减小模式预报误差,但订正效果受模式系统误差影响,如雨带位置的误差影响。(3)站点预报资料采用双线性插值方法得到,插值过程中未考虑地形等因素影响,对降水预报评估也未考虑这种影响。(4)对于降水量级和降水落区预报偏差的订正方法,有待今后进一步探索和试验,如分级降尺度订正法、采用与不同的降水类型或不同的天气形势系统进行结合的方法等。
| [1] |
丁裕国. 降水量Γ分布模式的普适性研究[J]. 大气科学, 1994, 18(5): 552-560. DOI:10.3878/j.issn.1006-9895.1994.05.05 |
| [2] |
Wilks D S. Maximum Likelihood Estimation for the Gamma Distribution Using Data Containing Zeros[J]. Journal of Climate, 1990, 3(12): 1 495-1 501. DOI:10.1175/1520-0442(1990)003<1495:MLEFTG>2.0.CO;2 |
| [3] |
林春泽, 祁海霞, 智协飞, 等. 中国夏季降水多模式集成概率预报研究[J]. 暴雨灾害, 2013, 32(04): 354-359. |
| [4] |
陈静, 陈德辉, 颜宏. 集合数值预报发展与研究进展[J]. 应用气象学报, 2002, 13(4): 497-507. DOI:10.3969/j.issn.1001-7313.2002.04.013 |
| [5] |
矫梅燕. 天气业务的现代化发展[J]. 气象, 2010, 36(7): 1-4. |
| [6] |
李俊, 廖移山, 张兵, 等. 集合数值预报方法在山洪预报中的初步应用[J]. 高原气象, 2007, 26(4): 854-861. |
| [7] |
陈静, 薛纪善, 颜宏. 华南中尺度暴雨数值预报的不确定性与集合预报试验[J]. 气象学报, 2003, 61(4): 432-446. DOI:10.3321/j.issn:0577-6619.2003.04.005 |
| [8] |
Glahn H R, Lowry D A. The Use of Model Output Statistics (MOS) in Objective Weather Forecasting[J]. Journal of Applied Meteorology, 1972, 11(8): 1 203-1 211. DOI:10.1175/1520-0450(1972)011<1203:TUOMOS>2.0.CO;2 |
| [9] |
马旭林, 时洋, 和杰, 等. 基于卡尔曼滤波递减平均算法的集合预报综合偏差订正[J]. 气象学报, 2015, 73(5): 952-964. |
| [10] |
李俊, 杜钧, 陈超君, 等. 频率匹配法"在集合降水预报中的应用研究[J]. 气象, 2015, 41(6): 674-684. DOI:10.3969/j.issn.1000-6362.2015.06.003 |
| [11] |
智协飞, 王姝苏, 周红梅, 等. 我国地面降水的分级回归统计降尺度预报研究[J]. 大气科学学报, 2016, 39(3): 329-338. |
| [12] |
Applequist S, Gahrs G E, Pfeffer R L, et al. Comparison of methodologies for probabilistic quantitative precipitation forecasting[J]. Weather and Forecasting, 2002(17): 783-799. |
| [13] |
赵琳娜, 董航宇, 吴亮, 等. 黄淮地区夏季日降水分区概率预报方法研究[J]. 气象, 2015, 41(12): 1 503-1 513. |
| [14] |
Wilson L J, Beauregard S, Raftery A E, et al. Calibrated surface temperature forecasts from the Canadian ensemble prediction system using Bayesian model averaging[J]. Monthly Weather Review, 2005, 135(4): 4 226-4 230. |
| [15] |
Sloughter J M, Gneiting T, Raftery A E. Probabilistic wind speed forecasting using ensembles and Bayesian model averaging[J]. J Am Stat Assoc, 2010, 105(489): 25-35. DOI:10.1198/jasa.2009.ap08615 |
| [16] |
Yang C, Yan Z W, Shao Y H. Probabilistic Precipitation Forecasting Based on Ensemble Output Using Generalized Additive Models and Bayesian Model Averaging[J]. Journal of Meteorological Research, 2012, 26(1): 1-12. |
| [17] |
智协飞, 李刚, 彭婷. 基于贝叶斯理论的单站地面气温的概率预报研究[J]. 大气科学学报, 2014, 37(6): 740-748. |
| [18] |
Duan Q, Ajami N K, Gao X, et al. Multi-model ensemble hydrologic prediction using Bayesian model averaging[J]. Advances in Water Resources, 2007, 30(5): 1 371-1 386. DOI:10.1016/j.advwatres.2006.11.014 |
| [19] |
韩焱红, 矫梅燕, 陈静, 等. 基于贝叶斯理论的集合降水概率预报方法研究[J]. 气象, 2013, 39(1): 1-10. |
| [20] |
张宇彤, 矫梅燕, 陈静. 基于模式先验信息的贝叶斯集合降水概率预报试验[J]. 气象, 2013, 39(10): 1 233-1 246. |
| [21] |
杨赤, 严中伟, 邵月红.基于TIGGE集合预报的概率定量降水预报[A]//变化环境下的水资源响应与可持续利用--中国水利学会水资源专业委员会2009学术年会.大连: [出版者不详], 2009: 682-689 http://cpfd.cnki.com.cn/Article/CPFDTOTAL-ZGSL200912001118.htm
|
| [22] |
王玉虹.基于BMA方法的地面气温和降水的延伸期概率预报研究[D].南京: 南京信息工程大学, 2016 http://cdmd.cnki.com.cn/Article/CDMD-10300-1016197944.htm
|
| [23] |
彭婷.基于贝叶斯模式平均的东亚地区的气温和降水的概率预报[D].南京: 南京信息工程大学, 2013 http://cdmd.cnki.com.cn/Article/CDMD-10300-1013340463.htm
|
| [24] |
Krishnamurti T N, Mishra A K, Chakraborty A, et al. Improving Global Model Precipitation Forecasts over India Using Downscaling and the FSU Superensemble. Part Ⅰ: 1-5-Day Forecasts[J]. Monthly Weather Review, 2009, 137(137): 2 736-2 757. |
| [25] |
王海霞, 智协飞. 基于TIGGE多模式降水量预报的统计降尺度研究[J]. 气象科学, 2015, 35(4): 430-437. |
| [26] |
黄刚, 张立凤, 王秋良, 等. 基于集合预报产品的降尺度降水预报试验[J]. 气象科学, 2012, 32(5): 508-514. DOI:10.3969/2012jms.0065 |
| [27] |
Raftery A E, Gneiting T, Balabdaoui F, et al. Using Bayesian Model Averaging to Calibrate Forecast Ensembles[J]. Monthly Weather Review, 2005, 133(5): 1 155-1 174. DOI:10.1175/MWR2906.1 |
| [28] |
Sloughter J M, Raftery A E, Gneiting T, et al. Probabilistic Quantitative Precipitation Forecasting Using Bayesian Model Averaging[J]. Monthly Weather Review, 2007, 135(9): 3 209-3 220. DOI:10.1175/MWR3441.1 |
| [29] |
马培迎. 应用贝叶斯原理修正降水概率预报[J]. 气象科技, 1999(1): 45-48. |
| [30] |
黄嘉佑.气象预报产品质量评分系统技术手册[G].北京: 中国气象局预测减灾司, 2001: 9-11
|
| [31] |
赵琳娜, 吴昊, 田付友, 等. 基于TIGGE资料的流域概率性降水预报评估[J]. 气象, 2010, 36(7): 133-142. |
| [32] |
沈晓琳, 张芳华, 周博坤. 2015年7月大气环流和天气分析[J]. 气象, 2015, 41(10): 1 298-1 304. |
| [33] |
智协飞, 季晓东, 张璟, 等. 基于TIGGE资料的地面气温和降水的多模式集成预报[J]. 大气科学学报, 2013, 36(3): 257-266. DOI:10.3969/j.issn.1674-7097.2013.03.001 |
 2017, Vol. 36
2017, Vol. 36 
