2. 国网浙江省电力公司,杭州 310001;
3. 国网浙江省电力公司台州供电公司,台州 318000
2. State Grid Zhejiang Electric Power Company, Hangzhou 310001;
3. State Grid Taizhou Electric Power Company, Taizhou 318000
输电线路覆冰是引起电网事故的主要自然灾害之一,一旦发生可造成巨大社会经济损失。随着电网建设规模不断扩大,越来越多的输电线路走廊出现在覆冰易发的丘陵和山区[1]。而雨雪冰冻灾害受环流异常影响[2, 3],在当前气候变化背景下雾凇和湿雪天气的强度有增大趋势[4],未来电网覆冰灾害或将加剧,客观准确的覆冰灾害风险评估对风险管理和防灾减灾尤为重要。浙江省位于我国东部沿海,气候温暖湿润,历史记载的输电线路覆冰灾害不多[5],但近年极端冰冻天气频率加大,给经济承载量巨大的电力系统造成了严重影响。2008年1—2月雨雪冰冻灾害,致使浙江省341个乡镇、8 756个村和183.6万用户停电,直接经济损失高达27.5亿元[6]。以浙江省为例开展输电线路覆冰灾害风险评估具有重要的实用价值和借鉴意义。
目前国内输电线路覆冰风险评估方法体系尚待完善。就风险定义而言,风险是与某种不利事件有关的一种未来情景[7],其不仅是对灾难的统计结果,更是对未来不利事件情景不确定性的描述。然而,以往覆冰灾害风险研究多侧重单次灾害中的损失或危险程度,如灾害导致供电企业的经济损失[8, 9]、线路覆冰闪络跳闸风险等级[10]等,而从输电线路灾害发生不确定性或电网失效可能性方面的研究较少。就风险评估发展历程来看,作为风险评估重要方面的致灾因子评估乞今至少经历了极值化阶段、平均阶段和超越概率阶段3个阶段[11, 12]。国外冰区分布图开始利用覆冰模型等拓展历史覆冰极值数据的长度[13, 14],利用超越概率方法绘制冰区重现期。虽然国内对覆冰灾害也研究颇多,但受历史覆冰观测站点少且分布不均、数据缺测等限制,省级冰区分布图的绘制仍多处于平均阶段[15-18],从方法的复杂性和科学性而言,较超越概率评估还有一定差距。
综上,本文将输电线路覆冰灾害的风险定义为覆冰电网失效的可能性。首先,根据区域灾害系统理论,探索基于超越概率方法评估输电线路覆冰灾害风险的方法流程。其次,以浙江省为例,通过引入覆冰生成数值模式反演历史覆冰灾害进行致灾因子评估,并进一步结合输电线路属性资料、电网运行记录、地形等资料,选取输电线路易损性模型,评估杆塔尺度的浙江省输电线路覆冰灾害风险。最后,对评估方法及结果进行评价总结,以期为浙江省覆冰灾害风险管理提供依据,为方法的推广适用提供参考。
1 资料及预处理本文使用的资料有4类。
(1) 致灾因子数据。1)浙江省气象局提供的站点观测数据,选取浙江及周边省份2005—2014年冬季(11月—次年3月,下同)常规站每6 h、自动站每1 h的降水、风速、温度、相对湿度和气压数据,基于趋势面、反距离、线性回归等经典方法,插值为0.01°× 0.01°分辨率栅格数据。2)美国国家环境预测中心(NCEP) FNL再分析逐日资料,选取2005—2014年冬季350—1 000 hPa、1 °×1 °分辨率逐6 h的温度、湿度数据。
(2) 承灾体数据。浙江省电力公司提供的电网杆塔属性数据,字段包括杆塔编号、电压等级、位置、海拔、类型、回路数、采集时间、是否耐张等。数据部分记录缺失。为方便后续统计分析,增加利用0.01°×0.01°分辨率数字地形海拔数据(DEM)提取的杆塔海拔(以下简称0.01 d DEM)、与相邻杆塔的相对海拔、气候指数指标等字段。
(3) 灾情案例数据。1) 2008年冰灾期间浙江省覆冰倒塔事故点数据,共239条记录,属性字段包括杆塔经度、纬度、所属线路、倒塔时间。2) 2008年冰灾期间浙江省电网故障段勘察数据,共46条记录,属性字段包括电压等级、线路名称、故障段平均海拔、故障段所处地域、故障段导线直径、故障段设计覆冰、实测覆冰最厚处冰厚、覆冰性状、覆冰类型比重、标准比重的冰厚等。3) 2013年冰灾期间宁波地区电网故障段勘察数据,共21条记录,属性字段同数据2)。以上数据均由浙江省电力公司提供。
(4) 基础地理数据。0.01°×0.01°分辨率DEM数据,由美国航天局(NASA)与日本经济产业省(METI)共同推出ASTER GDEM数据集重采样得到,该数据主要用于覆冰生成模式。
2 方法 2.1 致灾因子危险性评估本节将探索利用超越概率的方法,开展输电线路覆冰灾害危险性评估的流程,并通过绘制冰区图来呈现评估结果。超越概率阶段致灾因子危险性评估的主要思路是:首先估计限定时段内研究区超越某一强度参数的概率分布,然后选定一个概率水平值作为阈值,以超越此水平的强度作为危险性对致灾因子进行描述。
2.1.1 历史覆冰灾害过程重建准确刻画致灾因子概率分布需要大量样本,而灾害事件往往具有频率低、损失大的特点,覆冰观测资料缺乏,成为冰区图绘制的主要困难。常规气象站大多在城镇附近,往往距线路远、海拔低,很难反映线路覆冰的实际情况;高山气象站,虽海拔多在千米以上,但数量较少且存在年代观测缺失,以浙江为例目前仅存2个高山气象站资料。以上两者受限于时空分辨率,通常难以监测或评估输电线路覆冰,更难以及时获取灾害时刻的覆冰极值。2004年以来,自动气象站密集布设并开始常规发布1 h气象数据,从时空分辨率上对常规站的观测起到了很大补充,能为覆冰概率分布计算提供更为真实有效的数据基础,但离散自动站观测并不能完全满足输电线路覆冰灾害监测需求。
为此,拟充分利用现有观测数据,通过引入数值模式重建历史覆冰灾害过程来解决样本不足的问题。首先,基于常规站及自动站气象数据,选取适当覆冰生成数值模式,针对历史冬季覆冰灾害时段,进行研究区面域栅格尺度的覆冰厚度模拟。其次,进行覆冰厚度降尺度研究,将栅格尺度覆冰厚度模拟结果转化为输电线路杆塔尺度的覆冰厚度,重建输电线路灾害覆冰过程。
2.1.2 致灾因子强度概率分布估算及冰区图绘制基于上述覆冰厚度模拟结果,选取致灾因子强度表征量,进而通过以下统计方法建立该要素概率分布。本文利用单场覆冰过程中各时次覆冰厚度最大值表征致灾因子强度。
首先,选取研究区适合致灾强度表征量的概率统计模型。研究发现,极值Ⅰ型分布的拟合效果较好,且有冰厚极值小于极值Ⅱ型和P-Ⅲ型分布的计算结果[18, 19],故覆冰厚度概率分布拟合选取经典极值I型,即Gumbel分布,其函数[20]如式(1)所示。其次,利用年最大抽样法(AM),选取冬季各年年最大覆冰厚度样本。然后,利用矩估计法进行参数估计。根据式(2)得到Gumbel函数的2个参数[20],进而代入式(1),即可得到覆冰厚度概率密度分布参数。最后,基于致灾因子强度概率分布,结合分布函数的意义和其与重现期的关系,可得式(3)。需注意的是,重现期是一种概率意义上的表达,n年一遇表示以年为单位统计上具有n分之一发生的可能性,但实际可能n年内发生超过一次或不发生。
| $ F(x) = P(X < x) = {\rm{exp}}[-{\rm{exp}}(-\alpha (x-u))]\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; - \infty < x < \infty $ | (1) |
| $ \left\{ \begin{array}{l} \hat a = \frac{{\rm{ \mathsf{ π} }}}{{\sqrt 6 }}\frac{1}{{{\sigma _M}}}\\ \hat u = {\mu _M}-c\frac{{\rm{ \mathsf{ π} }}}{{\sqrt 6 }}{\sigma _M} \end{array} \right. $ | (2) |
式(2)中,μM代表极大值样本的期望值,σM代表极大值样本的标准差,c = 0.577 2为欧拉常数。
| $ [1-F(x)] \cdot m = P(X \ge x) = \frac{1}{T} $ | (3) |
式(3)中,T为以年为单位的重现期,m为每年发生的事件次数(AM抽样方法m取1)。
2.2 承灾体易损性评估易损性模型通常需要以大量的实际调查或工程试验数据为依托,建立致灾因子强度与灾害损失可能性之间的关系。然而,一方面,输电线路灾情复杂[21],而详细记载覆冰灾情的资料相对不足;另一方面,输电线路损坏与气象因素、地形因素、布设方式、自身属性等有关[22],单一路段线路可以通过固定要素建立单变量或多变量的易损性模型,但对于省域电网来说,通过工程试验建立涉及多维的易损性物理模型较为困难。
为寻求相对简便而客观科学的易损性评价方案,本文假设输电线路的设计冰厚已完全考虑该路段除气象条件外的其他个性化要素,使线路相对覆冰灾害而言具有了均一化属性。在此基础上,参考已有研究[23],选取输电线路失效率模型作为易损性模型。线路的失效率函数[23]如式(4)所示。
| $ {\lambda _F}\left( x \right) = \left\{ \begin{array}{l} 0, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;x \le D\\ \exp \left[{\frac{{0.6931\left( {x-D} \right)}}{{4D}}} \right] -1, D < x < 5D\\ 1, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;, x \ge 5D \end{array} \right. $ | (4) |
式(4)中,x为覆冰厚度,D为线路设计覆冰厚度。在D < x < 5D时,失效率依指增长。
式(4)所示模型中,失效率与线路故障前的运行时间无关。该模型基于输电线路的物理受力分析,根据金属形变理论,当杆塔或线路应变较小时,承受能力随着应变的增大而增大;当承受能力达到承受极限后,随着应变的增加,承受能力呈指数迅速减小。在承受能力达到极限后,线路的失效率与承受能力成反比,线路的失效率呈指数函数上升[23]。
2.3 电网覆冰灾害风险评估根据区域灾害系统理论,灾害系统结构体系主要包括孕灾环境、致灾因子、承灾体,风险评估主要包括致灾因子危险性、承灾体易损性、孕灾环境稳定性和减灾能力等的综合评估[24]。其中,在电网覆冰灾害中,孕灾环境稳定性的影响通过DEM、风速、温度、压力等地理气象要素,间接作用于致灾因子的形成发展和承灾体的布设中。故在不考虑人为抗冰、消冰等减灾作用的情况下,覆冰灾害风险评估可简单表达为式(5)。
| $ R = H \times E $ | (5) |
其中,R表示风险,指覆冰灾害导致的电网失效率大小;H表示致灾因子,指不同概率(重现期)下覆冰强度;E表示承灾体,指不同分类、分布下承灾体在各种致灾因子强度下的损失概率。
3 浙江省示例 3.1 致灾因子危险性评估 3.1.1 历史覆冰过程重建本文利用浙江省气象科学研究所前期研发的覆冰生成数值模式,对2005—2014年冬季浙江省覆冰过程进行模拟。覆冰生成数值模式包括覆冰阶段判别和覆冰重量变化量模拟2个模块。模型以当前时次的气象要素(包括气温、相对湿度、降水量、风速、温湿度垂直廓线)和前一时次的覆冰重量和覆冰导线直径(初始时次的覆冰重量为0,覆冰导线直径等于导线直径)为输入数据,计算当前时次的标准冰厚。其基本流程如下:1)根据当前时次的气象要素,判别当前时次为维持阶段、雨凇覆冰增长阶段、雾凇覆冰增长阶段、热力融冰阶段或升华脱冰阶段;2)如果当前时次为积冰维持阶段,则当前时次的覆冰重量变化量为0;否则,用订正的Jones简单模型[25-27]、Makkonen模型[28, 29]、热力融冰或升华脱冰的经验公式[30],计算雨凇覆冰增长、雾凇覆冰增长、热力融冰或或升华脱冰引起的覆冰重量变化量;3)当前时次的积冰重量变化量与前一时次的积冰重量相加,得到当前时次的电线积冰重量,然后参照文献[31]推荐的方法,利用积冰重量计算出当前时次的标准冰厚。
模拟时间分辨率为1 h,空间分辨率为0.01°×0.01°。因数值模拟量较大,故结合前期研究结果和历史灾情资料[32],对2005—2011年冬季的覆冰灾害时段进行了初步筛选,具体模拟时段如表 1所示;对2011—2014年冬季进行时段全覆盖模拟。
|
|
表 1 覆冰生成模式模拟的2005—2011年覆冰灾害起止时段表 Table 1 Simulation periods for ice accretion model from 2005 to 2011 |
首先,基于以上覆冰灾害模拟结果,对各年年最大覆冰厚度进行抽样。然后,根据式(2),计算得到Gumbel函数参数。之后,以5、10、20、50 a一遇为例,根据式(3),计算典型重现期下浙江省最大覆冰厚度,绘制浙江省最大可能冰厚分布图,即冰区图(图 1)。从中可见,冰区分布主要呈现以下特征:1)就位置而言,浙江省沿海不易覆冰,内陆自北向南大致存在3条覆冰带,且冰带位置受山脉分布影响大。北部冰带大致沿里岗山—龙门山—会稽山—四明山一线山脊分布;中部自仙霞岭向东延伸,至大盘山、括苍山分为2支;南部大致沿洞宫山脉分布。2)就强度而言,中部冰带分布较为狭窄而覆冰强度大,北部、南部冰带覆盖范围较宽但覆冰极值较中部低。3)各重现期下冰区整体分布形势大致相同,进一步结合计算过程可知,随着年遇水平提高,覆冰强度和分布均现非线性增长。
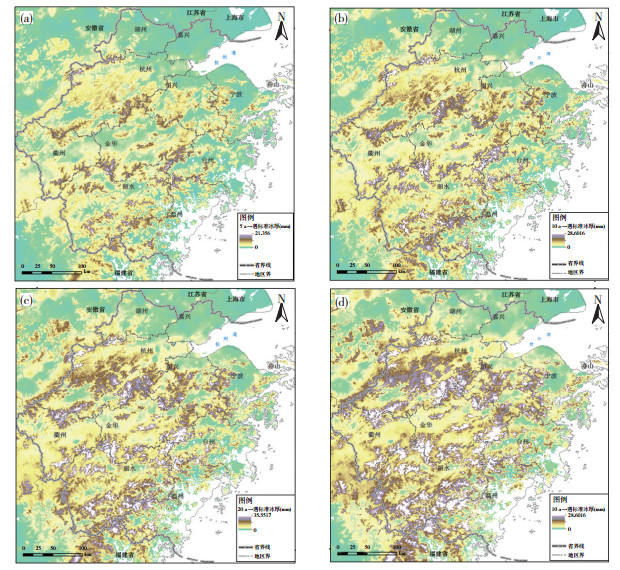
|
图 1 典型重现期(a. 5 a; b.10 a; c. 20 a; d. 50 a)下浙江省最大可能冰厚分布 Fig. 1 The distribution of possible maximum icing thickness in Zhejiang province under typical return periods of (a) 5 years, (b) 10 years, (c) 20 years, and (d) 50 years |
由于覆冰生成数值模式的计算单元为空间栅格,而实测覆冰厚度数据和灾情数据均针对具体杆塔,因此,需建立由栅格尺度向杆塔尺度覆冰厚度转化的降尺度方案。本节以2008年、2013年2场灾害电网故障段勘察数据为基础进行统计分析。
(1) 栅格模拟冰厚与杆塔实测冰厚的比较分析。图 2给出浙江省2008和2013年冰灾倒塔杆塔实测与其栅格模拟的最大覆冰厚度关系比较。从中可见,模拟值多小于实测值小。因模拟值是基于0.01°×0.01°空间单元均一地形、气象条件模拟的单位栅格平均覆冰厚度的过程最大值;而实测值是倒塔点单点单元的覆冰厚度,是覆冰厚度的过程最大值的空间极值点。分析认为,两者差异主要是因其反应的空间尺度不同。
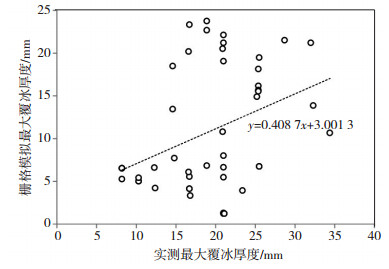
|
图 2 冰灾倒塔杆塔实测与其栅格模拟的最大覆冰厚度关系 Fig. 2 Relationship between measured and simulated maximum icing thickness of towers falling down |
杆塔冰厚的影响因素可分为两方面:一是孕灾环境,包括大气条件和下垫面条件,这类因素导致单位栅格内覆冰厚度不均;二是具体承灾体(即杆塔)的自身属性。从尺度上来看,0.01°×0.01° (约1 km)分辨率下局地气象条件(如气温、气压、风速、风向)差别不大,而下垫面的海拔、粗糙度、地形起伏等因素,以及杆塔自身属性对杆塔覆冰的局地差异性影响更大。
为定量考察各要素对杆塔冰厚的影响程度,进一步基于2场案例覆冰的实测和模拟数据,计算了覆冰厚度与环境变量、杆塔的各类属性变量的相关系数(表 2)。从中可见,故障段实测平均海拔与杆塔实测最大冰厚相关系数可达0.45,栅格平均DEM与栅格模拟最大冰厚相关系数可达0.67,均通过0.05水平的显著性检验。另外,杆塔实测最大冰厚与土地利用类型、气候背景以及导线是否耐张、同心度属性、电压等级、直径等属性相关性不大;栅格模拟最大冰厚与以上要素的相关性略有不同。可以看出,一是海拔及相关变量,与实测及模拟冰厚均有显著正相关关系,是影响覆冰厚度的重要因素;二是实测海拔与模型所用海拔数据对模拟冰厚有影响(表 2灰色阴影显示)。
|
|
表 2 实测及模拟冰厚与各影响因素之间的相关系数 Table 2 The correlation coefficient between measured/simulated ice thickness and the influencing factors |
进一步对实测海拔和模型中所用海拔数据进行对比,图 3给出浙江省2008和2013年冰灾倒塔杆塔实测海拔高度与覆冰生成模型中所用的海拔数据关系比较。从中可见,尽管两套数据的相关性很高(R= 0.737 0),但杆塔实测海拔整体高于杆塔所在栅格的平均海拔。结合表 2与图 2分析结果可以推测,覆冰过程局地极大值点很可能出现在海拔极大值点;模型所用栅格平均海拔数据与杆塔实测海拔的差异,是引起栅格冰厚与杆塔实测冰厚差异的主要原因。
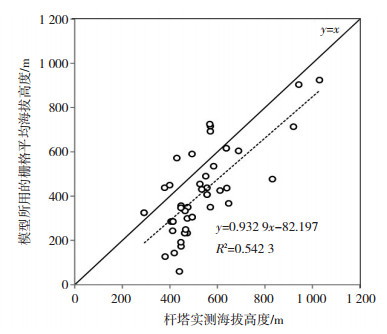
|
图 3 冰灾倒塔杆塔实测海拔高度与覆冰生成模型中所用的海拔数据关系 Fig. 3 Relationship between the measured altitude of towers falling down and the DEM data used in the ice accretion model |
(2) 杆塔覆冰估计方案。基于以上分析,本文通过引入模型所用的栅格平均海拔(Dm)与杆塔实测海拔(Do)之差这一物理量,将栅格模拟冰厚转化为杆塔模拟冰厚。统计覆冰厚度模拟值与实测值之差(Im-Io,以下简称模拟冰厚误差)、倒塔杆塔海拔之差(Dm-Do,以下简称海拔误差)的关系,图 4给出浙江省2008和2013年冰灾倒塔杆塔模拟冰厚误差与海拔误差的关系。从中可见,两序列相关系为0.38,通过0.01水平的显著性检验。因此,基于栅格覆冰模拟结果的杆塔覆冰估计方案设计如式(6)所示。
| $ y' = y-0.022\;5{\rm{ }}({D_m}-{D_o}) + 5.819\;5 $ | (6) |
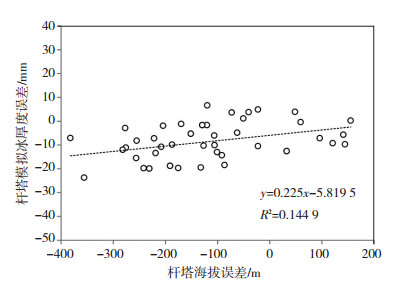
|
图 4 冰灾倒塔杆塔模拟冰厚误差与海拔误差的关系 Fig. 4 Relationship between ice thickness error and altitude error of towers falling down |
式(6)中,y′为校正后杆塔覆冰厚度,单位为mm;y为模拟的0.01°×0.01°栅格平均覆冰厚度,单位为mm;Do为杆塔实际海拔;Dm为0.01°×0.01°栅格平均海拔。
3.2 承灾体易损性评估本文2.3节易损性模型的适用关键在于设计覆冰厚度常数变量的获取。经文献考证[32],2009年后浙江省输电线路的设计覆冰厚度大都参照《浙江省输电线路设计标准分区》(2009),该分区综合考虑了风速和覆冰2种要素。此前输电线路线因架设年份较为久远而设计标准较难考证,假设设计分区延续性较好而差异不大。
根据设计标准分区,浙江省可以分为沿海无冰区、近海平原及丘陵区、近海山地区、西北部内陆地区共5类区域,其设计冰厚分别为0 mm、5 mm、10 mm、5 mm。考虑式(4)形式,当设计冰厚D为0而实际覆冰厚度x为非0时,失效率均为1;而实际并非设计冰厚为0区完全不能承受低强度覆冰。为使式(4)在沿海无冰区更具有适用性,本文将沿海无冰区的设计冰厚改为非零的较小正值,例如取0.2。
3.3 电网覆冰灾害风险评估基于2.4节所述理论方法,根据图 1结果,结合式(4)—(6),计算得到针对研究区杆塔尺度的、典型重现期下覆冰灾害的输电线路失效率(图 5)。从中可见,浙江中部及偏北部是输电线路覆冰灾害风险最为严重的区域;南部山区虽覆冰危险性不低(图 1),但由于输电线路设计覆冰估计较为充分,因此未来风险相对较低。
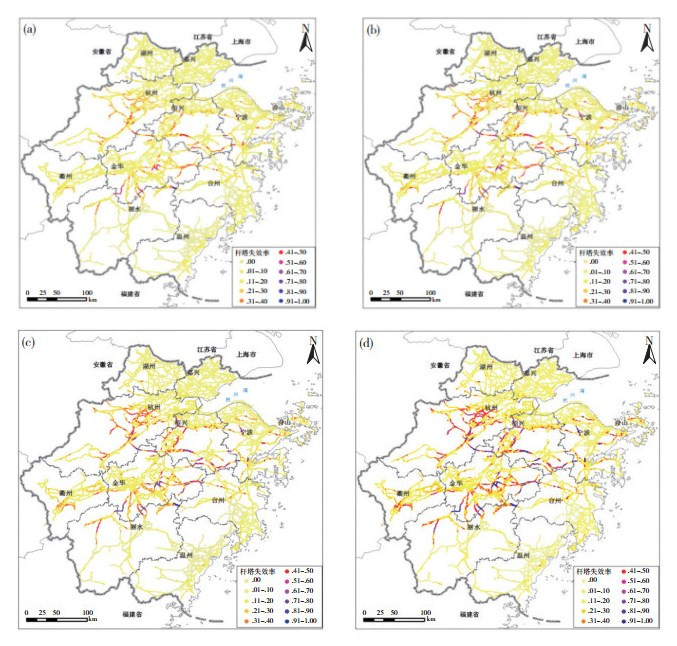
|
图 5 典型重现期(a. 5 a; b. 10 a; c. 20 a; d. 50 a)下输电线路杆塔覆冰失效率 Fig. 5 The distribution of failure rate of the towers along transmission line in Zhejiang province under typhical return period of (a) 5 years, (b) 10 years, (c) 20 years, and (d) 50 years |
本文以区域灾害系统理论为指导,探索基于超越概率方法的输电线路灾害风险评价思路,以浙江省为例对该方法进行释用,并绘制典型重现期下浙江省冰区图及电网失效图。主要结论如下:
(1) 基于常规气象站和自动气象站观测数据,通过覆冰生成数值模式反演历史覆冰过程,可一定程度上有效解决历史样本匮乏问题。以浙江省为例,逐小时0.01°×0.01°分辨率的历史覆冰过程反演可基本满足冰区图绘制需求。经验证,覆冰灾害过程清晰,灾害极值数据量值可信;结果显示,浙江省冰区分布呈北、中、南带状分布,且中部覆冰带可能强度最大。
(2) 通过环境要素、杆塔属性等与局地覆冰的关系探讨,进行栅格模拟覆冰向杆塔覆冰的降尺度研究。结果表明,海拔及相关变量,与实测及模拟冰厚均有显著正相关关系,是影响覆冰厚度的重要因素,海拔差异是引起单元栅格尺度范围内覆冰差异的主要原因。
(3) 基于自然灾害风险评估方法,选取易损性评估模型,对浙江省输电线路覆冰灾害下的电网失效率给出了定量评估。结果显示,在当前气候背景条件下,忽略人为抗冰、融冰等作用,浙江省中部及北部的输电线路将面临较大的覆冰风险,应采取积极的风险管理防灾减灾措施。
针对风险评估中历史样本长度问题有待进一步研究。笔者曾以台风灾害风险评估为例,就历史样本长度对风险评估中不同重现期影响展开专题讨论[33],认为历史样本长度越长,概率分布型越稳定、风险评估结果越可靠,重现期5 a以上的可靠风险评估,往往需要30 a以上样本。但就输电线路覆冰灾害而言,涉及浙江省境内的灾害历史记录匮乏,历史记录较长的常规站也难以客观真实反映覆冰灾害,一方面因数据时空分辨率太低而难以捕捉覆冰现象,另一方面因早期常规站往往布设海拔较低,对丘陵山区气候特点不具代表性。因此,本文研究时段选取了有自动站观测以来的最长年限为研究时段,重在探讨以超越概率方法进行输电线路覆冰灾害风险评估可行性。下一步将通过补充历史实测、利用中尺度模式重建天气、完善概率分布估计的极值理论方法等途径,进一步解决历史样本不足的问题。就研究结果而言,因样本有限,需注意致灾危险性估计和电网失效率结果在量值上的系统偏差,但其空间分布形势仍具有较好的参考价值。
| [1] |
胡毅, 刘凯, 吴田, 等. 输电线路运行安全影响因素分析及防治措施[J]. 高压电技术, 2014, 40(11): 3491-3499. |
| [2] |
李灿, 张礼平, 吴义城, 等. 南方极端雨雪冰冻过程东亚冬季风环流特征及与El Nino/La Nina事件的关系[J]. 暴雨灾害, 2010, 29(2): 142-147. DOI:10.3969/j.issn.1004-9045.2010.02.007 |
| [3] |
陈孝明, 胡淼, 黄俊杰. 湖北省电线积冰日数气候特征与大气环境异常的关系研究[J]. 暴雨灾害, 2015, 34(3): 260-267. DOI:10.3969/j.issn.1004-9045.2015.03.009 |
| [4] |
赵珊珊, 高歌, 张强, 等. 中国冰冻天气的气候特征[J]. 气象, 2010, 36(3): 34-38. |
| [5] |
温克刚. 中国气象灾害大典(综合卷)[M]. 北京: 气象出版社, 2008.
|
| [6] |
陈海涛, 谢承隆, 赵智敏. 冰雪自然灾害对浙江电网安全供电的影响和对策[J]. 上海电力, 2008, 21(5): 437-440. |
| [7] |
黄崇福. 综合风险评估的一个基本模式[J]. 应用基础与工程科学学报, 2008, 16(3): 371-381. DOI:10.3969/j.issn.1005-0930.2008.03.008 |
| [8] |
张勇军, 许亮, 吴成文. 计及多因素的电网冰灾风险评估模型研究[J]. 电力系统保护与控制, 2012, 40(15): 12-17. DOI:10.7667/j.issn.1674-3415.2012.15.003 |
| [9] |
潘斌, 张勇军, 黄慧. 多因子电网冰灾风险评估建模[J]. 电网技术, 2012, 36(5): 102-106. DOI:10.3969/j.issn.1674-0629.2012.05.024 |
| [10] |
孙羽, 王秀丽, 王建学, 等. 架空线路覆冰闪络跳闸特性分析与风险建模[J]. 中国电机工程学报, 2011, 31(31): 149-158. |
| [11] |
史培军. 三论灾害研究的理论与实践[J]. 自然灾害学报, 2002, 11(3): 1-9. DOI:10.3969/j.issn.1004-4574.2002.03.001 |
| [12] |
黄崇福. 自然灾害风险评价:理论与实践[M]. 北京: 科学出版社, 2005.
|
| [13] |
Kathleen F, Neal L, Ronald T. Extreme ice thicknesses from freezing rain[R]. New Hampshire, 2004
|
| [14] |
NEI Electric Power Engineering. New hampshire December 2008 ice storm[R]. Arvada, Colombia, 2008
|
| [15] |
龚强, 汪宏宇, 蔺娜, 等. 辽宁省电线积冰特征与电网冰区划分研究[J]. 冰川冻土, 2010, 32(3): 549-556. |
| [16] |
段旭, 段玮, 陶云, 等. 云南冰冻灾害研究与电线覆冰区划[M]. 北京, 2010.
|
| [17] |
吴素良, 范建勋, 宋丽莉, 等. 陕西省冰区划分[J]. 电网技术, 2010, 34(4): 152-157. |
| [18] |
杨加伦, 朱宽军, 刘彬, 等. 输电线路冰区分布图绘制关键技术[J]. 电力建设, 2013, 34(9): 31-36. DOI:10.3969/j.issn.1000-7229.2013.09.007 |
| [19] |
朱宽军.重点区域覆冰特性研究及冰区图的建立[R].中国电力科学研究院, 2009
|
| [20] |
丁裕国, 江志红. 极端气候研究方法导论[M]. 北京: 气象出版社, 2009.
|
| [21] |
龙立宏, 胡毅, 李景禄, 等. 输电线路冰害事故统计分析及防治措施研究[J]. 电力设备, 2006, 7(12): 26-28. |
| [22] |
黄俊杰, 周悦. 湖北省地形因子对电线覆冰的影响研究[J]. 暴雨灾害, 2015, 34(3): 254-259. DOI:10.3969/j.issn.1004-9045.2015.03.008 |
| [23] |
梅生伟, 薛安成, 张雪敏. 电力系统自组织临界特性与大电网安全[M]. 北京: 清华大学出版社, 2009.
|
| [24] |
史培军. 四论灾害系统研究的理论与实践[J]. 自然灾害学报, 2005, 14(6): 1-7. DOI:10.3969/j.issn.1004-4574.2005.06.001 |
| [25] |
Jones K F. A simple model for freezing rain ice loads[J]. Atmospheric research, 1998, 46(1): 87-97. |
| [26] |
Musilek P, Arnold D, Lozowski E P. An ice accretion forecasting system (IAFS) for power transmission lines using numerical weather prediction[J]. Scientific Online Letters on the Atmosphere, 2009, 5(1): 25-28. |
| [27] |
Pytlak P, Musilek P, Lozowski E, et al. Evolutionary optimization of an ice accretion forecasting system[J]. Monthly Weather Review, 2010, 138(7): 2913-2929. DOI:10.1175/2010MWR3130.1 |
| [28] |
Makkonen L. Modeling of ice accretion on wires[J]. Journal of Climate and Applied Meteorology, 1984, 23(6): 929-939. DOI:10.1175/1520-0450(1984)023<0929:MOIAOW>2.0.CO;2 |
| [29] |
Makkonen L, Lozowski E P. Numerical modelling of icing on power network equipment[M]. Berlin: Springer Netherlands, 2008.
|
| [30] |
Farzaneh M, Savadjiev K. Statistical analysis of field data for precipitation icing accretion on overhead power lines[J]. IEEE Transactions on Power Delivery, 2005, 20(2): 1080-1087. |
| [31] |
电力规划设计总院. 电力工程气象勘测技术规程(DL/T5158-2012)[M]. 北京: 中国电力出版社, 2012: 23-24.
|
| [32] |
浙江省电力公司, 浙江省电力设计院, 浙江省气象科学研究所.浙江省电网冰区分布图绘制技术报告[R].2013
|
| [33] |
李颖, 方伟华. 热带气旋降水重现期估算研究[J]. 自然灾害学报, 2014, 23(6): 58-69. |
 2017, Vol. 36
2017, Vol. 36 