2. 辽宁广播电视大学,沈阳 110034
2. Liaoning Radio and TV University, Shenyang 110034
受全球气候变化的影响,各地极端暴雨事件频繁发生,特别是最近二十多年城市化飞速发展的进程中,区域暴雨的时空分布和变化特征均可能发生了显著变化,暴雨强度(以下简称雨强)有所加强[1-4]。暴雨的变化趋势对城市的防灾减灾提出新的挑战,设计暴雨主要包括雨强和雨型两方面[5]。暴雨强度公式是科学合理制定城市和重大工程区域给排水工程规划和工程设计的重要基础[6-8],雨型主要用于确定设计暴雨的时间变化过程,可以更加准确的反映地表径流的产生过程和径流流量[9-10],雨型在排水管道系统计算模型建立时是必须的,在研究雨水调蓄系统时,也需采用雨型进行设计校核[11-13]。
葫芦岛市(锦西)现行的暴雨强度公式依据1962— 1982年的降雨资料所编制,观测资料有限且时间较早,已不能恰当反映当前的暴雨特征规律,也不能充分适应当前排水工程规划的需要,因此亟需编制新的暴雨强度公式。暴雨观测资料的累积及暴雨强度公式推算方法的深入研究,为新一代暴雨强度公式的推算提供了基础[14-16]。当前,常用的短历时暴雨雨型确定方法有芝加哥雨型、Huff法、Pilgrim和Cordery法等[5, 9]。芝加哥雨型法是当前相关导则中推荐采用的设计方法,已在国内外得到较广泛的应用[9, 17]。
本文依据《室外排水设计规范》[17]及《城市暴雨强度公式和设计暴雨雨型确定技术导则》[11],分别采用年最大值法和年多个样法,拟合多种概率模型,以确定最佳的新暴雨强度公式,并与现行(旧)暴雨强度公式进行对比分析。在此基础上,采用芝加哥雨型法确定短历时暴雨雨型,以期为城市排水设计等提供一定的参考。
1 资料与方法 1.1 资料葫芦岛城区仅有1个国家气象站(连山区气象站)具有长期降雨观测资料,本文选用该站作为代表站。所用资料为连山区气象站1959—2014年日降雨数据、1973—2014年分钟降雨数据。其中,1973—2003年分钟降雨数据为中国气象局统一开展的降雨自记纸信息化处理数据,该资料通过对降雨自记纸进行扫描、图像处理和数据处理,将降雨自记纸图像进行数字化转换,获得逐分钟降雨资料;2004—2014年分钟降雨数据为逐分钟的自动观测数据。根据滑动平均法计算1973—2014年5、l0、15、20、30、45、60、90、120、150、180 min共11个降雨历时的资料[11]。
1.2 方法 1.2.1 暴雨强度公式计算(1) 暴雨选样。年最大值法选样选取降雨资料样本中各降雨历时雨量的逐年最大值,即42个样本。
年多个样法选样则不论年次将各个降雨历时有效资料样本(每个历时有42×8个)按从大到小排序排列,并从大到小选取年数的4倍(42×4个)数据,作为统计样本。
(2) 频率分布曲线拟合。文献[11、17]推荐皮尔逊Ⅲ型(简称P-Ⅲ型)分布曲线、耿贝尔分布曲线和指数分布曲线,本文从中选取拟合效果较好、误差最小的概率分布函数曲线,推求暴雨强度公式。上述三种理论概论曲线的数学表达式以及原理等可参见文献[11]。
(3) 暴雨强度公式及参数求解。暴雨强度公式定义为[17]:
| $ q = \frac{{167{A_1}\left( {1 + C\lg P} \right)}}{{{{\left( {t + b} \right)}^n}}} $ | (1) |
式(1)中,q为雨强(单位:升/秒/公顷,L·s-1·hm-2),p为重现期(单位:a),t为降雨历时(单位:min)。A1、b、C、n是待求的相关参数:A1雨力参数(单位:mm),b为降雨历时修正参数,C为雨力变动参数,n为衰减指数。
对式(1)两边取对数得:
| $ \ln q = \ln 167{A_1} + \ln \left( {1 + C\lg P} \right) - n\ln \left( {t + b} \right) $ | (2) |
令y = ln q - ln(1 + ClgP),b0 = ln 167A1,b1 = -n,x = ln(t + b),即得:
| $ y = {b_0} + {b_1}x $ | (3) |
通过最小二乘法求参数,得到b0、b1值。
给定不同的b值,计算出相应的A1、n以及q′ (拟合值),并求出公式的平均绝对均方差σ:
| $ \bar \sigma = \frac{1}{{{m_0}}}\sum\limits_{j = 1}^{{m_0}} {\sqrt {\frac{1}{m}\sum\limits_{i = 1}^m {{{\left( {{q_{ij}} - {{q'}_{ij}}} \right)}^2}} } } $ | (4) |
式(4)中,m为11个历时,m0为8个重现期。
通过不断调整b值,使σ值达到最小。选取使σ最小的一组参数A1、b、n,即为最佳拟合值。
按《室外排水设计规范》[17]的要求,需计算抽样误差和暴雨公式均方差。重现期在2~20 a时,在一般降雨强度的地方,平均绝对均方差不超过0.05 mm·min-1;在较大降雨强度的地方,平均相对均方差不超过5 %。
平均绝对均方差为:
| $ {X_m} = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {{{\left( {\frac{{{{R'}_i} - {R_i}}}{{{t_i}}}} \right)}^2}} } $ | (5) |
平均相对均方差为:
| $ {U_m} = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {{{\left( {\frac{{{{R'}_i} - {R_i}}}{{{R_i}}}} \right)}^2}} } \times 100\% $ | (6) |
式(5)、(6)中,R′为理论降雨量,R为拟合曲线确定的降雨量,t为降雨历时,n为样本数。
1.2.2 芝加哥雨型设计方法(1) 雨峰位置系数确定。芝加哥雨型以暴雨强度公式为基础设计典型降雨过程。将各降雨历时的逐年降雨过程样本,以5 min为间隔进行分段,统计降雨过程的雨峰位置系数。
| $ r={}^{t}\!\!\diagup\!\!{}_{T}\; $ | (7) |
式(7)中,r为雨峰位置系数,t为雨峰值时刻,T为降雨历时。
将历时相同的入选降雨样本的雨峰位置系数进行算术平均,再将各历时的雨峰位置系数按照历时长度进行加权平均,计算出综合雨峰位置系数。
(2) 芝加哥降雨模型。雨峰前、后瞬时降雨强度可由以下两个公式计算:
| $ i\left( {{t_{{b}}}} \right) = \frac{{A\left[ {\frac{{\left( {1 - n} \right){t_b}}}{r} + b} \right]}}{{{{\left[ {\left( {\frac{{{t_{{b}}}}}{r}} \right) + b} \right]}^{n + 1}}}} $ | (8) |
| $ i\left( {{t_a}} \right) = \frac{{A\left[ {\frac{{\left( {1 - n} \right){t_a}}}{r} + b} \right]}}{{{{\left[ {\left( {\frac{{{t_{{a}}}}}{{1 - r}}} \right) + b} \right]}^{n + 1}}}} $ | (9) |
式(8)和(9)中,i(tb)、i(ta)分别为雨峰前、后的瞬时降雨强度(单位: mm·min-1),tb、ta为雨峰前、后相应的降雨历时(单位: min),b为降雨历时修正参数,n为衰减指数,r为雨峰位置系数。A = 167A1(1 + ClgP),其中A1为雨力参数(单位:mm),C为雨力变动参数,P为重现期(单位:a)。
根据雨峰位置系数和公式(8)、(9)计算合成暴雨过程的各时段(以5 min计)的平均降雨量和累计降雨量,再通过计算各时段的降雨强度确定对应短历时暴雨的芝加哥雨型。
2 新暴雨强度公式编制 2.1 估算方法的优选根据葫芦岛连山区气象站1973—2014年5、l0、15、20、30、45、60、90、120、150、180 min共11个历时降雨数据,采用年最大值法和年多个样法选样,依据三种频率分布曲线拟合,应用最小二乘法求参数,并计算均方差。辽宁地区属于一般降雨强度的地方,因此首要考虑平均绝对均方差,再参考平均相对均方差。
表 1给出多种暴雨强度公式推算结果精度检验,从中可见,采用年最大值法时,P-Ⅲ型分布曲线和耿贝尔分布曲线拟合公式的平均绝对均方差和相对均方差均满足规范要求;采用年多个样法时,仅P-Ⅲ型分布曲线拟合的暴雨强度公式平均绝对均方差满足规范要求。其中,年最大值法P-Ⅲ型分布曲线拟合的公式误差最小。
|
|
表 1 多种暴雨强度公式推算结果精度检验 Table 1 The accuracy test of storm intensity formula derived by different methods |
根据估算方法优选结果,采用年最大值法P-Ⅲ型分布曲线拟合的新暴雨强度公式精度最高,公式为:
| $ q = \frac{{756.649 \times \left( {1 + 0.984\lg P} \right)}}{{{{\left( {t + 5.483} \right)}^{0.528}}}} $ | (10) |
采用年多个样法P-Ⅲ型分布曲线拟合的新暴雨强度公式的绝对均方差也能满足要求,为:
| $ q = \frac{{658.773 \times \left( {1 + 0.737\lg P} \right)}}{{{{\left( {t + 1.950} \right)}^{0.469}}}} $ | (11) |
原有旧暴雨强度公式为:
| $ q = \frac{{1\;878 \times \left( {1 + 0.8\lg P} \right)}}{{{{\left( {t + 6} \right)}^{0.732}}}} $ | (12) |
式(10)、(11)和(12)中,q为雨强(单位: L·s-1 ·hm-2),p为重现期(单位:a),t为降雨历时(单位:min)。
3 新旧暴雨强度公式差异及原因分析 3.1 暴雨强度公式对比分析年最大值法新编暴雨强度公式与旧暴雨强度公式的差异,二者差值比率定义如下:
| $ {\varepsilon _1} = \frac{{{i_m} - {i_o}}}{{{i_o}}} \times 100\% $ | (13) |
式(13)中,im、io分别为年最大值法新编暴雨强度公式、旧暴雨强度公式计算的雨强(单位: L·s-1 ·hm-2)。分析年多个样法新编暴雨强度公式与旧暴雨强度公式间的差异,二者雨强差值比率定义如下:
| $ {\varepsilon _2} = \frac{{{i_n} - {i_o}}}{{{i_o}}} \times 100\% $ | (14) |
式(14)中,in、io分别为年多个样法新编暴雨强度公式、旧暴雨强度公式计算的雨强(单位: L·s-1·hm-2)。分析年最大值法与年多个样法新编暴雨强度公式的差异,二者雨强差值比率定义如下:
| $ {\varepsilon _3} = \frac{{{i_m} - {i_n}}}{{{i_m}}} \times 100\% $ | (15) |
式(15)中,im、in分别为年最大值法新编暴雨强度公式、年多个样法新编暴雨强度公式计算的雨强(单位: L·s-1 ·hm-2)。
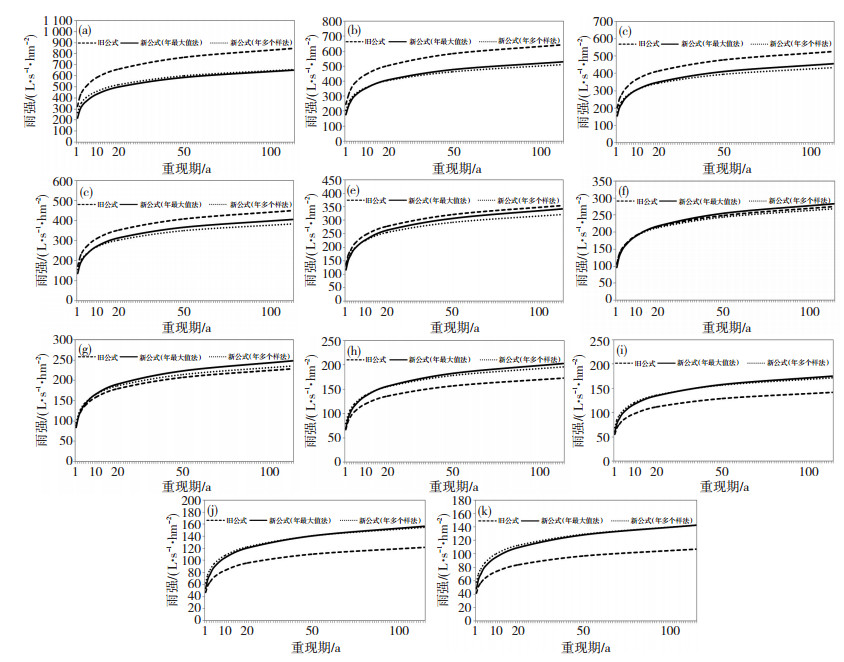
表 2给出年最大值法、年多个样法新编的暴雨强度公式和旧暴雨强度公式计算出的雨强差值比率,图 1给出各降雨历时雨强。从中可见,采用年最大值法和年多个样法推求的两个新编暴雨强度公式求得的雨强差异较小,后者推求的暴雨强度公式计算得到的5 min历时雨强均略大于前者推求的暴雨强度公式计算结果,其余各历时1~5 a重现期也均以后者推求的暴雨强度公式计算的雨强较大,之后随重现期增大,前者推求的暴雨强度公式计算的雨强逐渐偏大。
|
|
表 2 年最大值法、年多个样法新编暴雨强度公式和旧暴雨强度公式的雨强差值比率 Table 2 Difference ratios of rainstorm intensity calculated by the new formula of maximum method, annual multisampling method and the old formula |
|
图 1 年最大值法、年多个样法新编暴雨强度公式和旧暴雨强度公式各降雨历时雨强对比 (a) 5 min, (b) 10 min, (c) 15 min, (d) 20 min, (e) 30 min, (f) 45 min, (g) 60 min, (h) 90 min, (i) 120 min, (j) 150 min, (k) 180 min Fig. 1 Comparison of rainstorm intensity of different rainfall durations calculated by the new formula of maximum method, annual multisampling method and the old formula (a) 5 min, (b) 10 min, (c) 15 min, (d) 20 min, (e) 30 min, (f) 45 min, (g) 60 min, (h) 90 min, (i) 120 min, (j) 150 min, (k) 180 min |
两个新编暴雨强度公式求得的雨强均与旧暴雨强度公式有较大差异。5~30 min历时各重现期基本均以旧暴雨强度公式求得的雨强较大,45 min历时各公式各重现期雨强基本相当,60~180 min历时各重现期基本以新编暴雨强度公式求得的雨强较大。
考虑年最大值法和年多个样法推求的两个新编暴雨强度公式计算的各历时各重现期的雨强均较为接近,但文献[11]推荐采用年最大值法,且年最大值法拟合的精度也最高,因此本文推荐使用年最大值法P-Ⅲ型分布曲线拟合的新暴雨强度公式。
3.2 原因分析葫芦岛市新、旧暴雨强度公式采用的资料时段、采样方式、编制方法均有所不同,致使新、旧公式计算结果存在明显差异。现行(旧)暴雨强度公式由锦州市规划处利用1962—1982年的降雨资料,采用年多个样法取样,由数理统计方法推算得出,编制时间较早、资料序列较短、方法较为单一。新暴雨强度公式是利用1973—2014年逐分钟降雨资料,依据国家现行规范和导则推荐的方法得出,所用资料最新、资料序列长度满足规范要求、经过严格质量检验,且编制方法多样、规范。由于旧暴雨强度公式编制年代久远,且没有文献详细记载其计算方法和资料采样方式,因此,主要从降雨的气候变化特征对新、旧暴雨强度公式差异的原因进行分析。辽宁省气象信息中心仅有葫芦岛连山区气象站1959—2014年逐日降雨数据及1973— 2014年分钟降雨数据,因此根据1959—2014年日最大降雨量及1973—2014年各降雨历时最大降雨量进一步分析降雨变化特征。
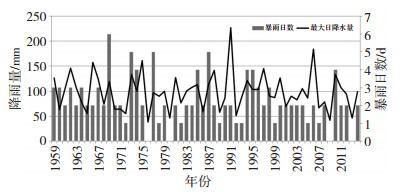
3.2.1 年日最大降雨量变化特征图 2给出葫芦岛市连山区气象站1959—2014年的年最大日降雨量及暴雨日数(日降雨量大于50 mm)的变化情况。从中可见,1962—1982年,日最大降雨量为161.3 mm (1975年),年暴雨日数最多为6 d (1969年),年日最大降雨量平均值为95.7 mm,年暴雨日数平均值为2.4 d;1983—2014年,日最大降雨量为227.3 mm (1991年),次大值为184.5 mm (2006年),年暴雨日数最多为5 d (1987年),年日最大降雨量平均值为100.2 mm,年暴雨日数平均值为2.1 d。总体来看,20世纪80年代以来降雨特征有较明显的变化,暴雨日数较80年代之前略有减少,但日最大降雨量却有显著增大趋势,即暴雨出现概率虽有所减小,但暴雨强度有增强趋势。
|
图 2 葫芦岛1959—2014年的年最大日降雨量及暴雨日数 Fig. 2 The annual maximum daily precipitation amount and rainstorm days at Huludao from 1959 to 2014 |
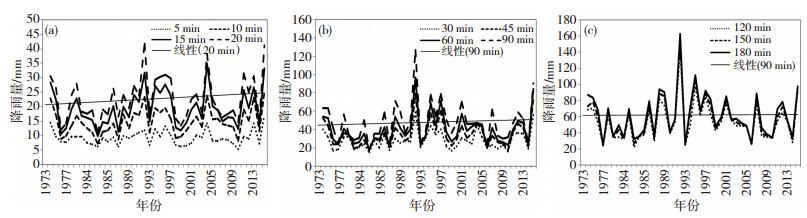
图 3给出葫芦岛市连山区气象站1973—2014年5、l0、15、20、30、45、60、90、120、150、180 min历时最大降雨量的变化。从中可见,随着降雨历时的增大,各历时最大降雨量的变化特征越来越接近,其中,5 min和10 min历时最大降雨量均出现在2014年,15 min历时最大降雨量出现在2003年,20~180 min历时最大降雨量均出现在1991年。表 3给出各历时最大降雨量的变化趋势系数和最大降雨量变率的气候倾向率。从中可见,各历时最大降雨量均有一定的增加趋势,气候倾向率在0.3~5.2 %·(10a-1),其中,10 min历时最大降雨量变率的气候倾向率最大,180 min的最小,但均未通过0.05的显著性检验。
|
图 3 葫芦岛1973—2014年各历时最大降雨量 Fig. 3 The maximum precipitation of different rainfall durations at Huludao from 1973 to 2014 |
|
|
表 3 葫芦岛1973—2014年各历时最大降雨量的趋势系数和最大降雨量变率(最大降雨量变化占最大降雨量平均值的比率)的气候倾向率(单位:%·(10a-1)) Table 3 The trend coefficient of maximum precipitation and climate tendency rate (unit: %·(10a-1)) of variety rate of maximum precipitation of different rainfall durations at Huludao from 1973 to 2014 |
总体来看,1973—2014年各历时最大降雨量均有明显的年际变化特征,且均有一定的增大趋势,各历时降雨量最大值均出现在1991年之后。选择1973— 2014年作为样本时段编制新暴雨强度公式是合理的,一方面保证样本为近期且长度大于30 a,另一方面尽量考虑保留最大值入选样本。旧暴雨强度公式利用的是1962—1982年数据,其涵盖的1973—1982年各历时最大降雨量普遍偏低,已不适用于当前暴雨特征规律。
4 短历时暴雨雨型暴雨雨型是指不同降雨历时内的雨强随时间的变化特征,而对市政或工程室外排水设计影响较大的为短历时暴雨雨型[5, 11]。依据文献[11]所推荐的芝加哥法,假定短历时暴雨雨型为单峰型。
4.1 暴雨雨峰位置系数芝加哥法暴雨雨型的确定需计算雨峰位置系数。首先,为能够获得不同降雨历时的降雨场次,以降雨时长选取,按照降雨历时±15 min确定(例如60 min降雨时长按照降雨历时45~75 min确定),以120 min作为最小降雨间隔,划分降雨场次,取每年降雨量最大的8个场次,将各降雨场次按照降雨量从大到小进行排序,根据确定的雨量阀值选取各历时降雨量大于雨量阀值的降雨场次进行综合分析。为验证计算结果的合理性,确定两种雨量阀值指标(a、b)进行对比分析。
表 4给出不同降雨历时的时长参考区间、雨量阀值指标及对应的雨峰位置系数。根据降雨阀值指标a,确定60、90、120、150、180 min降雨历时分别挑选出26、23、14、17、19场降雨,计算出雨峰位置系数分别为0.330、0.297、0.294、0.319、0.331,再按各降雨历时的长度对各历时的雨峰位置系数进行加权平均,求出综合雨峰位置系数为0.315。根据降雨阀值指标b,确定60、90、120、150、180 min降雨历时分别挑选出17、19、11、14、16场降雨,计算出雨峰位置系数分别为0.279、0.295、0.314、0.352、0.333,加权平均求出综合雨峰位置系数为0.323。总体来看,选取的降雨量阀值指标较小时,60~120 min的雨峰位置系数较大;选取的降雨量阀值指标较大时,150~180 min的雨峰位置系数较大;综合雨峰位置系数非常接近,均为0.32左右,因此,确定该地区综合雨峰位置系数为0.32。
|
|
表 4 不同降雨历时的时长参考区间、雨量阀值指标及对应的雨峰位置系数 Table 4 The reference continuous interval, threshold index of rainfall and rain peak position coefficient of different rainfall durations |
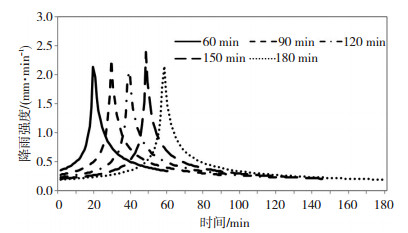
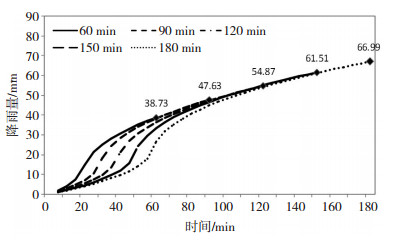
根据综合雨峰系数、暴雨重现期、降雨历时,代入雨峰前后瞬时降雨强度公式,计算出雨峰前后瞬时降雨强度及各个时段内的平均降雨强度,最终确定得到一定重现期及降雨历时的芝加哥暴雨雨型。当前我国中小城市排水管道的设计重现期为0.5~1 a一遇,设计标准较低,不能满足城市发展的现状,今后新建排水管道的设计重现期将逐步调整至2 a一遇以上。图 4给出芝加哥法推求重现期2 a的各降雨历时暴雨雨型分布,从中可见,重现期2 a历时60、90、120、150、180 min的降雨强度峰值在2.048~2.391 mm·min-1,差异较小,没有显著规律,雨峰出现时间分别为第19、29、39、48、58 min。图 5给出芝加哥法推求重现期2 a的各降雨历时累计降雨量,从中可见,重现期2 a历时60、90、120、150、180 min的累计降雨量在38.73~66.99 mm,各历时降雨均在初期累计降雨增长较慢,雨峰前后增长速度较快,之后增速明显放缓。
|
图 4 芝加哥法推求重现期2 a的各降雨历时暴雨雨型分布 Fig. 4 The distribution of designed rainstorm patterns of Chicago method of different rainfall durations of 2 a return period |
|
图 5 芝加哥法推求重现期2 a的各降雨历时累计降雨量 Fig. 5 Accumulated precipitation of Chicago method of different rainfall durations of 2 a return period |
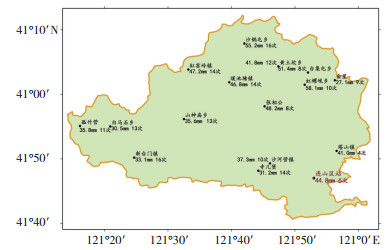
图 6给出葫芦岛市地形特征及气象站位置,从中可见,葫芦岛市地势西北高东南低,海拔在30—900 m,地形差异较大。连山区气象站位于葫芦岛市东南部沿海地区,距离葫芦岛市主城区较近,地形特征与葫芦岛市主城区接近,地形较为平缓。由于区域自动气象站观测年限较短且只获得逐时降雨资料,根据自动气象站降雨资料有效率情况,选取葫芦岛市14个区域自动站和国家气象站同期(2012年)逐时降雨资料,分析葫芦岛市小时最大降雨量和小时暴雨次数分布特征(图 7)。可见,葫芦岛市2012年小时最大降雨量在27.1~58.1 mm,小时暴雨次数在4~16次,小时最大降雨量最大值出现在东北部,小时暴雨次数最大值出现在西南部和北部。总体来说,葫芦岛市暴雨空间分布特征差异较大且具有较强的随机性。

|
图 6 葫芦岛市地形特征及气象站位置 Fig. 6 Terrain feature and location of meteorological stations at Huludao |
|
图 7 葫芦岛市小时最大降雨量(单位: mm)和小时暴雨次数分布特征 Fig. 7 Distribution characteristics of maximum hourly precipitation (unit: mm) and the number of hourly rainstorm at Huludao |
根据葫芦岛地形及暴雨分布特征,连山区气象站观测资料只能代表葫芦岛西南沿海主城区。因此,本文结论适用于葫芦岛主城区,周边地区仅可参考使用。
6 结论和讨论(1) 根据年最大值法和年多个样法,采用P-Ⅲ型分布曲线拟合得到的暴雨强度公式精度均能满足导则要求,推求的暴雨强度公式计算的雨强差异较小。根据估算方法优选结果,采用年最大值法P-Ⅲ型分布曲线拟合的新暴雨强度公式精度最高,因此推荐葫芦岛市暴雨强度公式选用式(10)。
(2) 新暴雨强度公式5~30 min历时各重现期雨强较旧暴雨强度公式偏小,45 min历时各公式各重现期的雨强基本相当,60~180 min历时各重现期雨强较旧暴雨强度公式偏大。
(3) 近年来,葫芦岛市暴雨出现概率虽有所减小,但暴雨强度有增强趋势,各历时最大降雨量均有一定的增大趋势。暴雨变化特征显著,导致新、旧暴雨强度公式的计算结果差异较大,新暴雨强度公式适用于当前暴雨特征。
(4) 基于芝加哥雨型法得到相应的短历时暴雨雨型,葫芦岛市短历时暴雨雨峰位置系数为0.32,以重现期2 a为例,历时60、90、120、150、180 min的峰值降雨强度在2.048~2.391 mm·min-1,雨峰出现时间分别为第19、29、39、48、58 min,累计降雨量在38.73~66.99 mm,各历时降雨均在初期累计降雨增长较慢,峰前后增长速度较快,之后增速明显放缓。
由于短历时暴雨局地性较强,空间差异明显,新暴雨强度公式和短历时暴雨雨型设计结果只适用于葫芦岛市主城区,其余区域仅可参考使用。本文仅采用了同期1 a的数据对比分析了葫芦岛市暴雨分布特征,今后将获取更多完整区域站数据进一步分析。
| [1] |
丁一汇, 任国玉, 石广玉, 等. 气候变化国家评估报告(1):中国气候变化的历史和未来趋势[J]. 气候变化研究进展, 2006, 2(1): 3-8. DOI:10.3969/j.issn.1673-1719.2006.01.001 |
| [2] |
翟盘茂, 李蕾. IPCC第五次评估报告反映的大气和地表观测变化[J]. 气候变化研究进展, 2014, 10(1): 20-24. DOI:10.3969/j.issn.1673-1719.2014.01.004 |
| [3] |
谢五三, 王胜. 近40 a淮河流域暴雨特征分析[J]. 暴雨灾害, 2010, 12(4): 377-380. DOI:10.3969/j.issn.1004-9045.2010.04.013 |
| [4] |
吴滨, 文明章, 李玲, 等. 福建省不同短历时暴雨时空分布特征[J]. 暴雨灾害, 2015, 6(2): 153-159. DOI:10.3969/j.issn.1004-9045.2015.02.007 |
| [5] |
岑国平, 沈晋, 范荣生. 城市设计暴雨雨型研究[J]. 水科学进展, 1998, 9(1): 41-46. DOI:10.3321/j.issn:1001-6791.1998.01.007 |
| [6] |
王敏, 谭向诚. 北京城市暴雨和雨型的研究[J]. 水文, 1994(3): 1-6. |
| [7] |
张秉祥, 陈静, 韩军彩, 等. 石家庄市城区暴雨强度公式修正方法对比分析[J]. 干旱气象, 2014, 32(4): 671-676. |
| [8] |
陈正洪, 王海军, 张小丽. 深圳市新一代暴雨强度公式的研制[J]. 自然灾害学报, 2007, 16(3): 29-34. DOI:10.3969/j.issn.1004-4574.2007.03.006 |
| [9] |
庄智福, 王珂清, 杨杰, 等. 镇江市新一代暴雨强度公式编制及雨型设计[J]. 气象科学, 2015, 35(4): 506-513. |
| [10] |
成丹, 陈正洪, 方怡. 宜昌市区短历时暴雨雨型特征[J]. 暴雨灾害, 2015, 34(3): 249-253. DOI:10.3969/j.issn.1004-9045.2015.03.007 |
| [11] |
住房和城乡建设部, 中国气象局. 城市暴雨强度公式编制和设计暴雨雨型确定技术导则[M]. 北京: 气象出版社, 2014: 1-25.
|
| [12] |
Amell V, Harremoes P, Jensen M, et al. Review of rainfall data application for design and analysis[J]. Water Sci. Technol, 1984, 16(8-9): 1-45. DOI:10.2166/wst.1984.0176 |
| [13] |
顾俊强, 徐集云, 陈海燕, 等. 暴雨强度公式参数估计及其应用[J]. 南京气象学院学报, 2000, 23(1): 63-67. DOI:10.3969/j.issn.1674-7097.2000.01.010 |
| [14] |
陈正洪, 王海军, 张小丽, 等. 水文学中雨强公式参数求解的一种最有方法[J]. 应用气象学报, 2007, 18(2): 237-241. DOI:10.3969/j.issn.1001-7313.2007.02.015 |
| [15] |
金家明. 城市暴雨强度公式编制及其应用方法[J]. 中国市政工程, 2010(1): 38-39, 41. DOI:10.3969/j.issn.1004-4655.2010.01.015 |
| [16] |
植石群, 宋丽莉, 罗金铃, 等. 暴雨强度计算系统及其应用[J]. 气象, 2000, 26(6): 30-33. DOI:10.3969/j.issn.1000-0526.2000.06.007 |
| [17] |
中华人民共和国住房和城乡建设部. 室外排水设计规范(GB50014-2006, 2014年版)[M]. 北京: 中国计划出版社, 2014.
|
 2017, Vol. 36
2017, Vol. 36 