2. 河海大学水文水资源学院,南京 210098;
3. 中国气象局公共气象服务中心,北京 100081;
4. 四川省青川县气象局,青川 628100
2. College of hydrology and Water Recourses, Hohai University, Nanjing 210098;
3. Public Meteorological Service Centre, CMA, Beijing 100081;
4. Qingchuan Meteorological Station of Sichuan Province, Qingchuan 628100
山洪是指山区溪沟小流域突发性暴涨暴落的地表径流[1-3]。它由短历时来水(强降水、融雪、冰川融水等)诱发,常发生在山丘小区域内,往往造成社会经济和人民群众生命财产严重损失。近几十年来,气候变暖背景下极端天气事件发生频率有所升高,山丘区小流域因面积小、坡陡、汇流时间短,在突发性暴雨条件下极易引发山洪灾害,这已成为国内外学者的研究热点[3-8]。目前,国外常用的山洪预报预警方法主要有两种:基于分布式水文模型的山洪过程预报[9]和基于临界雨量阈值的山洪预警评估[10]。2006年10月27日国务院正式批复的《全国山洪灾害防治规划报告》指出,山洪流域为面积为200 km2以内的山区型小流域,其流域往往因为没有水文站而称为无资料山洪流域。无资料流域水文过程涉及水文科学的基础理论和方法,一直是水文学研究的难点,这也给山洪预报预警带来更大技术困难[11]。
由IAHS (International Association of Hydrological Sciences)开展的PUB (Predictions in Ungaged Basins) 10 a (2003-2013年)国际合作计划项目是在水文理论和多源资料应用方面探寻解决无资料流域水文预报难题的重要项目[12-13]。分布式水文模型更好地考虑了降水和下垫面条件的空间变异性,使之能更好地利用GIS技术、遥感与遥测等空间信息描述水文过程的机理与模拟流域的降雨-径流响应在PUB项目进展过程中发挥重要的推动作用[14-19, 25]。应用水文模型进行无资料流域山洪预报的关键难点是没有长序列水文数据进行模型参数率定。Foody等[20]尝试应用基于经验SCS曲线和马斯京根法的半分布式水文模型进行无资料流域山洪预报,其模型参数直接由地形和植被覆盖数据获取。Vieux等[21]指出,基于Green-Ampt下渗理论的分布式水文模型可很好地描述山洪定量化过程。Chahinian等[22]在山洪预报中比较应用了Horton、Philip和SCS等产流模型。Estupinaborrell等[1]指出,山洪径流形成过程产流机制包含蓄满产流与超渗产流,且在径流形成过程中常常同时存在。在预报中只考虑单一产流机制往往导致预报结果出现一定的偏差[23]。
本研究引入在新安江水文模型基础之上建立的分布式混合产流水文模型[24] (Grid-and-Mixed-run off-generation-and-Kinematic-wave-based Hydrological Model,GMKHM),研究无资料小流域山洪预报方法。模型结合DEM、RS技术,以DEM栅格为计算单元,栅格内进行植被冠层截留、蒸散(发)、产流与分水源计算;用混合产流模型计算流域产流,考虑栅格间水量交换和水系排水影响[25],坡面汇流和河道汇流均采用逐栅格的分布式运动波模型水流演算,模型参数基于DEM、GIS和RS技术先验估计直接获取。然后,将GMKHM模型和分布式新安江水文模型[16, 26]应用于嘉陵江乔庄河支流大沟小流域进行汛期(2009年)山洪预报试验,探讨分布式水文模型的山洪模拟预报性能。
1 资料与GMKHM水文模型 1.1 资料来源本次研究中使用的1″× 1″分辨率的DEM (Digital Elevation Model)数据是由美国国家航空航天局(NASA)和国防部国家测绘局(NIMA)提供,30″× 30″分辨率的植被覆盖数据是由美国马里兰大学(University of Maryland)提供,30″× 30″分辨率的土壤类型数据是由联合国粮农组织(FAO)和维也纳国际应用系统研究所(IIASA)所构建的世界土壤数据库(HWSD)提供。
1.2 GMKHM水文模型GMKHM模型是以流域内的DEM栅格作为水文响应过程的基本单元,并假设单元栅格内地形地貌、陆面植被覆盖和土壤组成类型等下垫面条件和降水强迫空间分布一致,GMKHM模型中只考虑DEM栅格间水文要素的变异性。在栅格水文单元中,由植被冠层截留和蒸散(发)计算后得到的净雨量,再经混合产流计算与水源划分后,根据河网逐栅格汇流演算次序,依次将地表径流、壤中流与地下径流演算至流域出口断面,得到其水文过程[24]。在单元栅格垂直方向上分为植被层、上层土壤、下层土壤、深层土壤四层。在植被层考虑植被截留,对三层土壤层采用新安江水文模型[27]的三层蒸散(发)模型进行蒸散(发)计算,应用考虑蓄满与超渗两种产流机制的混合产流模型进行栅格内产流计算;坡面汇流和河道汇流均采用逐栅格的一维运动波水流演算模型。在逐栅格分布式汇流模型中,采用文献[28]提出的方法处理上游栅格入流:将其作为当前栅格单元产流计算中的降水量的一部分处理,当此栅格为河道栅格,径流量将按比例汇入河道。
1.2.1 陆面植被冠层截留陆面植被冠层截留主要是通过植被冠层表面吸着力、承托力及水分重力、表面张力等作用截留的降水量[29]。植被冠层对降水的累积截留公式可表示为[30]
| $ {I_{{\rm{cum}}}} = {f_{\rm{lc}}}{S_{{\rm{c}}\;{\rm{max}}}}(1-{e^{-{C_{{\rm{vd}}}}{P_{{\rm{cum}}}}{\rm{/}}{S_{{\rm{c}}\;{\rm{max}}}}}}) $ | (1) |
式(1)中,Icum为植被冠层的累积截留量(单位: mm);fk为植被覆盖率,可由叶面指数与作物高度求得[31-33];Pcum为累积降雨量(单位: mm);Cvd为植被密度的校正因子;Scmax为植被冠层的截留能力(单位: mm),即植被冠层的最大截留量。Cvd和Scmax均可由叶面指数求得。根据植被冠层的累积截留量即可获得每个计算时段的冠层截留量,即
| $ {I_{{\rm{ca}}}}(t) = {I_{{\rm{cum}}}}(t)-{I_{{\rm{cum}}}}(t-{\rm{ }}Dt) $ | (2) |
式(2)中,Ica(t)为t时刻的植被冠层截留量;Δt为模型计算的时间步长。
1.2.2 混合产流模型新安江模型的核心内容与特色技术是由河海大学赵人俊教授[24, 27]提出的蓄满产流模型。该模型是在GMKHM模型中,模型产流在蓄满产流机制的基础之上考虑了超渗产流机制,即认为栅格水文单元内的超渗产流只发生在不蓄满部分上。
单元栅格水文单元内用于产流计算的净雨(PE,单位: mm)可由式(3)计算得到。
| $ {P_{\rm{E}}} = P-ET + \frac{{1000 \cdot {Q_{{\rm{up}}}} \cdot \Delta t}}{{{A_{\rm{c}}}}} $ | (3) |
式(3)中,Qup为上游入流(单位: m3·s-1);Δt为模型计算的时间步长(单位: s);Ac为单元栅格面积(单位: m2)。
当PE>0时,当前单元栅格将产流;否则,不产流。当单元栅格产流时,由发生蓄满产流面积(FR)上的产流量(R)则可根据式(4)得到产流面积。
| $ {F_{\rm{R}}} = R/{P_{\rm{E}}} $ | (4) |
从而在不蓄满流域面积(1 - FR)上进行超渗产流计算。李致家等[34]提出,如果忽略土壤层水力传导度差异性分布,超渗产流仅有超渗坡面流。实际上,超渗坡面流在流域汇流时往往出现超渗坡面流、饱和坡面流、壤中流和地下径流交替出现的现象[24]。基于此,GMKHM模型假设在栅格单元不蓄满部分上有一定比例(λ)超渗产流与蓄满产流混合进入自由水蓄水库进行分水源,其余部分作为超渗坡面流直接汇入河网。GMKHM模型引入Bf次方的抛物线来考虑不蓄满面积上下渗能力的空间分布不均匀性[24]。即
| $ \delta = 1-{(1-\frac{f}{{{f_{{\rm{mm}}}}}})^{{B_{\rm{f}}}}} $ | (5) |
式(5)中,f为下渗能力;δ为下渗能力小于f的面积比例;fmm为栅格单元内的最大下渗能力。超渗产流irs的计算公式为
| $ irs = ({P_{\rm{E}}}-{f_{{\rm{mm}}}}) \times (1-{F_{\rm{R}}}) \times {f_{\rm{p}}}\;\;({P_{\rm{E}}} \ge {f_{{\rm{mm}}}}) $ | (6) |
| $ \begin{array}{l} irs = \left( {{P_{\rm{E}}}-\frac{{{f_{{\rm{mm}}}}}}{{{B_{\rm{f}}} + 1}}\left( {1-{\rm{ }}{{\left( {1-\frac{{{P_{\rm{E}}}}}{{{f_{{\rm{mm}}}}}}} \right)}^{{B_{\rm{f}}} + 1}}} \right)} \right) \times (1 - {F_{\rm{R}}}) \times {f_{\rm{p}}}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;({P_{\rm{E}}} < {f_{{\rm{mm}}}}) \end{array} $ | (7) |
式(6)、(7)中,fp为超渗产流发生的面积比例。超渗产流量(irs × λ)与蓄满产流量混合通过自由水蓄水库分水源计算调节出流[24]。
当
| $ {R_{\rm{S}}} = \{ {P_{\rm{E}}}- {S_{\rm{M}}} + S + {S_{\rm{M}}}{[1-({P_{\rm{E}}} + {A_{\rm{U}}})/{S_{{\rm{MM}}}}]^{1 + {E_{\rm{X}}}}}\} \times {F_{\rm{R}}} $ | (8) |
当
| $ {R_{\rm{S}}} = ({P_{\rm{E}}}-{S_{\rm{M}}} + S) \times {F_{\rm{R}}} $ | (9) |
自由水蓄水库的蓄水量由式(10)计算得到。
| $ S = S + {P_{\rm{E}}} + \frac{{irs}}{{{F_{\rm{R}}}}} \times \lambda-\frac{{{R_{\rm{S}}}}}{{{F_{\rm{R}}}}} $ | (10) |
其中,RS为产流量;S为自由水蓄水库的蓄水量。其余超渗产流量irs ×(1 - λ)作为超渗坡面流进行河网汇流。
综上可知,单元栅格的下渗能力f是混合产流模型计算的关键。在GMKHM模型中,采用Green - Ampt下渗方法计算f [35-36]。即
| $ f = \frac{{{\rm{d}}F}}{{{\rm{d}}t}} = {K_{\rm{S}}}\left[{\frac{{1 + ({\theta _{\rm{s}}}-{\theta _0}){S_{\rm{f}}}}}{F}} \right] $ | (11) |
| $ F = {K_{\rm{s}}} \cdot t-{S_{\rm{f}}}({\theta _{\rm{s}}}-{\theta _0}){\rm{ln}}\left( {1 + \frac{F}{{{S_{\rm{f}}}({\theta _{\rm{s}}}-{\theta _0})}}} \right) $ | (12) |
式(11)-(12)中,F为累积入渗量;Ks为有效水力传导度;t为时间;Sf为湿润峰面处土壤吸力;θs为饱和含水率;θ0为初始含水率。
1.2.3 一维运动波汇流模型GMKHM模型采用一维运动演算模型进行流域内逐栅格汇流计算。在坡面栅格中假设存在“虚拟河道”,径流通过“虚拟河道”进入进行河道水流一维运动波汇流。对于宽度为B、长度为L、净雨强为PE(x, t)的单元栅格坡面,可用运动波来描述[37]。即
| $ B\frac{\partial h}{\partial t}+\frac{\partial }{\partial x}\left( \frac{Bh}{n}{{R}^{{}^{2}\!\!\diagup\!\!{}_{3}\;}}\sqrt{{{S}_{0}}} \right)={{P}_{\text{E}}}(x,t) $ | (13) |
式(13)中,h为坡面径流深度(单位: m);R为水力半径;t为时间(单位: s);x为流径长度(单位: m);So为沿出流方向的地表坡度,在运动波方程中与地表摩阻比降相同。
由于坡面上的水流属于宽浅水流,可用水深h近似代替水力半径R,故上式可写成
| $ B\frac{{\partial h}}{{\partial t}} + \frac{{B\sqrt {{S_0}} }}{n}\frac{\partial }{{\partial x}}\left( {{h^{{}^{5}\!\!\diagup\!\!{}_{3}\;}}} \right) = {P_{\rm{E}}}(x, t) $ | (14) |
利用基于二分法的Preissmann隐式差分格式可对方程(14)进行离散化求解[37]。
河道水流运动的一维运动波方程组为
| $ \left\{ \begin{array}{l} \frac{{\partial {A_{{\rm{ch}}}}}}{{\partial t}} + \frac{{\partial {Q_{{\rm{ch}}}}}}{{\partial x}} = {q_1}\\ {S_{{\rm{oc}}}} = {S_{{\rm{fc}}}} \end{array} \right. $ | (15) |
式(15)中,Ach为河道断面的过水面积(单位: m2);Qch为河道流量(单位: m3·s-1);ql为单宽旁侧入流(单位: m3·s-1);Soc为河道坡度;Sfc为河道摩阻比降;hch为河道水深(单位: m)。河道水流运动波方程组的求解方法与坡面汇流方法相同。
1.2.4 模型参数先验估计依据GMKHM模型参数与流域地貌特征、土壤类型以及植被覆盖等之间的关系,对模型参数进行先验估计。模型有些参数可直接通过每个栅格单元的土壤类型和植被覆盖类型估计,如叶面指数(LAI)、最大叶面指数(LAImax)、作物高度(hlc)可由LADS直接获取[38],地表曼宁糙率系数(nh)可由陆面地表覆盖类型得到[39]。
产流模型(含分水源)参数包括蓄满产流与超渗产流两类参数。单元栅格张力水容量(WM)、自由水蓄水容量(SM)根据赵人俊教授[16, 40-41]在比较新安江模型与SACRAMENTO模型后得出WM与SM的计算公式为
| $ {W_{\rm{M}}} = ({\theta _{{\rm{fc}}}}-{\theta _{{\rm{wp}}}}) \times {L_{\rm{a}}} $ | (16) |
| $ {S_{\rm{M}}} = ({\theta _{\rm{s}}}-{\theta _{{\rm{fc}}}}) \times {L_{\rm{h}}} $ | (17) |
式(16)-(17)中,θs为饱和含水量;θfc为田间持水量;θwp为凋萎含水量;La为包气带厚度(单位: m);Lh为腐殖质土层厚度(单位: m)。θs、θfc、θwp均可根据栅格单元的土壤类型获取[42], La和Lh与单元栅格的地形指数与植被类型存在定量化关系[43]。
壤中流的出流系数(Ki)和地下水的出流系数(Kg)之和表示自由水出流的快慢,与土壤类型有关[44]。即
| $ {K_{\rm{i}}} + {K_{\rm{g}}} = 0.7 $ | (18) |
| $ \frac{{{K_{\rm{i}}}}}{{{K_{\rm{g}}}}} = \frac{{1 + 2(1-{\theta _{{\rm{wp}}}})}}{{{m_{\rm{r}}}}} $ | (19) |
式(19)中,mr为自由水出流校正系数,一般取值为1。
超渗产流计算中,Green-Ampt下渗方法中参数的有效水力传导度(Ks)、湿润锋面土壤吸力(Sf)均从相关水文学手册中取值[45];饱和含水率θs由栅格单元的土壤类型获取[42];稳定下渗率(fc),下渗能力分布曲线指数(Bf)、超渗产流面积比例(fp)分别根据文献[24]、文献[27]与文献[34]提供的经验数据取值。
蒸散(发)参数主要为上层土壤的张力水蓄水容量(WUM)、下层土壤的张力水蓄水容量(WLM)、深层蒸散发系数(C)和蒸散发折算系数(K)。WUM和WLM可由式(16)求得,C与栅格单元的植被覆盖率有关,在植被密集地区可取0.18,因此可假定其与植被覆盖率的比值为0.18[43]。K主要与测量水面蒸发所用的蒸发器有关,对于国内普遍采用的E-601蒸发皿而言,一般取值1。
汇流参数包括河道曼宁糙率系数(nc)、地表坡度(Soh)和河道坡度(Soc)。河道曼宁糙率系数(nc)可根据文献[43]推求。
| $ {n_{\rm{c}}} = {n_0}S_{{\rm{oc}}}^{{k_1}}A_{\rm{d}}^{{k_2}} $ | (20) |
式(20)中,k1与k2为经验系数;Ad为上游汇水面积(单位: km2);n0为流域出口栅格的曼宁糙率系数。k1、k2和n0为均可由经验关系获取[46-47]。
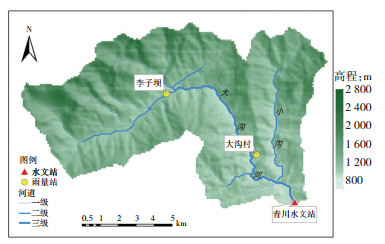
2 研究流域本研究选择嘉陵江乔庄河支流大沟流域青川水文站以上控制流域(图 1)作为小流域洪水预报验证流域。青川水文站以上控制的大沟流域面积为79.8 km2,占乔庄河流域总面积的10.6%。其中,四川境内面积占全流域面积的37.6%,涉及广元市青川县的乔庄镇;甘肃境内流域面积占大沟流域总面积的62.4%,涉及陇南市文县的碧口镇。流域内有两个雨量站(李子坝站和大沟村站)和一个水文站(青川水文站)。
|
图 1 嘉陵江乔庄河支流大沟流域地貌图 Fig. 1 Topographic map for Dagou basin of Qiaozhuanghe tributary of Jialingjiang River. |
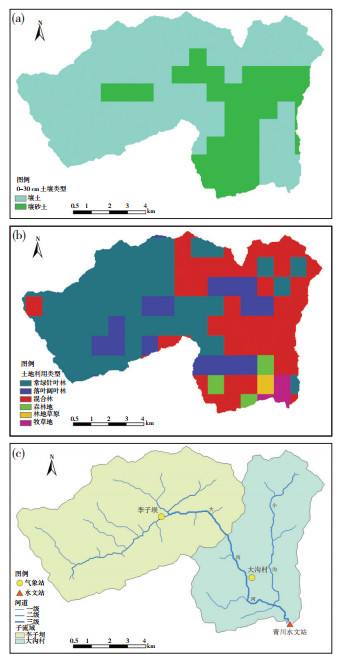
大沟流域位于秦巴山地,流域大部为山区或半山区,流域内海拔高度由北向南呈递减趋势。地势西北高、东南低,山脉纵横,谷深坡陡,地形起幅高程范围在800~1 850 m之间(图 1)。流域表层土壤类型主要为壤土和壤砂土。其中,壤土主要分布在西北部高山区以及乔庄镇所在的流域出口位置。其它地势较低的低山河谷区多为壤砂土(图 2a)。而下层土壤由西北向东南呈现粘壤土、砂壤土到壤土的过渡趋势。
|
图 2 嘉陵江乔庄河支流大沟流域0~30 cm土壤类型(a)、土地利用类型(b)以及水系与分块(c)分布图 Fig. 2 (a) 0-30 cm soil type map, (b) land cover map and (c) basin map and division parts for Dagou basin of Qiaozhuanghe tributary of Jialingjiang River. |
大沟流域内的土地利用类型主要是常绿针叶林和混合林,其中常绿针叶林主要分布在大沟流域西北高山区,而混合林主要分布在流域下游低山和河谷区(图 2b)。
该流域内自然生态条件优良,气候条件好,无污染,土壤酸碱性适度,无农药残留物,重金属含量低,森林覆盖率高,终年云雾缭绕,具有独特的自然生态优势。其年均降水量为1 027 mm。可能会发生的自然灾害包括旱灾、风灾、洪灾、雹灾等。大沟流域内沟谷发育,水网密布,大小溪沟河流甚多,其中流域内的干流为大沟河,支流为小沟,均是乔庄河的一部分,属嘉陵江水系(图 2c)。
3 基于分布式水文模型的大沟流域山洪预报考虑所能获取的水文资料有限,本研究运用GMKHM模型和分布式新安江水文模型[16-17, 26, 28, 48-50]对大沟流域2009年山洪过程预报试验和对比研究。
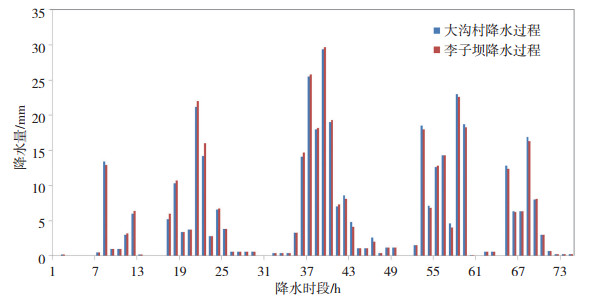
2009年7月14日16时至7月17日17时,大沟流域连续发生5次强降水过程(表 1和图 3,以降水间歇划分),流域累计降水量达到395.4 mm,流域单点最大雨强(29.7 mm·h-1)出现在7月16日06-07时的李子坝站。强降水导致该流域出现一次明显的多峰洪水陡涨陡落过程,其中第三次与第四次强降水导致的两个洪峰最大。
|
图 3 2009年7月14日16时-7月17日17时不同时段大沟流域大沟村站和李子坝站降水量变化(单位: mm)横坐标下“1”表示7月14日17时,“73”表示7月17日17时,余此类推 Fig. 3 Variation of rainfall (unit: mm) at Dagoucun station and Liziba station in the Dagou basin from 16:00 BT 14 to 17:00 BT 17 July 2009. The numbers of"1"and"73"below the abscissa indicate 17:00 BT 14 and 17:00 BT 17 July, respectively, and the rest may be inferred by analogy. |
|
|
表 1 2009年7月14日16时—7月17日17时大沟流域5次强降水过程概况 Table 1 Characteristics of 5 severe precipitation events occurred in the Dagou basin from 16:00 BT 14 to 17:00 BT 17 July 2009. |
应用分布式混合产流水文模型和分布式新安江水文模型对2009年大沟流域山洪过程进行模拟预报。考虑到大沟站与李子坝站降水过程量级相差不大,可近似认为本次降水过程流域内降水分布相对均匀,分布式水文模型输入的格点降水强迫采用图 3c中子流域划分方案,即:李子坝站所属的子流域内降水均用李子坝站的降水作为模型降水输入,大沟村站所属的子流域内降水均用大沟村站的降水作为模型输入。GMKHM模型中的fc、Bf、fp参数值,根据文献[24]、[27]和[34]分别取值为10.0 mm·h-1、0.07、0.85,其余参数均采用本文第1.2.4节的模型参数先验估计方法直接获取(图 4)。为了更好地与GMKHM模型进行对比验证,分布式新安江水文模型的汇流也采用一维运动波演算模型,且分布式新安江水文模型的植被冠层截留、蒸散发、蓄满产流、汇流参数均取与GMKHM模型的一致。

|
图 4 大沟流域单元栅格张力水容量WM(a,单位: mm)和自由水蓄水容量SM(b,单位: mm)的取值空间分布 Fig. 4 Value distribution based on grid-cell of (a) WM(unit: mm) and (b) SM(unit: mm) in the Dagou basin. |
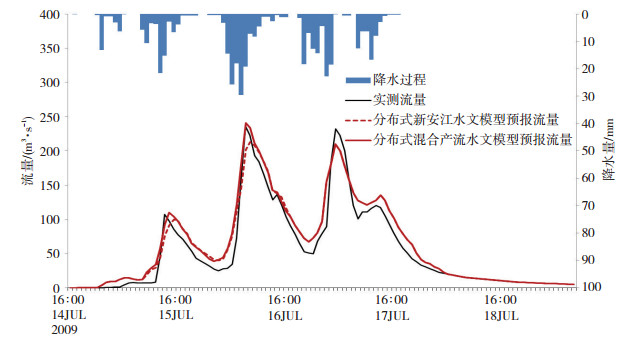
图 5为分布式混合产流水文模型与分布式新安江水文模型对2009年2月14日-19日大沟流域洪水过程的模拟预报图,表 2为两个模型在大沟流域应用模拟预报特征值表。从图 5和表 2中可见,两个水文模型都较好地模拟出本次洪水过程,两个分布式水文模型对本次洪水过程的模拟效果均较好: GMKHM模型和分布式新安江水文模型的径流深误差分别为16.6%和14.1%,洪峰误差分别为3.5%和-9.8%,洪峰出现时间误差分别为0 h和滞后1 h。根据《水文情报预报规范》 [51]中的相关指标,上述两个模型对本次洪水过程的预报均为合格。GMKHM模型模拟预报的确定性系数为0.94,达到甲等预报精度;分布式新安江水文模型模拟预报的确定性系数为0.89,也达到了乙等预报精度。总体而言,GMKHM模型在洪峰预报以及预报过程与实况洪水过程吻合度上的表现均比分布式新安江水文模型更好。
|
图 5 2009年7月14日16时-7月19日08时嘉陵江乔庄河支流大沟流域洪水模拟预报 Fig. 5 Simulation and forecast of the flood event occurred in Dagou basin of Qiaozhuanghe tributary of Jialingjiang River from 16:00 BT 14 to 08:00 BT 19 July 2009. |
|
|
表 2 两种分布式水文模型在大沟流域应用模拟预报特征值 Table 2 Simulation results of the flood event occurred in Dagou basin based on two types of distributed hydrological models. |
从前三次洪水上涨过程的模拟预报结果看,前两次GMKHM模型的预报过程要比分布式新安江水文模型涨幅要快,特别是峰值附近的预报,伴随着降水强度的突然增大,GMKHM模型明显高于分布式新安江水文模型的模拟结果,更接近实测值。这也说明在短历时强降水引发的山洪过程中,不仅包含蓄满产流,还有一定比例的超渗产流。相比仅考虑蓄满产流机制的分布式新安江水文模型,基于蓄满、超渗混合产流机制的GMKHM模型在洪峰预报上更具优势。对于第三个洪峰预报,两个分布式水文模型的表现几乎相同。其原因主要是前期降水过程的下渗量已经导致流域土壤含水量基本饱和,全流域反映单一产流机制,致使产生的径流过程也是基本相同。
4 结论与讨论无资料小流域的山洪预报一直是非常复杂的预报难题。本文选取流域面积仅为79.8 km2的嘉陵江乔庄河支流大沟小流域为研究对象,对该流域2009年汛期山洪过程进行了山洪预报试验。由于山洪径流形成过程产流机制包含蓄满产流与超渗产流,且这两类产流在径流形成过程中常常同时存在,所以,在对山洪的具体预报中若只考虑单一产流机制往往会导致预报结果出现一定的偏差。本文选用GMKHM模型和分布式新安江水文模型作为山洪预报模型进行大沟流域预报试验表明,两个分布式水文模型的模拟预报精度较高,均可用于对该流域山洪进行预报,其中GMKHM分布式水文模型在洪峰模拟预报和与实况洪水过程吻合程度上要好于分布式新安江水文模型。这也证明了山洪形成过程中存在一定比例的超渗产流,尤其对洪峰影响较大。对无资料小流域山洪预报有一定的借鉴意义。
本文使用的分布式水文模型参数均来自于模型的先验估计并直接应用。由于DEM、遥感信息(RS)等数据都存在一定的不确定性以及部分经验取值有误差,这使得获取的参数值不可避免存在一定偏差,所以,预报结果仍有再提高的必要和可能,特别是洪水的退水部分。另外,本文在小流域山洪预报试验中,由于能获取的水文资料有限,仅针对2009年汛期洪水过程进行了预报试验,虽然取得不错的预报结果,但还需要在更多山洪流域与山洪个例中验证预报模型的合理性与适用性。
| [1] |
Estupinaborrell V, Dartus D, Ababou R. Flash flood modeling with the MARINE hydrological distributed model[J]. Hydrol Earth Syst Sci Discuss, 2006, 3(6): 3397-3438. DOI:10.5194/hessd-3-3397-2006 |
| [2] |
国家防汛抗旱总指挥部办公室, 中国科学院水利部成都山地灾害与环境研究所. 山洪诱发的泥石流、滑坡灾害及防治[M]. 北京: 科学出版社, 1994.
|
| [3] |
叶金印, 吴勇拓, 李致家, 等. 湿润地区中小河流山洪预报方法研究与应用[J]. 河海大学学报:自然科学版, 2012, 40(6): 615-621. |
| [4] |
彭涛, 李俊, 殷志远, 等. 基于集合降水预报产品的汛期洪水预报试验[J]. 暴雨灾害, 2010, 29(3): 274-278. DOI:10.3969/j.issn.1004-9045.2010.03.012 |
| [5] |
刘志雨, 侯爱中, 王秀庆. 基于分布式水文模型的中小河流洪水预报技术[J]. 水文, 2015, 35(1): 1-6. |
| [6] |
Amengual A, Romero R, Gómez M, et al. A Hydrometeorological Modeling Study of a Flash-Flood Event over Catalonia, Spain[J]. Journal of Hydrometeorology, 2007, 8(3): 282. DOI:10.1175/JHM577.1 |
| [7] |
Borga M, Anagnostou E N, Blöschl G, et al. Flash flood forecasting, warning and risk management: the HYDRATE project[J]. Environmental Science & Policy, 2011, 14(7): 834-844. |
| [8] |
Alfieri L, Thielen J, Pappenberger F. Ensemble hydro-meteorological simulation for flash flood early detection in southern Switzerland[J]. Journal of Hydrology, 2012, s424-425(5): 143-153. |
| [9] |
水利部水文局(水利信息中心). 中小河流山洪监测与预警预测技术研究[M]. 北京: 科学出版社, 2010.
|
| [10] |
刘志雨, 杨大文, 胡健伟. 基于动态临界雨量的中小河流山洪预警方法及其应用[J]. 北京师范大学学报:自然科学版, 2010, 46(3): 317-321. |
| [11] |
姚成, 章玉霞, 李致家, 等. 无资料地区水文模拟及相似性分析[J]. 河海大学学报:自然科学版, 2013, 41(2): 108-113. |
| [12] |
Sivapalan M, Takeuchi K, Franks S W, et al. IAHS Decade on Predictions in Ungauged Basins (PUB), 2003-2012: Shaping an exciting future for the hydrological sciences[J]. Hydrological Sciences Journal / journal Des Sciences Hydrologiques, 2003, 48(6): 857-880. DOI:10.1623/hysj.48.6.857.51421 |
| [13] |
贾仰文, 王浩, 倪广恒. 分布式流域水文模型原理与实践[M]. 北京: 中国水利电出版社, 2005.
|
| [14] |
刘苏峡, 刘昌明, 赵卫民. 无测站流域水文预测(PUB)的研究方法[J]. 地理科学进展, 2010, 29(11): 1333-1339. DOI:10.11820/dlkxjz.2010.11.014 |
| [15] |
Bárdossy A, Singh S K. Robust estimation of hydrological model parameters[J]. Hydrology & Earth System Sciences, 2008, 12(6): 1273-1283. |
| [16] |
Yao C, Li Z J, Bao H J, et al. Application of a Developed Grid-Xinanjiang Model to Chinese Watersheds for Flood Forecasting Purpose[J]. Journal of Hydrologic Engineering, 2009, 14(9): 923-934. DOI:10.1061/(ASCE)HE.1943-5584.0000067 |
| [17] |
Yao C, Li Z, Yu Z, et al. A priori parameter estimates for a distributed, grid-based Xinanjiang model using geographically based information[J]. Journal of Hydrology, 2012, 468-469(6): 47-62. |
| [18] |
Li Z J, Zhang K. Comparison of Three GIS-Based Hydrological Models[J]. Journal of Hydrologic Engineering, 2008, 13(5): 364-370. DOI:10.1061/(ASCE)1084-0699(2008)13:5(364) |
| [19] |
Yao C, Zhang K, Yu Z, et al. Improving the flood prediction capability of the Xinanjiang model in ungauged nested catchments by coupling it with the geomorphologic instantaneous unit hydrograph[J]. Journal of Hydrology, 2014, 517(2): 1035-1048. |
| [20] |
Foody G M, Ghoneim E M, Arnell N W. Predicting locations sensitive to flash flooding in an arid environment[J]. Journal of Hydrology, 2004, 292(1-4): 48-58. DOI:10.1016/j.jhydrol.2003.12.045 |
| [21] |
Vieux B E, Cui Z, Gaur A. Evaluation of a physics-based distributed hydrologic model for flood forecasting[J]. Journal of Hydrology, 2004, 298(1-4): 155-177. DOI:10.1016/j.jhydrol.2004.03.035 |
| [22] |
Chahinian N, Moussa R, Andrieux P, et al. Comparison of infiltration models to simulate flood events at the field scale[J]. Journal of Hydrology, 2005, 306(1-4): 191-214. DOI:10.1016/j.jhydrol.2004.09.009 |
| [23] |
包为民, 赵丽平, 王金忠, 等. 垂向混合产流模型参数的线性化率定[J]. 水力发电学报, 2014, 33(4): 85-91. |
| [24] |
包红军, 王莉莉, 李致家, 等. 基于混合产流与二维运动波汇流分布式水文模型[J]. 水电能源科学, 2016, 34(11): 1-4, 21. |
| [25] |
包红军, 王莉莉, 李致家, 等. 基于Holtan产流的分布式水文模型[J]. 河海大学学报:自然科学版, 2016, 44(4): 340-346. |
| [26] |
Bao Hongjun. Coupling Ensemble weather predictions based on TIGGE database with Grid-Xinanjiang model for flood forecast[J]. Advances in Geosciences, 2011, 29: 61-67. DOI:10.5194/adgeo-29-61-2011 |
| [27] |
赵人俊. 流域水文模拟--新安江模型与陕北模型[J]. 北京:水利水电出版社, 1984. |
| [28] |
李致家, 姚成, 章玉霞, 等. 栅格型新安江模型的研究[J]. 水力发电学报, 2009, 28(2): 25-34. |
| [29] |
芮孝芳. 水文学原理[M]. 北京: 中国水利水电出版社, 2004.
|
| [30] |
Aston A R. Rainfall interception by eight small trees[J]. Journal of Hydrology, 1979, 42(3-4): 383-396. DOI:10.1016/0022-1694(79)90057-X |
| [31] |
Allan R G, Pereira L S, Raes D, et al. Crop evapotranspiration-Guidelines for computing crop water requirements-FAO Irrigation and drainage[G]. FAO, 1998: 56
|
| [32] |
Duchemin B, Hadria R, Er-Raki S, et al. Monitoring wheat phenology and irrigation in Central Morocco: on the use of relationship between evapotranspiration, crops coefficients, leaf area index and remotely-sensed vegetation indices[J]. Agric Water Manage, 2006, 79: 1-27. DOI:10.1016/j.agwat.2005.02.013 |
| [33] |
Er-Raki S, Chehbouni A, Guemouria N, et al. Combining FAO-56 model and ground-based remote sensing to estimate water consumptions of wheat crops in a semi-arid region[J]. Agricultural Water Management, 2007, 87(1): 41-54. DOI:10.1016/j.agwat.2006.02.004 |
| [34] |
李致家, 孔祥光. 对新安江模型的改进[J]. 水文, 1998(4): 19-23. |
| [35] |
王莉莉, 李致家, 包红军. 基于栅格的分布式超渗产流水文模型构建及比较[J]. 河海大学学报:自然科学版, 2010, 38(2): 123-128. |
| [36] |
Wang Lili, Li Zhijia, Bao Hongjun. Application of Developed Grid-GA Distributed Hydrologic Model in Semi-Humid and Semi-Arid Basin[J]. Transactions of Tianjin University, 2010, 16(3): 209-215. DOI:10.1007/s12209-010-0037-y |
| [37] |
王莉莉. 基于栅格的超渗产流水文模型研究及比较应用[D]. 南京: 河海大学, 2010
|
| [38] |
Land Data Assimilation Schemes (LDAS): Mapped Vegetation Parameters[EB/OL]. [2015-07-12]. http://ldas.gsfc.nasa.gov/LDAS8th/MAPPED.VEG/LDASmapveg.shtml
|
| [39] |
Vieux B E. Distributed hydrologic modeling using GIS[J]. Water Science & Technology Library, 2004, 38(3): 1-17. |
| [40] |
赵人俊. 萨克拉门托模型参数的分析[A]//刘光文, 姜弘道, 王厥谋, 等. 赵人俊水文预报文集[C]. 北京: 水利电力出版社, 1994: 199-208
|
| [41] |
李致家, 董增川, 梁忠民, 等. 大流域洪水预报与洪水调度管理方法研究[J]. 水力发电, 2004, 30(1): 12-15. |
| [42] |
Anderson R M, Koren V I, Reed S M. Using SSURGO data to improve Sacramento Model a priori parameter estimates[J]. Journal of Hydrology, 2006, 320(1-2): 103-116. DOI:10.1016/j.jhydrol.2005.07.020 |
| [43] |
姚成. Grid-Xinanjiang模型研究[D]. 南京: 河海大学, 2009
|
| [44] |
赵人俊, 王佩兰. 新安江模型参数的分析[J]. 水文, 1988(6): 4-11. |
| [45] |
Maidment D R. Handbook of Hydrology[M]. New York: Mcgraw-Hill Publ Comp, 1993
|
| [46] |
Tokar A S, Johnson P. Optimization of river characteristics in the Blue Nile watershed[R]. Technical Note 121, In: Koren V (Ed), NFS 3. 0 Reference Manual, US Department of Commerce, NOAA, Silver Spring, MD, 1995
|
| [47] |
Arcement G J, Schneider V R. Guide for selecting Manning's roughness coefficients for natural channels and flood plains[J]. Water-supply Paper of United States Geological Survey, 1989, 2339. |
| [48] |
包红军. 沂沭泗流域洪水预报调度模型应用研究[D]. 南京: 河海大学, 2006
|
| [49] |
李致家. 水文模型的应用与研究[M]. 南京: 河海大学出版社, 2008.
|
| [50] |
王莉莉, 李致家, 包红军. 基于DEM栅格的水文模型在沂河流域的应用[J]. 水利学报, 2007(s1): 422-427. |
| [51] |
中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会. 水文情报预报规范[S]. 北京: 中国标准出版社, 2008
|
 2017, Vol. 36
2017, Vol. 36 