2. 湖北大学材料科学与工程学院 武汉 430062;
3. 中国科学院电工研究所 北京 100190
2. College of Materials Science and Engineering of Hubei University, Wuhan 430062;
3. Institute of Electrical Engineering, Chinese Academy of Sciences, Beijing 100190
2014年11月,湖北省建设了新型三维闪电定位系统,该系统通过接收闪电回击辐射的VLF/LF脉冲信号,采用三维时差定位方法(3D Time of Arrival, 3D-TOA)又称为双曲线定位,实现了闪电VLF/LF辐射源的时间、位置、高度、强度及极性等主要参数的三维定位,系统既能探测云地闪又能探测云闪。目前,国内关于二维时差定位系统已做了大量研究,而对三维时差定位系统的研究相对较少。叶朝谋等[1]、俞志强等[2]、曾辉等[3]对三维时差定位系统的模糊及无解进行了相关分析,并提供了次优解的方法来解决无解现象。廖海军等[4]针对四站时差无源定位系统,分析了最优布站配置的影响因素及策略,并通过最小方差数据处理的改进算法提出了最优布站策略。张萍等[5]基于云闪的雷电定位系统分析了主要的误差来源,指出研究探测站位置关系及数量的重要性,通过优化布站策略及增加探测站数目,减小定位误差。田彩霞等[6]对江苏省的三维闪电定位实验网进行了matlab仿真,但只与雷达回波数据进行了定性的比较,缺乏实际的雷灾案例数据。禹继等[7]利用人工触发闪电试验及高建筑物自然闪电观测试验,对粤港澳闪电定位系统探测效率及精确度进行了评估,得到了闪电探测效率和回击探测效率,不涉及自然闪电的探测效率。而湖北地区建设的三维闪电定位系统的定位误差尚未开展相关的研究,本文通过布网结构研究,选择最优化的站网布局,主要讨论湖北地区VLF/LF三维闪电定位系统的误差,以期为更好地开展强对流天气的监测预报、雷电灾害监测预警、雷灾调查鉴定、雷击灾害风险评估与防御等现代气象业务奠定基础。
2 三维闪电定位的基本原理3D-TOA闪电定位算法是一种重要且较精确的闪电定位方式,通过处理4个或更多观测站接收到的信号到达时间数据,对闪电辐射源信号进行定位[8-9]。在二维平面中,闪电辐射源信号到达2个观测站的时间差确定了一对以2站为焦点的双曲线,利用3个站则可以确定2对双曲线来产生交点,即定位出了辐射源信号的经度及纬度信息。以此类推,若要确定立体空间中的任一闪电辐射源信号,除了需要定位经度及纬度参量以外,还需要定位高度信息,则至少需要4个站产生三对双曲面,面与面相交得线,线与面相交得点,以此来确定闪电辐射源信号的位置[5],在本研究中,定位的是空间辐射源信号最强点的位置信息。
2.1 定位模型图 1给出4站时差定位系统布站示意图。假定各观测站的空间坐标为(xi, yi, zi), i =0, 1, 2, 3, 其中i =0为主站,i =1, 2, 3为副站,闪电辐射源的坐标为(x, y, z),则闪电辐射源与各个站点存在如下关系式[6]:
| $ \left( {{t_i} - t} \right)c = \sqrt {{{\left( {x - {x_i}} \right)}^2} + {{\left( {y - {y_i}} \right)}^2} + {{\left( {z - {z_i}} \right)}^2}} $ | (1) |
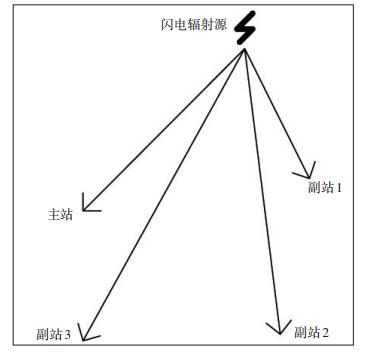
|
图 1 4站时差定位系统布站示意图 Fig. 1 Distribution for four-station TDOA location system. |
式(1)中,t为闪电发生的时间,ti为测得的信号到达时间,c为大气中的光速[1-3, 10]。
将式(1)展开、整理可得:
| $ {c^2}\left( {{t^2} + t_i^2 - 2{t_i}t} \right) = {R^2} + R_i^2 - 2{x_i}x - 2{y_i}y - 2{z_i}z $ | (2) |
其中
| $ \begin{array}{*{20}{c}} {\left( {{x_i} - {x_j}} \right)x + \left( {{y_i} - {y_j}} \right)y + \left( {{z_i} - {z_j}} \right)z - {c^2}\left( {{t_i} - {t_j}} \right)t = }\\ {\frac{{\left( {R_i^2 - R_j^2} \right) - c\left( {t_i^2 - t_j^2} \right)}}{2}} \end{array} $ | (3) |
式(3)中,i≠j,将其组成线性方程组,直接利用克拉默法则求解该线性方程组,可得闪电发生的位置。若方程组的系数行列式不等于零,则方程组有唯一解,若方程组的系数行列式等于零,则无解或有两个不同的解,此时参照文献[1]处理。
2.2 定位的误差分析设闪电定位误差为dx,dy,dz,且各探测站(xi, yi, zi)的站址误差及其误差分量dxi, dyi, dzi之间非相关,根据误差传递原理[4],对下式等号两边求微分:
| $ \begin{array}{*{20}{c}} {\left( {{t_i} - {t_0}} \right)c = \sqrt {{{\left( {x - {x_i}} \right)}^2} + {{\left( {y - {y_i}} \right)}^2} + {{\left( {z - {z_i}} \right)}^2}} - }\\ {\sqrt {{{\left( {x - {x_0}} \right)}^2} + {{\left( {y - {y_0}} \right)}^2} + {{\left( {z - {z_0}} \right)}^2}} } \end{array} $ | (4) |
为简化表达,令
| $ \begin{array}{*{20}{c}} {\Delta {R_i} = \left( {{t_i} - {t_0}} \right)c,{R_i} = \sqrt {{{\left( {x - {x_i}} \right)}^2} + {{\left( {y - {y_i}} \right)}^2} + {{\left( {z - {z_i}} \right)}^2}} ,}\\ {{R_0} = \sqrt {{{\left( {x - {x_0}} \right)}^2} + {{\left( {y - {y_0}} \right)}^2} + {{\left( {z - {z_0}} \right)}^2}} 。} \end{array} $ |
化简得:
| $ \begin{array}{*{20}{c}} {{\rm{d}}\left( {\Delta {R_i}} \right) = \left( {{c_{ix}} - {c_{0x}}} \right){\rm{d}}x + \left( {{c_{iy}} - {c_{0y}}} \right){\rm{d}}y + \left( {{c_{iz}} - {c_{0z}}} \right)}\\ {{\rm{d}}z + \left( {{k_0} - {k_i}} \right)\;\;\left( {i = 1,2,3} \right)} \end{array} $ | (5) |
式(5)中:
| $ {\rm{d}}\Delta R = C{\rm{d}}X + {\rm{d}}{X_s} $ | (6) |
式(6)中:
| $ {\rm{d}}\Delta R = \left[ {\begin{array}{*{20}{c}} {{\rm{d}}\left( {\Delta {R_1}} \right)}\\ {{\rm{d}}\left( {\Delta {R_2}} \right)}\\ {{\rm{d}}\left( {\Delta {R_3}} \right)} \end{array}} \right],{\rm{d}}X = \left[ {\begin{array}{*{20}{c}} {{\rm{d}}x}\\ {{\rm{d}}y}\\ {{\rm{d}}z} \end{array}} \right],{\rm{d}}{X_s} = \left[ {\begin{array}{*{20}{c}} {{k_0} - {k_1}}\\ {{k_0} - {k_2}}\\ {{k_0} - {k_3}} \end{array}} \right], $ |
| $ C = \left[ {\begin{array}{*{20}{c}} {{c_{1x}} - {c_{ox}}}&{{c_{1y}} - {c_{oy}}}&{{c_{1z}} - {c_{oz}}}\\ {{c_{2x}} - {c_{ox}}}&{{c_{2y}} - {c_{oy}}}&{{c_{2z}} - {c_{oz}}}\\ {{c_{3x}} - {c_{ox}}}&{{c_{3y}} - {c_{oy}}}&{{c_{3z}} - {c_{oz}}} \end{array}} \right] $ |
用伪逆法解式(6)得定位误差估计值为:
| $ {\rm{d}}X = {\left( {{C^T}C} \right)^{ - 1}}{C^T}\left[ {{\rm{d}}\Delta R - {\rm{d}}{X_s}} \right] $ | (7) |
令
式(7)中,dΔR为测量误差,表明目标定位与各观测站的到达时间有关;dXs表明目标定位与各观测站站址有关系;dX表明各时间差测量中均包含着时间传递误差、定时误差等共同误差因素。考虑到站址布局误差在各次测量时保持不变,且站址布局误差各元素之间及各站址误差之间互不关联,故闪电定位误差的协方差为[4]:
| $ {P_{dX}} = E\left[ {{\rm{d}}X{\rm{d}}{X^T}} \right] = B\left\{ {E\left[ {{\rm{d}}\Delta R{\rm{d}}\Delta {R^T}} \right] + E\left[ {{\rm{d}}{X_S}{\rm{d}}{X_S}^T} \right]} \right\}{B^T} $ | (8) |
若σx2、σy2、σz2分别表示为定位误差在x、y、z方向的方差,则定位精度GDOP可表示为:
| $ GDOP = \sqrt {\sigma _x^2 + \sigma _y^2 + \sigma _z^2} = {\left[ {\sum\limits_{i = 1}^3 {\sum\limits_{j = 1}^3 {\left( {{b_{1i}}{b_{1j}} + {b_{2i}}{b_{2j}} + {b_{3i}}{b_{3j}}} \right){\sigma _{ij}}} } } \right]^2} $ | (9) |
式(9)中,
由于上述算法是三维直角坐标系空间,而湖北省闪电定位网得到的信息是各站点的经度、纬度和高度,这就必须通过坐标转换后,才能利用上述算法。图 2给出在同一基准下,空间直角坐标系与空间大地坐标系的转换模型[11]。
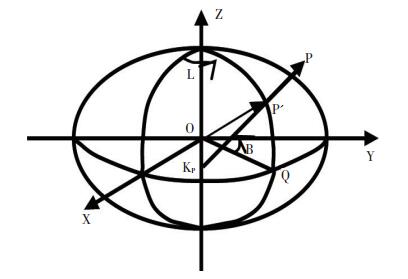
|
图 2 空间直角坐标系与大地坐标系转换模型图 Fig. 2 Transformation between 3D cartesian coordinate system and geodetic system. |
从图 2可知,空间直角坐标系的Z轴是地球自转轴,X轴位于赤道平面,指向格林尼治天文台,而Y轴指向东,构成右手系;空间大地坐标系中,B (纬度)为过一点的椭球面的法线与赤道面交角,L (经度)为过同一点的子午面与起始子午面二面角的平面角,H (高度)为点沿法线到椭球面的距离。把地球看作一个椭球,其方程及相关物理元素为:
| $ \frac{{{X^2}}}{{{a^2}}} + \frac{{{Y^2}}}{{{a^2}}} + \frac{{{Z^2}}}{{{b^2}}} = 1 $ | (10) |
椭球方程式(10)中,a为长半轴,b为短半轴,a = 6 378.17 km,b =6 356.75 km。
另有
| $ {r_{OP'}} = {\left( {\begin{array}{*{20}{c}} X\\ Y\\ Z \end{array}} \right)_{P'}} = \left( {\begin{array}{*{20}{c}} {N\cos B\cos L}\\ {N\cos B\sin L}\\ {N\left( {1 - {e^2}} \right)\sin B} \end{array}} \right) $ |
| $ {r_{P'P}} = Hn = \left( {\begin{array}{*{20}{c}} {H\cos B\cos L}\\ {H\cos B\sin L}\\ {H\sin B} \end{array}} \right) $ |
可得相同基准下空间大地坐标系向空间直角坐标系转换的关系为:
| $ \left( {\begin{array}{*{20}{c}} X\\ Y\\ Z \end{array}} \right) = {r_{OP}} = {r_{OP'}} + {r_{P'P}} = \left( \begin{array}{l} \left( {N + H} \right)\cos B\cos L\\ \left( {N + H} \right)\cos B\sin L\\ \left( {N\left( {1 - {e^2}} \right) + H} \right)\sin B \end{array} \right) $ | (11) |
同理可得,相同基准下空间直角坐标系向空间大地坐标系转换的关系为:
| $ L = \arctan \frac{Y}{X} = \arcsin \frac{Y}{{\sqrt {{X^2} + {Y^2}} }} $ | (12) |
| $ B = \arctan \frac{{Z + N{e^2}\sin B}}{{\sqrt {{X^2} + {Y^2}} }} $ | (13) |
| $ H = Z\csc B - N\left( {1 - {e^2}} \right) = \sqrt {{X^2} + {Y^2}} \sec B - N $ | (14) |
由于B中还有参数B,所以采用迭代算法来计算B,取迭代初值为:
| $ {B^{\left( 0 \right)}} = \arctan \frac{Z}{{\sqrt {{X^2} + {Y^2}} }} $ | (15) |
综上分析可知,三维闪电定位误差与站网结构及闪电位置有关。在观测条件确定的前提下,站网布局决定了闪电定位误差的大小,因此选取最优化的布局方式至关重要。设定闪电发生高度为5 km,分别采用正方形、梯形、星形、不规则四边形的站网结构进行定位误差仿真,时间使用的GPS时钟精确到10-7 s,根据该定位系统的性能,把每个站收到的时间加入±0.1μs的误差,然后在定位算法里面进行仿真,其结果如图 3所示。
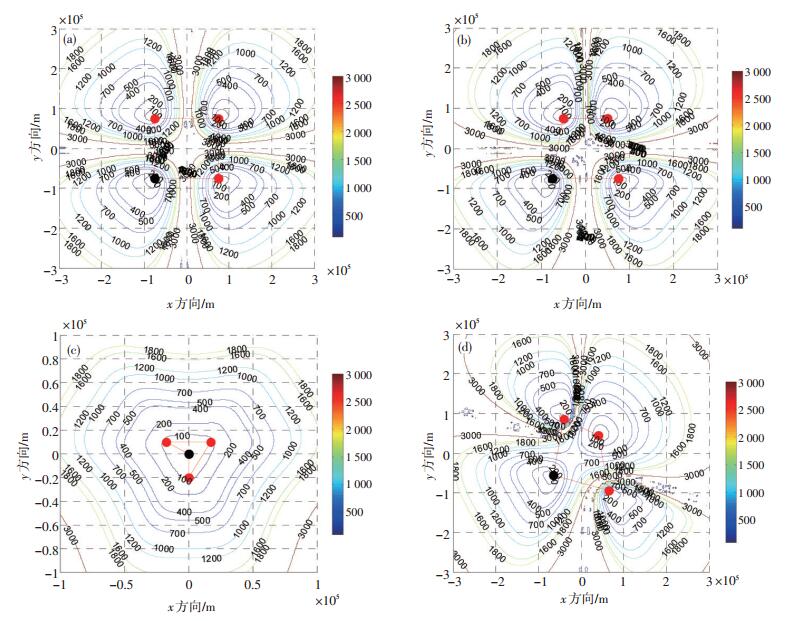
|
图 3 4种几何结构布网仿真误差(实心黑点代表主站,实心红点代表副站) (a)正方形; (b)梯形; (c)星形; (d)不规则四边形 Fig. 3 Location error simulation for the following four kinds of geometric models (Black dot represents the main station, and solid red dot represents the secondary station). (a)square, (b) trapezoid, (c) star, and (d) irregular quadrilateral |
分析图 3可知,1个主站和3个副站共同对闪电进行定位。正方形站网的探测盲区出现在正方形对称轴及其附近区域[12],在该区域的定位误差大于3 000 m。梯形布局与正方形布局有所类似,但在其中2个副站附近区域定位误差接近2 000 m。星形站网的定位精度近似以主站为中心的不规则等值圆形分布,在该布局站网内部,其定位误差小于300 m。由以上分析可知,不同的站网类型对应不同的误差分布,星形站网结构不仅定位误差呈规则分布,且定位误差小,因此在站址布局时优先选择星形站网。在实际的站址布局时,有可能受到气象观测站的制约,会出现上述不规则多边形站网结构,因此要结合具体的情况进行分析,尽可能地选取科学的布站方式。
3.2 站点布局及误差仿真湖北省三维全闪电监测定位系统由19个站点组成,在湖北省的闪电定位系统中,采用了3D-TOA定位算法。
根据上述误差分析及湖北省三维闪电定位网的站点布局情况,假定GPS时差测量误差为100 ns,传播误差为0.3 μs·(100 km)-1,随机误差在(-50 ns,+50 ns)范围,利用Matlab软件仿真闪电网定位误差(设定闪电发生高度为5 km)。
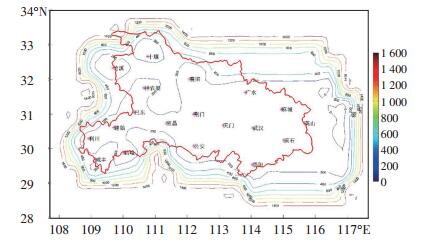
闪电的定位误差分为水平误差与高度误差,水平误差即地球表面上的经度及纬度误差,高度误差即闪电发生位置到地球表面的垂直距离误差。图 4、图 5分别给出湖北省三维闪电监测网水平定位误差、高度定位误差评估图,即水平误差分布、高度误差分布的仿真结果。分析可知,图 4中的红色边框围成的闭合图形就是湖北省的边界线,湖北省大部分地区的水平误差在200 m以内。图 5中的红色边框围成的闭合图形就是湖北省的整体构架图,可以看出湖北省大部分地区的高度误差在500 m以内,而在湖北南部区域误差较大,尤其是恩施西部及十堰西北部区域误差较大,接近1 200 m,这与此区域的站点布局有关,发生在此区域的闪电不易被探测到。
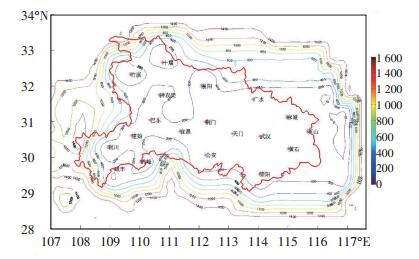
|
图 4 湖北省三维闪电监测网水平定位误差评估图(单位: m) Fig. 4 Level location error estimation of three-dimensional lightning locating network in Hubei province (unit:m). |
|
图 5 湖北省三维闪电监测网高度定位误差评估图(单位: m) Fig. 5 Height location error estimation of three-dimensional lightning locating network in Hubei province (unit:m). |
由图 4、图 5可知,高度误差约是水平误差的2~3倍,即水平定位精度要优于垂直方向上的定位精度。究其原因是,闪电水平位置经过3站定位后,可以计算出其发生的水平位置,如果第4个站也收到辐射源信息则进行一次迭代计算,从而降低误差。而高度位置至少需要4个站才能定位,如果仅通过4个站对辐射源进行定位,则闪电在高度上的定位就没有进行迭代计算以提高精度,因而高度误差相对水平定位误差较大。闪电发生的位置越靠近中心站,闪电辐射的电磁波信号就越容易被探测到,因此定位精度越高。另外,从理论上来说,定位闪电只需要4个探测站,而在实际的站点布局中,接收到同一闪电信号的探测站数量不止4个,在闪电定位计算时可以选择最优的观测数据进行优化计算,进而提高探测精度。
3.3 观测数据分析表 1给出2015年湖北地区4起雷击案例的数据。以京珠高速江夏收费站(114.311 6°E、30.309 6°N)雷击事故为例,2015年4月3日20—22时,有闪电导致江夏3#车道电涌保护器(SPD)及车检器损坏。根据表 1数据分析,最近的一次云闪高度为3.6 km,考虑该地区的高度误差为500 m,则修正后的近地面高度为3.1 km,经分析该高度的40.3 kA的闪电不足以对设备造成损坏。而对-21.7 kA地闪,按照200 m的理论误差修订后,其发生的位置距事故点近距为242.7 m,参照《交流电气装置的过电压保护和绝缘配合》DL/T620-1997中感应过电压的计算公式[14],得到在设备处的感应过电压为2.2 kV,超过电子设备的耐压(1.5 kV)能力,从而导致弱电设备的损坏。从获取的观测数据来看,观测数据与理论分析的误差较为接近,进一步说明了站网布局的合理性。
|
|
表 1 距离事故点较近的闪电数据 Table 1 Flash data nearer to the lightning accident place |
实际情况中,闪电三维定位的误差主要有4个来源:一是与闪电电磁波传播有关的误差,包括对流层影响引起传播速度的变化和地表地形的影响引起传播路径的误差[5, 13];二是与闪电探测设备相关的误差,包括闪电波形信号的提取误差和时间探测误差等,时间探测误差又包括GPS时钟误差(主要包括钟差、频偏、频漂等)和探测站时钟同步误差等[15];三是与计算有关的误差,包括探测站的坐标误差、计算模型及方法造成的误差等;四是探测站布网引起的误差,例如理想型的星型布站与更接近实际的不规则四边形布站引起的误差有所不同。
综上所述,时间探测误差和传播误差是最主要的误差来源,其他误差影响相对较小,但也不能忽略。
4 结论与讨论本文对三维闪电定位系统的4种几何布网结构及湖北省的布站结构进行了仿真分析,并通过观测数据对仿真结果做了进一步的验证,得出以下结论:
(1) 通过Matlab仿真比较了星形、正方形、梯形、不规则四边形四种几何布网结构的误差分布,得出星形布网结构探测误差最小,误差分布近似以主站为中心的不规则等值圆形分布,是最为理想的探测闪电的布网结构。
(2) 通过仿真分析可知,闪电定位网在湖北省大部分地区的水平定位误差在200 m以内,高度定位误差在500 m以内,定位误差较小,精度较高。总体来说,该布网结构具有较高的可行性。
(3) 由于站点布局的几何结构影响了恩施西部及十堰西北部区域的云闪高度探测精度,导致出现局部探测精度不高的情况。若条件允许,可采取站点加密观测的方式,进一步降低相关误差的影响,可以形成较为理想的探测效果。
由于观测数据有限,只能根据仅有的少量雷灾案例数据检验理论分析结果,实际的闪电定位误差尚需要在实践中收集更为丰富的数据后做进一步的检验。
| [1] |
叶朝谋, 俞志强. 三维时差定位系统的模糊及无解分析[J]. 现代电子技术, 2005, 212(21): 22-25. DOI:10.3969/j.issn.1004-373X.2005.21.008 |
| [2] |
俞志强, 叶朝谋. 四站三维时差定位模糊分析[J]. 空军雷达学院学报, 2009, 23(5): 370-372. DOI:10.3969/j.issn.1673-8691.2009.05.017 |
| [3] |
曾辉, 曾芳玲. 空间三站时差定位的模糊及无解问题[J]. 信息与电子工程, 2010, 8(2): 139-148. DOI:10.3969/j.issn.1672-2892.2010.02.004 |
| [4] |
廖海军.多站无源定位精度分析及相关技术研究[D].成都: 电子科技大学, 2008
|
| [5] |
张萍, 赵文光. 基于云闪的雷电定位系统的误差分析[J]. 测绘通报, 2009(1): 28-30. |
| [6] |
田彩霞, 马启明, 周晓, 等. 江苏省三维闪电定位系统算法仿真[J]. 武汉大学学报(理学版), 2014, 60(2): 115-120. |
| [7] |
禹继, 杨仲江, 陈绿文, 等. 粤港澳闪电定位系统探测效率及精确度评估[J]. 高原气象, 2015, 34(3): 863-869. |
| [8] |
邢翠柳, 陈建民. 多站无源时差定位精度分析[J]. 无线电工程, 2012, 42(2): 32-34. DOI:10.3969/j.issn.1003-3106.2012.02.010 |
| [9] |
陈渭民. 雷电学原理[M]. 北京: 气象出版社, 2006.
|
| [10] |
胡志祥.雷电定位算法和误差分析理论研究[D].武汉: 华中科技大学2012
|
| [11] |
宁津生, 刘经南, 陈俊勇, 等. 现代大地测量理论与技术[M]. 武汉: 武汉大学出版社, 2006.
|
| [12] |
William K J, Richard S J. On the retrieval of lightning radio sources from time-of arrival data[J]. J Geophys Res, 1996, 101(D21): 26631-26639. DOI:10.1029/96JD01618 |
| [13] |
聂智平, 赵文光, 文银平, 等. 雷电探测网中误差分析及相关时间同步问题研究[J]. 华中科技大学学报(城市科学版), 2007, 24(4): 33-35. DOI:10.3969/j.issn.2095-0985.2007.04.009 |
| [14] |
DL/T620-1997《交流电气装置的过电压保护和绝缘配合》[S].北京中国电力出版社
|
| [15] |
Thomas R J, Krehbiel P R, Rison W, et al. Accuracy of the lightning mapping array[J]. J Geophys Res, 2004, 109: 34. |
 2017, Vol. 36
2017, Vol. 36 