2. 湖南省怀化市气象局, 怀化 418000;
3. 湖南省靖州县气象局, 靖州 418400
2. Huaihua Meteorological Office of Hunan Province, Huaihua 418000;
3. Jingzhou Meteoroloal office of Hunan Province, Jingzhou 418400
近年来,在气候变暖和城镇化背景下,各地极端暴雨频繁发生,城市暴雨洪涝灾害已成为最突出的城市灾害, 危及城市的正常运转和公众的正常生活[1-5],如2012年北京“7.21”暴雨灾害造成70多人丧生。究其原因,一是集水区下垫面高度硬化,使汇流量加大,二是排水设施遭到破坏,三是排水系统设计标准偏低,四是近30年来城市范围不断拓宽,暴雨强度又可能变得更强,排水系统跟不上城市的发展。所以城市暴雨强度公式编制和雨型确定是排水设计标准的重要内容[6],国外诸多学者做过大量研究工作,20世纪40年代,前苏联的包高马佐娃等对乌克兰等地的降雨资料进行统计分析,划分了七种雨型[7],发现强度大致均匀的雨型很少,随着研究的发展,后来人们采用模糊识别法[8]来分析暴雨雨型; 1975年Pilgrim & cordery基于数理统计原理提出级序平均法推求暴雨雨型[9]。Knifer和Chu基于暴雨强度公式提出了峰值时刻的统计方法及峰值前后的瞬时暴雨强度计算公式-芝加哥雨型[10]。在国内,王敏等[11]使用降水资料对北京市以10 min、1 h和2 h为单位时段统计分析了120 min、12 h和24 h的设计雨型,发现各雨型间差异较大,目前还没有一种公认的雨型作为设计的依据[12]; 水利部门也常采用同频率分析法进行暴雨雨型推求[13-15]。
雨型在城市排水设计和实际业务中对掌握降雨过程的时空变化规律至关重要,其差异能直接影响降雨径流计算结果[16], 必须在大量降水资料基础上选定代表性的雨型,概括多数降雨过程的变化规律,为城市暴雨管理提供依据; 大部分文献中用1种或2种方法分析比较得出适应某地的雨型,虽然有关规范[6]暂定我国的短历时暴雨雨型为芝加哥雨型,但由于各地强降水差异较大,为探究湖南地区短历时暴雨雨型特征,应用4种雨型分析方法同时开展湖南14个地级市的暴雨雨型分型研究,并给出相对最优的分析结果,应用于湖南城市排水防涝规划设计。
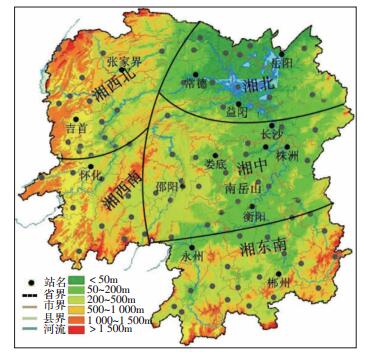
1 资料与方法 1.1 资料分析资料为湖南省14个地级城市(图 1)所在地的国家气象站1980—2013年共34 a逐分钟降雨观测资料。其中1980—2004年各站降雨原始资料为自记纸降雨资料,由湖南省气候中心使用中国气象局组织编制的“降雨自记纸彩色扫描数字化处理系统”对气象站雨量自记纸降水曲线跟踪计算,且经信息化处理,数字化转换、人工审核后的逐分钟雨量资料。2005— 2013年降雨资料为新型自动气象站自动记录的逐分钟雨量数据。
|
图 1 湖南省14个地级城市分布图 Fig. 1 Distribution of 14 cities of Hunan province. |
为使设计的雨型更具代表性,降雨时长选取按照降雨历时±15 min确定,以120 min最小降雨间隔划分的独立降雨场次中,按照降雨量从大到小排序,以降雨量大于或接近对应历时一年一遇重现期的所有降雨为参考阈值指标(表 1)。
|
|
表 1 降雨历时区间与雨量阈值 Table 1 Continuous interval and threshold of rainfall |
按表 1中的阈值指标,统计14个地级城市1980-2013年共34 a不同降雨历时(30、60、90、120、150、180 min),以5 min为间隔分段的大于或接近阈值指标的降雨场次(14—21不等)。
1.3 模糊识别法原理模糊模式识别法是用时段雨量占总雨量的比例作为该场降雨的雨型指标,建立7种雨型(图 2)的模式矩阵。再分别计算每场实际降雨与7种雨型模式的贴近度,由择近原则判断该场降雨属于哪种型式。

|
图 2 模糊识别法雨型 Fig. 2 The rainfall pattern of fuzzy recognition method. |
把雨峰时段放在出现可能性最大的位置上,而雨峰时段在总雨量中的比例取各场降雨雨峰所占比例的平均值,其它各时段的位置和比例也用同样方法确定。具体步骤如下:
(1) 选取一定历时的大雨的样本; (2)将历时分为数个小时段,时段长短取决于所期望的时程分布时间步长,一般越小越好(大部分取5 min); (3)针对选取的每场降雨,根据各时段雨量由大到小确定序号,大雨量对应小序号,将每个对应时段的序号取平均值,取值由小到大分别确定为雨强由大到小的顺序; (4)计算每个时段降雨量与总雨量的比值,取平均值; (5)以确定的最大可能次序(步骤3)和确定的分配比例(步骤4)为前提,构成雨量过程曲线。
1.5 同频率法原理同频率分析法的思路:长历时雨型包含短历时雨型,即给定各短历时峰值位置,从最长历时雨型中可以依次提取出所需各短历时雨型,保证了各历时间的关联性。具体步骤:首先需要确定峰值位置和5 min放大值。峰值位置采用所取样本峰值的平均位置,5 min的放大值为所取样本5 min最大值的平均值,其余时段按比例分配。2 h历时将1 h雨型根据峰值位置对齐放入,其余时段按比例分配,其它时段依次类推,最终得到24 h设计雨型。
1.6 芝加哥法原理芝加哥雨型的确定由综合雨峰位置系数、降雨过程线模型两部分组成。
综合雨峰位置系数是据每场降雨峰值时刻与整个历时的比值而统计确定; 对历时相同暴雨过程求出雨峰位置系数平均值,将各历时雨峰位置系数按照各历时的长度进行加权平均。
令峰前的瞬时强度为i(tb),相应历时为tb,峰后的瞬时强度为i(ta),相应历时为ta。取一定重现期下暴雨强度公式形式为:i=A/(t+b)n,雨峰前后瞬时降雨强度可由下两式计算:
| $ i({t_{\rm{b}}}) = A{[(1-n){t_{\rm{b}}}/r + b\left] / \right[{t_{\rm{b}}}/r + b]^{n + 1}} $ | (1) |
| $ i({t_{\rm{a}}}) = A{[(1-n){t_{\rm{a}}}/(1-r) + b\left] / \right[{t_{\rm{a}}}/(1-r) + b]^{n + 1}} $ | (2) |
式中,A、b、n为一定重现期下暴雨强度公式中的参数,r为综合雨峰位置系数(0~1)。利用公式i(tb)、i(ta)计算芝加哥合成暴雨过程线各时段(5 min)的累积降雨量及各时段的平均降雨量,得到每个时段内平均降雨强度,确定出对应一定重现期及降雨历时芝加哥法雨型[17]。
2 结果分析 2.1 模糊识别结果根据表 1提取14个地市州降水资料,按原理分析并汇总, 得到模糊雨型统计比例(表 2),从表中可见:(1)湖南单峰型占82.1%,双峰型9.8%,均匀型8.1%;(2)单峰雨型雨峰在前部的占56.8%,中部18.6%,后部6.7%;(3)双峰雨型仅占9.8%,雨峰出现在后部没有(第5和第7类); (4)雨强大致均匀第4类仅8.1%。
|
|
表 2 模糊识别法雨型统计比例(%) Table 2 The Statistical ratio of fuzzy rainfall pattern (unit:%) |
提取资料分别对各地各历时进行雨型推求并绘图,由于版面关系,文中仅给出长沙历时60、120、180min雨型。
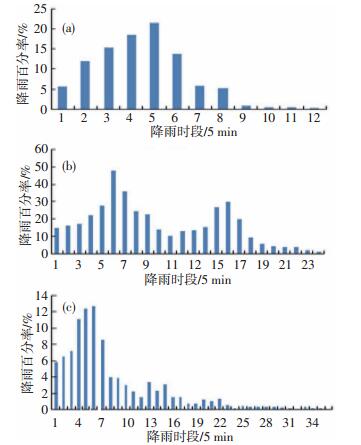
由图 3a可见,长沙市历时60 min雨峰在第5段出现,从1~5段可见雨量迅速上升,雨峰后,雨强迅速减弱; 历时120 min(图 3b)时,出现了2个峰值,第1峰在第6段,第2峰在第16段,第1雨峰及其前后的雨量比第2雨峰与前后要大; 历时180 min雨峰出现在第6段(图 3c),整个降雨过程前25 min降雨量迅速增大,峰值后,降雨量随着时间推移迅速减小,这与历时60 min的雨型较为相似。
|
图 3 长沙市不同历时(a:60 min,b:120 min,c:180 min) P&C雨型设计 Fig. 3 The rain pattern design of rainfall duration in Changsha city for (a)60 min, (b)120 min, and (c)180 min. |
从14个城市看,各地各历时除长沙、娄底、永州历时120 min为双峰型外,其余均为单峰型; 历时60、120 min设计暴雨雨型的雨峰位置略超前于整场降雨过程1/3分位,180 min处于1/3分位。
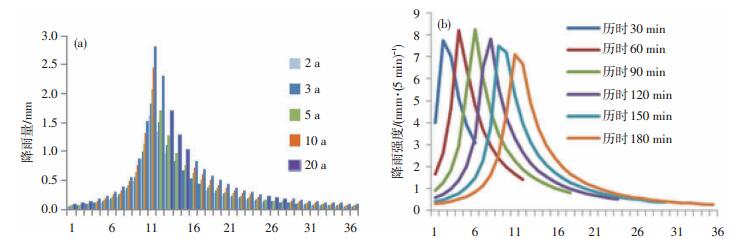
2.3 芝加哥法分析经统计确定综合雨峰位置系数后,推求了各地各历时暴雨雨型。以长沙历时180 min重现期2 a、3 a、5 a、10 a、20 a为例(图 4a),雨峰位置在第11段,随着重现期的增加,雨峰强度也随之增强; 从重现期2 a各历时的雨型(图 4b)来看,随着历时的增加,雨峰位置处的强度呈现“增大-减小”的波动趋势,差异较小,雨峰最大值出现在历时90 min,5 min最大峰值8.25 mm。从14个城市各历时雨型图看,各历时暴雨雨峰位置基本上处于整场降雨1/3分位,降雨强度随重现期的延长而增大; 相同重现期下,雨峰位置处的降雨强度随历时的增加呈现“增大-减小”的波动趋势,但差异较小。
|
图 4 长沙市历时180 min各重现期芝加哥暴雨雨型(a)和长沙市重现期2 a各历时芝加哥暴雨雨型(b) Fig. 4 Rainstorm pattern by Chicago method in Changsha city for (a) the reappearing period of duration of 180 min, and (b) all rainfall durations of 2 a reappearing period. |
采用同频率法分析的结果见表 3,从表 3可以看出:各地各历时雨峰位置非常集中,历时60 min雨峰位置处于整场降雨的1/2分位,历时120 min处1/3分位略滞后,历时180 min处于1/3分位。
|
|
表 3 同频率法得出的各地5 min雨峰位置(时段序号) Table 3 Rain peak position of 5 min by the same frequency method |
如将雨型全部绘成图(略),可以看到:各地各历时雨型几乎一样,全为单峰型,所不同的就是雨峰强度有所变化,雨峰位置前后略有移动。
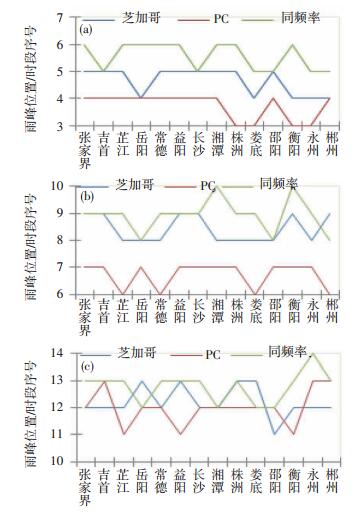
3 对比分析 3.1 雨峰位置比较从峰值位置(图 5)看,不同方法推求的各地各历时暴雨雨型雨峰位置较为接近。从各地历时60、120 min雨峰位置可以看出,芝加哥法趋于P&C法、同频率法二者之间,落后(超前)P&C法(同频率法)一个时距(5min); 历时180 min各地平均位置三者非常接近,平均相差不到1个时距。
|
图 5 湖南各站点不同分析方法得出的60 min (a), 120 min(b)及180 min (c)历时的雨峰位置 Fig. 5 The peak position of rainfall durations of (a) 60 min, (b) 120 min, and (c) 180 min for different method. |
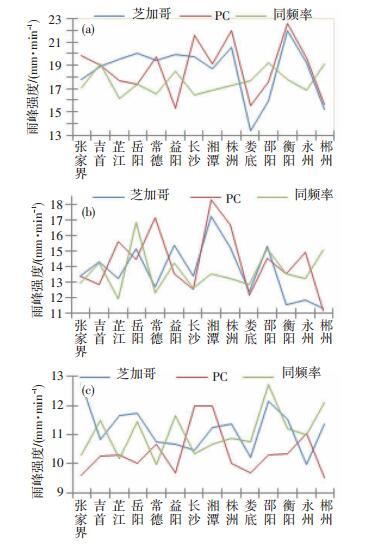
从雨峰峰值强度(图 6)看,随着历时的延长,雨峰强度也随之减弱,P&C法峰值略大于芝加哥峰值,同频率法偏弱,均能较好地反映峰值强度。相对而言,历时60、120 min同频率法峰值强度较为平稳,振幅较小,另外2种方法的峰值更为接近,历时180 min芝加哥雨峰强度与同频率法峰值更相近,P&C法偏弱。
|
图 6 湖南各站点不同分析方法得出的60 min (a), 120 min (b)及180 min (c)历时的峰值强度 Fig. 6 The peak intensity of rainfall durations of (a)60 min, (b)120 min, and (c)180 min for different methods. |
从峰值位置和强度对比看,P&C与芝加哥雨型均可应用于湖南短历时暴雨雨型设计,而同频率法相对来说略显不足。
4 结论利用4种方法对湖南14个地市所在地的短历时暴雨雨型进行了分析,得出如下结论:
(1) 通过模糊识别法,湖南单峰雨型占82.1%,双峰雨型占9.8%,均匀雨型8.1%。
(2) Pilgrim & Cordery分析表明:在各地各历时除长沙、娄底、永州历时120 min为双峰型外,其余均为单峰型; 历时60、120 min设计雨型的雨峰位置略超前于1/3分位,历时180 min处于1/3分位。
(3) 芝加哥法分析表明:各历时的降雨强度,随着重现期的延长而增大; 相同重现期下,随着历时的增加,雨峰位置处的降雨强度随历时的增加呈现“增大-减小”的波动趋势,差异较小; 雨峰位置基本上处于整场降雨的1/3分位。
(4) 同频率法分析表明:各地市历时雨型全为单峰型; 雨峰位置非常集中,历时60 min处于1/2分位,历时120 min比1/3分位略滞后,历时180 min处于1/3分位。
(5) P&C与芝加哥雨型推求的各历时大部分暴雨雨型基本一致,比较接近实际,均可用于湖南短历时暴雨雨型设计,但基于以后研究中与其他地区的一致性以及计算的便捷性考虑,仍建议工程设计者使用《城市暴雨强度公式编制和设计暴雨雨型确定技术导则》上推荐的芝加哥法得到的短历时暴雨雨型结果来进行实际使用[17]。
(6) 多种方法推求的各地各历时雨型基本以峰值在前部的单峰型为主,关注各场降雨的1/3分位处的强降雨,因它降雨量集中,易引起较大洪水,说明在较短时间内对城区排水能产生较大影响。
致谢:该文写作过程中得到陈正洪正研级高工的悉心指导,谨致谢意。
| [1] |
孙佳, 郭渠.重庆市主城区设计暴雨雨型编制报告[R].2014
|
| [2] |
李书严, 马京津, 轩春怡, 等. 1951—2008年北京极端天气事件分析[J]. 气候与环境研究, 2012, 17(2): 244-250. |
| [3] |
王强. 北京市城市暴雨内涝原因分析和对策建议[J]. 给水排水, 2014(s1): 127-130. |
| [4] |
孙继松, 何娜, 王国荣, 等. 7.21"北京大暴雨系统的结构演变特征及成因初探[J]. .暴雨灾害, 2012, 31(3): 218-225. |
| [5] |
黄会明, 邓丽, 王立宏, 等. 城市设计暴雨和设计雨型的推求及应用[J]. 中国农村水利水电, 2014(3): 35-37. |
| [6] |
城市暴雨强度公式编制和设计暴雨雨型技术导则[M].北京: 气象出版社, 2014
|
| [7] |
莫洛可夫, M B, 施果林. 雨水道与合流水道[M]. 北京: 建筑工程出版社, 1956.
|
| [8] |
吴介一, 张飒兵, 张孝林, 等. 计算机网络中面向拥塞控制的一种模糊流量控制机制[J]. 东南大学学报:自然科学版, 2001, 31(1): 6-10. |
| [9] |
Pilgrim D H, Cordery I. Rainfall temporal patterns for design floods[J]. Journal of the Hydraulics Division, ASCE, 1975, 101(1): 81-95. |
| [10] |
Keifer G J, Chu H H. Synthetic storm pattern for drainage desig[J]. Journal of the Hydraulics Division, ASCE, 1957, 83(4): 1-25. |
| [11] |
王敏, 谭向诚. 北京城市暴雨和雨型的研究[J]. 水文, 1994(3): 1-6. |
| [12] |
岑国平, 沈晋, 范荣生, 等. 城市设计暴雨雨型研究[J]. 水科学进展, 1998, 9(1): 41-46. DOI:10.3321/j.issn:1001-6791.1998.01.007 |
| [13] |
牟金磊.北京市设计暴雨雨型分析[D].兰州: 兰州交通大学, 2011
|
| [14] |
宁静.上海市短历时暴雨强度公式与设计雨型研究[D].上海: 同济大学, 2006.
|
| [15] |
霍勇峰. 山西省设计暴雨雨型分析[J]. 水资源与水工程学报, 2011, 22(6): 158-161. |
| [16] |
王彬雁, 赵琳娜, 巩远发, 等. 北京降雨过程分型特征及短历时降雨重现期研究[J]. 暴雨灾害, 2015, 34(4): 302-308. DOI:10.3969/j.issn.1004-9045.2015.04.002 |
| [17] |
成丹, 陈正洪, 方怡. 宜昌市区短历时暴雨雨型特征[J]. 暴雨灾害, 2015, 34(3): 249-253. DOI:10.3969/j.issn.1004-9045.2015.03.007 |
 2017, Vol. 36
2017, Vol. 36 