2. 中国人民解放军国防科学技术大学海洋科学与工程研究院,长沙 410073
2. Institute of Ocean Science and Engineering, National University of Defence Technology, Changsha 410073
数值模式动力框架核心是空间离散化和时间积分方案, 它决定模式描述大气运动数学特性、物理保守性和计算稳定性。
谱模式以欧洲中期天气预报中心(ECMWF)为代表。周毅等[1]认为, 谱(球谐函数)具备对原函数"收敛性"和"最优性"(最小平方误差逼近), 但作二维谱展开仍存在一些数学与计算缺陷:谱展开存在波数截断误差, 在洋面上存在虚假的谱地形波(Gibbs现象), 矢量场(水平风及加速度场)在极点为数学奇点(实际谱展开关于极点不对称), 模式垂直格式不适合于谱, 且谱不适合做中尺度数值模式, 另外, 若提高谱模式空间分辨率, 谱计算量将迅速增加, 其提高模式精度效率迅速降低。自20世纪90年代末以来, 世界上一些国家(如英国、美国、加拿大、法国、日本和中国)重新转向研究水平分辨率从1~100km的全球/区域统一(格点)数值模式[2-5]。但是, 格点模式同样遇到一些数学困难:经纬网格存在极区网格点过密与极点奇异, 欧拉差分, 其时间积分受制于CFL计算稳定性条件等。
我国自主研究开发的GRAPES全球/区域统一数值模式[5], 采用经纬网格与半隐式-半拉格朗日积分方案(semi-implic semi-Lagrangian integration scheme, 简称SI_SL方案)[6-8], 但必须求解庞大计算量的"三维气压扰动"广义共轭余差Helmholtz方程, 即采用Ritche[7]计算拉格朗日上游点(Lagrangian particle)路径方案, 在极区采用McDonald & Bates[9]旋转格点计算上游点路径方案, 但不对极点作预报。陈德辉等[10]认为, 空间差分截断误差比时间差分截断误差大得多, 采用拉格朗日差分方案不仅可以提高空间差分计算精度, 且使其时间步长只依据拉格朗日差分方案计算精度, 而不再依据欧拉差分方案计算稳定度, 故其在静力/非静力模式中得到广泛应用。
HUANG Bo等[11]认为, GRAPES模式采用Lagrangian三次函数插值(双线性插值)计算准拉格朗日平流(quasi-Lagrangian advection, 以下简称SL_CL方案), 因双线性插值具有一定"阻尼"效应, 使得SL_CL方案计算精度较低, 因而基于Reich平流方案[8](以下简称R2007方案), 提出所谓"双三次B样条+双线性B样条插值方案(简称Re_R2007方案):对于双三次B样条16点插值之后所形成的误差矩阵, 又做双线性B样条4点插值补充(这种考虑很值得借鉴), 并经过局地直角坐标均匀网格1维正弦波和2维余弦"杯"波理想试验, 去比较SL_CL方案和Re_R2007方案, 因后者明显减少"阻尼"效应, 其标准误差可成倍减少, 从而表明后者比前者具有较高的计算精度, 之后又做球面坐标非均匀网格固体旋转试验, 也证明存在这个结论。但在数学上, 除了可以采用三次B样条基函数求解(插值)方法, 还可采用三次样条函数拟合(插值)方法, 二者的差别在于, 后者完全经过控制点(承认控制点值), 前者仅经过两个端点并受其它控制点制约, 即前者不经过其它控制点(不承认其它控制点值), 则B样条插值隐含一定的平滑, 而平滑的数学功能是"舍精度换稳定"。
本文借鉴谱模式动力框架核心思想, "高斯网格二维谱变换半隐式-半拉格朗日积分方案", 研究"准均匀经纬网格三次样条函数变换(变换=拟合+插值, 以下简称'样条变换')显式-准拉格朗日积分方案"。应该指出, 高斯网格(网格点从赤道向两极减少)属于一种准均匀经纬网格。周毅等[1]认为, 因水平矢量场为二元量"场, 对水平矢量场作谱展开在极点为数学奇点, 则是谱展开不能包含极点(实际选点偏于极点), 故谱展开关于极点不对称。本文将设计一种准均匀经纬网格, 并且通过样条变换, 试图克服极区网格点过密与极点奇异问题。
三次样条函数属于Hermite二重密切(二阶可导)拟合+插值"[12]:三次样条函数分为"线、面、体", 即三次样条(cubic spline)、双三次曲面(bi-cubic surface)[13]和三次曲体(tri-cubic cube), 而以三次样条(样条格式)为数学基础。
样条格式是以"3点"为主但关于全局(全部格点)的"二阶可导"非线性格式。对于离散等距ΔX变量场Pj, j=0,±1,±2,...,三次样条斜率mj和曲率Mj与一阶中央差${{\bar m}_j}$和二阶中央差${{\bar M}_j}$有如下数学关系(样条格式与中央差数学关系)[12]:
| $ \begin{array}{l} {{\bar m}_j} = {m_j} + \frac{{{m_{j + 1}} - 2{m_j} + {m_{j - 1}}}}{6} = \frac{{{P_{j + 1}} - {P_{j - 1}}}}{{2\Delta X}}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {一阶中央差} \right)\\ {{\bar M}_j} = {M_j} + \frac{{{M_{j + 1}} - 2{M_{j - 1}}}}{6} = \frac{{{P_{j + 1}} - 2P + {P_{j - 1}}}}{{\Delta {X^2}}}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {二阶中央差} \right) \end{array} $ |
两式表明, 中央差斜率和曲率分别就是三次样条斜率和曲率作系数为1/3的"三点平滑", 故中央差近似总是减小大气波动振幅和减慢其波速[1]。同时, 样条格式曲率Mj的"线性部分"就是二阶中央差${{\bar M}_j}$, 而样条格式斜率mj是由曲率Mj决定(二者不独立)[12]。因${{\bar M}_j}$格式比${{\bar m}_j}$格式空间分辨率高一倍, 可以证明, 前者截断误差及波速和群速误差均为后者的一半, 例如, 波长为4ΔX的${{\bar M}_j}$格式与波长为8ΔX的${{\bar m}_j}$格式空间分辨率及截断误差一致, 从而可以认为, 样条格式计算精度高于一阶、二阶中央差。
三次样条具有数学定律(可推广到三次曲面和曲体)[12]:
(1) 三次样条及其1阶、2阶导数收敛于原函数及其1阶、2阶导数(收敛性);
(2) 三次样条二阶导数对原函数二阶导数为最佳逼近(最优性);
(3) 三次样条既是二阶空间精度差分格式(精确性), 又是二阶可导积分格式(可积分性);
(4) 存在周期三次样条函数(周期性);
(5) 自然三次样条函数具有最小总曲率(趋稳性);
(6) 存在多种三次样条数学边界(边界适应性);
(7) 存在三次样条光顺泛函数(可光顺性), 以消除多余拐点"(二拐点)和不连续"尖点"或"环绕"(二重合点);
(8) 三次样条可保持点对称性(关于极点、经向、纬向对称), 而双三次曲面可保持球(面)对称性(关于极点、经向、纬向、经圈和赤道对称);
(9) 三次样条可拼接其它连续函数(拼接性), 如三次样条可拼接二次、线性函数(无Gibbs现象)。
样条格式将表明, "双三次曲面+三次样条"适合于做全球静力数值模式, 而"三次曲体"适合于做"立方体"非静力数值模式, 即样条格式完全适合做全球统一(格点)数值模式(以下称"样条模式")。则样条模式既是格点模式的可能发展方向, 又能够克服谱模式既有的数学缺点。
还应指出, 前述Lagrangian三次函数插值、双三次B样条插值[14]和上述Hermite三次样条函数插值, 虽然三者具有数学相似性(均是三次函数), 但后者的数学要求最高。例如做二维插值, 前二者都可以做16点插值, 而后者还必须已知该16点组成"曲面"的边界条件(边界斜率1阶导数或曲率2阶导数), 其可概括为著名的(由4点组成) Hermite双三次曲面片(Hermite bicubic patch)[14], 即必须已知该曲面片的4个角点值及4个纬向斜率、4个经向斜率和4个水平挠率(2阶混合偏导数, 它通过纬向-经向重叠三次样条拟合得到, 进而可拟合变量场的3阶混合偏导数, 它通过纬向-经向-垂直方向三重三次样条拟合得到)[15], 因其考虑了变量场挠率, 故其计算精度最高。但因任何变量场都不是三次函数"拟合就能完美实现的, 况且对同元预报变量可以取不同的数学与物理形式, 例如模式可以对气压、气温做预报, 而GRAPES模式是对Exner气压与位温做预报, 因而同元变量场的斜率、曲率和挠率都为之改变, 模式的这一变更特性通过数学解析曲线(正弦线)和曲面(余弦"杯")理想试验并不一定能够得到验证, 因解析曲线、曲面具有解析的"定常"斜率、曲率和挠率。
吕美仲等[16]采用样条格式对正压原始方程做欧拉差分半隐式积分方案, 经试验于一维平流方程证明, 样条格式计算精度高于中央差二阶、四阶格式精度, 给出一种用三次样条函数求解Helmholtz方程迭代法, 证明迭代具有收敛性, 给出计算个例表明, 样条格式较中央差格式更为稳定, 可较少使用平滑, 其预报波振幅和波相速较为准确。Anita[17]在球面坐标上, 采用样条格式对浅水波方程做欧拉差分半隐式"蛙跳"三时间层积分方案, 经积分试验表明, 它是一种高阶(三次)精确且计算稳定的方法, 相比之下, 谱方法将遇到高阶勒让德变换复杂性。辜旭赞等[18-19]研究采用三次样条函数变换, 做"经纬网格-准均匀经纬网格"切换插值, 即实现样条格式求经纬网格上游点, 上游点气块被限定在样条格式斜率、曲率和挠率之变量场上运动(所谓"三次运动"), 同时克服极区网格点过密和极点奇异经典问题。辜旭赞[15, 20]用泰勒级数展开, 完成四阶时空余差准拉格朗日法和欧拉法对接推导, 证明用三次样条函数插值求拉格朗日上游点路径、或设计样条斜率、曲率和挠率格式求欧拉法位移, 两种方法的数学基础完全一致, 同为二阶时空精度数值解, 也可以去求四阶时空精度的数值解, 但三次样条拟合计算量将呈指数增长。
研究"双三次曲面插值准拉格朗日平流方案", 同样需要一套国内外认可、有效、可对比的方法, 验证其可行性、精确性及程序正确性。理想场试验是国内外同行认可的普遍方法, 因提出各种理想场试验参考解(Benchmark标准解)[21-23], 用以检验新方案积分数值解的一致性、收敛性和稳定性。一般做法是:设计满足某种动力学约束、解析的初值场, 关闭与该动力过程无关因子, 对该理想场做新方案时间积分, 检验其基本性能。Williamson[24]提出用于检验全球浅水波模式的一套理想场试验方法, 认为其中的平衡流试验是检验准拉格朗日时间积分的有效方法; Galewsky[25]对illiamson的检验方案做了改进; 左瑞亭等[26]对全球大气环流模式(IAP AGCM-Ⅲ)做了Rossby-Haurwitz波试验。杨学胜等[27, 28]对GRAPES全球模式做了经纬网格求上游点路径的平衡流试验和极区旋转格点求上游点路径的过极地气流试验, 认为准拉格朗日平流方案较难准确求得极区和极点的上游点。
1 样条格式预报方程 1.1 大气运动方程球面坐标"薄层大气"原始大气运动方程为(设为无地形、无水汽源汇, 并设时间t, 气压p、气温T、比湿q、V=(u,v,w)为三维风场, λ(λ ∈[0,2π])、ϕ(ϕ ∈[-π/2,π/2])分别为经、纬度, r=(r0+z)是气块至地心距离, r0为地球平均半径, 则δx=r0cosϕδλ, δy=r0δϕ, δr=δz, 以及$f$=2Ωsinϕ、$\tilde f$=2Ωcosϕ、Ω为地球自转角速度, R=Rd(1+0.618q), Rd、R分别为干、湿空气比气体常数, Cp为湿空气定压比热, 并设κ=R/Cp, g为地球重力常数, F为摩擦力, "="为定义符号):
| $ \frac{{{\text{d}}v}}{{{\text{d}}t}} = - RT\frac{{\partial \ln p}}{{\partial x}} + fv - \tilde fw + \frac{{uv \cdot \tan \phi - uw}}{{{r_0}}} + {F_u} = {a_u} $ | (1) |
| $ \frac{{{\text{d}}v}}{{{\text{d}}t}} = - RT\frac{{\partial \ln p}}{{\partial y}} - fu - \frac{{{u^2}\tan \phi + vw}}{{{r_0}}} + {F_v} = {a_v} $ | (2) |
| $ \frac{{{\text{d}}w}}{{{\text{d}}t}} = - RT\frac{{\partial \ln p}}{{\partial z}} - g + \tilde fu + \frac{{{u^2} + {v^2}}}{{{r_0}}} + {F_w} = {a_w} $ | (3) |
| $ \frac{{{\text{d}}\ln p}}{{{\text{d}}t}} = \frac{{ - 1}}{{1 - k}}\nabla \cdot V = {a_p} $ | (4) |
| $ \frac{{{\text{d}}\ln T}}{{{\text{d}}t}} = \frac{{ - k}}{{1 - k}}\nabla \cdot V = {a_T} $ | (5) |
| $ \frac{{{\text{d}}q}}{{{\text{d}}t}} = 0 $ | (6) |
因u与u方程在极点无定义, 而v与v方程在极点有定义, 则先定义北、南极点(分别用下标N和S表示)与0°E的u平行分量为uN和uS, 而与0°E的v平行分量为vN和vS。那么, 在北、南极点, 对于任何水平矢量, 如(uN,vN)和(uS,vS), 都可作如下的三角函数矢量分解:
| $ \begin{array}{l} {u_{N\left( \lambda \right)}} = {u_N}\cos \lambda + vN\sin \lambda ;{u_{N\left( \lambda \right)}} = {v_N}\cos \lambda - {u_N}\sin \lambda \\ {u_{S\left( \lambda \right)}} = {u_N}\cos \lambda - {v_S}\sin \lambda ;{v_{S\left( \lambda \right)}} = {v_S}\cos \lambda + {u_S}\sin \lambda \end{array} $ | (7) |
容易证明, 上式有uN=uN(0)≡vN(3π/2)和uS=uS(0)≡vS(π/2), 同理, 有水平矢量${\left({\frac{{\delta \ln p}}{{\delta x}}} \right)_N} \equiv {\left({\frac{{\delta \ln p}}{{\delta y}}} \right)_{N\left({3\pi /2} \right)}}$和${\left({\frac{{\delta \ln p}}{{\delta x}}} \right)_S} \equiv {\left({\frac{{\delta \ln p}}{{\delta y}}} \right)_{S\left({\pi /2} \right)}}$。北、南极点v方程都是由v方程(2)式取$\phi \to \pm \frac{\pi }{2}$得到,其中$\mathop {\lim }\limits_{\phi \to \pm \frac{\pi }{2}} {u^2}\tan \phi = \mathop {\lim }\limits_{\phi \to \pm \frac{\pi }{2}} {\left({\frac{{{r_0}\cos \phi d\lambda }}{{dt}}} \right)^2}\tan \phi = \mathop {\lim }\limits_{\phi \to \pm \frac{\pi }{2}} r_0^2{\left({\frac{{d\lambda }}{{dt}}} \right)^2}\cos \phi \sin \phi = 0{\text{ }}$(高阶无穷小项), 而uN方程和uS方程分别由vN方程和vS方程沿地球轴顺时针旋转90°得到。即两极点水平运动方程为:
| $ \frac{{{\text{d}}{u_N}}}{{{\text{d}}t}} = - RT{\left( {\frac{{\delta \ln p}}{{\delta y}}} \right)_{N\left( {3\pi /2} \right)}} + f{v_N} - \frac{{{u_N}w}}{{{r_0}}} + {F_v} $ | (8) |
| $ \frac{{{\text{d}}{u_S}}}{{{\text{d}}t}} = - RT{\left( {\frac{{\delta \ln p}}{{\delta y}}} \right)_{S\left( {\pi /2} \right)}} + f{v_s} - \frac{{{u_s}w}}{{{r_0}}} + {F_v} $ | (9) |
| $ \frac{{{\text{d}}{u_N}}}{{{\text{d}}t}} = - RT{\left( {\frac{{\delta \ln p}}{{\delta y}}} \right)_{N\left( 0 \right)}} + f{u_N} - \frac{{{v_N}w}}{{{r_0}}} + {F_v} $ | (10) |
| $ \frac{{{\text{d}}{u_S}}}{{{\text{d}}t}} = - RT{\left( {\frac{{\delta \ln p}}{{\delta y}}} \right)_{S\left( 0 \right)}} + f{u_S} - \frac{{{v_S}w}}{{{r_0}}} + {F_v} $ | (11) |
设P表示p、T、q、u、v、w等, 已知P的一阶时间全导数(变率)为$\frac{{{\text{d}}P}}{{{\text{d}}t}} = a$, 对于u、v、w方程, 其变率(au,av,aw)为旋转地球上单位质量空气所受广义牛顿力(加速度), 它们是"气压梯度力+重力+地转偏向力+曲率力+摩擦力"合力的三个分力; 对于p、T方程, 其变率(ap,aT)为三维散度造成的绝热变率; 对于q方程, 其变率(aq)为水汽源汇及相变变率, 干绝热时其为零。
设欧拉点(x,y,z)预报变量为P(t+Δt,x,y,z), Δt为时间步长, 且设P的二阶时间变率为$\frac{{{{\text{d}}^2}P}}{{{\text{d}}{t^2}}}\left({ = \frac{{{\text{d}}a}}{{{\text{d}}t}}} \right) = a'$ (${a'}$一般为未知), 而P的三阶以上时间变率均为零, 则有"二阶时间变率"准拉格朗日预报方程:
| $ \begin{gathered} P\left( {t + \Delta t, x, y, z} \right) = P\left( {t, x - \Delta x, y - \Delta y, z - \Delta z} \right) + \hfill \\ \left( {t, x - \Delta x, y - \Delta y, z - \Delta z} \right)\Delta t + a'\left( {t, x - \Delta x, y - \Delta y, z - \Delta z} \right)\frac{{\Delta {t^2}}}{2} \hfill \\ \end{gathered} $ | (8) |
上式三维上游点P(t,x-Δx,y-Δy,z-Δz)仅取泰勒级数"二阶空间余差"近似:
| $ \begin{gathered} P\left( {t,x - \Delta x,y - \Delta y,z - \Delta z} \right) \approx P\left( {t,x,y,z} \right) - \Delta x\frac{{\delta P}}{{\delta x}} \hfill \\ - \Delta y\frac{{\delta P}}{{\delta y}} - \Delta z\frac{{\delta P}}{{\delta z}} + + \frac{{{\Delta ^2}x}}{2}\frac{{{\partial ^2}P}}{{\partial {x^2}}} + \frac{{{\Delta ^2}y}}{2}\frac{{{\partial ^2}P}}{{\partial {y^2}}} + \frac{{{\Delta ^2}z}}{2}\frac{{{\partial ^2}P}}{{\partial {z^2}}} \hfill \\ + \Delta x\Delta y\frac{{{\partial ^2}P}}{{\partial x\partial y}} + \Delta x\Delta z\frac{{{\partial ^2}P}}{{\partial x\partial z}} + \Delta y\Delta z\frac{{{\partial ^2}P}}{{\partial y\partial z}} \hfill \\ \end{gathered} $ | (9) |
同理(9)式, 可以给出上游点1、2阶时间变率a和${a'}$。
并按牛顿加速度定律, 求取"二阶时间余差"上游点三维运动路径(位移)(Δx,Δy,Δz), 同时确定上游点三维坐标(x-Δx,y-Δy,z-Δz):
| $ \begin{array}{l} \Delta x = u\left( {t, x - \Delta x, y - \Delta y, z - \Delta z} \right)\Delta t + {a_u}\left( {t, x - \Delta x, y - \Delta y, z - \Delta z} \right)\frac{{\Delta {t^2}}}{2}\\ \Delta y = v\left( {t, x - \Delta x, y - \Delta y, z - \Delta z} \right)\Delta t + {a_v}\left( {t, x - \Delta x, y - \Delta y, z - \Delta z} \right)\frac{{\Delta {t^2}}}{2}\\ \Delta z = w\left( {t, x - \Delta x, y - \Delta y, z - \Delta z} \right)\Delta t + {a_w}\left( {t, x - \Delta x, y - \Delta y, z - \Delta z} \right)\frac{{\Delta {t^2}}}{2} \end{array} $ | (10) |
实际应采用迭代法计算上游点位移(坐标)及其物理量, 迭代初值不妨就取u(t,x,y,z)、v(t,x,y,z)、w(t,x,y,z)、au (t,x,y,z)、av(t,x,y,z)、aw(t,x,y,z)。
1.3 样条格式二阶时空离散预报方程因三次样条函数具有数学定律"二阶可导'收敛性'和'最优性'"及适当三次样条边界, 故采用三次样条函数拟合去求解完全"二阶时空余差"三维上游点(9)-(10)式。即做变量(P)场三次样条函数拟合, 实现P场"线、面、体"二阶可导, 求得斜率Px、Py、Pz, 曲率Pxx、Pyy、Pzz和挠率Pxy、Pxz、Pyz (挠率由正交双向(如纬向-经向)重叠三次样条拟合得到)。所谓"样条格式"即认为(9)式中:$\frac{{\delta P}}{{\delta x}} \approx {P^x}, \frac{{\delta P}}{{\delta y}} \approx {P^y}, \frac{{\delta P}}{{\delta z}} \approx {P^z}, \frac{{{\delta ^2}P}}{{\delta {x^2}}} \approx {P^{xx}}, \frac{{{\delta ^2}P}}{{\delta {y^2}}} \approx {P^{yy}}, {\text{ }}\frac{{{\delta ^2}P}}{{\delta {z^2}}} \approx {P^{zz}}, \frac{{{\delta ^2}P}}{{\delta x\delta y}} \approx {P^{xy}}, \frac{{{\delta ^2}P}}{{\delta x\delta z}} \approx {P^{xz}}{\text{ }}$和$\frac{{{\delta ^2}P}}{{\delta y\delta z}} \approx {P^{yz}}$则(9)式近似变为三次曲体插值三维上游点(设为):
| $ \begin{gathered} P\left( {t, x - \Delta x, y - \Delta y, z - \Delta z} \right) \approx P\left( {t, x, y, z} \right) - \Delta x{P^x} - \hfill \\ \Delta y{P^y} - \Delta z{P^z} + + \frac{{\Delta {x^2}}}{2}{P^{xx}} + \frac{{\Delta {y^2}}}{2}{P^{yy}} + \frac{{\Delta {z^2}}}{2}{P^{zz}} + + \Delta x\Delta y{P^{xy}} + \hfill \\ \Delta x\Delta z{P^{xz}} + \Delta y\Delta z{P^{yz}} = \dddot P\left( {t, x - \Delta x, y - \Delta y, z - \Delta z} \right) \hfill \\ \end{gathered} $ | (11) |
若(11)式略去水平-垂直挠率Pxz和Pyz高阶小项, 但保留经向-纬向挠率Pxy项, 其变为:
| $ \begin{gathered} \dddot P\left( {t, x - \Delta x, y - \Delta y, z - \Delta z} \right) \approx P\left( {t, x, y, z} \right) - \Delta x{P^x} - \Delta y{P^y} \hfill \\ - \Delta z{P^z} + \frac{{\Delta {x^2}}}{2}{P^{xx}} + \frac{{\Delta {y^2}}}{2}{P^{yy}} + \frac{{\Delta {z^2}}}{2}{P^{zz}} + + \Delta x\Delta y{P^{xy}} \hfill \\ = \dddot P\left( {t, x - \Delta x, y - \Delta y, z - \Delta z} \right) - \Delta z{P^z} + \frac{{\Delta {z^2}}}{2}{P^{zz}} \hfill \\ \end{gathered} $ | (12) |
上式$\dddot P\left({t, x - \Delta x, y - \Delta y, z - \Delta z} \right)$为双三次曲面插值水平上游点, (12)式是"水平双三次曲面+垂直三次样条降阶插值先求${\dddot P}$, 代替(11)式三次曲体插值求${\dddot P}$。但(11)式计算量含水平三次样条Px、Py、Pxy和垂直三次样条Pz、Pxz、Pyz, 而(12)式计算量减少Pxz和Pyz。
从而有样条格式准拉格朗日二阶时空余差预报方程:
| $ \begin{gathered} P\left( {t + \Delta t, x, y, z} \right) = \dddot P\left( {t, x - \Delta x, y - \Delta y, z - \Delta z} \right) + \hfill \\ \dddot a\left( {t, x - \Delta x, y - \Delta y, z - \Delta z} \right)\Delta t + + \dddot a'\left( {t, x - \Delta x, y - \Delta y, z - \Delta z} \right)\frac{{\Delta {t^2}}}{2} \hfill \\ \end{gathered} $ | (13) |
式(13)中, ${\dddot a}$、${\dddot a'}$为三维上游点1阶、2阶变率, 上式可简记为:
| $ {P^{t + \Delta t}} = \dddot P + \dddot a\Delta t + \dddot a'\frac{{\Delta {t^2}}}{2} $ | (14) |
对(14)式, 因P的2阶变率${a'}$一般为未知, 若设Δt时段内$a' \equiv 0$, 即是设P的1阶变率a≡c, c为常数, 则得到"匀加速"显式预报方程:
| $ {P^{t + \Delta t}} = \dddot P + \dddot a\Delta t $ | (15) |
而若设Δt时段内2的2阶变率$a' \equiv c$, c为常数, 代入(14)式, 有:
| $ {P^{t + \Delta t}} = \dddot P + \dddot a\Delta t + c\frac{{\Delta {t^2}}}{2} $ | (16) |
对上式, 可代入P=a, 且考虑到P的2阶变率(a的1阶变率)为c, 有:
| $ {a^{t + \Delta t}} = \dddot a + \dddot a'\Delta t + \dddot a + c\Delta t $ | (17) |
(16) 式和(17)式联立, 求得$c = \frac{{{a^{t + \Delta t}} - \dddot a}}{{\Delta t}}$, 并回代(16)式, 则得到"变加速"隐式预报方程:
| $ {P^{t + \Delta t}} = \dddot P + \left( {{a^{t + \Delta t}} + \dddot a} \right)\frac{{\Delta t}}{2} $ | (18) |
上式${\dddot a}$和${{a^{t + \Delta t}}}$可理解为上游点起点变率和终点变率(18)式取二者平均值, 显然, 其计算精度将高于匀加速"显式预报方程(15)式。
上述预报方程表明:若拉格朗日气块不与外界发生任何物理交换(变率均为零), 则欧拉点预报值就等于上游点值。但是, 上游点一般都经过非线性路径, 而(11)-(12)式是气块在Δt时段内, 沿着"样条格式"路径, 带着全部物理属性, 并一路上受到各自变率作用, 到达欧拉预报点。
2 样条格式准拉格朗日平流 2.1 经纬网格-准均匀经纬网格全球样条模式采用球面Z (位势高度)坐标系。下面以球面1°×1°经纬网格"(A网格")作叙述, 更高水平分辨率可按比例推算。
1°×1°的A网格(0:360, 0:180)共有651 60个网格点。为采用周期三次样条做拟合, 在纬向取0°E/0°W为重合点, 即设定变量场在起始点'0'(0°E)值始终等于终止点'360'(0°W)值; 并且标量场(如p、T、q)及垂直矢量场(如w)在两极点始终赋予360个相同值, 而水平矢量场(如(u,v)、(au,av))始终赋予360个不同"三角函数"分解值(7)式。
在A网格基础上, 先设计一种准均匀经纬网格--B网格(表 1):B网格是从赤道向两极分段成倍递减A网格点, B网格保持纬向等距且B网格点与A网格点重合。由表 1可知, B网格减少了高纬带网格点, 使得网格点纬距相对于经距为"准均匀", 但B网格已不能直接做经向三次样条拟合。故实现准均匀经纬网格样条变换积分方案的核心思想是, 只做B网格点预报, 但做全部A网格点预报插值。对应于B网格, 存在如下的积分流程(以"静力平流"为例):
|
|
表 1 球面1°×1°经纬网格(A网格)和一种准均匀经纬网格(B网格) Table 1 The global 1°×1° latitude-longitude grid (A-grid) and the quasi-uniform latitude-longitude grid (B-grid):demote n as numbers of forecasting point in each degree of latitude and d as latitude distance (e.g., d=1, 1 degree of lantitude distance in the equator). |
① 在A网格上, 做变量场双三次曲面拟合[20], 实现球面标、矢量场二阶可导, 以对B网格点(包含极点)做水平平流预报。
② 在B网格上, 做水平平流变量和位移纬向三次样条拟合, 从而给全部A网格点赋予"预报"(水平平流和位移)插值。
③ 在A网格上, 做"水平平流位移"经向和纬向三次样条拟合, 求出样条格式水平散度场, 以对B网格点做平流增压和绝热增温预报, (并可做气块水汽相变及降水预报)。
④ 在B网格上, 做全部水平平流变量垂直三次样条拟合, 从而对B网格点做静力垂直平流预报。
⑤ 在B网格上, 再做全部"水平平流+垂直平流变量纬向三次样条拟合, 以给全部A网格点赋予"预报"插值。
上述积分流程关键的第①步骤是, 求"B网格上游点在A网格上水平坐标"。设某B网格点与同纬度最邻近A网格点相距Δx0, 则该上游点在A网格上的水平坐标为(x-Δx0-Δx,y-Δy)。
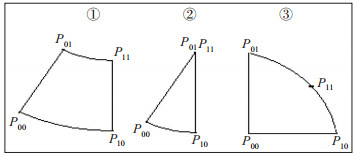
2.2 经纬网格与Hermite双三次曲面片图 1给出球面经纬网格(A网格)的3种拓扑矩形: ①一般形, ②临极点形和③极点形, 拓扑矩形4个角点均为变量场初值或预报值, 可按经纬方向, 设为P00、P10、P01、P11。
|
图 1 球面A网格上的3种拓扑矩形(①一般形, ②临极点形, ③极点形, P00、P10、P01、P11为变量场值) Fig. 1 Three topological rectangular figures of the spherical latitude-longitude grid (① General one, ② One adjacent pole, ③ One on the pole, and P00、P10、P01、P11 are variable field values). |
在A网格上容易实现各个变量场的Coons双三次曲面拟合[18-20], 与"拓扑矩形"A网格一一对应的正好就是Hermite双三次曲面片。上游点经过水平"双三次运动路径, 必将落在对应的A网格"二阶可导"变量场的某一片上。则在各个二阶可导变量场上, 既可迭代求得上游点在A网格上的水平坐标, 同时又求得上游点的全部预报变量值。
2.3 样条格式准拉格朗日平流方案设为无摩擦、无水汽、无辐散(不考虑散度场造成增压与绝热增温, 即设ap=aT≡0), 且不考虑垂直运动(即设w=aw=Δz≡0)、对于A网格上的单纯水平平流(即设au=av≡0), 容易按显式"匀加速"预报方程(15)式, 给出样条格式(12)式准拉格朗日法气压、气温、风场(水平平流)预报方程。因水平风为矢量场, 这里设欧拉点纬度为ϕ(-π/2 ≤ϕ≤π /2), 迭代求得上游点水平风速为(${{\ddot u}^t}, {{\ddot v}^t}$), 上游点到达欧拉点之后为(${u^{t + \Delta t}}, {v^{t + \Delta t}}$), 二者单位矢量纬向和经向弧度变化的"增量"为Δi和Δj (|Δi|﹤π/2和|Δj|﹤π/2), 则容易求得$\Delta j = \Delta y/{r_0}$和$\Delta i = \Delta x/\left[{{r_0}\cos \left({\phi + \Delta j} \right)} \right]$, 则有样条格式准拉格朗日平流(理想试验)预报方程:
| $ {P^{t + \Delta t}} = {{\ddot P}^t} $ | (19) |
| $ {T^{t + \Delta t}} = {{\ddot T}^t} $ | (20) |
| $ {q^{t + \Delta t}} = 0 $ | (21) |
| $ \begin{gathered} {u^{t + \Delta t}} = {{\ddot u}^t}\cos \Delta i - {{\ddot v}^t}\sin \Delta i;{v^{t + \Delta t}} = {{\ddot u}^t}\sin \Delta i - {{\ddot v}^t}\cos \Delta i \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {0 \leqslant \phi \leqslant \pi /2} \right) \hfill \\ \end{gathered} $ | (22) |
| $ \begin{gathered} {u^{t + \Delta t}} = {{\ddot u}^t}\cos \Delta i - {{\ddot v}^t}\sin \Delta i;{v^{t + \Delta t}} = {{\ddot u}^t}\sin \Delta i - {{\ddot v}^t}\cos \Delta i \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {\pi /2 \leqslant \phi \leqslant 0} \right) \hfill \\ \end{gathered} $ | (23) |
| $ {w^{t + \Delta t}} \equiv 0 $ | (24) |
本文二阶时空离散样条格式准拉格朗日(水平)平流理想场试验(预报方程(19)-(24)式), 采用上述球面拓扑矩形1°×1°经纬网格-准均匀经纬网格(A-B网格)。
3.1 平衡流试验平衡流试验是在A-B网格上, 通过双三次曲面变换, 插值求上游点水平运动路径及预报值, 检验其精确性及其程序正确性, 同时解决极区A网格点过密问题。
平衡流试验初值场设计为:q=v=w=0, 正压大气以等角速度围绕地球轴运动, 即有(设u0=20 m·s-1):
| $ u\left( {\lambda , \phi , z} \right) = {u_0}\cos \phi $ | (25) |
其水平运动满足准地转平衡:
| $ \frac{{dv}}{{dt}} = - RT\frac{{\delta \ln p}}{{\delta y}} - fu - \frac{{{u^2}\tan \phi }}{{{a_0}}} = 0 $ | (26) |
且满足静力平衡:
| $ \frac{{\delta \ln p}}{{\delta z}} = - \frac{g}{{RT}} $ | (27) |
全球模式大气均为定常气温直减率(设γ0=0.005 K·m-1):
| $ \frac{{\delta T}}{{\delta z}} = - {\gamma _0} $ | (28) |
将式(25)-(28)联立, 解得(设$G = \frac{{{\gamma _0}{u_0}}}{g}\left({2\Omega {a_0} + {u_0}} \right)$):
| $ T\left( {\lambda , \phi , z} \right) = {T_0} - {\gamma _0}z - \frac{G}{2}{\sin ^2}\phi $ | (29) |
| $ p\left( {\lambda , \phi , z} \right) = {p_0}{\left( {\frac{T}{{{T_0}}}} \right)^{\frac{g}{{r{\gamma _0}}}}} $ | (30) |
上面已设p0=1 020 hPa和T0=300.15 K, p0和T0分别为地面层赤道(ϕ=0)上的气压和气温。
将以上p、T、q、u、v、w初值场代入前述大气运动预报方程(19)-(24), 则不难求得干绝热、无摩擦、无辐散过程:$\frac{{dp}}{{dt}} = \frac{{dT}}{{dt}} = \frac{{dq}}{{dt}} = \frac{{du}}{{dt}} = \frac{{dv}}{{dt}} = \frac{{dw}}{{dt}} \equiv 0$, 故平衡流试验是正压大气作水平等角速度"永恒"运动试验。由理想场(25)、(29)、(30)式可知, 在任一位势高度上初值u、p、T场均为东西向平行"直线", 因"直线"流场上的路径与轨迹永远重合, 故模式时间积分(预报) u、p、T场将永远保持不变。
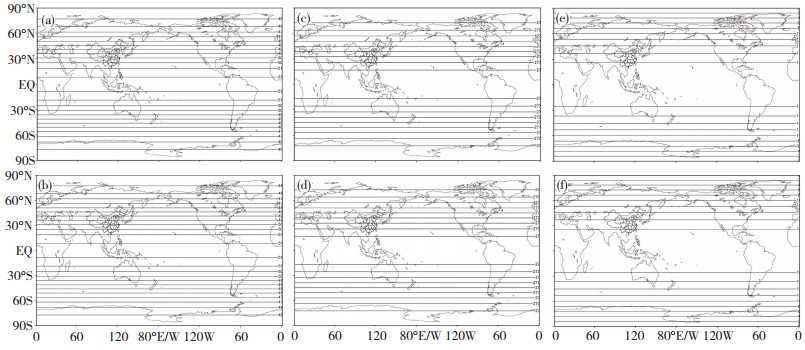
图 2给出"准地转"平衡流试验结果, 从中可见, 在全球1°×1°的A网格基础上, 在任一等高面(图 2为5749gpm)上, 从压、温、风初值场, 时间步长分别取300 s和600 s (图 2为600 s), 到30 d预报场, 都几乎不发生任何变化。该试验结果表明, 用非线性双三次曲面去拟合线性气压(质量)、气温(能量)和风(动量)场, 能够保证按线性流场求上游点水平路径与精确轨迹重合, 表现为大气质量场、能量场与动量场都在平行、均匀流动, 即采用双三次曲面拟合的"三次"平流兼容线性平流, 这种兼容性与谱展开在洋面上"存在虚假地形波"形成对照, 且试验从一个侧面证明了地转偏向力不做功。
|
图 2 平衡流试验(上图为初值分析场(5 749 gpm层), 下图为0 d预报场, (a)、(b)为气压(p, 单位:hPa)场, (c)、(d)为气温(T, 单位:K)场, (e)、(f)为风(u, 单位:m·s-1)场 Fig. 2 Exact test results of the balance flow with global "cubic model".The picture above are initial fields at the level of 5 749 gpm, The picture below are the same as "above", but for forecast fields in 30 d, (a) and (b) are pressure fields p (unit:hPa). (c) and (d) are temperature fields T (unit:K).(e) and (f) are wind fields u (unit:m·s-1). |
为验证在A-B网格(含极区、极点)上, 采用双三次曲面变换求准拉格朗日上游点路径的可行性、一致性、精确性与程序正确性, 同时借以解决极区网格点过密和极点奇异经典问题, 设计如下的二维(取地面层)过极地气流试验。
设为干(q=0)模式大气, 其平流满足地转平衡, 初值扰动气压场取为:
| $ p = {p_0}\exp \left( { - \frac{{2\Omega {a_0}{v_0}}}{{R{T_0}}}{{\sin }^3}\phi \cos \phi \sin \lambda } \right) $ | (31) |
式(31)中, p0=1 000 hPa, T0=300 K, v0=20 m·s-1, 则其水平地转风(u g,vg)为:
| $ \left( {{u_g},{v_g}} \right) = \frac{{R{T_0}}}{f}\left( { - \frac{{\delta \ln p}}{{{a_0}\delta \phi }},\frac{{\delta \ln p}}{{{a_0}\cos \delta \phi \lambda }}} \right) $ | (32) |
式(32)中, 地转偏向力$f = 2\Omega \sin \phi $, 则求得初值水平地转风为:
| $ \begin{gathered} {u_g} = {v_0}\left( {3{{\cos }^2}\phi - {{\sin }^2}\phi } \right)\sin \phi \sin \lambda ; \hfill \\ \;\;\;\;\;\;\;\;\;\;{v_g} = - {v_0}{\sin ^2}\phi \cos \lambda {\text{ }} \hfill \\ \end{gathered} $ | (33) |
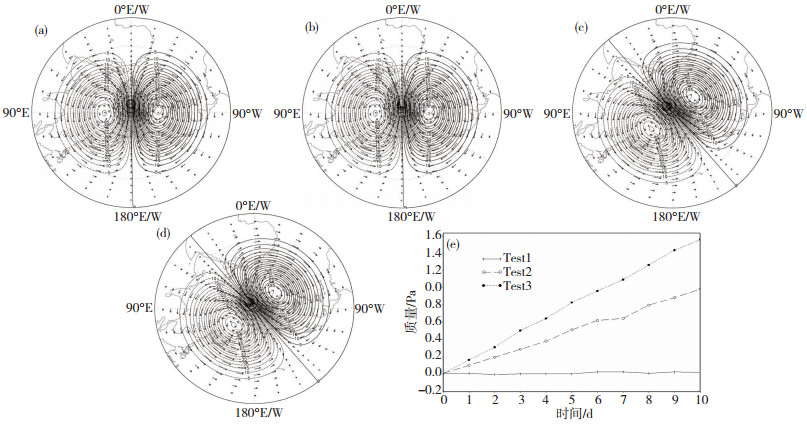
图 3给出过极地气流试验结果(北半球, 南半球图略), 从中可见, 其特征是北极点${\left({{u_g}} \right)_N} = 0, {\left({{v_g}} \right)_N} = - {v_0}$; 南极点${\left({{u_g}} \right)_S} = 0, {\left({{v_g}} \right)_S} = - {v_0}$(符合极点的水平风定义); 而在赤道${u_g} = {v_g} = 0$。
|
图 3 过极地气流试验结果地面气压扰动场(单位:hPa)和地转风场(单位:m·s-1)(a); 试验1(b)、试验2(c)、试验3(d)的10 d预报场; (e)试验1、试验2、试验3全球平均质量(单位:Pa)随时间变化, 纵坐标"0"表示全球平均质量初值为101 213.223 437 5 Pa Fig. 3 Exact test results of the cross-polar flow with global cubic model.(a) Perturbed pressure field (unit:hPa) and geostrophic wind field (m·s-1) at the surface layer.(b), (c) and (d) The same as "(a)", but for forecast in 10 d of Test 1, Test 2, Test 3, respectively.(e) The global mean masses change with time of Test 1, Test 2 and Test 3, and "0" of the ordinate indicates that the initial global mean mass be 101 213.223 437 5 Pa. |
由(32)式可知, 精确解地转风与扰动气压场等值线(梯度)始终保持平行(垂直), 则按流线求上游点路径应与精确轨迹重合, 则质量场不应发生任何变化。
实际在每一时间步积分之前, 都对各层的对数气压(ln p)场作球面双三次曲面拟合, 可近似求得水平地转风为(对比(32)式, 并参见图 3a):
| $ \begin{gathered} \left( {{u_g}, {v_g}} \right) \approx \frac{{R{T_0}}}{f}\left[ { - {{\left( {\ln p} \right)}^y}, {{\left( {\ln p} \right)}^x}} \right] \hfill \\ \left( { - \frac{\pi }{2} \leqslant \phi ﹤0和0﹤ \phi\leqslant \frac{\pi }{2}} \right) \hfill \\ {u_g} = {v_g} = 0\;\;\left( {\phi = 0} \right) \hfill \\ \end{gathered} $ | (34) |
且在每一时间步都做地面气压场的球面双三次曲面拟合之后, 容易求得全球(或半球)的大气质量及平均"气压"质量[20](平均气压=大气质量/球面积)。
一共设计3种水平分辨率均为1°×1°的过极地气流试验(表 2):
|
|
表 2 过极地气流试验设计 Table 2 The design of three exact tests of the cross-polar flow with global cubic model |
理论上, 试验1应始终保持地转风与等压线平行, 其扰动质量场不应随时间发生任何变化; 虽然试验2、3外加了一个纬向等角速度(5cosϕ), 在外加平流作用下, 它们的扰动质量场仅发生均匀转动, 也不应随时间发生变化。
分析可知,与初值场(图 3a)比较,试验1、2、3在积分10d后(图 3b-d), 全球(包括极区)都仍然保持很好的地转风与气压场关系, 且扰动质量场整体变形及质量变化均很小(图 3e)。试验1质量场几乎不随时间变化, 其预报10 d质量场变化比为1:0.999 999 923;同为300 s时间步长, 试验3预报10 d转动质量场变化比为1:1.000 015 438;试验2时间步长缩短为180 s, 其预报10 d转动质量场变化比为1:1.000 009 726(有收敛性); 且试验2、3均表现为质量场缓慢单调增加, 但三个试验总体形变及质量变化区别不大(三个试验之间因样条格式计算误差造成的差别几可忽略)。
3.3 Rossby-Haurwitz波试验Rossby-Haurwitz波(以下称"RH波")是线性正压涡度方程的近似解, 在一定假设条件下成为精确解。
假设地转偏向力($f = 2\Omega \sin \phi $)变化缓慢, 因着重对北半球作RH波试验, 故将$f$设在北纬45°, 即设$f = {f_0} = 2\Omega \sin \frac{\pi }{4}$, 则RH波试验精确解的位势高度扰动场h为:
| $ h\left( {\lambda , \phi , z} \right) = 2\Omega \sin \left( {\frac{\pi }{4}} \right)\frac{{\psi \left( {\lambda , \phi , z} \right)}}{g} $ | (35) |
式(35)中, ψ为无辐散风(uψ,vψ)的流函数场, 即有:
| $ \left( {{u_\psi }, {v_\psi }} \right) = \left( { - \frac{{\delta \psi }}{{{a_0}\delta \phi }}, \frac{{\delta \psi }}{{{a_0}\cos \delta \phi \lambda }}} \right) $ | (36) |
由式(36)可知, 精确解的无辐散风与流函数场等值线(梯度)始终保持平行(垂直), 同理, 按流线求上游点路径将与精确轨迹重合, 其质量场不应发生变化。
设h0(h0=300 gpm)为位势高度扰动场h的振幅, 且取u0=20 m·s-1, 又设$C = \frac{{g{h_0}}}{{{a_0}{f_0}}}$, 并给定"纬向4波流函数场ψ为:
| $ \psi = C{\cos ^2}\phi \cos \left( {4\lambda } \right) + {a_0}{u_0}\left( {1 - \sin \phi } \right) = \psi 1 + \psi 2 $ | (37) |
将(37)式代入(36)式, 求得,
| $ \begin{gathered} {u_\psi } = {u_{\psi 1}} + {u_{\psi 2}}, {u_{\psi 1}} = C\sin \left( {2\phi } \right)\cos \left( {4\lambda } \right) \hfill \\ {u_{\psi 2}} ={u_0}\cos \phi \;\;\;{v_\psi } = - 4C\cos \left( {2\phi } \right)\sin \left( {4\lambda } \right) \hfill \\ \end{gathered} $ | (38) |
式(38)中${u_{\psi 2}}$为纬向等角速度。
实际在每一时间步积分之前, 都对ψ作球面双三次曲面拟合, 可以求得其斜率ψx和ψy, 则有(对比(36)式):
| $ \left( {{u_\psi }, {v_\psi }} \right) \approx \left( { - {\psi ^y}, {\psi ^x}} \right) $ | (39) |
本文仅做静力正压大气二维(地面层) RH波试验。先对位势高度振幅h0, 做向等温大气气压振幅p0转换, 即将位势高度扰动场转换为气压扰动场(图 4a), 有(设${{\bar p}_0}$=840 hPa和${{\bar T}_0}$=273.15 K, ${{\bar p}_0}$和${{\bar T}_0}$分别为地面层北极点的气压和气温):
| $ {p_0} = {{\bar p}_0}\left[ {1 - \exp \left( { - \frac{{g{h_0}}}{{R{{\bar T}_0}}}} \right)} \right] $ | (40) |
这里, 一共设计6种RH波试验(表 3):
|
|
表 3 6种Rossby-Haurwitz波试验设计 Table 3 The design of six exact tests of the Rossby-Haurwitz waves with global cubic model. |
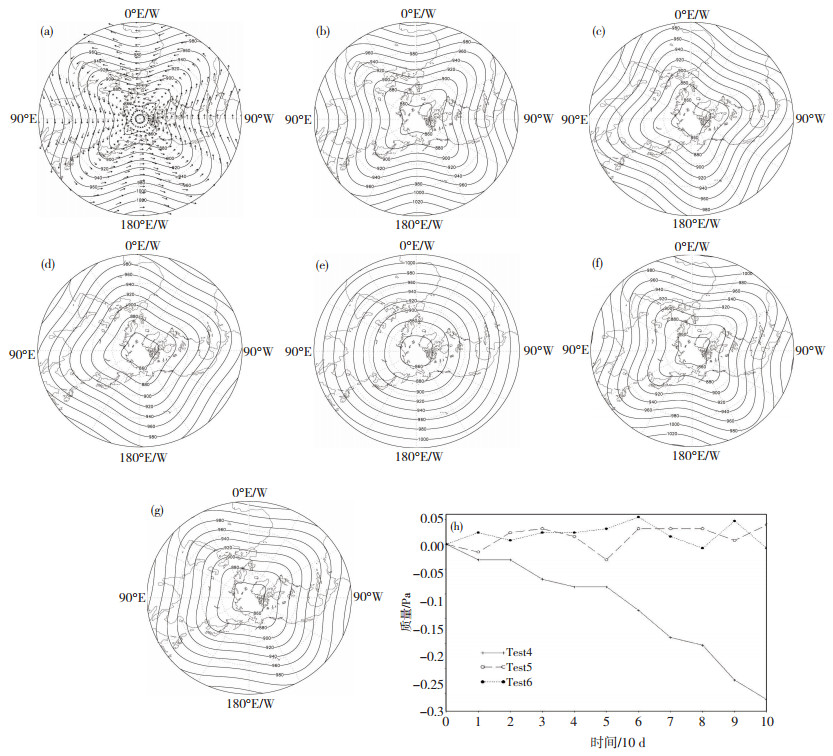
图 4给出RH波试验结果(北半球, 南半球图略), 从中可见, 试验4流场存在一"定常"纬向等角速度(${u_{\psi 2}} = {u_0}\cos \phi $, 图 4b), 而双三次曲面拟合可以保持原流场的球面对称性, 且求得的上游点路径与精确轨迹之间保持平行, 其预报的流函数(质量)场并无转动, 积分100 d扰动质量场变形及误差很小, 并且风场与流函数场始终保持无辐散风压场关系。
|
图 4 Rossby-Haurwitz波试验(分辨率1°×1°)结果海平面气压场和水平无辐散风分析场(a); 试验4(b)、试验5(c)、试验6 (d)的100 d预报场; 试验7(e)、试验8(f)、试验9(g)的300 d预报场; 试验4, 试验5, 试验6全球质量随时间变化(h), 纵坐标"0"表示全球平均质量初值为101 238.653 125 Pa, 横坐标单位为10 d Fig. 4 Exact test results of the Rossby-Haurwitz waves with global cubic model of 1°×1°. (a) Initial pressure and wind field at sea level.Forecast pressure field in 100 d of (b) Test 4, (c) Test 5, and (d) Test 6, and forecast pressure field in 300 d of (e) Test 4, (f) Test 5, and (g) Test 6.(h) Global mean masses change with time of Test 4, Test 5 and Test 6, and "0" of the ordinate indicates that the initial global mean mass be 101 238.653 125 Pa, while the abscissa is "10 days". |
试验5-9又都外加一个纬向等角速度(10cosϕ, 表 3), 对应于图 4c-g表明, 在外加平流作用下, 它们质量场都发生转动, 则试验5尽管时间步长(300 s)为试验4(600 s)的一半, 但其积分100 d"转动"质量场变形仍然比试验4"不转动"质量场变形要略大; 而同为"转动"的试验6时间步长(600 s)与"不转动"试验4相同, 但为试验5两倍, 同样积分100 d的质量场变形较试验5明显大、但较试验4更大, 其延长积分到300 d的试验7质量场已变得很"圆"了; 同为"转动"的试验8时间步长(60 s)仅是试验7的1/10, 其时间分辨率提高10倍, 相应计算量也增加10倍, 则其积分300 d质量场较试验7要"保真"多了。
另外, 试验9(图 4g)与试验8(图 4f)相比较, 尽管试验9水平分辨率提高了一倍, 其辨识度相应提高一倍(即其识别短波的能力提高一倍), 则其"平流"计算量增加4倍, 又其时间步长(120 s)为试验8的两倍, 其"时间积分"计算量相应减少一倍, 但其总计算量仍然是试验8的两倍, 而其保真度却差于试验8, 但已明显好于时间步长为600 s的试验7(图 4e)。
总之, RH波试验4、5、6(7和8)在积分100 d (300 d)之后, 均仍可以保持较好的无辐散风压场关系。它们预报气压场都有不同程度的"变形"误差, 但它们预报的总质量变化都非常缓慢(试验4、5、6, 图 4h)。时间步长600 s的试验4, 预报100 d"不转动"质量场变化比为1:0.999 996 913, 且质量变化呈单调减少; 时间步长300 s的试验5, 预报100 d"转动"质量场变化比为1:1.000 000 386;时间步长600 s的试验6, 预报100 d"转动"质量场变化比为1:0.999 999 923, 而其延长积分预报300 d (试验7)的"转动"质量场变化比同为1:0.999 999 923, 尽管试验7预报"转动"质量场变形程度要大得多(变圆了, 单调有界性); 而时间步长60 s的试验8, 其预报"转动"质量场较试验7要保真得多, 其预报300 d"转动"质量场变化比为1:1.000 000 540。
斯网格谱变换积分80 d的"偏圆"(关于极点不对称)结果[5], 形成鲜明对照。
4 理想场试验误差初步分析按大气动力学理论, 大气运动是一种准地转运动。平衡流试验描述的是"流线和迹线重合"的纯地转运动, 其流线和迹线均为平行于纬圈的"直线", 从极地投影看, 其为一个"圆"。因平衡流试验初始气压、气温和风场均为线性场, 而三次样条函数"兼容线性函数, 样条格式拟合压、温和风场的纬向斜率均恒为零, 既不存在三次样条拟合数学误差, 也不存在隐式迭代计算上游点路径(轨迹)误差, 上游点将匀速、惯性(无能量源汇)、永恒地流动, 从而使得压、温和风场都不随时间发生任何变化。
过极地气流试验和RH波试验, 其扰动气压场与风场, 一个是地转风压场关系, 一个是无辐散风压场关系, 它们非线性精确解的扰动气压场本来应是永远不变。但是, 过极地气流试验和RH波试验, 它们预报的扰动气压场随着时间积分都存在微小、缓慢的变化, 故从"时空连续"微积分精确解到"时空离散"样条变换近似解总存在误差, 误差直接来源有:①样条格式二阶空间余差; ②计算上游点路径误差。其中, 样条格式(其线性部分是二阶中央差)理论上将会带来预报大气波动的相速(传播)和群速(能量频散)误差。但上述两个试验表明, 样条格式描述波动相速与位相无误差, 只存在群速能量频散与振幅衰减误差, 而提高样条格式分辨率可以提高其辨识度, 相应提高时间分辨率, 还能够提高其保真度, 即是能够减少其预报波动能量频散及振幅衰减误差。
分析上述两个试验(图 3、图 4), 从初值场到预报场, 是本应永远不变的精确解扰动气压场, 因做经纬网格-准均匀经纬网格样条变换, 其对大气波动相速与位相描述正确, 但带来"虚假"群速能量频散与振幅衰减, 并且这种虚假振幅衰减与平流速度相关, 但虚假振幅衰减随时间步长减小而迅速放慢(样条格式"收敛性"), 从而证明, 减小预报误差最有效方法是提高模式时空分辨率。
至于上述两个试验全球总质量常呈现出微弱的单调增加", 这与扰动初值场和准均匀经纬网格样条变换都具备"球对称性"(关于极点和赤道对称)有关, 这里应指出, 地球转动和大气纯地转运动都具备球对称性, 故预报变量场随波动能量频散与振幅衰减而逐渐变"圆", 是由于准地转"频散"波动趋向于纯地转运动和样条格式带来振幅误差都具球对称性, 且两个试验均已证明, 准均匀经纬网格样条变换造成预报变量场"形变"及误差都具备球对称性, 同时, 这种形变"(变圆)及误差又是收敛、有界的, 对过极地气流试验和RH波试验其"形变"误差还可以是单调的, 其数学物理机制是, 样条格式带来虚假能量频散与振幅衰减"帮助"准地转波, 准地转波本身亦为频散波, 演变成为纯地转运动, 并且当变量场都变圆之后, 其将成为又一个平衡流试验, 而不再有质量、能量和动量变化。
5 结论和讨论(1) 与谱模式动力框架核心"高斯网格二维谱变换半隐式-半拉格朗日积分方案"相当, 本文研究样条模式动力框架核心"准均匀经纬网格双三次曲面变换显式-准拉格朗日积分(平流)方案":在经纬网格上, 对标量和矢量场(包括压、温、湿、风、广义牛顿力场)做双三次曲面拟合, 并仅对准均匀经纬网格点做准拉格朗日法平流预报--迭代插值求上游点水平路径与变量值, 同时, 做准均匀经纬网格各预报变量纬向三次样条, 以便对全部经纬网格点都赋予"预报值"。因样条变换二阶可导数学性质:收敛性、最优性、周期性、可光顺性等, 其比谱变换更加适合做全球统一(格点)数值模式, 理想试验证明, 经纬网格-准均匀经纬网格双三次曲面变换能够解决极区经纬网格点过密和极点奇异经典问题。
(2) 求准均匀经纬网格(含极点)上游点, 与欧拉法相比较, 准拉格朗日法样条格式"平流"包含"斜率"平流、"曲率"弯流和"挠率"扭流, 经理想试验, 验证了双三次曲面插值求上游点"三次运动"路径的可行性、(与其它格点模式)一致性和(二阶时空精度)精确性, 并证明了本文给出的北、南极点水平运动方程是正确的。
(3) 平衡流试验, 验证双三次曲面拟合"线性"压、温、风场, 能够保证上游点路径与轨迹重合, 表现为大气质量场和能量场在匀速、平行流动, 其压、温、风场保持不变, 表明三次样条函数兼容线性函数, 而谱不具备对线性函数兼容性。
(4) 过极地气流试验, 验证用双三次曲面拟合的地转风平流可以正确越过准均匀经纬网格极区与极点, 且能保持地转风压场关系, 其扰动气压场位相不发生变化, 而其振幅不发生明显变化, 若外加一纬向等角速度平流, 其质量场发生相应转动, 则其预报扰动气压场变形(误差)相应增快(增大), 但其总质量变化仍很小。
(5) RH波试验, 验证用双三次曲面拟合的无辐散风场与流函数场, 能够保持无辐散风压场关系, 其预报扰动气压场变形缓慢, 100 d预报质量场为单调缓慢减少, 若外加一纬向等角速度平流, 其质量场发生相应转动, 则其预报扰动气压场变形(误差)有所增快(增大), 但100-300 d预报总质量变化仍很小, 表明扰动气压场变形与质量变化可不成比例。
(6) 过极地气流试验和RH波试验表明, 预报误差来源于三次样条函数"二阶空间余差"的数学误差和上游点路径达不到精确轨迹的计算误差, 两个试验中因样条格式带来虚假波动振幅衰减及误差具备球对称性和收敛性, 且扰动质量场因虚假群速能量频散与振幅衰减而趋于"变圆", 这与准地转频散波趋向于纯地转运动相一致, 使得其质量变化为有界, 且对于过极地气流试验和RH波试验其"形变"误差还可以是单调的, 但样条格式能保持波动位相传播正确性, 理想试验还证明, 提高空间分辨率仅提高模式辨识度, 同时提高时间分辨率才能提高模式保真度, 故提高模式精度的最有效方法是同时提高模式时空分辨率。
| [1] |
周毅, 刘宇迪, 桂祁军, 等. 现代数值天气预报[M]. 北京: 气象出版社, 2002: 220.
|
| [2] |
Cote J, Gravel S, Methot A, et al. The operational CMC-MRB global environmental multiscale(GEM) model Part Ⅰ:Design considerations and formulation[J]. Mon Wea Rev, 1998, 126: 1373-1395. DOI:10.1175/1520-0493(1998)126 < 1373:TOCMGE > 2.0.CO; 2 |
| [3] |
Cote J, Gravel S, Methot A, et al. The operational CMC-MRB global environmental multiscale(GEM) model Part Ⅱ:Results[J]. Mon Wea Rev, 1998, 126: 1397-1448. DOI:10.1175/1520-0493(1998)126 < 1397:TOCMGE > 2.0.CO; 2 |
| [4] |
Bubnova R, Gello G, Bernard P, et al. Integration of the fully elastic equations cast in hydrostatic pressure terrain-following coordinate in the framework of the ARPEGE/ALADIN NWP system[J]. Mon Wea Rev, 1995, 123: 515-535. DOI:10.1175/1520-0493(1995)123 < 0515:IOTFEE > 2.0.CO; 2 |
| [5] |
薛纪善, 陈德辉. 数值预报系统GRAPES的科学设计与应用[M]. 北京: 科学出版社, 2008: 383.
|
| [6] |
Tanguay M, Robert A, Laprise R. A semi-implicit semi-Lagrangian fully compressible regional forecast model[J]. Mon Wea Rev, 1990, 118: 1970-1980. DOI:10.1175/1520-0493(1990)118 < 1970:ASISLF > 2.0.CO; 2 |
| [7] |
Ritche H, Beaudoin C. Approximation and sensitivity experiments with a baroclinic semi-Lagrangian spectral model[J]. Mon Wea Rev, 1994, 116: 1587-1598. |
| [8] |
Reich S. An explicit and conservative remapping strategy for semi-Lagrangian advection[J]. Atmospheric Science Letters, 2007, 8(2): 58-63. DOI:10.1002/(ISSN)1530-261X |
| [9] |
McDonald A, Bates J R. Semi-Lagrangian integration of a gridpoint shallow water model on the sphere[J]. Mon Weather Rev, 1989, 117: 130-137. DOI:10.1175/1520-0493(1989)117 < 0130:SLIOAG > 2.0.CO; 2 |
| [10] |
陈德辉, 胡志晋, 徐大海, 等. CAMS大气数值预报模式系统研究[M]. 北京: 气象出版社, 2004: 190.
|
| [11] |
HUANG Bo, CHEN Dehui, LI Xingliang, et al.Improvement of the Semi-Lagrangian Advection Scheme in the[9]GRAPES Model: Theoretical Analysis and Idealized Tests[J]. ADVANCES IN ATMOSPHERIC SCIENCES, 2014, 31(3): 693-704
|
| [12] |
奚梅成. 数值分析方法[M]. 合肥: 中国科学技术大学出版社, 1995: 377.
|
| [13] |
Fergusion J C. Multivariable curve interpolation[J]. J ACM, 1964, 2: 221-228. |
| [14] |
李建平. 计算机图形学原理教程[M]. 成都: 电子科技大学出版社, 1998: 328.
|
| [15] |
辜旭赞. "准拉格朗日法"和"欧拉法"数学一致性与三次插值函数算法时间积分方案[J]. 高原气象, 2010, 29(3): 655-661. |
| [16] |
吕美仲, 欧阳子济, 翟子航. 正压原始方程半隐式样条格式[J]. 气象科学, 1983(2): 1-11. |
| [17] |
Anita T L. Cubic spline collocation method for the shallow water equations on the sphere[J]. J Comput Phys, 2002, 179: 578-592. DOI:10.1006/jcph.2002.7075 |
| [18] |
辜旭赞, 张兵. 全球(Z)双三次数值模式的设计与个例模拟(Ⅰ)--模式动力框架设计[J]. 高原气象, 2008, 27(3): 474-480. |
| [19] |
辜旭赞, 张兵. 全球(Z)双三次数值模式的设计与个例模拟(Ⅱ)--个例模拟结果分析[J]. 高原气象, 2008, 27(3): 481-490. |
| [20] |
辜旭赞. 一种"准拉格朗日法"和"欧拉法"统一算法时间积分方案[J]. 气象学报, 2011, 69(3): 440-446. |
| [21] |
Polvani L M, Scott R K, Thomas S J. Numerically converged solutions of the global primitive equations for testing the dynamical core of atmospheric GCMs[J]. Mon Weather Rev, 2004, 130: 1384-1396. |
| [22] |
Xue M, Xu Q, Droegemeier K K. A theoretical and numerical study of density currents in non-constant shear flows[J]. J Atmos Sci, 1997, 54: 1998-2019. DOI:10.1175/1520-0469(1997)054 < 1998:ATANSO > 2.0.CO; 2 |
| [23] |
Held I H, Suarez M J. A proposal for the inter comparison of the dynamical cores of atmosphere general circulation models[J]. Bull Amer Meteror Soc, 1994, 13: 359-374. |
| [24] |
Williamson D L, Drake J B, Hack J J, et al. A standard test for numerical approximations to the shallow water equations in spherical geometry[J]. J Comput Phys, 1992, 102: 211-224. DOI:10.1016/S0021-9991(05)80016-6 |
| [25] |
Galewsky J, Richard K S, Polvani L M. An initial-value problem for testing numerical models of the global shallow-water equations[J]. Tellus, 2004, 56: 429-440. DOI:10.1111/tea.2004.56.issue-5 |
| [26] |
左瑞亭, 张铭, 张东凌, 等. 21层大气环流模式IAP AGCM-Ⅲ的设计及气候数值模拟Ⅰ:动力框架[J]. 大气科学, 2004, 28(5): 660-673. |
| [27] |
杨学胜, 陈嘉滨, 胡江林, 等. 全球非静力半隐式半拉格朗日模式及其极区离散处理[J]. 中国科学D辑:地球科学, 2007, 37(9): 1267-1272. |
| [28] |
杨学胜, 胡江林, 陈德辉, 等. 全球有限区数值预报模式动力框架的试验验证[J]. 科学通报, 2008, 53: 2418-2423. |
 2016, Vol. 35
2016, Vol. 35 
