2. 江西省大气探测中心,南昌 330046;
3. 南京信息工程大学江苏省农业气象重点实验室,南京 210044;
4. 江西省气象灾害应急预警中心,南昌 330046
2. Jiangxi Atmospheric Sounding Technology Centre, Nanchang 330046;
3. Jiangsu Key Lab of Agricultural Meteorology, University of Information Science and Technology, Nanjing 210044;
4. Meteorological Disaster Emergency Warning Centre of Jiangxi, Nanchang 330046
中国是受洪涝灾害影响最严重的国家之一,开展洪涝灾害风险评估对于加强灾害预警、规避洪涝风险具有重要作用。目前,气象灾害风险区划方法主要有基于指标的综合评估方法、基于数据的概率评估方法以及基于情景模拟的评估方法三种[1]。
基于指标的综合评估方法是相对采用较多的风险区划方法。Otar等[2]通过引入致灾因子和承灾体之间的关系模型,生成了格鲁吉亚地区的山洪风险区划图。赵霞等[3]选取地理高程、人口密度、人均GDP和历史灾情数据作为指标,采用快易的叠加分析法对研究区(内蒙古中部)进行了区域洪水灾害风险评价。蔡大鑫等[4]应用灾害风险形成的理论和方法,选取适合评价小流域暴雨洪涝灾害的敏感性、易损性和防灾减灾能力的空间指标,对流域的灾害风险进行了评价。随着GIS技术发展,国内外许多学者开始在指标综合评估基础上,借助GIS绘制相应的风险区划图并加以评述,从而提出相应的防御措施。如:盛绍学等[5]根据自然灾害风险评估基本原理,综合多种指标采用ARC⁃ GIS9.2的ModelBuilder建模工具,建立了暴雨洪涝灾害风险评估模型;马国斌等[6]基于自然灾害风险理论,借助GIS空间分析功能,采用归一化和层次分析法,对中国全国范围尺度进行了短时洪涝灾害危险性评估;Pandey[7]利用卫星遥感影像资料对印度比哈尔邦2008年洪涝面积进行评估,并将易涝区与社会经济数据相结合绘制出印度比哈尔邦地区暴雨洪涝风险图;缪启龙等[8]通过ArcGIS空间分析技术结合模糊综合评价法,编制了以100 m×100 m栅格为基本评价单元的杭州市暴雨洪涝灾害风险区划图;周峰等[9]将层次分析法(AHP)和次序权重平均法(OWA)相结合,构建了基于GIS的AHP-OWA洪涝灾害风险评价模型。
基于指标的综合评估方法,不能排除主观人为因素对指标构建的影响。因此,有人开始研究基于数据概率结合情景模拟的评估方法。如,李兰等[10]采用耿贝尔极值Ⅰ型分布法求取流域不同重现期面雨量,基于GIS的暴雨洪涝淹没模型计算不同重现期面雨量淹没范围和水深;运用灾害风险原理,制作漳河流域暴雨洪涝风险区划。而不同的降水时空分布,对洪水演进模拟甚至对防洪排涝工程的安全运行都会产生不同的影响[11]。前人研究中,对不同降水时空分布对洪水演进的影响少有提及,多采用“降水时间无变化,面雨量空间权重均一”的模拟方法[10]。因此,本文以模拟的淹没水深对研究区域开展基于不同降水情景下的暴雨洪涝致灾因子危险性评价,旨在说明降水时空分布对评价结果的影响。
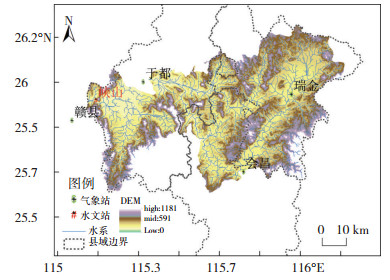
1 研究区域与数据来源本文选定的研究区域为贡水流域(图 1)。该流域位于江西省东南部,水系横跨瑞金市、于都县、会昌县三界,流域内人口约200万。峡山水文站位于赣县与于都的交界处,其控制面积约4 046 km2,警戒水位为109 m。流域内地势南高北低,且居民点多沿河道分布,河道下游地势平坦地区易受洪涝灾害影响。
|
图 1 江西省贡水流域基本信息 Fig. 1 Basic information schematic of Gong River Basin |
本文使用的资料或数据包括: (1)来源于江西省水文局的贡水峡山水文站2004年7月5—7日、2003年5月14—17日、2002年6月17—19和2001年6月12— 14日共计4次超警戒水位降水过程逐小时水位曲线变化图,以及该站1961—2004年逐日水文资料,选择同期35次超警戒水位降水过程作为致洪面雨量过程进行分析;(2)来源于赣县、于都、瑞金、会昌国家气象站1961—2004年逐小时降水资料,其中贡水流域面雨量采用克里金插值4站逐小时雨量获得;(3)来源于国家测绘局的水系、居民点、等高线等矢量数据和DEM数据,比例尺1:50 000,空间分辨率约25 m;(4)来源于Landsat TM卫星遥感解译数据的土地利用资料,分辨率约30 m;(5)来源于江西省灾情直报系统灾情数据库自1984年以来洪涝灾害历史灾情描述和记录。
2 致灾危险性评价将导致超警戒水位的降雨量作为诱发洪水的致灾因子,结合重现期雨量的计算[12],开展不同降水时空分布情景下的洪水演进模拟,以模拟淹没水深划分危险等级开展危险性评价。
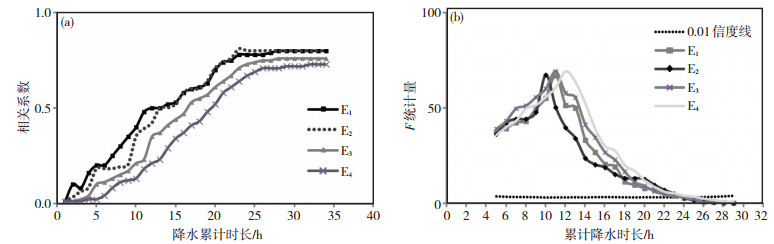
2.1 面雨量累积时长的确定计算面雨量必须明确前期降水对洪水水位上涨的影响,即确定前期累积降水量和洪水水位的相关性。利用峡山水文站2004年7月5—7日、2003年5月14—17日、2002年6月17—19和2001年6月12—14日共计4次洪水过程最高水位出现前的逐小时水位与对应时刻的逐小时滑动累积面雨量进行相关分析,并利用逐步邹氏断点检测法对两次过程的相关系数变化趋势进行分析[13]。其结果见图 2。
|
图 2 基于峡山水文站2004年7月5—7日(E1)、2003年5月14—17日(E2)、2002年6月17—19日(E3)和2001年6月12—14日(E4) 4次降水过程的洪水水位与前期降水时长的相关性(a)与累积降水时长相关系数的邹氏检验结果(b) Fig. 2 (a) Correlation of the flood levels and pre-precipitation duration and (b) F-statistic of correlation coefficient using Chow' s break point test based on the four rainfall events occurred in July 5 to 7 of 2004, May 14 to 17 of 2003, June 17 to 19 of 2002 and June 12 to 14 of 2001 at Xiashan hydrometric station. |
从图 2中可见,面雨量累积时长在23 h之后,邹氏断点检测F统计量通过置信区间为0.01的假设检验,4次洪水过程中从降水开始到累计时长23 h之后与水位的相关系数较高。这说明23 h之后相关系数变化趋于平稳。因此,将23 h的累积面雨量作为导致流域水位上涨的有效面雨量。
2.2 面雨量重现期的计算根据逐日水位资料,不能确定超警戒水位的水情具体发生在当日何时,其可能发生在该日00—23时(北京时,下同)任一时刻。因此,结合本文第2.1节的分析结果,采用以1961—2004年超警戒水位水情发生当日00时前推23 h作为开始时间、以超警戒水位水情发生当日23时作为结束时间共计47 h作为计算时长,由逐小时滑动计算47 h内最大23 h滑动累积面雨量,将每年最大的23 h累积面雨量作为重现期面雨量的计算样本。若某年无超警戒水位的降水过程,则选择以相同方法计算的该年最高水位降水过程的最大23 h滑动累积面雨量进行重现期计算序列的补充。
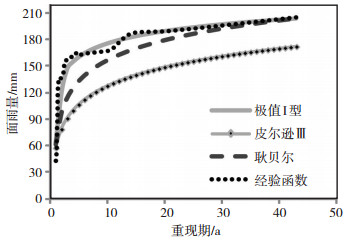
耿贝尔分布函数、极值Ⅰ型分布函数和皮尔逊Ⅲ型分布函数常被用来对水文、气象数据求重现期的极值分布函数[14]。本文选择这三种极值分布函数对样本序列进行拟合,利用其与序列的极值分布经验函数进行误差分析,选择最优拟合函数进行重现期面雨量计算[15]。表 1给出三种函数与极值函数经验分布的误差分析结果。由误差分析结果结合图 3发现,极值Ⅰ型分布与样本序列的极值函数经验分布最接近,拟合优度较高。再经最优参数估计分析,选择极值Ⅰ型分布函数结合最小二乘法的参数估计的最优方法对贡水流域降水序列5、10、20、50、100 a的重现期面雨量进行计算。
|
|
表 1 贡水流域降水极值分布函数误差分析 Table 1 Fitting-error using extreme value distribution function in Gong River Basin. |
|
图 3 使用耿贝尔分布函数、极值Ⅰ型分布函数和皮尔逊Ⅲ型分布函数拟合的贡水流域不同重现期面雨量(单位:mm)比较 Fig. 3 Comparison of area rainfall (unit: mm)with different return period in Gong River Basin fitted by three distribution functions such as Gumbel method, extreme-Ⅰ method and Pearson-Ⅲ method. |
采用极值Ⅰ型计算贡水流域超警戒水位的面雨量重现期,其结果如下(表 2):
|
|
表 2 基于极值Ⅰ型概率分布函数的贡水流域超警戒水位重现期面雨量 Table 2 Area rainfall with different return periods over alerting water level in Gong River Basin based on the extreme-Ⅰ probability distribution function. |
采用动态K均值聚类分析,将超警戒水位最大23 h面雨量的降雨历时除以总历时进行量纲一处理并作为横坐标,逐小时累积降雨量除以总降雨量进行量纲一处理并作为纵坐标,得到降雨过程的量纲一累积降雨曲线[16]。利用欧式距离公式,根据峰值雨量在降雨过程中出现的位置,按照最近距离准则将贡水流域35次降水过程分为7类,再根据雨量集中位置出现在降雨历时0%~40%处、40%~60%处、60%~100%处以及雨量均匀分布于整个降雨过程,将7类雨型主观合并为雨型Ⅰ—前期型降雨(以下简称雨型Ⅰ)、雨型Ⅱ—中期型降雨(以下简称雨型Ⅱ)、雨型Ⅲ—后期型降雨(以下简称雨型Ⅲ)和雨型Ⅳ—均匀型降雨(以下简称雨型Ⅳ)4类[17]。
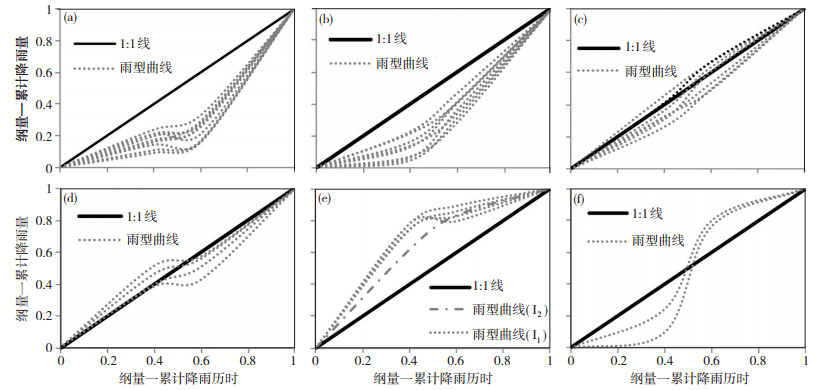
根据动态聚类分析结果,贡水流域超警戒水位最大23 h累积面雨量降水过程主要为雨型Ⅲ,共出现18次,出现概率约为51%。其中,雨型Ⅲ又可分为雨型Ⅲ(1)—后期集中型(以下简称雨型Ⅲ1)和雨型Ⅲ(2)—中后期集中型(以下简称雨型Ⅲ2)2种亚型(图 4a、b),这两种雨型各出现10次和8次,在所有降水过程中出现概率分别约为28%和20%。雨型Ⅲ 1在降雨历时40%~60%处的量纲一累积雨量趋势变化趋于平缓,而雨型Ⅲ2变化较陡。雨型Ⅳ降水出现11次,出现概率约为31%。雨型Ⅳ又可分为雨型Ⅳ(1)—均匀分布型(以下简称雨型Ⅳ1)和雨型Ⅳ(2)—前后期集中型(以下简称雨型Ⅳ2)2种亚型(图 4c、d),这两种雨型分别出现7次和4次,出现概率分别约为20%和12%。雨型Ⅳ1的累积雨量随时间变化趋于一条直线,而雨型Ⅳ2在降雨历时40%~ 60%处的量纲一累积雨量趋势较平缓。雨型Ⅰ降水共出现4次,其又可分为前期集中(简称雨型Ⅰ1)和前中期集中(简称雨型Ⅰ2)两种亚型(图 4e),这两亚型分别出现3次和1次。雨型Ⅱ出现次数最少,仅2次(图 4f)。
|
图 4 贡水流域各类雨型(a. Ⅲ1型;b. Ⅲ2型;c. Ⅳ1型;d. Ⅳ2型;e. Ⅰ型;f. Ⅱ型)聚类分析结果 Fig. 4 Dimensionless accumulative rainfall-duration curves in Gong River Basin for different rainfall patterns such as (a) type-Ⅲ1, (b) type-Ⅲ2, (c) type-Ⅳ1, (d) type-Ⅳ2, (e) type-Ⅰ and (f) type-Ⅱ by dynamic K-mean cluster analysis. |
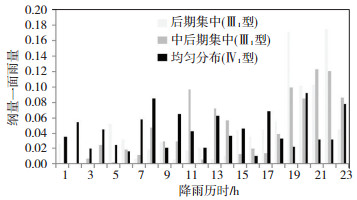
选择出现概率较高的雨型Ⅲ1、雨型Ⅲ2和雨型Ⅳ1,图 5给出属于这三种雨型的降水过程在23 h的量纲一面雨量的平均值,表 3给出出现次数最多的这三种雨型降水过程的发生时间、发生水位和23 h累积(面)雨量信息。
|
|
表 3 1961—2004年贡水流域雨型Ⅲ1、雨型Ⅲ2和雨型Ⅳ1的降水过程雨量和水位信息 Table 3 Rainfall and water level in Gong River Basin for type-Ⅲ1, type-Ⅲ2 and type-Ⅳ1 from 1961 to 2004. |
|
图 5 贡水流域雨型Ⅲ1、雨型Ⅲ2和雨型Ⅳ1在不同降水历时下的量纲一面雨量均值变化 Fig. 5 Mean change of dimensionless area rainfall for type-Ⅲ1, type-Ⅲ2 and type-Ⅳ1 in Gong River Basin in 23 hours. |
将贡水流域内超警戒水位降水过程中最大23 h累积面雨量出现时赣县、于都、瑞金、会昌4个国家气象站的小时雨量进行EOF分析[18],其结果见图 6。

|
图 6 1961—2004年贡水流域内超警戒水位降水过程中最大23 h累积面雨量出现时小时雨量前三个EOF模态(a. EOF-1;b. EOF-2;c. EOF-3)空间分布 Fig. 6 The first three EOF modes of hourly rainfall with the maximum cumulative rainfall in 23 hours of precipitation process when Gong River Basin' s water level is over the warning level from 1961 to 2004: (a) EOF-1, (b) EOF-2, and (c) EOF-3. |
从图 6中可见,第一模态(EOF-1)、第二模态(EOF-2)、第三模态(EOF-3)约占总量的90%,其中第一模态约为74%,第二模态约为10%,第三模态约为6%。第一模态显示,特征值向量范围在0.3~0.4之间,流域东部地区降水略多于流域西部,但全流域降水空间差异不大,近乎呈均匀分布态势。第二模态显示,向量特征值范围由北向南逐渐减小,流域降水相对集中在流域东北和西北部。第三模态显示,向量特征值范围分布极不均匀,流域降水主要集中在流域西部。
2.5 基于洪水模拟致灾因子危险性评价FloodArea模型以雨量输入、降水空间权重栅格和曼宁系数为输入数据,输出则为表示淹没水深的栅格数据[19-20]。将贡水流域超警戒水位降水过程小时雨量EOF分析结果中三种模态栅格数据均一化,再作为模型的降水空间分布权重栅格数据;由该流域各雨型的量纲一面雨量和重现期面雨量相乘,可计算出重现期雨量在23 h内的分布,并将其作为模型的雨量输入。
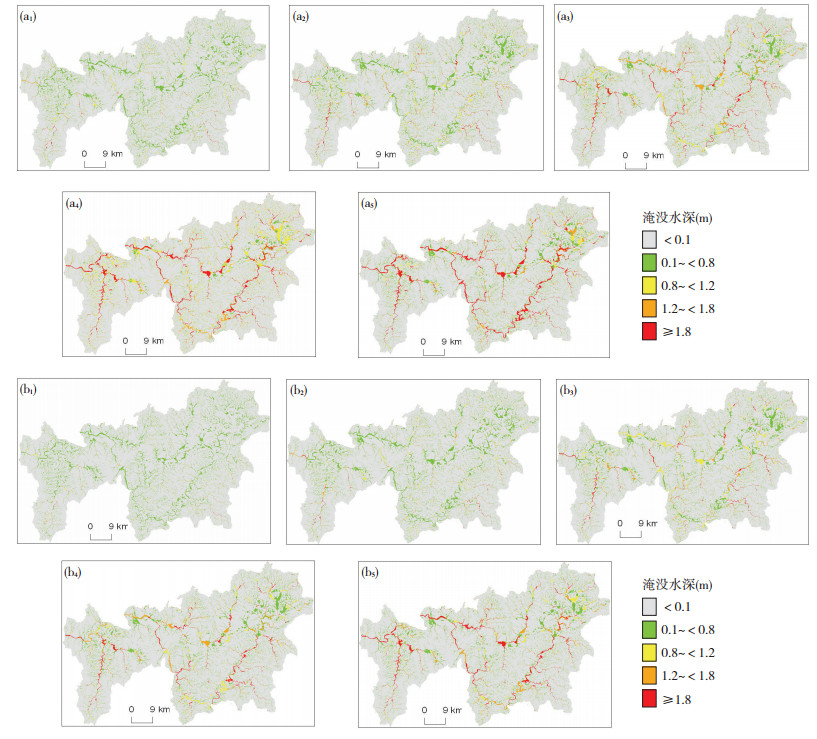
不同雨型结合不同面雨量空间分布模态可产生多种降水分布情景的组合。本文重点采用两种降水情景A、B驱动FloodArea模型进行洪涝演进模拟。情景A采用贡水流域降水空间分布第一模态结合雨型Ⅲ1的组合,情景B采用文献[10]中的“降水时间无变化,面雨量空间分布权重均一”的组合,以说明其与情景A的区别。同时,以流域内栅格的FloodArea模拟淹没水深(h, 单位: m)作为划分灾害危险等级的依据[21]。根据模型模拟结果结合实地调查的数据判断,将h≤ 0.1 m作为低危险性等级;考虑到洪水漫出堤防的水位,即0.1 m<h≤0.8 m设为次低危险性等级;考虑到洪水对农作物的危害,将0.8 m<h≤1.2 m设为中危险性等级;考虑到洪水对固定资产(如电视、冰箱等)的危害,将1.2 m<h≤1.8 m设为次高危险性等级;考虑到洪水危及到人的生命安全,将h>1.8 m设为高危险性等级,其模拟结果见图 7。
|
图 7 降水情景A和情景B下贡水流域5 a (a1, b1)、10 a (a2, b2)、30 a (a3, b3)、50 a (a4, b4)、100 a (a5, b5)一遇(面)雨量致灾危险性分布结果 Fig. 7 The Gong River Basin' s hazard risk map with (a1, b1) 5-year, (a2, b2) 10-year, (a3, b3) 30-year, (a4, b4) 50-year and (a5, b5) 100-year surface rainfall recurrence intervals under rainfall scenario A and rainfall scenario B. |
由模拟结果可知(图 7),该流域内沿河道附近较易出现致灾风险,两情景5 a一遇(面)雨量高、次高致灾区域约有5.3 km2和6.3 km2的面积差异(图 7a1、b1),其差异地区主要分布在该流域的西南部(即于都县西南部与赣县接壤区域)、东南部(即瑞金县东南部与会昌县接壤区域)和东北部(即瑞金县东北部和石城市接壤区域);两情景10 a一遇(面)雨量高、次高致灾区域约有13.0 km2和14.2 km2的面积差异(图 7a2、b2),主要差异地区分布在该流域的西南部、东南部和东北部;两情景30 a一遇(面)雨量高、次高致灾区域约有26.8 km2和29.6 km2的面积差异(图 7a3、b3),主要差异地区分布在该流域的中部地区(即于都县和瑞金县接壤地区);两情景50 a一遇(面)雨量高、次高致灾区域约有42.0 km2和8.9 km2的面积差异(图 7a4、b4),主要差异地区分布在该流域的东北部;两情景100 a一遇(面)雨量高、次高致灾区域约有47.2 km2和10.3 km2的面积差异(图 7a5、b5),差异地区主要在该流域的东北部和南部(即会昌县北部与瑞昌县接壤区域)。表 4给出不同情景模拟下的各风险等级的致灾面积。
|
|
表 4 降水情景A和情景B下贡水流域不同重现期(5、10、30、50、100 a)各风险等级致灾面积(单位: km2) Table 4 The Gong River Basin' s affected area (unit: km2) in different levels of risk with a rainfall recurrence period of 5 a, 10 a, 30 a, 50 a and 100 a under rainfall scenario A and rainfall scenario B. |
选择江西省灾情直报系统灾情数据库1984年以来贡水流域超警戒水位且面雨量超极值概率雨量的降水过程灾情实况描述进行验证。
1984年6月2日超警戒水位降水过程,符合动态K均值分类的后期集中型雨型,流域23 h累积面雨量超30 a一遇,灾情实况描述为“于都县贡水、梅江沿岸乡镇受灾,石城全县受灾”,基于情景A模拟出流域东北部发生高、次高风险区域要大于情景B,且宁都县境内该流域两岸基本呈现高、次高风险等级,比较而言,情景A与实况更为接近。
1994年6月16超警戒水位降水过程,符合动态K均值分类的后期集中型雨型,流域23 h累积面雨量超5 a一遇,实况描述为“于都县、赣县和石城全县受灾”,情景B作用下该流域内无高风险等级出现,而情景A在该流域西南部(即于都县西南部和赣县接壤区域)发生高、次高风险区域较多,较为接近实况灾情描述。
3 结论(1) 贡水流域超警戒水位降水过程中最大的23 h滑动累积降水量较适合采用极值Ⅰ型分布模型进行重现期计算;贡水流域超警戒水位降水过程的雨型主要呈现为雨型Ⅲ和雨型Ⅳ,其中出现最多的亚型分别为雨型Ⅲ1(后期集中)、雨型Ⅲ2(中后期集中)、雨型Ⅳ1(均匀分布)。4个国家气象站雨量数据EOF分析显示,贡水流域超警戒水位降水过程的面雨量分布主要呈现全流域均匀分布的态势,也会出现流域降水相对集中在流域东北和西北部而中南部降水较少以及西部降水集中而东西部降水分布极不均匀这两种情形。
(2) 以模拟淹没水深划分5个致灾危险性等级,在同一种降水情景的模拟结果显示,沿河道附近的致灾危险性等级明显高于流域内其他地方;随着重现期(面)雨量的增大,危险性等级逐步增高,出现灾害的可能性随之增加。
(3) 不同的降水情景会对洪涝致灾危险性区划结果产生不同影响。情景A与情景B的结果差异说明,均匀分布的雨型不是对所有降水过程的模拟都适用,采用情景A对后期降水集中的超警戒水位降水过程的区划结果与情景B相比更接近实况。因此,对研究区域开展基于洪水演进模拟的风险区划,应基于科学方法研究区域内降水时空分布规律,利用不同降水情景开展风险区划更为客观合理。
| [1] |
王春乙, 张继权, 霍治国, 等. 农业气象灾害风险评估研究进展与展望[J]. 气象学报, 2015, 73(1): 1-19. DOI:10.3969/j.issn.1005-0582.2015.01.001 |
| [2] |
Otar V, Nino T, Avtandil A, et al. Vulnerability, hazards and multiple risk assessment for Georgia[J]. Natural Hazards, 2012, 64(3): 2 021-2 056. DOI:10.1007/s11069-012-0374-3 |
| [3] |
赵霞, 王平, 龚亚丽, 等. 基于GIS的内蒙古中部区域洪水灾害风险评价[J]. 北京师范大学学报:自然科学版, 2007, 43(6): 666-669. |
| [4] |
蔡大鑫, 张京红, 刘少军. 海南岛万泉河流域暴雨洪涝灾害风险区划研究[J]. 中国农学通报, 2013, 29(23): 201-209. |
| [5] |
盛绍学, 石磊, 刘家福, 等. 沿淮湖泊洼地区域暴雨洪涝风险评估[J]. 地理研究, 2010, 3(29): 416-422. |
| [6] |
马国斌, 蒋卫国, 李京, 等. 中国短时洪涝灾害危险性评估与验证[J]. 地理研究, 2012, 1(31): 34-44. |
| [7] |
Pandey A C, Singh S K, Nathawat M S. Waterlogging and flood hazards vulnerability and risk assessment in Indo Gangetic plain[J]. Natural Hazards, 2010, 55(2): 273-289. DOI:10.1007/s11069-010-9525-6 |
| [8] |
缪启龙, 陈鑫, 俞布, 等. 杭州市暴雨洪涝灾害风险区划[J]. 长江流域资源与环境, 2012, 21(2): 163-168. |
| [9] |
周峰, 许有鹏, 石怡. 基于AHP-OWA方法的洪涝灾害风险区划研究——以秦淮河中下游地区为例[J]. 自然灾害学报, 2012, 21(6): 83-90. |
| [10] |
李兰, 周月华, 叶丽梅, 等. 基于GIS淹没模型的流域暴雨洪涝风险区划方法[J]. 气象, 2013, 39(1): 112-117. |
| [11] |
杨星, 朱大栋, 李朝方, 等. 按风险率模型分析的设计雨型[J]. 水利学报, 2013, 44(5): 542-548. DOI:10.3969/j.issn.0559-9350.2013.05.008 |
| [12] |
张正涛, 高超, 刘青, 等. 不同重现期下淮河流域暴雨洪涝灾害风险评价[J]. 地理研究, 2014, 33(7): 1 361-1 372. |
| [13] |
杨树成. 农村居民收入的政策效应检验[J]. 安徽农业科学, 2010, 38(22): 12 127-12 131. |
| [14] |
章国才. 气象灾害风险评估与区划方法[M]. 北京: 气象出版社, 2009: 127-128.
|
| [15] |
张子贤, 孙光东, 孙建印, 等. 城市暴雨强度公式拟合方法研究[J]. 水利学报, 2013, 44(11): 1 263-1 271. |
| [16] |
章基嘉, 孙照渤, 陈松军, 等. 应用K均值聚类法对东亚各自然天气季节500毫巴候平均环流的分型试验[J]. 气象学报, 1984, 42(3): 311-319. |
| [17] |
殷水清, 王杨, 谢云, 等. 中国降雨过程时程分型特征[J]. 水科学进展, 2014, 22(5): 617-624. |
| [18] |
何书樵, 郑有飞, 尹继福. 近50年长江中下游地区降水特征分析[J]. 生态环境学报, 2013, 22(7): 1 187-1 192. |
| [19] |
文明章, 林昕, 游立军, 等. 山洪灾害风险雨量评估方法研究[J]. 气象, 2013, 39(10): 1 325-1 330. |
| [20] |
姜智怀, 章毅之, 蔡哲, 等. 基于嵌入河道栅格的山洪灾害淹没模拟[J]. 气象, 2014, 40(8): 1 013-1 018. |
| [21] |
章国才. 暴雨洪涝预报与风险评估[M]. 北京: 气象出版社, 2012: 23-27.
|
 2016, Vol. 35
2016, Vol. 35 