模式水平分辨率提高可以从两个方面提高数值模式预报精度,一是减小数值计算误差,二是提高对更小尺度运动的分辨能力。当模式分辨率逐渐提高后,模式对于中小尺度降水特征的描述能力不断得到提升。数值模式降水预报性能的检验通常采用统计评分方法,如Threat Score(TS)和Equitable Threat Score (ETS), 但是当模式的分辨率逐渐提高以后,这类评分方法却不能很好地表达模式预报性能的提升。Tusti son等[1]和Gallus[2]指出,这类评分方法对水平分辨率具有依赖性,而且降水预报的水平分辨率越高,评分将受到更多的“惩罚”导致评分越低。也即,不同水平分辨率的预报是无法采用这类评分方法进行对比。研究指出[3~5],传统的检验方法由于采用“点对点”的比对,从而忽略了空间分布信息。比如高分辨率模式即使在降水强度和水平分布特征都有很准确的预报时,由于水平位置的差异可能会导致更多“空报”和“漏报”的“双重惩罚”(Double penalty),也会获得较低的评分。Weygandt等[6]针对IHOP试验期间的一个个例,通过将水平分辨率分别为10、12、20 km的预报降尺度到20、40、80 km分辨率进行评分的结果表明,ETS评分可以唯一地受到水平分辨率的影响,而且越低的分辨率对于评分越有利,因此不同分辨率预报的ETS评分没有可比性。Gilleland等[7]对多种检验方法进行了对比,重点对比了针对高分辨率降水的空间分布检验方法。同时,Gilleland等指出,可以简单地通过提高乖离率(Bias)来提高传统检验方法(如TS)的评分,也即高的空报率有利于高的TS评分。
中国区域模式分辨率正在不断提升,华北区域业务模式[8-10]分辨率2013年开始从9 km提高到3 km,国家气象中心和各区域中心的数值模式分辨率也在稳步提升, 因此有必要对模式的TS评分进行分析,从而客观评价模式的预报性能。中国各地的气象工作者对各模式、各区域的降水预报以及降水预报检验方法均进行了大量研究[11-20],得到很多降水检验方面的成果和结论,本文仅对数值模式的水平分辨率的改变对降水评分的影响进行初步探讨。
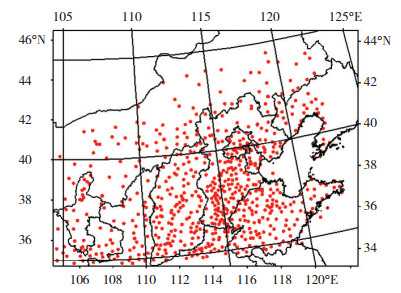
1 资料与方法采用华北区域业务模式(BJ-RUCv2.0)2013年4月1日—6月30日的3 km区域00UTC起始24 h预报的24 h累积降水,降水观测资料采用从国家信息中心提取的全国2 500站的加密观测24 h累积降水资料[11-12],其中参与华北区域检验的观测站数为649个,BJ-RUCv2.0模式区域以及参与评分的降水观测站点分布如图 1。
|
图 1 参与评分的站点分布图 Fig. 1 Stations used in the precipitation verification |
从参与评分的649个站点分布可看出,参与评分站点主要集中在华北东部和南部,内蒙区域内参与评分的站点相对较少。
首先将模式预报结果插值到水平分辨率0.03°的经纬网格(范围为104.48°—122.45°E、34.78°—44.5°N),根据数值预报中网格降水所代表的面雨量提法,升尺度方法采用线性滑动平均,分别采用平面3×3, 5×5, … 41×41点平均,可以认为得到0.09°、0.15°…1.23°分辨率的预报结果。
评分采用TS和BIAS评分,TS和BIAS评分公式如下:
| $ TS = {N_{\rm{a}}}/\left( {{N_{\rm{a}}} + {N_{\rm{b}}} + {N_{\rm{c}}}} \right) $ | (1) |
| $ BIAS = \left( {{N_{\rm{a}}} + {N_{\rm{b}}}} \right)/\left( {{N_{\rm{a}}} + {N_{\rm{c}}}} \right) $ | (2) |
其中:Na为实况有雨预报正确的站点数,Nb和Nc分别为空报和漏报的站点数。对于某一时段的总TS和BIAS评分,是根据累加后该时段的某降水量级的总Na、Nb、Nc,然后根据公式计算出评分。
文中不同级别降水强度选取的是通用阈值,即0.1 mm、10 mm、25 mm、50 mm、100 mm分别代表小雨、中雨、大雨、暴雨和特大暴雨阈值,具体计算TS和BIAS评分时,大于等于该阈值的降水均计入该阈值的评分。
2 降水TS评分对水平分辨率的敏感性 2.1 2013年5月26日降水评分分析研究期间尚不是华北雨季,因此降水的范围和强度还不大,2013年5月26日出现不同量级的降水并均有评分值,因而用当天00UTC起始的降水预报进行个例分析,看看升尺度后不同水平分辨率下各量级降水预报评分,讨论模式水平分辨率对降水预报评分的影响。
从BJ-RUCv2.0的模式预报和观测(图 2)对比来看,该次降水过程模式预报效果很好,无论降水区域还是强降水的分布,模式均提供了很好的预报。从插值到经纬网格后的降水分布以及5×5、9×9、…33×33个格点平均后的降水分布图(图 3)来看,原模式预报的降水区域细节很明显,而经过多格点平均后,参与平均的格点越多,小量级降水的区域越大,大量级降水特别是100 mm以上量级的降水区域越小,直至该量级的降水消失。

|
图 2 2013年5月26日BJ-RUCv2.0模式00UTC起始24 h预报的24 h累积降水量(a)和相应的观测值(b) Fig. 2 The 24 h accumulated precipitation valid from 00UTC May 26, 2013 for (a) forecasted by BJ-RUCv2.0 and (b) observation |

|
图 3 2013年5月26日00UTC起始BJ-RUCv2.0的24 h预报24 h累积降水插值到经纬网格后的分布(图标为1)、以及经过5×5、9×9、…33×33个格点平均后的降水分布图 (相应图标为5、9…33,色标同图 2中BJ-RUCv2.0模式预报) Fig. 3 The BJ-RUCv2.0 forecasted 24 h accumulated precipitation valid from 00UTC May 26, 2013, which has been interpolated to the lat-lon grid domain (symbol 1) and calculated by domain-average with 5×5, 9×9, …, 33×33 grids (corresponding symbols 5、9…33. Color code is the same as in Fig 2 BJ-RUCv2.0 forecast), respectively. |
从插值到649个观测站后各量级降水概率的分布(图 4)来看,随着参与平均的格点数增加,无雨的概率线性减小,小雨的概率线性增加,中雨的概率减小,大雨的概率有所增加,暴雨概率变化不明显,特大暴雨量级降水在平均格点达到9×9个后消失,可以看出模式分辨率的改变,对小雨以下量级的影响最大,对大量级降水的影响相对较小。

|
图 4 插值到参与检验的649个观测站点后各模式水平分辨率(横坐标为参与平均的单向格点数,1对应原模式,3对应3×3个格点平均,以此类推,图 5、7、8与此相同)和观测(对应obs)的各量级降水概率分布 Fig. 4 The precipitation probability of all model horizontal resolutions (abscissa is one-way grid points that involved average, 1 corresponding to original model, 3 corresponding to average of 3×3 grids, and so on. Same for Figs. 5, 7, and 8 below) and observation (corresponding obs) interpolated to 649 observations stations |
图 5为5月26日降水TS评分和BIAS评分,其中横坐标为原模式预报和参与平均的单向格点数,对应1为原模式预报,5为5×5个格点的平均,…41为41×41个格点的平均。纵坐标为评分的阈值,为了从图中更为准确地表现出模式水平分辨率对各阈值降水评分的影响,5月26日降水评分中,采用了0.1、1、3、5、10、15、20、25、30、50 mm共10个阈值,给出的均为大于等于该阈值的降水评分,特大暴雨量级降水的评分很低,且其随分辨率的变化趋势比较明显,这里就不再给出其评分。

|
图 5 原模式预报和多点平均的TS评分(a)和BIAS评分(b) Fig. 5 (a) TS and (b)BIAS scores of the original model and grid-averaged results |
从TS和BIAS评分来看,网格面平均对降水评分有很大影响,如0.1 mm阈值的降水TS评分从0.783提升到0.829,增加了0.046,1 mm阈值的降水TS评分从0.76增加到0.846,增加了0.086。从整体分布来看,1 mm、5 mm、20 mm和25 mm量级的降水TS评分随着水平分辨率的变粗呈增加趋势,3 mm和30 mm量级降水的TS评分随着分辨率变粗有所减小,0.1 mm、10 mm、15 mm和50 mm量级降水呈现中间高,两头低的分布趋势。从BIAS的评分来看,BIAS评分绝大部分小于1,说明整体以漏报为主,其中0.1~5 mm和20~30 mm量级降水的BIAS评分随分辨率的变粗呈上升趋势,但也只有0.1 mm和30 mm量级降水最后几个较粗分辨率的BIAS评分略大于1,30 mm量级的TS评分有所减小是因为空报增加而预报准确的站点数没有得到相应的增加所造成,10 mm量级的BIAS评分随分辨率变粗略有所减小,15 mm和50 mm量级降水的BIAS评分呈中间高、两头低的分布。整体来看,水平分辨率的改变对各量级降水的TS和BIAS评分均有比较明显的影响。
2.2 2013年4月1日—6月30日整个评分时段降水评分分析从整个评分时段的有无降水TS评分(图 6)来看,随着参与平均格点数的增加,TS评分整体增加,体现出有无降水的TS评分对模式水平分辨率比较敏感,数值模式水平分辨率的变化,会直接导致有无降水TS评分的改变。总体来看,有无降水的TS评分值主要落在0.5~0.6之间。

|
图 6 2013年4月1日—2013年6月30日00UTC起始24 h预报的24 h累积降水0.1 mm以上TS评分 (图标中的1表示原模式预报,11表示11×11个格点的平均,…) Fig. 6 TS score of the forecasted 24 h accumulated precipitation initiating from 00UTC during the period of April 1, 2013 to June 30, 2013 with the threshold of 0.1 mm (symbol 1 corresponding to original model, symbol 11 corresponding to average of 11×11 grids, …) |
从所有量级降水总TS评分(图 7)来看,0.1 mm量级降水评分随着参与平均的格点数呈线性上升的趋势,10 mm和50 mm量级的降水评分也有所增加;25 mm量级降水评分以13×13个格点平均的评分最高,呈现中间评分高,两边评分低的趋势;100 mm量级的降水量级TS评分有所减小,到参与平均的格点数达到9×9个以后,100 mm以上量级降水TS评分均为0。从整体TS评分来看,0.1、10、25、50 mm量级的降水总体来说有较强的参考价值,0.1 mm量级降水的TS评分在0.5~0.6之间,10 mm和50 mm量级降水TS评分在0.3~0.4之间,25 mm量级降水评分在0.2~0.3之间,特大暴雨量级的评分较低。

|
图 7 2013年4月1日—6月30日00UTC起始24 h预报的24 h累积降水的总TS评分(a)和BIAS评分(b) Fig. 7 (a)TS and (b)BIAS scores of the forecasted 24 h accumulated precipitation initiating from 00UTC during the period of April 1, 2013 to June 30, 2013 |
在降水场多网格点平均的基础上,如果平均后的降水量小于降水检验阈值,而平均前该格点降水量大于(或等于)降水检验阈值,则保留平均前该格点降水值,对保留大量级降水的新预报场进行检验,并给出与直接平均(评分见2.2节)的TS和BIAS评分相减后的评分差值。
从保留大量级降水减去直接平均后TS和BIAS评分差的分布(图 8)可看出,在多格点平均的基础上,保留原模式格点大于(或等于)检验量级降水在TS和BIAS评分上相对直接平均的评分有一定优势,对于0.1 mm量级的降水评分的影响最小,对于100 mm以上量级降水评分的影响最大,TS评分大部分比直接平均的高,只有50 mm量级在较少格点平均时,出现较多的空报而导致TS评分较低,其他量级降水的TS评分均较直接平均的高;BIAS评分均比直接平均的大,联系该时段直接平均的BIAS评分整体小于1,降水以漏报为主,这也从另一个侧面表明保留大量级降水后的预报效果较直接平均要好。

|
图 8 2013年4月1日—6月30日00UTC起始24 h预报24 h累积降水,保留大量级TS评分(a)和BIAS评分(b)减去直接平均之差 Fig. 8 The difference of the maximum (a)TS and (b)BIAS scores of the forecasted 24 h accumulated precipitation from their averages initiating from 00UTC during the period of April 1, 2013 to June 30, 2013 |
选取华北区域的测站密集区(110°—122.45°E;34.78°—41°N,见图 1),以0.03°、0.09°、0.15°…1.23°为分辨率画格,每个小格内参与检验的测站均不超过一个,具体做法是如果该网格内已经有一个测站,那么以后落在该网格内的测站就不再参与检验,每一个分辨率得到最后参与检验的测站数见图 9。固定参与检验的测站后,对模式预报进行多格点的滑动平均(见3.2节),给出检验的TS评分。

|
图 9 0.03°、0.09°、0.15°…1.23°网格分辨率下参与检验的测站数分布曲线 Fig. 9 The number of stations used in precipitation verification with 0.03°, 0.09°, 0.15°, …, 1.23° grid resolutions |
从参与检验的站点数来看,变化是很明显的,从0.03°分辨率时参与检验的测站数为481个,到1.23°分辨率时参与检验的测站数只有56个。从参与检验站点数的变化趋势来看,到0.21°分辨率时,参与检验的站点仅减少了29个,从481个变为452个,说明从现有降水观测的站点来看,在华北降水观测密集区域,能支撑的降水检验分辨率在0.2°左右。模式的高分辨率(如华北区域业务模式为3 km分辨率)和观测能支撑的检验分辨率之间存在的较大差异,会导致检验结果的可信度下降。
从小雨(0.1 mm)量级降水的TS评分随模式分辨率的变化趋势(图 10a)来看,无论测站的疏密度如何,TS评分均随着参与平均的模式格点数的增加而增加,可以看出模式分辨率的变化对小雨量级降水评分的影响非常显著;小雨量级的TS评分在测站疏密度为0.51°、0.87°和0.99°时,均出现了局部极大值,整体趋势来看,呈现中间TS评分高,两头低的分布形态。对于中雨(10 mm)量级降水的TS评分(图 10b),随着参与平均的格点数的增加,TS评分略有增加;测站疏密度对中雨量级降水的TS评分影响更加明显,在测站疏密度为1.11°左右时,评分达到极大值。对于大雨(25 mm)和暴雨(50 mm)量级降水的TS评分(图 10c和图 10d),随参与平均的格点数的变化趋势不明显,而随测站分辨率的变化存在显著的改变,大雨在测站分辨率为0.87°和1.11°左右时变化最显著,暴雨在测站分辨率为1.11°左右时变化最显著。整体来看,小雨量级降水的TS评分受模式水平分辨率的影响较大,中雨以上量级降水的TS评分受测站疏密度的影响较大。

|
图 10 2013年4月1日—2013年6月30日00UTC起始24 h预报的24 h累积降水的0.1 mm(a)、10 mm(b)、25 mm(c)和50 mm(d)量级的降水总TS评分随模式分辨率(纵坐标:坐标1对应原模式,5对应5×5个格点平均,…)和测站疏密度(横坐标:0.15对应0.15°×0.15°的网格内保留一个观测站,…)的分布 Fig. 10 The total TS score of 24 hours forecasted accumulated precipitation initiating from 00UTC during the period of April 1, 2013 to June 30, 2013 as a function of model resolution (ordinate: 1 corresponding original model, 5 corresponding average of 5×5 grids) and station density with thresholds (abscissa:0.15 corresponding to only keeping one observation station in 0.15°×0.15°grid, …) of (a) 0.1 mm, (b) 10 mm, (c) 25 mm and (d) 50 mm |
本文中测站疏密度的改变对于降水评分的影响,由于受参与评分的测站是随机选择而来的影响,其评分结果会存在一定的随机性,下一步会对参与检验的测站可能出现的各种情况进行研究,详细讨论测站的改变对模式降水评分的影响。
4 结论和讨论从各分辨率的TS评分来看,TS评分与模式的水平分辨率密切相关,随着参与平均的格点数增加,小雨量级的降水区域明显增加,TS评分稳步上升,对于中雨以上量级的降水,模式水平分辨率的改变对评分的影响趋势不明显。整体来说,TS评分与数值模式的水平分辨率有较强的关联,对不同量级的降水,影响的程度不一样。从改变同一区域参与检验测站疏密度来看,华北区域降水观测的密集区能支撑的降水检验分辨率在0.2°左右,测站的疏密度对各量级降水评分均有较大影响,特别是对大量级降水的TS评分影响更显著,测站的疏密度不同,评分的差距可能很大。
| [1] |
Tustision B, Harris D, Foufoula-Georgiou E. Scale issues in verification of precipitation forecasts[J]. J Geophys Res, 2001, 106(11): 775-778. |
| [2] |
Gallus W A. Impact of verification grid-box size on warm-season QPF skill measures[J]. Wea and Fore, 2002, 17: 296-302. |
| [3] |
Casati B, Coauthors. Forecast verification:Current status and future directions[J]. Meteor Appl, 2008, 15: 3-18. DOI:10.1002/(ISSN)1469-8080 |
| [4] |
Weygandt S S, Loughe A F, Benjamin S G, et al.Scalesensitivities in model precipitation skill scores during IHOP[C]. 22nd Conference Severe Local Storms. American Meteorological Society: Hyannis, MA, 4-8 October 2004
|
| [5] |
Jolliffe I T, Stephenson D B. Forecast Verification[M]//Wiley and Sons. A Practitioner's Guide in Atmospheric Science, 2003: 240
|
| [6] |
Wilks D S. Statistical Methods in the Atmospheric Sciences, 2nd edition[M]. Elsevier Academic Press, 2006: 627.
|
| [7] |
Gilleland E, Ahijevych D, Barvara G B. Intercomparison of Spatial Forecast Verification Methods[J]. Wea and Fore, 2009, 24: 416-430. |
| [8] |
范水勇, 陈敏, 仲跻芹, 等. 北京地区高分辨率快速循环同化预报系统性能检验和评估[J]. 暴雨灾害, 2009, 28(2): 119-125. DOI:10.3969/j.issn.1004-9045.2009.02.004 |
| [9] |
陈敏, 陈明轩, 范水勇. 雷达径向风观测在华北区域数值预报系统中的实时三维变分同化应用试验[J]. 气象学报, 2014, 72(4): 658-677. |
| [10] |
陈敏, 郑祚芳, 王迎春, 等. 2006年汛期北京地区中尺度数值业务降水预报检验[J]. 暴雨灾害, 2007, 26(2): 109-117. DOI:10.3969/j.issn.1004-9045.2007.02.003 |
| [11] |
王雨, 闫之辉. 降水检验方案变化对降水检验评估效果的影响分析[J]. 气象, 2007, 33(12): 53-61. |
| [12] |
王雨, 公颖, 陈法敬, 等. 区域业务模式6h降水预报检验方案比较[J]. 应用气象学报, 2013, 24(2): 171-178. DOI:10.3969/j.issn.1001-7313.2013.02.005 |
| [13] |
公颖. SAL定量降水预报检验方法的解释与应用[J]. 暴雨灾害, 2010, 29(2): 153-159. DOI:10.3969/j.issn.1004-9045.2010.02.009 |
| [14] |
张兵, 钟敏. GRAPES模式对湖北省汛期强降水预报的分类检验分析[J]. 暴雨灾害, 2009, 28(2): 137-142. DOI:10.3969/j.issn.1004-9045.2009.02.007 |
| [15] |
王叶红, 彭菊香, 公颖, 等. AREM-RUC 3h快速更新同化预报系统的建立与实时预报对比检验[J]. 暴雨灾害, 2011, 30(4): 296-304. DOI:10.3969/j.issn.1004-9045.2011.04.002 |
| [16] |
陈超君, 李俊, 王明欢. 2013年华中区域中尺度业务数值预报的客观检验[J]. 暴雨灾害, 2014, 33(2): 187-192. DOI:10.3969/j.issn.1004-9045.2014.02.012 |
| [17] |
刘凑华, 牛若芸. 基于目标的降水检验方法及应用[J]. 气象, 2013, 39(6): 681-690. |
| [18] |
胡胜, 罗聪, 黄晓梅, 等. 基于雷达外推和中尺度数值模式的定量降水预报的对比分析[J]. 气象, 2012, 38(3): 274-280. DOI:10.3969/j.issn.1001-7313.2012.03.003 |
| [19] |
熊秋芬. GRAPES_Meso模式的降水格点检验和站点检验分析[J]. 气象, 2011, 37(2): 185-193. DOI:10.3969/j.issn.1000-6362.2011.02.006 |
| [20] |
于晓晶, 于志翔, 辛渝, 等. 沙漠绿洲戈壁区域同化预报系统降水预报检验[J]. 暴雨灾害, 2014, 33(3): 281-289. DOI:10.3969/j.issn.1004-9045.2014.03.011 |
 2016, Vol. 35
2016, Vol. 35 