2. 中国舰船研究设计中心, 武汉 430064
2. China Ship Development and Design Center, Wuhan 430064, China
舰载机着舰时,若尾钩未能勾住阻拦索,则需要在触舰后加大推力并进行俯仰操纵,经过三轮滑跑、抬前轮和两轮滑跑等一系列飞行阶段后,最终安全地飞离航母舰面,这一过程称为逃逸复飞[1-2]。逃逸复飞关系到舰载机的着舰安全性:一方面,逃逸复飞任务是进场着舰规范规定的评估内容之一,可用于预估舰载机合适的进舰速度范围[3-4];另一方面,在开展机舰适配性研究时,也需要充分考虑着舰甲板风、航母运动等着舰环境特点[5],确定满足逃逸复飞安全要求的作战使用条件,如航母航速要求、着舰海况等级限制等。
国外主要通过飞行员在环的地面模拟仿真试验和飞行试验的方法,来评估舰载机的逃逸复飞特性和飞行品质。目前可查阅到的公开文献十分有限,且未给出具体的安全性评定指标[2]。国内的研究主要是通过运动建模与仿真计算分析舰载机的逃逸复飞特性[6-9],分别讨论了甲板运动、舰面气流扰动、螺旋桨动力等因素对舰载机逃逸复飞特性的影响[10-11]。然而,目前较少见有针对逃逸复飞任务中机舰总体参数适配关系的研究。
在本文中,首先,针对逃逸复飞的任务要求,提出了离舰滑跑距离、逃逸复飞段最大迎角相对进舰配平迎角的增量(下文简称迎角增量)和着舰时的俯仰角3个安全性评定参数,用于研究和分析舰载机的逃逸复飞特性。其次,建立了数字飞行员模型用于开展数字虚拟飞行仿真计算,从而可以更准确地完成舰载机逃逸复飞的全过程数学仿真。在此基础上,计算分析了舰载机在不同着舰重量、进舰速度下的逃逸复飞特性,并获得了满足逃逸复飞安全要求的参数适配包线。最后,定量分析了舰载机重心位置、航母航速、不同海况等级等对参数适配包线的影响。研究结果可以为舰载机总体方案设计、机舰适配性研究、作战使用条件的确定等提供参考。
1 逃逸复飞的安全性评定参数美军联合军种规范指南(JSSG—2001A)的附录D给出了舰载机逃逸复飞任务的明确定义,并简述了逃逸复飞的飞行任务与操纵策略[1]。此外,国军标GJB 2753—96中也规定了舰载机着舰载荷的具体要求[12],对于保证逃逸复飞时飞机起落架的结构强度安全具有指导意义。因此,本文基于上述文献,提出以下3个参数,用于评定舰载机逃逸复飞的安全性。
1) 舰载机从三轮着舰到逃逸复飞拉起这一过程的离舰滑跑距离(Xbo,见图 1),是JSSG—2001A[1]明确指出可以表明舰载机逃逸复飞性能的一项参数,其能够反映飞机短距起飞的滑跑特性,以及机舰同向运动时相互位置变化的情况。逃逸复飞过程与正常舰面起飞不同,由于在此期间飞行员需进行一定的拉杆操纵,当飞机在到达甲板末端前就离舰爬升,不出现航迹下沉才是理想的逃逸复飞[3]。由此可知,通过计算使飞机到达甲板末端前就离舰爬升的逃逸复飞的滑跑距离,并与航母所能提供的甲板跑道长度进行比较,就能够判断逃逸复飞是否安全。
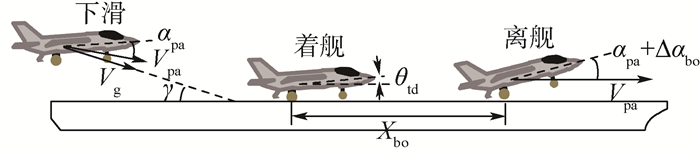
|
| 图 1 逃逸复飞过程及安全性评定参数示意 Fig. 1 Illustration of bolter process and its safety evaluation parameters |
2) JSSG—2001A[1]指出舰载机在逃逸复飞过程中,其迎角应保持在αpa和αpa+3°之间(αpa为进舰配平迎角),且升力系数CL不大于0.9CLmax。因此,本文提出逃逸复飞段最大迎角相对进舰配平迎角的增量(Δαbo,见图 1)这一参数作为安全性评定参数,并且要求迎角增量不大于3°,原因如下:①舰载机在进舰下滑到逃逸复飞的全过程中,均处于低速大迎角飞行状态,此时既要保证飞机以足够大的迎角飞行,也要保证其在逃逸复飞段不出现因迎角过大而失速的危险,因此采用迎角增量这一参数对飞机的飞行迎角进行约束,从而保证其在合理、安全的范围内变化;②迎角过大还可能诱发飞机的横航向运动与操纵效能下降等问题,在逃逸复飞段会给飞行员的操纵造成不利影响;③在舰载机下滑变轨机动任务的规范要求中[1],也对飞机迎角增量提出了类似的准则要求,即迎角增量不超过失速迎角与机动初始迎角两者之差的50%。
3) 基于飞机纵向地面操稳特性的要求,本文提出采用飞机着舰时的俯仰角(θtd,见图 1)作为逃逸复飞安全性的评定参数,其原因在于:如果着舰时的俯仰角过小,飞机就可能出现着舰回跳、前起落架结构损坏等险情,因此需要限制飞机着舰时的俯仰角大小。本文确定θtd的设计要求时,主要考虑了飞机的停机角和航母甲板运动的纵摇角,并且还预留了0.5°作为安全裕度。
图 1表征了舰载机的逃逸复飞过程,并且简要地示意了一些主要的物理参数量,其中,Vpa为飞机进舰空速,Vg为飞机进舰地速,γ为飞机航迹倾角。
2 逃逸复飞的参数适配包线逃逸复飞是典型的高风险试飞科目,飞行员需要具有较丰富的飞行经验和较高的操纵技术才能完成这一科目。本文采用数字虚拟飞行仿真计算的方法,从而较准确地分析了舰载机的逃逸复飞特性,并且计算相应的参数适配包线。
2.1 数字虚拟飞行仿真计算模型数字虚拟飞行仿真计算方法[13]是指在设计阶段,由工程技术人员对飞机飞行动力学和飞行员操纵行为进行数学建模,并利用数字计算机对选定的考核飞行任务开展人机闭环仿真计算,依据所得结果考察飞机飞行和运营的安全性是否能够满足设计的要求。数字虚拟飞行仿真计算模型的完整结构如图 2所示。
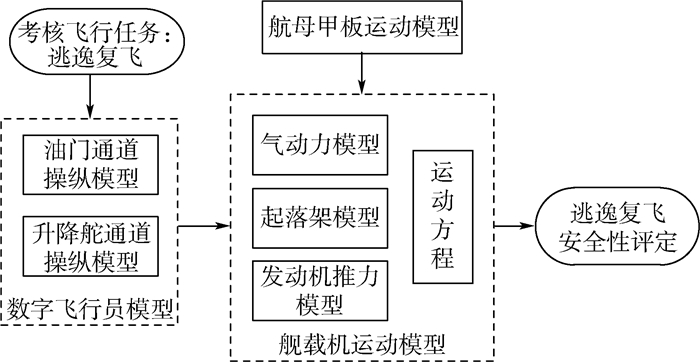
|
| 图 2 数字虚拟飞行仿真计算模型结构 Fig. 2 Structure of digital virtual flight simulation model |
1) 舰载机运动模型
飞机的6自由度动力学方程如下:
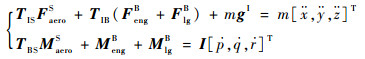
|
(1) |
式中:F和M分别为力和力矩向量,其上标表示该力或力矩投影到某一坐标系下的分量(S、B分别指稳定轴系、机体轴系),其下标aero、eng、lg分别指气动力、推力、起落架作用力;TIS、TIB、TBS为各个坐标系间的转换矩阵;m为飞机的着舰重量;I为飞机的转动惯量矩阵;g为重力加速度向量,上标I表示惯性参考系;x、y、z分别为飞机重心的3个坐标位置;p、q、r分别为飞机的3轴角速度。
通过建立起落架模型,可以计算前起与主起对于机体的作用力和力矩,从而准确地反映舰载机在触舰、三轮滑跑、抬前轮等一系列逃逸复飞过程中的动态响应特性。起落架支柱的缓冲力一般分为空气弹簧力和油液阻尼力,可由支柱压缩量及其变化率计算获得[14]。
舰载机的油门与升降舵作动器的动力学模型采用一阶环节表示,其相应的时间常数分别为0.7 s和0.12 s。
2) 数字飞行员模型
数字飞行员模型是指模拟飞行员在逃逸复飞任务中的操纵行为,并给出操纵指令的数学模型,包括油门与升降舵2个通道,从而完成人机闭环数学仿真。
油门通道的操纵模型如式(2)所示。在飞机触舰前,油门指令δpc保持下滑配平时的指令δp, trim不变;在飞机触舰后,需要考虑飞行员的反应时间延迟,一般取为0.5 s,在此期间油门指令仍然不变;在此之后,飞行员将给出最大油门指令δp, max,从而加大发动机推力进行逃逸复飞。ttd为飞机触舰时刻。
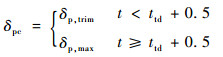
|
(2) |
升降舵通道的操纵模型描述如下:在飞机触舰前,升降舵指令保持下滑配平时的指令不变;在飞机触舰后,飞行员的操纵反应时间延迟约为1 s,在此期间升降舵指令同样不变;在此之后,要求飞行员通过操纵使飞机保持较为理想的离舰爬升迎角。对于技术较为熟练的飞行员,这一迎角误差补偿任务可以采用McRuer模型进行描述[15]:
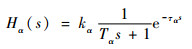
|
(3) |
式中:kα为飞行员对迎角误差的操纵增益;Tα为飞行员滞后补偿时间常数;τα为飞行员的信息反应延迟时间;s为复变量。
此外,在操纵模型中还需要加入俯仰角速度反馈,从而表征飞行员对角速度的感受和操纵[16-17]。图 3给出了完整的升降舵通道飞行员操纵模型。图中:Hq(s)为俯仰角速度感受回路;Hnm(s)为人体肌肉动作延迟模型,可用频率为9 rad/s、阻尼比为0.7的二阶环节描述;αerr为迎角误差;δec为升降舵指令。
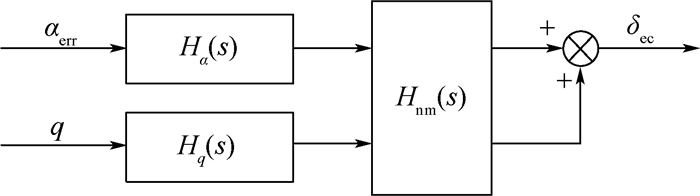
|
| 图 3 升降舵通道的飞行员操纵模型 Fig. 3 Control model of pilot in elevator channel |
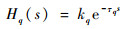
|
(4) |
式中:kq为飞行员的运动感官增益;τq为飞行员运动神经的延迟时间。
3) 航母甲板运动模型
航母的甲板运动较为复杂,既与航母自身的特征长度、排水量、航速航向等相关,也受到海浪和海面风等海况条件的影响,往往难以获得准确的解析模型,因此在工程研究时,多采用频谱模型或正弦模型加以描述[18]。本文采用简化和统一的正弦模型[19]对航母的甲板运动进行建模,如式(5)所示,主要考虑了垂荡、纵摇、横摇等3个运动,不同海况下的建模数据如表 1所示。通过随机设置模型的初始相位,可以获得多组不同航母甲板运动的时域仿真曲线。
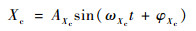
|
(5) |
| 参数 | 4级海况 | 6级海况 |
| 垂荡位移幅值/m | 0.68 | 1.63 |
| 横摇角幅值/(°) | 0.62 | 1.45 |
| 纵摇角幅值/(°) | 0.52 | 1.24 |
| 垂荡频率/(rad·s-1) | 0.35 | 0.35 |
| 横摇频率/(rad·s-1) | 0.29 | 0.29 |
| 纵摇频率/(rad·s-1) | 0.52 | 0.52 |
式中:Xc指航母的垂荡位移Δzc、纵摇角θc和横摇角ϕc,单位分别为m、(°)和(°);A为甲板运动的幅值,单位为m或(°);ω和φ分别为甲板运动的频率和初始相位,单位分别为rad/s、rad。
2.2 仿真算例采用某舰载机的总体与气动数据来建立本文算例飞机的运动模型。飞机的典型着舰重量约为10×103 kg,机翼面积约为55 m,翼展约为14 m,弦长约为5.4 m,单发最大推力约为50 kN,进舰下滑时的航迹倾角为-3.5°。算例航母参考“尼米兹”级航母进行运动建模[19],其斜角甲板跑道长度约为235 m,典型航速约为20 kn。
根据算例飞机与航母的有关参数,确定逃逸复飞的安全准则如下:按航母最后一根阻拦索到斜角甲板末端的跑道长度,取Xbo<155 m;基于JSSG—2001A[1]中的要求,取Δαbo<3°;飞机的停机角约为2°,航母的最大纵摇角约为1.5°,再加上0.5°作为安全裕度后,取θtd>4°。
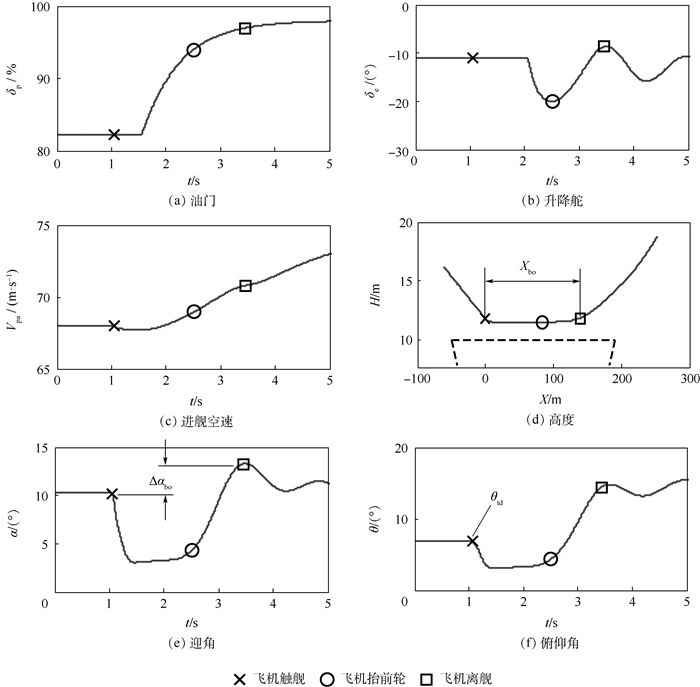
图 4给出了一组逃逸复飞的仿真计算结果。此外,离舰滑跑距离、迎角增量、着舰时的俯仰角等3个安全性评定参数也在对应的仿真曲线中作出了标识。
|
| 图 4 逃逸复飞的仿真算例 Fig. 4 A simulation sample of bolter |
根据图 4可知:
1) 仿真计算开始时,舰载机位于舰尾上方,净空高度约为4.7 m,在飞机触舰前飞行员保持油门和升降舵位于初始的配平下滑状态。仿真计算1 s时舰载机触舰,通常情况下飞行员做出逃逸复飞的决策判断时间约为0.5~1 s,因此飞行员在1.5 s左右给出了油门操纵指令,在2 s左右给出了升降舵操纵指令。由于发动机推力变化的时间延迟,故直至第4 s时发动机才达到最大推力状态。开始滑跑后,飞机的迎角和俯仰角均减小,因此飞行员首先给出纵向拉杆操纵指令。飞机抬前轮后开始两轮滑跑,迎角和俯仰角有所增大,此时飞行员为使飞机具有适当的飞离姿态,减小了升降舵的拉杆量,从而避免飞机过快抬头,如图 4(f)所示。
2) 舰载机着舰时的俯仰角约为6.8°,因此不会出现前起落架先触舰的情况;迎角增量约为2.9°;飞机的离舰滑跑距离约为139 m,故飞机能够在到达甲板末端前飞离舰面开始爬升。因此,本次逃逸复飞是安全的。
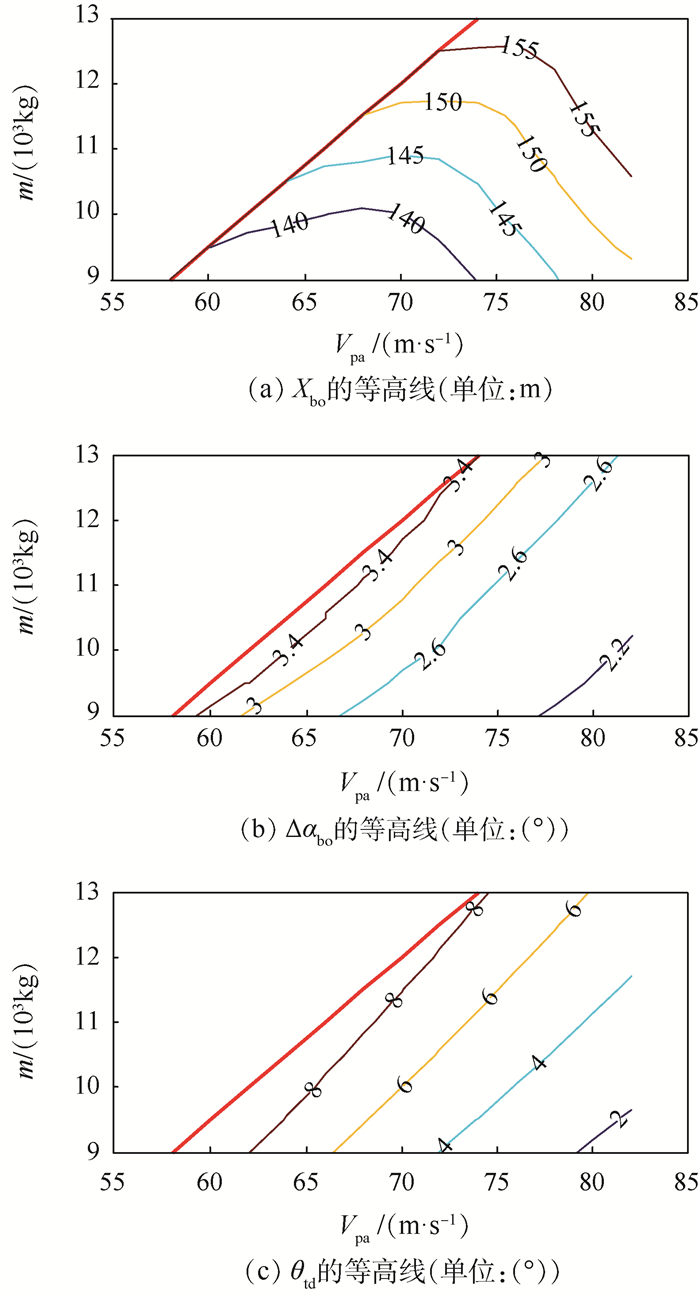
2.3 评定参数的变化规律以进舰速度为横坐标,着舰重量为纵坐标,重复2.1节的数字虚拟飞行仿真计算,可以获得舰载机不同着舰重量和进舰速度下的逃逸复飞性能,并以图 5所示的等高线形式进行描述。图 5能够简洁、直观地表示着舰重量、进舰速度对于舰载机逃逸复飞特性的影响,从而为确定合适的设计着舰重量、进舰速度提供参考。
|
| 图 5 不同着舰重量和进舰速度下的逃逸复飞性能 Fig. 5 Bolter performance with different landing weights and approach velocities |
分析图 5可知:
1) 在所有的等高线图中,其左侧直线段为下滑配平约束限制,即在该线段以左、以上的着舰重量、进舰速度组合下,舰载机无法建立稳定的下滑着舰飞行状态,因而也无法进一步分析其逃逸复飞特性。
2) 舰载机的着舰重量增大,则其在逃逸复飞时的离舰滑跑距离就随之增加。而在同一着舰重量下,离舰滑跑距离将随进舰速度的增加呈现出先减小后增大的特点,其原因在于:①增大进舰速度能够使舰载机更快地获得爬升拉起所需的升力,从而完成逃逸复飞并离舰,因此离舰滑跑距离有所缩短;②由于飞行员需要一定的反应和决策时间才能给出逃逸复飞操纵指令,因此在相同的滑跑时间内,离舰滑跑距离将随机舰相对速度增大而相应增加。
进一步,根据图 5(a)所示的仿真结果还可以看出:当着舰重量为10×103 kg时,较为理想的进舰速度约为66~70 m/s,此时的离舰滑跑距离最短,约为140 m。而当着舰重量为12.5×103 kg时,最短的离舰滑跑距离为155 m,对应的进舰速度范围为73~77 m/s。由此也就表明,在每一着舰重量下,均对应存在一个最佳的进舰速度范围,从而能够使逃逸复飞的离舰滑跑距离最短。
3) 如图 5(b)所示,迎角增量的等高线近似于一簇相互平行的直线段,该值越小表明舰载机的俯仰姿态改变量就越小,因而其逃逸复飞特性也就越好。基于迎角增量的约束要求,可以确定各着舰重量下飞机的最小进舰速度。
4) 舰载机的着舰下滑角一般取为固定值-3.5°,因此飞机着舰时的俯仰角与下滑配平时的迎角一一对应,变化规律较为明确,即进舰速度越大、着舰重量越轻,则着舰时的俯仰角就越小,如图 5(c)所示。从逃逸复飞安全性角度出发,为了避免前起落架先触舰的情况发生,应当对着舰时俯仰角的下限值进行约束,因此也就能够确定各着舰重量下飞机的最大进舰速度。
2.4 参数适配包线及其计算方法本文所提出的参数适配包线,指的是满足一定舰载机飞行状态(如下滑角)、航母运动状态(如航母航速)和逃逸复飞安全性要求的舰载机着舰重量、进舰速度的组合情况,因而可以为机舰适配性研究和作战使用条件确定提供量化的评估参考。
参数适配包线的计算方法如下:
步骤1 按照2.2节和2.3节的方法,通过数字虚拟飞行仿真计算,获得舰载机在不同着舰重量和进舰速度下逃逸复飞性能评定参数的等高线图。
步骤2 对于每一项逃逸复飞性能的评定参数,确定其安全性判定标准,从而在性能等高线图中求出对应的边界约束。
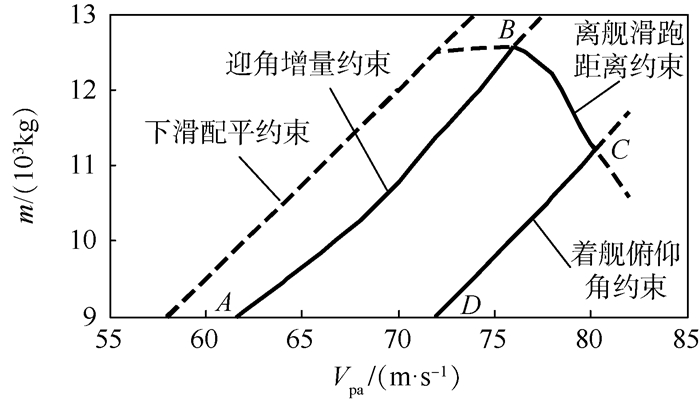
步骤3 求取3条边界约束的交集后,就能够得到满足全部逃逸复飞安全要求的参数适配包线,如图 6所示。图中:AB段为迎角增量的约束,
|
| 图 6 逃逸复飞的参数适配包线 Fig. 6 Parameter suitability envelope for bolter |
其决定了参数适配包线的左边界;BC段为离舰滑跑距离的约束,其决定了参数适配包线的上边界;CD段为着舰时俯仰角的约束,其决定了参数适配包线的右边界。
3 参数适配包线的影响因素1) 舰载机在实际执行作战任务时,其燃油消耗和武器装载使用等均存在一定的不确定性,故其着舰时的重心位置等都可能偏差理想设计状态。重心位置的前后变化将直接影响飞机的纵向力矩特性,既会改变飞机进舰下滑时的配平飞行状态,也会影响其逃逸复飞滑跑时的抬前轮特性。美军研究中也指出,进行逃逸复飞飞行试验时应当特别关注飞机前后重心的配置问题[1]。
2) 航母航速是船舶设计部门最为关注的机舰适配参数之一,除了分析典型航速(20 kn)下的参数适配包线外,还十分关注零甲板风条件(即航速为零时)的机舰适配关系,因为它可以表征极限状态的使用条件。
3) 由于第2节建立参数适配包线时尚未考虑航母甲板运动的影响,只能反映平稳海况下的机舰参数适配关系。随着航母编队走向远海,高海况条件也是必然面临的作战使用环境,在舰载机逃逸复飞安全性研究时也必需考虑海况条件的影响。
综上所述,本节将进一步讨论分析舰载机重心位置、航母航速及海况等级等3个因素对参数适配包线的影响,便于发现舰载机总体方案设计和机舰适配特性中可能存在的问题,为方案的设计改进、作战使用条件的论证分析等提供参考。
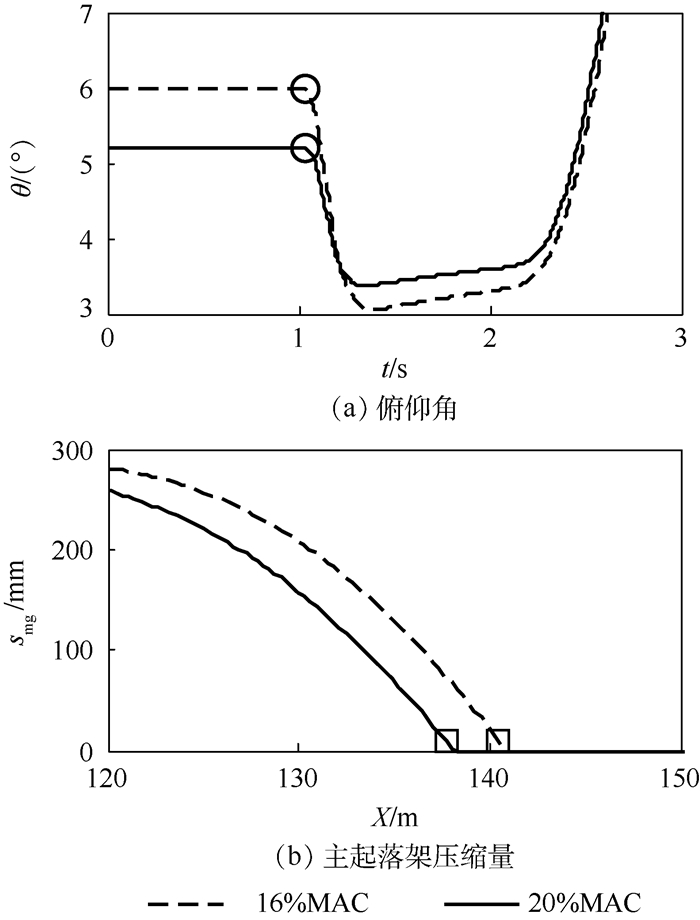
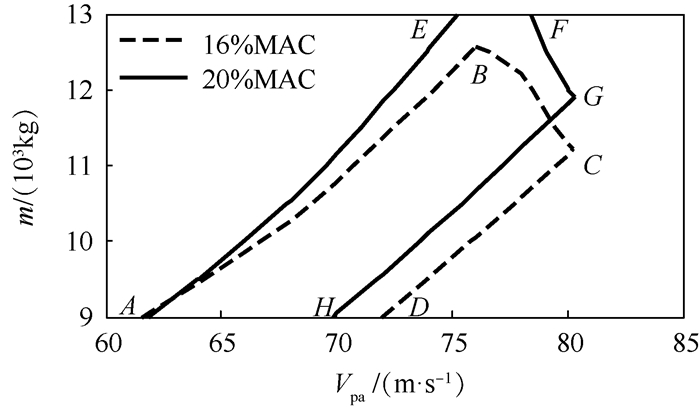
3.1 舰载机重心位置通过改变仿真模型的初始计算条件,本文对比了重心位置分别为16%MAC和20%MAC时的逃逸复飞仿真曲线,并且计算获得这2个重心位置所对应的参数适配包线,仿真结果如图 7和图 8所示。舰载机的重心位置后移后,其进舰下滑时的配平迎角将有所减小,因此着舰俯仰角由6°减小至5.2°。同时,飞机的抬前轮特性有所提高,离舰滑跑距离由139 m缩短至136 m。重心位置后移对参数适配包线的影响如下:着舰俯仰角的约束边界向左移动,由CD段变为GH段;离舰滑跑距离的约束边界向上移动,由BC段变为FG段;迎角增量的约束边界略微向左移动,由AB段变为AE段。
|
| 图 7 不同重心位置时的仿真曲线 Fig. 7 Simulation curves with different positions of center of gravity |
|
| 图 8 重心位置对参数适配包线的影响 Fig. 8 Effect of position of center of gravity on parameter suitability envelope |
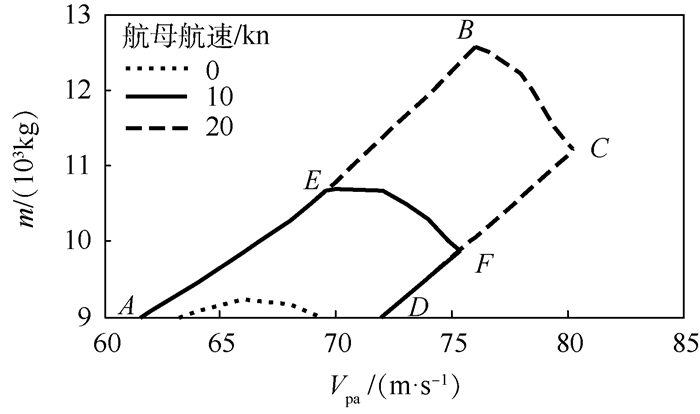
对于舰载机的逃逸复飞任务而言,航母航速减小后,机舰之间在水平方向上的相对速度增大,在同样的飞行员反应和操纵时间内,飞机的甲板滑跑距离就有所增大,因此满足离舰滑跑距离约束限制的参数适配范围相应减小,如图 9所示。
|
| 图 9 航母航速对参数适配包线的影响 Fig. 9 Effect of carrier velocity on parameter suitability envelope |
计算结果表明:航母航速由20 kn减小至10 kn后,适配的最大着舰重量由12.5×103 kg减小为10.7×103 kg,同时适配的最大进舰速度由80 m/s减小为75 m/s。零甲板风条件下,参数适配包线进一步缩小,此时应当严格约束飞机的进舰速度与着舰重量,提高逃逸复飞的安全。
3.3 着舰海况等级在不同的着舰海况等级下,航母甲板的垂荡和俯仰运动的幅值不同,这将影响舰载机的逃逸复飞特性,主要体现在触舰时刻飞机在甲板上的位置、起落架载荷及逃逸复飞的轨迹等[10]。在现有的研究中,一般是根据甲板运动的数学模型,选取典型的初始相位值进行仿真计算,从而分析最有利和最不利的极限状态条件。然而,这样的定性处理方式只能适用于特定的甲板运动条件,无法体现出实际情况下初始相位具有随机性的特点。
因此,本文根据式(5)和表 1所建立的甲板运动模型,随机选取100组不同的甲板运动初始相位组合,在图 6所示的参数适配包线内进行逃逸复飞的数字虚拟飞行仿真计算,并以逃逸复飞成功率pbo作为评价指标,从而定量地建立起不同海况等级与逃逸复飞参数适配包线的联系,计算步骤如下:
步骤1 随机生成1组甲板运动的初始相位组合,例如(φϕc, φθc, φΔzc)=(18°, 126°, 144°),那么按式(5)计算后可分别获得对应初始相位下,4级海况和6级海况条件的甲板运动参数的时间历程。重复这一过程,可以获得200组甲板运动参数的时间历程(4级海况和6级海况各100组),作为步骤2仿真时的计算输入。
步骤2 在图 6所示的参数适配包线内,任意选取1种舰载机进舰速度和着舰重量的参数组合,例如(m, Vpa)=(11×103 kg, 72 m/s),再结合已有的200组甲板运动参数进行仿真,可以得到4级海况和6级海况下的仿真算例各100组。
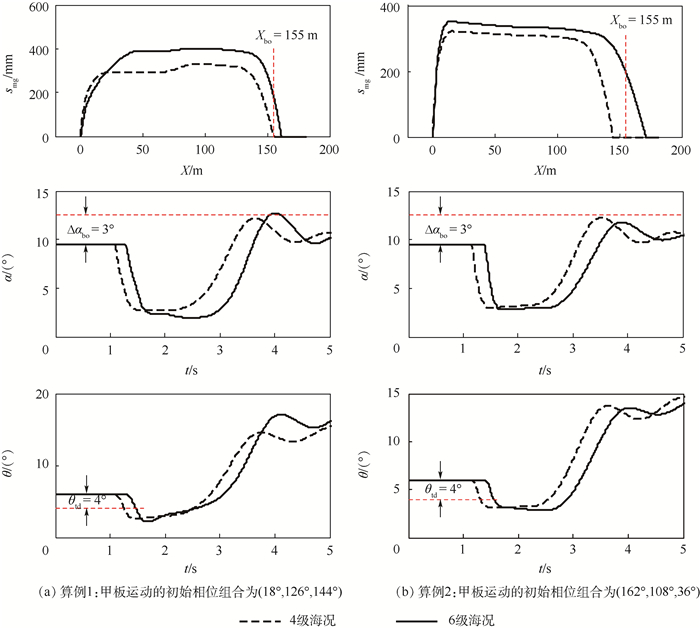
步骤3 对仿真算例进行甄别,排除逃逸复飞的失败算例(见图 10)后,可以计算逃逸复飞成功率:pbo(11×103 kg, 72 m/s, 4级海况)=70%, pbo(11×103 kg, 72 m/s, 6级海况)=55%。
|
| 图 10 不同海况等级下的逃逸复飞算例 Fig. 10 Bolter simulation samples under different sea states |
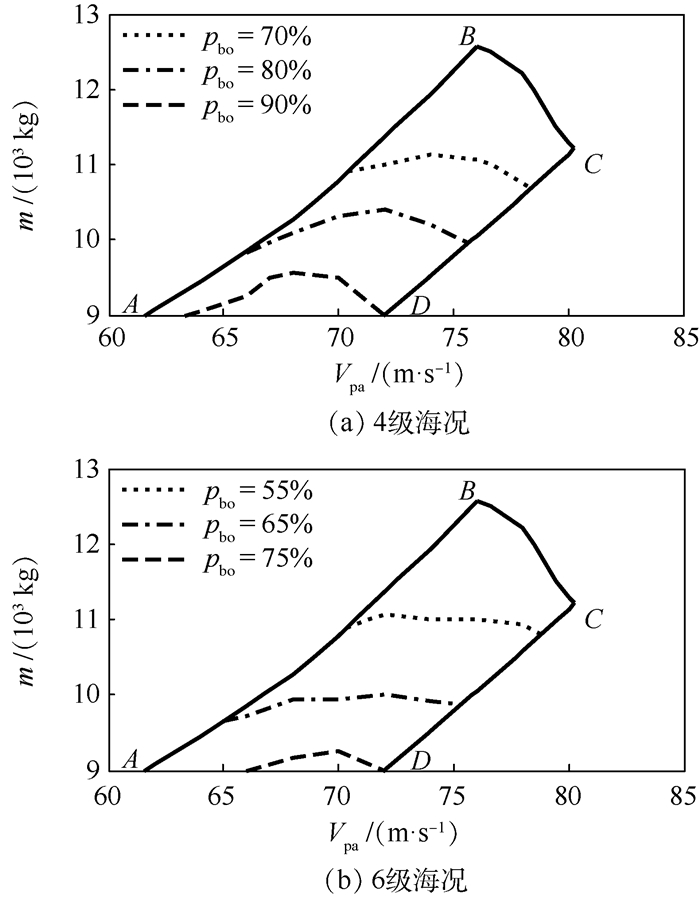
步骤4 对于参数适配包线内的每一组进舰速度和着舰重量的参数组合,重复步骤2和步骤3,并且将参数适配包线内逃逸复飞成功率相同的点连线后,得到了不同海况等级下舰载机的逃逸复飞成功率,如图 11所示。
|
| 图 11 不同海况等级下的逃逸复飞成功率 Fig. 11 Bolter success rate under different sea states |
图 10给出了2组逃逸复飞仿真算例的对比,根据飞机的离舰滑跑距离(可由主起落架压缩量smg进行计算,smg由零开始增大再减小至零的过程即对应了飞机着舰、滑跑和离舰的逃逸复飞过程)、迎角和俯仰角仿真曲线,可以判断逃逸复飞是否成功。图中所标注的“Xbo=155 m”“Δαbo=3°”“θtd=4°”分别表示对应参数的安全性判定要求。在算例1中(见图 10(a)),飞机离舰滑跑距离、迎角增量、着舰俯仰角3个参数在4级海况条件时分别为154 m、2.7°、6°,在6级海况条件时分别为160 m、3.1°、6°。基于离舰滑跑距离小于155 m、迎角增量小于3°、着舰俯仰角大于4°的安全性判定要求,因此判断4级海况下逃逸复飞成功,6级海况下逃逸复飞失败。同理可判断在算例2中(见图 10(b)),由于飞机在6级海况下的离舰滑跑距离过大(约为170 m),因此飞机逃逸复飞失败。
一般来说,如果从飞机离舰后的航迹变化角度分析,甲板具有上升的运动趋势是有利的,因为此时飞机具有更大的初始爬升速度。但在逃逸复飞任务中,由于飞行员更关注飞机是否能够在到达甲板末端前就完成复飞拉起,因此只有当飞机的爬升速度大于其所处位置的甲板上升速度,才能够表征飞机完成了逃逸复飞。从这一角度来看,甲板具有上升的运动趋势时未必会给逃逸复飞带来有利的影响,即飞机需要获得更大的升力和爬升速度才能克服甲板的上升运动,进而脱离甲板开始爬升。仿真计算结果表明,当甲板具有上升的运动趋势时,飞机逃逸复飞的离舰滑跑距离与迎角增量均有所增大。
如图 11所示,当考虑了不同海况等级下的甲板运动影响后,原参数适配包线内的每一着舰重量、进舰速度组合均对应了一个逃逸复飞的成功率。仿真计算结果表明:由于高海况条件下,甲板运动的幅值增大,飞机更容易出现逃逸复飞失败的情况。与4级海况条件相比,6级海况条件下舰载机的逃逸复飞成功率平均下降了约15%。因此,为了提高舰载机的逃逸复飞安全,建议根据pbo进一步缩小参数适配包线,并作为设计使用条件时参考。
4 结论1) 离舰滑跑距离、逃逸复飞段最大迎角相对进舰配平迎角的增量和着舰时的俯仰角等3个评定参数可用于分析舰载机的逃逸复飞特性。数字虚拟飞行的仿真计算结果表明,在每一设计着舰重量下均对应存在一个最佳的进舰速度范围,从而使逃逸复飞的离舰滑跑距离最短;同时,最大的迎角增量、着舰时的俯仰角分别决定了满足安全逃逸复飞要求时的最小、最大进舰速度。
2) 适配包线能够表征满足逃逸复飞安全要求的着舰重量、进舰速度的组合情况,其边界由对应的逃逸复飞评定参数确定。舰载机重心位置变化将使参数适配包线的边界位置和范围发生改变,但边界形状基本不变。航母航速减小将显著缩小参数适配包线。
3) 本文算例飞机具有零甲板风条件下的安全逃逸复飞能力。在6级海况条件下,其逃逸复飞的成功率较4级海况条件下降了约15%。建议以定量计算获得的逃逸复飞成功率作为评价指标,进一步缩小参数适配包线作为设计使用条件,从而提高舰载机逃逸复飞的安全性。
| [1] |
U.S.Department of Defense.Air vehicle joint service specification guide: JSSG-2001A[S].Patuxent River: Naval Air Systems Command, 2002: D-40.
|
| [2] |
杨一栋, 江驹, 张宏涛, 等. 着舰安全与复飞技术[M]. 北京: 国防工业出版社, 2013: 116-150. YANG Y D, JIANG J, ZHANG H T, et al. Safety and waveoff technologies in carrier landing[M]. Beijing: National Defense Industry Press, 2013: 116-150. (in Chinese) |
| [3] |
RUDOWSKY T, COOK S, HYNES M, et al.Review of the carrier approach criteria for carrier-based aircraft.Phase I: Final report[R].Patuxent River: Naval Air Warfare Center Aircraft Division, 2002.
|
| [4] |
杨一栋. 舰裁机进场着舰规范评估[M]. 北京: 国防工业出版社, 2006: 123-124. YANG Y D. Review of the carrier approach criteria[M]. Beijing: National Defense Industry Press, 2006: 123-124. (in Chinese) |
| [5] |
王永庆, 罗云宝, 王奇涛, 等. 面向机舰适配的舰载飞机起降特性分析[J]. 航空学报, 2016, 37(1): 269-277. WANG Y Q, LUO Y B, WANG Q T, et al. Carrier suitability-oriented launch and recovery characteristics of piloted carrier-based aircraft[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(1): 269-277. (in Chinese) |
| [6] |
励缨, 温玮, 金长江. 舰载飞机逃逸复飞动力学特性研究[J]. 飞行力学, 1994, 12(2): 1-9. LI Y, WEN W, JIN C J. The study of dynamic character of bolting and going-around for carrier aircraft[J]. Flight Dynamics, 1994, 12(2): 1-9. (in Chinese) |
| [7] |
崔坤林, 胡国才, 罗云宝. 舰载飞机纵向逃逸性能仿真研究[J]. 海军航空工程学院学报, 2009, 24(4): 435-439. CUI K L, HU G C, LUO Y B. Simulated investigation for carrier-based airplane longitudinal go-around performance[J]. Journal of Naval Aeronautical and Astronautical University, 2009, 24(4): 435-439. DOI:10.3969/j.issn.1673-1522.2009.04.018 (in Chinese) |
| [8] |
史卫民, 韩维, 李辉青. 基于ADAMS/Aircraft的舰载机逃逸性能分析[J]. 海军航空工程学院学报, 2010, 25(5): 481-484. SHI W M, HAN W, LI H Q. The carrier-based aircraft bolter analysis based on ADAMS/Aircraft[J]. Journal of Naval Aeronautical and Astronautical University, 2010, 25(5): 481-484. DOI:10.3969/j.issn.1673-1522.2010.05.001 (in Chinese) |
| [9] |
陶杨, 韩维, 李军亮. 舰载机逃逸过程动力学研究[J]. 计算机仿真, 2015, 32(3): 77-80. TAO Y, HAN W, LI J L. Dynamic research of carrier aircraft's escaping[J]. Computer Simulation, 2015, 32(3): 77-80. DOI:10.3969/j.issn.1006-9348.2015.03.017 (in Chinese) |
| [10] |
段萍萍, 聂宏, 魏小辉. 飞机触舰后逃逸复飞性能分析[J]. 中国机械工程, 2014, 25(9): 1225-1231. DUAN P P, NIE H, WEI X H. Bolting and go-around performance analysis of carrier-based aircraft[J]. China Mechanical Engineering, 2014, 25(9): 1225-1231. DOI:10.3969/j.issn.1004-132X.2014.09.017 (in Chinese) |
| [11] |
张声伟, 段卓毅, 耿建中, 等. 阻拦索断裂对螺旋桨舰载机着舰安全影响数值分析[J]. 航空学报, 2019, 40(4): 622293. ZHANG S W, DUAN Z Y, GENG J Z, et al. Carrier suitability-oriented launch and recovery characteristics of piloted carrier-based aircraft[J]. Acta Aeronautica et Astronautica Sinica, 2019, 40(4): 622293. (in Chinese) |
| [12] |
国防科学技术工业委员会.舰载飞机强度和刚度规范地面载荷: GJB 2753-96[S].北京: 中国标准出版社, 1997. The Commission of Science, Technology and Industry for National Defense.Carrier-based airplane strength and rigidity specification ground loads: GJB 2753-96[S].Beijing: Standards Press of China, 1997(in Chinese). |
| [13] |
SCHARL J, MAVRIS D N, BURDUN I Y.Use of flight simulation in early design: Formulation and application of the virtual testing and evaluation methodology: AIAA-2000-5590[R].Reston: AIAA, 2000.
|
| [14] |
《飞机设计手册》总编委会. 飞机设计手册第14册起飞着陆系统设计[M]. 北京: 航空工业出版社, 2002: 96-98. The Chief Committee of Aircraft Design Manual. Aircraft design manual.Volume 14:Takeoff and landing system design[M]. Beijing: Aviation Industry Press, 2002: 96-98. (in Chinese) |
| [15] |
高金源, 李陆豫, 冯亚昌. 飞机飞行品质[M]. 北京: 国防工业出版社, 2003: 139-143. GAO J Y, LI L Y, FENG Y C. Aircarft handing qualities[M]. Beijing: National Defense Industry Press, 2003: 139-143. (in Chinese) |
| [16] |
ZAAL P M, POOL D M, BRUIN J, et al. Use of pitch and heave motion cues in a pitch control task[J]. Journal of Guidance, Control and Dynamics, 2009, 32(2): 366-377. DOI:10.2514/1.39953 |
| [17] |
陈俊平, 王立新. 低能量状态对飞行安全的危害及改出方法[J]. 航空学报, 2017, 38(8): 61-71. CHEN J P, WANG L X. Hazards of low energy state to flight safety and recovery methods[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(8): 61-71. (in Chinese) |
| [18] |
彭競.舰载飞机进舰着舰的自动引导和控制研究[D].北京: 北京航空航天大学, 2001: 33-41. PENG J.Research on the automatic guide and control of carrier-based airplane approach and landing[D].Beijing: Beihang University, 2001: 33-41(in Chinese). http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y425400 |
| [19] |
DENISON N A.Automated carrier landing of an unmanned combat aerial vehicle using dynamics inversion[D].Wright-Patterson Air Force Base: Air Force Institute of Technology, 2007: 42-43.
|



