非线性系统的控制问题一直是国内外研究的热点。目前非线性控制已与自适应控制、模糊控制和神经网络等学科紧密结合[1-4]。反步法(backstepping)是解决非线性系统控制问题的重要方法之一,是一种递归设计算法,它是由Lozano、Brogliato[5]和Kokotovic[6]于1992年所提出的[5-6],经过二十几年的发展,已逐渐成熟[7-8],在工业生产、航空航天等领域均有广泛应用[9-11]。
反步法主要是通过递归的方法,寻找使闭环系统稳定的Lyapunov函数,从而得到反馈控制器。反步法一大特点是递归。为了完成递归,保证闭环系统的稳定性,反步法需要系统满足在某次递归时,系统的Lyapunov函数仅包含此前递归设计中所稳定的状态。这对于系统本身的结构提出了一定的要求。满足反步法设计要求的系统称为严格反馈型系统。
本文提出了一种控制方法,对于某一类反馈型非线性系统,无须再满足以上要求,从而改为满足一种有界要求。并且利用一个飞机纵向运动的算例说明了该方法的有效性。
1 问题的提出考虑如下反馈型单输入单输出系统:

|
(1) |
式中:x=[x1 x2 … xn]T为系统状态;u为系统输入;y为系统输出;ϕ为关于状态x的非线性连续函数向量,满足局部Lipschitz条件;b=[0 … 0 1]T;c=[1 0 … 0];A为n×n维矩阵。
由于传统的反步法所要求的系统为严格反馈型系统,对于式(1)这样的系统,要求A阵对角线及以下元素都为0。除此之外,反步法所要求的ϕi仅仅是关于x1, x2, …, xi的非线性函数。而在实际应用中,对象常常很难全部满足以上要求。此时无法利用反步法实现对系统的控制。所以研究针对这类系统的控制方法有重要意义。现研究一个无法满足以上要求的低阶的系统,A和ϕ具有以下形式:
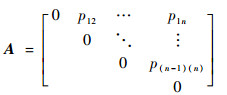
|
(2) |

|
(3) |
设计出使系统镇定的非线性控制器,完成系统的跟踪问题。
2 控制器的设计设误差函数e=[e1 e2 … en]T:
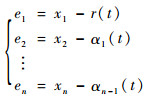
|
(4) |
式中:αi-1(t)为状态xi的期望轨迹;r(t)为指令信号,也即状态x1的期望轨迹。r(t)应满足二阶可导,且r(t)及其导数应满足有界。
定理1 形如式(1)的三阶系统,若系统满足:
1) 
2) 设Dc为R上一闭区间,当x1∈Dc, x2, x3∈R时,ϕ1和ϕ2有界。
当系统的输入定义为
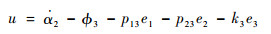
|
(5) |
式中:

|
(6) |
其中:k1、k2和k3为可调的参数,是正实数。则该系统镇定,系统的所有状态及控制信号有界。并且在理论上,跟踪误差最终趋于0。
定理2 形如式(1)的四阶系统,若系统满足:
1) 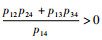
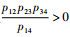
2) 设Dc为R上一闭区间,当x1∈Dc,x2, x3, x4∈R时,ϕ1、ϕ2和ϕ3有界。
当系统的输入定义为
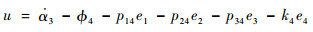
|
(7) |
式中:

|
(8) |
其中:k1、k2、k3和k4为可调的参数,是正实数。则该系统镇定,系统的所有状态及控制信号有界。并且在理论上,跟踪误差最终趋于0。
为了证明上述定理,首先论证2个引理。
引理1[12](LaSalle不变性原理) 设f(x)是定义域Dd⊂Rn上的局部Lipschitz函数,Ω⊂Dd是一个紧集,并且是关于
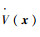
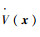
由上述引理1,可以证明以下引理2。
引理2 考虑如下n维系统:
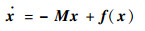
|
(9) |
式中:f(x)为定义在Rn上的n维函数向量,满足Lipschitz条件。

|
(10) |
若满足:
1) M的所有特征值均大于0。
2) M的特征空间维数等于n。
3) 存在常数cf,使得任意x∈Rn,都有‖f(x)‖≤cf。
则系统对于任意的初始状态x(0),t>0时‖x(t)‖都满足有界。
证明 由于f(x)的2-范数有界,其各分量也都有界。所以存在实数序列{an}和{bn},使得ai<fi(x)<bi。设xi为x不包含xi分量的向量,即xi=[x1 … xi-1 xi+1 … xn]T,因此有
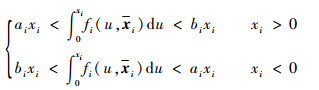
|
(11) |
取

|
(12) |
用2个函数hmin(x)和hmax(x)来表示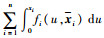

|
(13) |
式中:
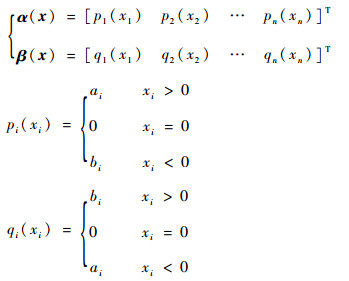
|
注意,α和β并不连续,但hmin(x)和hmax(x)是连续的。令

|
(14) |
所以有

|
(15) |
V(x)对t求导:
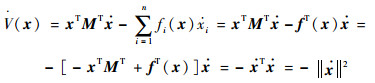
|
(16) |
可知, 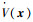
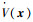
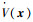
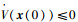
设M的n个特征值为λ1, λ2, …, λn,由于M的特征空间维数为n,所以有n个线性无关的特征向量。因此对于任意非零向量x∈Rn,总是存在n个实数c1, c2, …, cn,使得
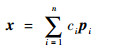
|
(17) |
式中:pi为对应特征值λi的特征向量。设λmin(M)表示M的最小特征值,由式(14)、式(17),有
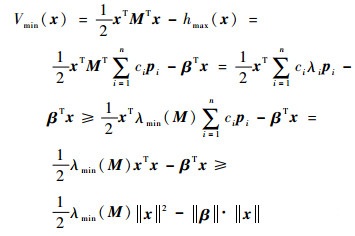
|
(18) |
‖x‖→∞时,‖β‖为实数,λmin(M)>0,因此Vmin(x)→∞。Vmin(x)是径向无界的,对于Vmax(x)也有相同的结果。又由式(15),可以得出V(x)也是径向无界的。所以对于任意一个l>0,集合Ω={x∈Rn|V(x)≤l}都是有界的。根据Ω的定义,它又是一个闭集,故Ω是一个紧集。设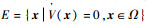

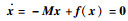
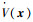
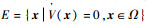
接下来仅证明定理2,定理1的证明方法与定理2类似。
证明 如式(1)的四阶系统状态方程可以写为
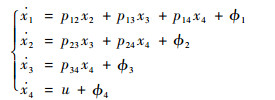
|
(19) |
考虑由误差函数e构成的系统,取正定函数V(e):

|
(20) |
式中:I为单位阵。则

|
(21) |
对V(e)求导,并且代入式(4)、式(19)得
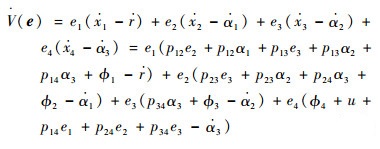
|
(22) |
利用Lyapunov逆向法,先令

|
(23) |
最后令

|
(24) |
则可以使得

|
(25) |
且V(e)径向无界,则由误差函数e构成的系统全局渐近稳定。也就有当t→∞,有e→0,即x→[r α1 α2 α3]T。注意,此时已有x1有界。若能证明函数α1、α2和α3在t→∞时收敛,则有系统镇定,所有状态均有界。
由式(23),消去α3得

|
(26) |
式中:g1和g2为关于e和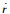
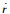
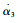
机体轴下,某固定翼飞机纵向运动的动力学方程与运动学方程分别为[13]

|
(27) |
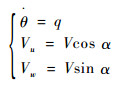
|
(28) |
式中:V为飞行速度;Vu和Vw分别为机体轴下飞行速度在x轴和z轴的分量;D为阻力;L为升力;T为发动机推力;M为俯仰力矩;α为飞机迎角;θ为速度倾角;q为俯仰角速率;m为飞机的质量;Iy为绕y轴的转动惯量;zT为发动机推力线到重心的距离;ϕT为推力线与机体轴的安装角。
做以下假设:
假设1 T为常数,即油门杆位置不变。
假设2 V为常数,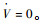
式(27)、式(28)可以化为
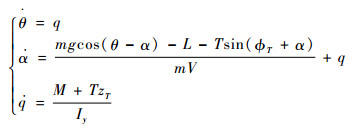
|
(29) |
式中:

|
其中:ρ为飞机所在高度的空气密度;Sw为机翼面积;cA为平均气动弦长;CL和CM分别为升力系数和俯仰力矩系数。
假设3 忽略升降舵对升力的作用。由于控制舵面的贡献主要是产生转动力矩,其生成的气动力很小。
因此升力系数可以写为
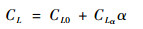
|
(30) |
式中:CL0为零升力系数;CLα为受迎角α影响的系数。
俯仰力矩系数写为两部分构成:一部分由控制升降舵偏角δe直接作用,另一部分由飞机当前状态决定。
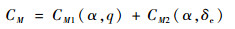
|
(31) |
式中:CM2=-cδ(δe+α)[14],cδ为关于δe的一个正的常数;CM1由插值得出,不必知道其函数表达式。
设x=[θ α q]T,u=δe,系统可以写为
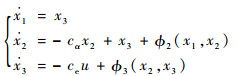
|
(32) |
式中:cα和ce都为正实数。cα、ce和ϕ2、ϕ3表达式分别为
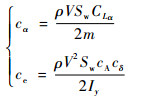
|
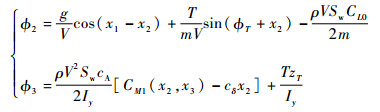
|
可以看出, ϕ2满足定理1中的有界条件。作变量代换z=Tx:
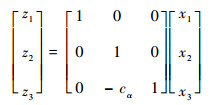
|
(33) |
式(32)变为

|
(34) |
再设
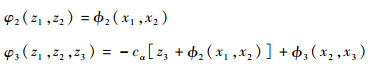
|
式(34)变为
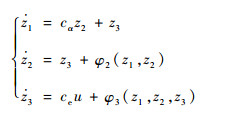
|
(35) |
显然, φ2也满足定理1中的有界条件。系统(35)满足定理1所有条件,因此根据定理1可以设计出控制器。
以某喷气式飞机为例,马赫数Ma=1.2,飞行高度H=16 764 m,将飞机及大气的各数据[13-15]代入系统,并且在MATLAB的Simulink模块下进行仿真验证。并用低通滤波器和限幅器对输入信号舵偏角u进行过滤。
1) 阶跃信号
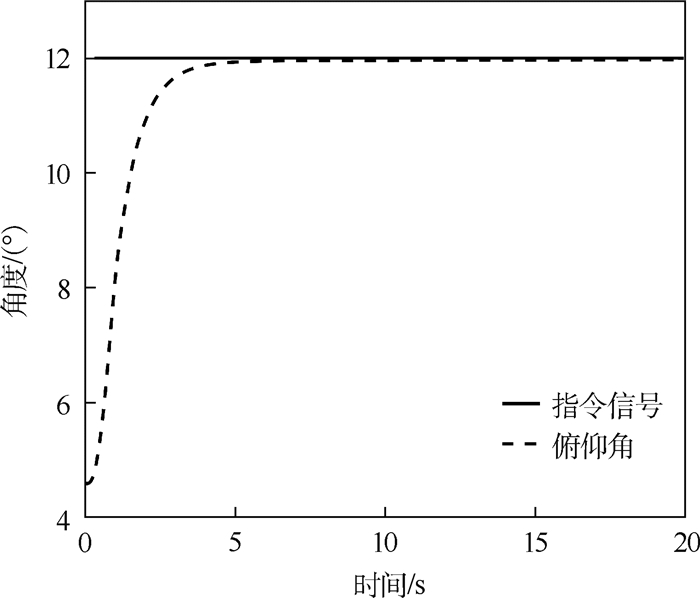
对于给定的阶跃值r=12°,设计参数为k1=5, k2=10, k3=1,飞机俯仰角变化如图 1所示。
|
| 图 1 阶跃信号下俯仰角变化曲线 Fig. 1 Pitch angle change curve under step signal |
由图 1可以看出,俯仰角与指令信号的误差收敛的非常快,在t=5 s时几乎完成了对指令的跟踪,并且稳态误差很小。阶跃信号下系统的3个状态变化如图 2所示。

|
| 图 2 阶跃信号下系统状态变化曲线 Fig. 2 System states change curves under step signal |
由图 2可以看出,系统的3个状态最终均收敛。俯仰角和俯仰角速率收敛较快,迎角收敛于5.6°,故飞机将以6.4°的速度倾角爬升。
2) 正弦信号
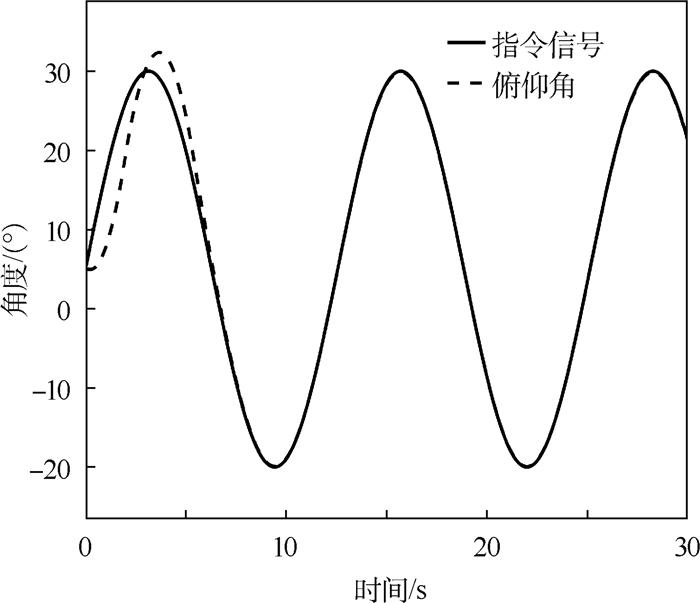
对于正弦信号r=25°sin(0.5t)+5° ,飞机的俯仰角变化如图 3所示。
|
| 图 3 正弦信号下俯仰角变化曲线 Fig. 3 Pitch angle change curve under sinusoidal signal |
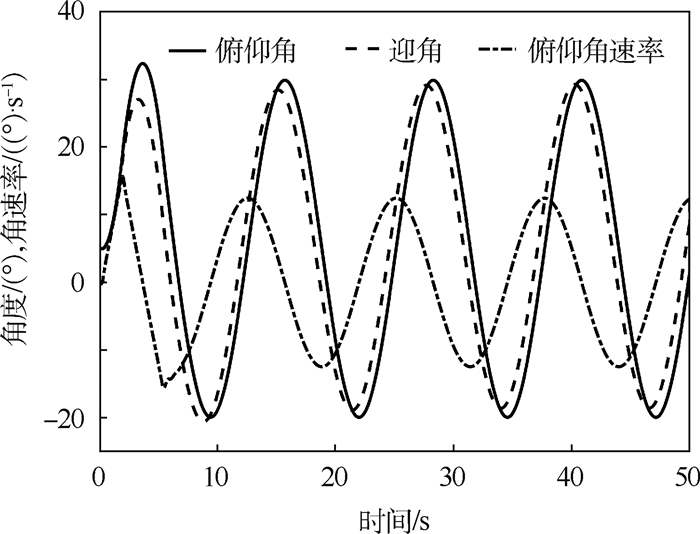
俯仰角在经过半个周期后,已经完成了对指令的跟踪。这说明对于俯仰角剧烈变化的情形,控制器依然能够有效完成跟踪。正弦信号下系统的3个状态变化如图 4所示。
|
| 图 4 正弦信号下系统状态变化曲线 Fig. 4 System states change curves under sinusoidal signal |
从图 4中可以看出,系统状态均随指令信号保持稳定的周期变化。
4 结论本文针对一类反馈型非线性系统,在系统低阶的情况下,提出了一种控制方法。该方法能保证系统所有状态即控制信号都有界。以某固定翼飞机纵向运动为例进行仿真,对于阶跃信号和大幅度剧烈变化的正弦信号,仿真结果说明:
1) 控制器能够保证闭环系统的稳定性,所有状态全部有界。
2) 控制器可以有效的完成跟踪任务,通过调整设计参数,跟踪误差可以收敛于满足需要的小范围内。
3) 系统输出的收敛速度非常快。
后续的工作将专注于控制系统的鲁棒性,以及将控制方法推广至高阶系统。
| [1] |
WANG C, WEN C, LIN Y. Adaptive actuator failure compensation for a class of nonlinear systems with unknown control direction[J]. IEEE Transactions on Automatic Control, 2016, 62(1): 385-392. |
| [2] |
CAI J, WEN C, SU H, et al. Adaptive backstepping control for a class of nonlinear systems with non-triangular structural uncertainties[J]. IEEE Transactions on Automatic Control, 2016, 62(10): 5220-5226. |
| [3] |
FURQON R, CHEN Y J, TANAKA M, et al. An SOS-based control Lyapunov function design for polynomial fuzzy control of nonlinear systems[J]. IEEE Transactions on Fuzzy Systems, 2017, 25(4): 775-787. DOI:10.1109/TFUZZ.2016.2578339 |
| [4] |
ZHANG W, LI C, HUANG T, et al. Stability and synchronization of memristor-based coupling neural networks with time-varying delays via intermittent control[J]. Neurocomputing, 2016, 173(P3): 1066-1072. |
| [5] |
LOZANO R, BROGLIATO B. Adaptive control of robot manipulators with flexible joints[J]. IEEE Transactions on Automatic Control, 1992, 37(2): 174-181. DOI:10.1109/9.121619 |
| [6] |
KOKOTOVIC P. The joy of feedback:Nonlinear and adaptive[J]. IEEE Control Systems Magazine, 1992, 12(3): 7-17. DOI:10.1109/37.165507 |
| [7] |
KOKOTOVIC P, ARCAK M. Constructive nonlinear control:A historical perspective[J]. Automatica, 2001, 37(5): 637-662. DOI:10.1016/S0005-1098(01)00002-4 |
| [8] |
QU Z. Robust control of nonlinear uncertain systems under generalized matching conditions[J]. IEEE Transactions on Automatic Control, 1993, 40(8): 1453-1460. |
| [9] |
HOU Z G, ZOU A M, CHENG L, et al. Adaptive control of an electrically driven nonholonomic mobile robot via backstepping and fuzzy approach[J]. IEEE Transactions on Control Systems Technology, 2009, 17(4): 803-815. DOI:10.1109/TCST.2009.2012516 |
| [10] |
李海涛, 闫斌. 基于自适应反步的DGMSCMG框架伺服系统控制方法[J]. 北京航空航天大学学报, 2016, 42(4): 703-710. LI H T, YAN B. Adaptive backstepping control method used in DGMSCMG gimbal servo system[J]. Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(4): 703-710. (in Chinese) |
| [11] |
方一鸣, 任少冲, 王志杰, 等. 永磁同步电动机转速自适应模糊Backstepping控制[J]. 电机与控制学报, 2011, 15(6): 97-102. FANG Y M, REN S C, WANG Z J, et al. Adaptive fuzzy Backstepping control for speed of permanent magnet synchronous motor[J]. Electric Machines and Control, 2011, 15(6): 97-102. DOI:10.3969/j.issn.1007-449X.2011.06.017 (in Chinese) |
| [12] |
LASALLE J P. The extent of asymptotic stability[J]. Proceedings of the National Academy of Sciences of the United States of America, 1960, 46(3): 363-365. DOI:10.1073/pnas.46.3.363 |
| [13] |
徐军, 杨亚炜. 飞机电传操纵系统[M]. 北京: 北京理工大学出版社, 2018: 65-74. XU J, YANG Y W. Aircraft fly-by-wire system[M]. Beijing: Beijing Institute of Technology Press, 2018: 65-74. (in Chinese) |
| [14] |
XU H, MIRMIRANI M, IOANNOU P.Robust neural adaptive control of a hypersonic aircraft: AIAA-2003-5641[R].Reston: AIAA, 2003.
|
| [15] |
WANG Q, STENGEL R F. Robust nonlinear control of a hypersonic aircraft[J]. Journal of Guidance, Control, and Dynamics, 2000, 23(1): 15-26. |



