2. 航天工程大学 太空安全研究中心, 北京 101416
2. Space Security Research Center, Space Engineering University, Beijing 101416, China
目标的遥感测量可有效获取目标运动特性,有助于对目标飞行试验效果进行评估。目标的轨迹重建是遥感测量系统获取目标信息的关键技术,目标的空间轨迹及运动参数通常需要双平台观察,并采用双目视觉方法进行重建,这提高了观测系统的复杂度,例如,天基红外预警系统的高轨部分包括4颗静止轨道卫星和2颗大椭圆轨道卫星,低轨部分由21~28颗小型卫星组成[1],其部署和维护成本极大,因此,在实际观测系统中,常常只进行单平台的观测[2]。这对单平台观测条件下的目标运动特性反演提出了迫切的需求。研究人员对单星条件下的目标运动参数估计方法进行了较多的研究,参数估计方法主要包括基于弹道模板的弹道参数估计方法[3-4]和基于目标运动特性建模的参数估计方法[5]。为提高估计精度,研究人员进一步将目标动力特征的先验知识应用于单星弹道导弹参数估计中[6],但目前基于单星的目标运动特性反演方法仍存在反演精度较低的问题,该类方法还不足以支撑目标参数测量的需求。因此,本文结合实际应用中所能获得的目标先验知识,研究具有更高估计精度的目标特性反演方法。
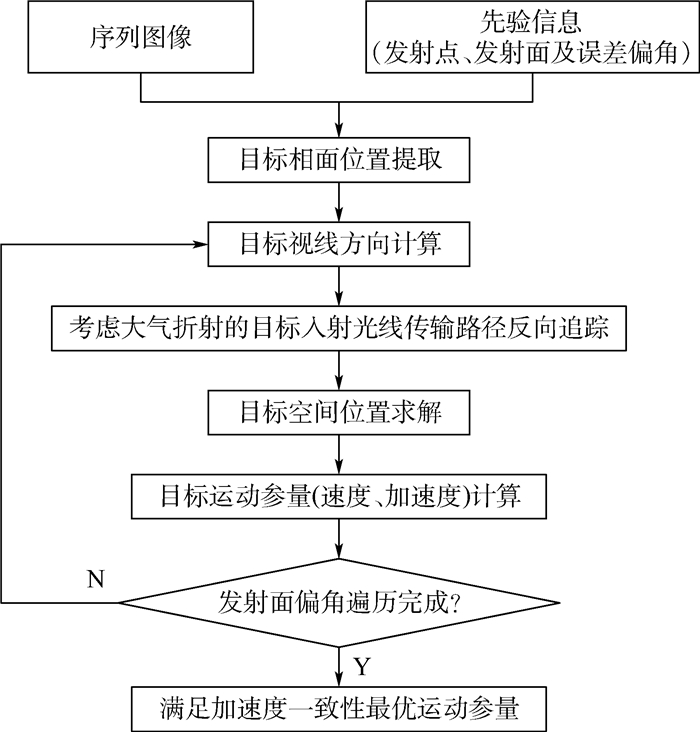
1 单平台目标运动特性反演模型在单平台下目标轨迹重建思路为:对获取的序列图像进行目标的提取,确定目标在图像上的位置,获得不同成像时刻的目标图像位置。对每一个目标位置,根据对应的成像参数,计算目标视线的方向矢量,从成像器所在位置出发,考虑大气折射,对目标视线的光学路径进行反向追踪,追踪路径与发射面的交点即为目标的空间位置,并通过多帧图像反演获得的序列目标空间位置进行拟合处理,修正目标空间位置,反演目标运动参数。计算过程中所需的发射面参数可根据经验设定,也可以由其他计算方式获得。单平台下成像目标运动特性反演的总流程如图 1所示。
|
| 图 1 实现方案总流程图 Fig. 1 General flowchart of implementation scheme |
通过目标的提取,获得成像时刻在相机成像的第k帧图像上目标的位置p=(xk, yk)T,图像行数r及列数c,以及像元视场角ϕpixel,进而可求出该位置对应于目标相对于光轴的偏角(αx, αy)为
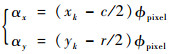
|
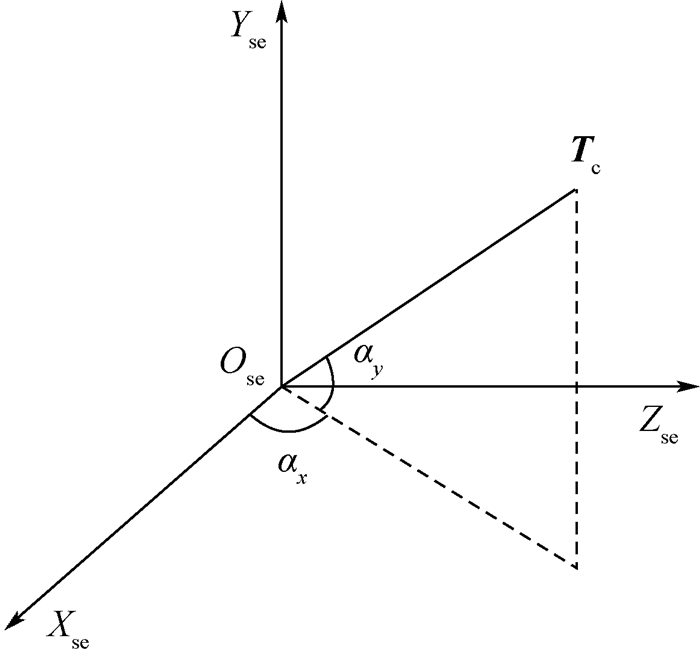
目标视线方向矢量示意图如图 2所示, Ose-XseYseZse为传感器坐标系。根据光轴的偏角,可计算得到由相机发出并最终到达目标的光线在传感器成像坐标系下的初始方向向量[7-8]Tc=(sin αxcos αy, sin αy, cos αxcos αy)。
|
| 图 2 目标视线方向矢量示意图 Fig. 2 Schematic diagram of target line-of-sight direction vector |
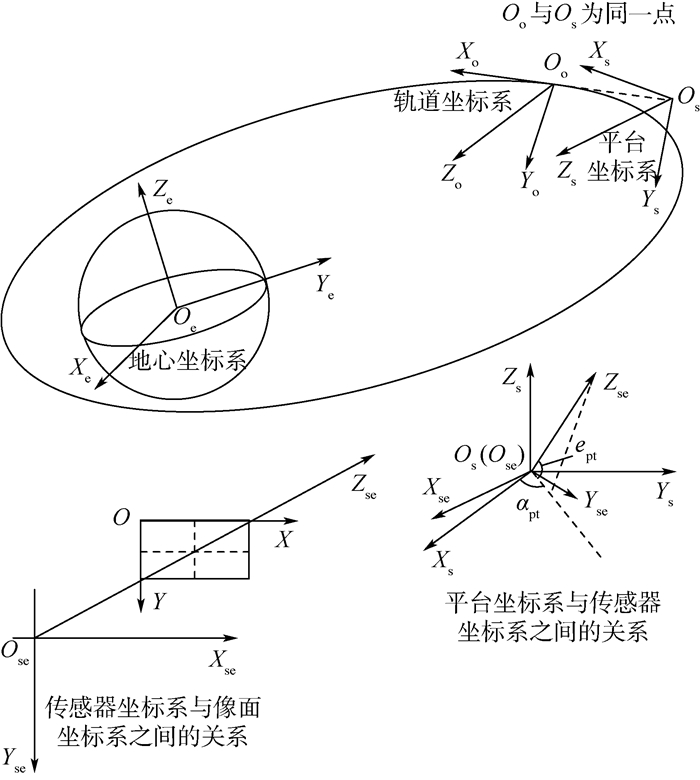
根据如图 3所示的成像投影相关坐标系的关系,可将先验获得的发射点位置及发射面转换到地心坐标系下,同时将目标视线矢量和发射面方程转换到统一的地心坐标系,坐标系变换涉及传感器坐标系、平台坐标系、轨道坐标系、地心坐标系等坐标系之间的转换[9-10]。
|
| 图 3 成像投影相关坐标系的关系示意图 Fig. 3 Schematic diagram of relationship between image projection related coordinate systems |
参见图 3,成像时刻tk时的坐标系转换矩阵为
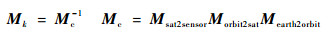
|
(1) |
式中:Mearth2orbit为地心坐标系Oe-XeYeZe到轨道坐标系Oo-XoYoZo的转换矩阵;Morbit2sat为轨道坐标系Oo-XoYoZo到平台坐标系Os-XsYsZs的转换矩阵;Msat2sensor为平台坐标系Os-XsYsZs到传感器坐标系Ose-XseYseZse的转换矩阵。图 3中的ept和αpt分别为传感器指向在Os-XsYsZs下的俯仰角和方位角。
根据目标视线方向及平台位置可得到过目标的射线方程为
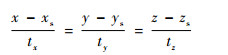
|
(2) |
式中:(xs, ys, zs)为传感器的空间位置;(tx, ty, tz)为射线的法向量;(x, y, z)为目标点P的空间位置, 可由以下联立方程解得
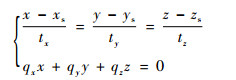
|
(3) |
式中:(qx, qy, qz)为平面法向量。
2 考虑大气折射影响的单平台目标空间位置反演由于受到地心引力的作用,地表大气密度分布不均。大量的实验研究表明,大气垂直方向比水平方向的变化要大1~3个数量级[11]。因此在实际研究大气折射对光线传播的影响时,常常忽略大气水平方向的变化,将大气视为水平方向均匀分布。将大气视为球面分层,每层大气均匀分布并且折射率相同,从而大气折射率可简化成仅随海拔高度h而变化的量,即N=N(h)[11-14]。
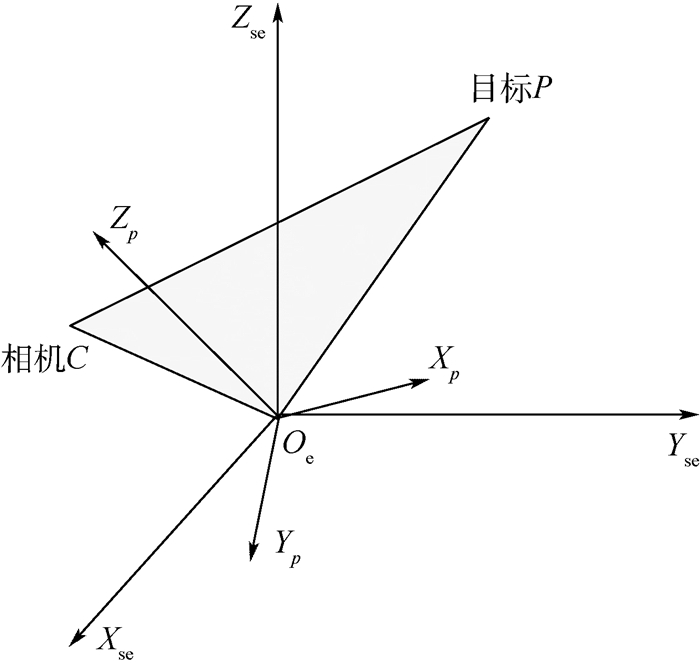
如图 4所示,设相机C在地心坐标系中坐标为(xc, yc, zc),目标P在地心坐标系中坐标为(xp, yp, zp),地心Oe坐标为(0, 0, 0)。相机、目标、地心3点组成的平面坐标系Oe-XpYpZp定义如下:平面坐标系的原点与地心直角坐标系的原点重合,平面OeCP与平面OeXeYe的交线OeXp为平面坐标系的Xp轴,Yp轴垂直平面OeCP,则由右手螺旋定则确定Zp轴。平面坐标系Oe-XpYpZp到地心坐标系Oe-XeYeZe的转换矩阵为
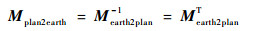
|
(4) |
|
| 图 4 地心坐标系与平面坐标系之间的关系图 Fig. 4 Relationship between geocentric coordinate system and plane coordinate system |
式中:Mearth2plan为地心坐标系Oe-XeYeZe到平面坐标系Oe-XpYpZp的转换矩阵。
为了方便计算光在每层中传输路径,相机、目标、地心平面内的点坐标和向量可转化到平面坐标系下,因为Yp轴坐标始终为0,所以将坐标记为二维平面坐标(xp, zp)的形式[15]。
将相机所在位置定义为第0层大气,相机的坐标作为第1层入射点位置,由目标点在相机C成像的图像上的位置P,得到相机发出并最终到达目标的光线的初始方向向量。相机发出并最终到达目标的光线的初始方向向量作为第1层入射方向,计算光在每层中折射传输路径,最终得到由相机C到目标的光线传输路径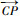
当光线由第i层射向第i+1层时,根据第i+1层入射角,第i层大气折射率,第i+1层大气折射率,计算第i+1层出射角。如图 5所示,当光线由第i层射向第i+1层时,第i+1层光线的入射方向向量vi+1,入射点坐标Ti+1=(xplan(i+1), zplan(i+1)),第i+1层入射角λi+1,第i层大气折射率ni,第i+1层大气折射率ni+1,每层的地心夹角dθ已知。光线在每层中传输路径的计算原理如下:

|
| 图 5 相机、目标和地心组成的平面内,光在每层大气中的传输路径图 Fig. 5 In plane composed of camera, target and center of the earth, transmission path of light in each layer of atmosphere |
根据大气球面分层Snell定律,由入射角λi+1、大气折射率ni、ni+1,求得第i+1层出射角φi+1。
大气折射率采用Hopfield模型进行计算,利用该模型可以求取任意海拔高度h的大气折射率n=N(h),Hopfield模型考虑了大气含有水汽的情况,将大气折射率分为干、湿2项[16-17]。
根据第i+1层入射点法线向量和出射角计算出射方向的单位向量。由第i+1层入射点法线向量Qi+1=[xplan(i+1), zplan(i+1)]和出射角φi+1,利用向量内积求得出射方向的单位向量ue=[ux, uz],具体求解方法为
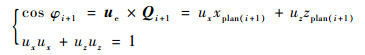
|
(5) |
根据第i+1层的地心夹角、出射角、其距地心的距离以及出射方向的单位向量,计算该层出射光线的长度,进而得到其出射光线方向向量,即第i+2层入射光线方向向量。在△OTi+1Ti+2中,根据正弦定理,利用公式:
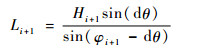
|
(6) |
求得第i+1层出射光线的长度Li+1,进而求得第i+1层出射光线方向向量Li+1ue,该方向向量即为第i+2层的入射光线方向向量vi+2,其中第i+1层的地心夹角为dθ、第i+1层距地心的距离为Hi+l。
由第i+1层入射点法线向量和第i+2层入射光线方向向量,计算得到第i+2层光线入射点法线向量。进而根据向量间的关系Qi+2-Qi+1=Li+1ue,求得第i+2层光线入射点Ti+2法线向量为
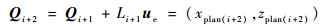
|
(7) |
根据第i+1层光线的入射点坐标和入射点向量计算第i+1层光线的交点;判断是否达到最后一层。在每层中求解射线与发射面的交点,已知发射点F(Xf, Yf, Zf)和发射面法向量fαj=[μαj, ναj, γαj],可使用点法式求解交点K(xk, yk, zk),当第i+1层光线的入射点Ti+1和第i+1层中交点Ki+l之间距离小于第i+1层光线的入射点Ti+1和第i+2层光线的入射点Ti+2之间距离时,交点Ki+l(xk, yk, zk)即为目标点。
3 目标运动参数估计求取所有序列图像上目标的实际空间位置pi(xo(i), yo(i), zo(i))并将得到的所有目标的空间位置作为轨迹点按顺序分成若干段,每段包括若干个轨迹点,分别对每段进行拟合计算,得到每段轨迹的加速度,进而计算整条轨迹的加速度变化平均值。
将序列图像得到的所有目标的空间位置作为轨迹点pk进行分段拟合,反演目标运动参数[18-20]。将轨迹点按顺序分成R段,每段轨迹点数为m,对于第l段的轨迹点pi, l(xo(i, l), yo(i, l), zo(i, l)), i=1, 2, …, m,一般情况下,目标在主动段和被动段的轨迹都可近似为抛物线,因此,采用二次多项式拟合模型更符合实际轨迹,可避免高阶多项式的过拟合情况。轨迹点坐标可由式(8)拟合:
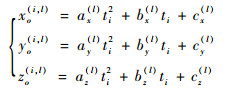
|
(8) |
式中:ax(l)、bx(l)和cx(l)为第l段x轴轨迹拟合二次多项式的系数,同理有y和z轴的系数。
对第l段轨迹中的m个点,采用最小二乘法可求解得到拟合系数,则第l段的i帧目标速度Vi(l)(vi, x(l), vi, y(l), vi, z(l))为
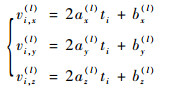
|
(9) |
第l段轨迹的加速度为a(l)(ax(l), ay(l), az(l)),整条轨迹的加速度变化的平均值
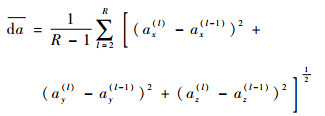
|
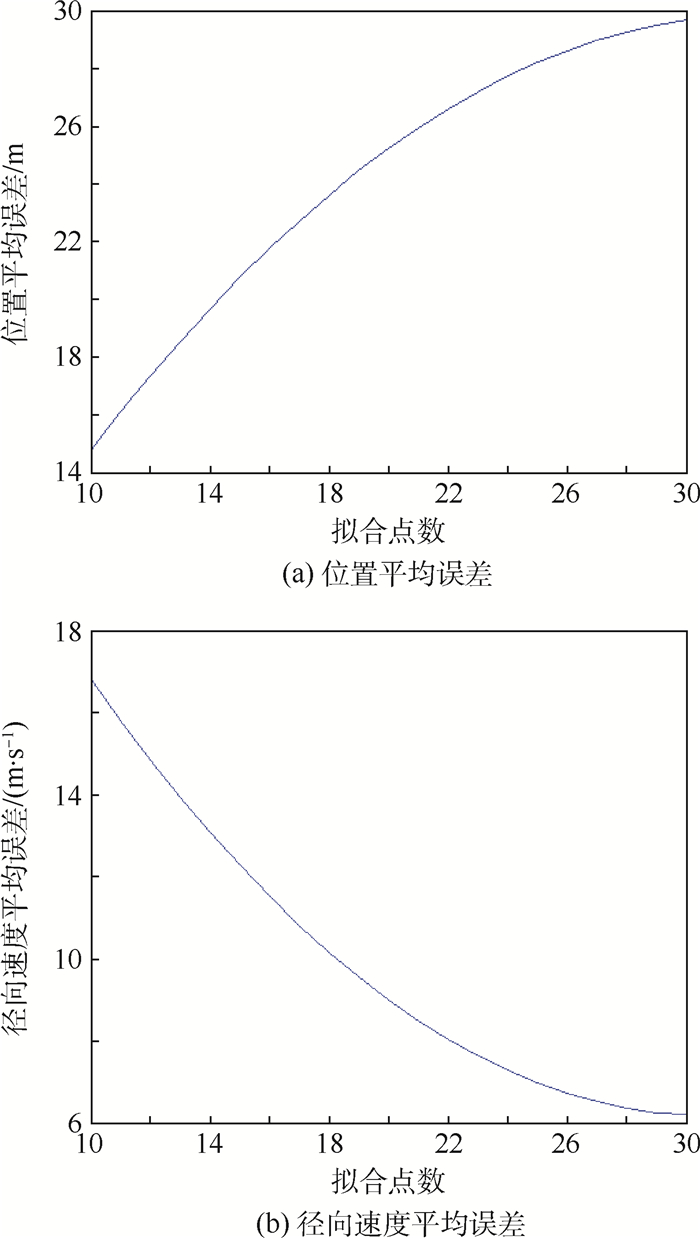
在用二阶多项式拟合时,为了保证足够高的拟合精度,采用分段拟合的方式来减小拟合误差。图 6为对实际轨迹采用上述拟合方式时,位置平均误差和径向速度平均误差曲线。
|
| 图 6 位置及径向速度平均误差随拟合点数变化曲线 Fig. 6 Curves of location and radial velocity average error changing with number of fitting points |
考虑到实际检测数据点数,仅仅比对两者拟合点数在10~30范围内的情况。可以看出,在拟合点数为10~30范围内,位置平均误差随拟合点数增加而增加,而径向速度平均误差随拟合点数增加而减小。发生上述情况的原因是拟合时3个分量各自分别拟合,而实际中轨迹的3个分量存在一定的耦合,随着点数增多位置拟合误差会增大,而拟合点数增多时拟合出的曲线形状与实际更相似,所以速度误差会降低。取折中的情况,采用拟合点数为20的分段拟合。
4 估计参数的迭代优化先验给出的发射面参数经常存在误差,且该误差对重建精度有极大影响,因此需要在重建过程中同时优化发射面参数,以提高重建精度。目标运动在短时间内可近似为匀加速直线运动,发射面准确时即理想情况下,所重建的运动加速度应为一常量。若发射面参数不准确即发射面发生偏转,目标将变为变加速运动。故在对重建目标点进行分段拟合时,理论上每一段的加速度较之于前一段的加速度差值其绝对值和应接近于零,而对于变加速运动,发射面偏转越大,差值越大。
预先设定一组发射面偏角,并设置初始的发射点位置和发射面法向量,j=0。给定一组发射面偏角αj,αj=-β+jdβ,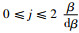
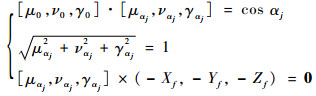
|
(10) |
对应于发射面偏角αj,可反演出相应的目标运动参数(x, y, z, v, a, da)aj,分别为位置坐标(x, y, z),速度v,加速度a和加速度差da,则最优目标运动参数为
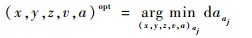
|
(11) |
图 7为发射点经纬高为(E97.306°, N41.090°, 6 369.853 km),发射面法向量为(-0.137, 0.604, 0.784)的轨迹在不同偏角情况下的反演加速度差值和的变化曲线,记录加速度变化平均值的最小值以及相对应的发射面偏角、发射点位置、发射面法向量。将此条件下得到的轨迹点作为最后的反演轨迹。

|
| 图 7 发射面优化分析图 Fig. 7 Diagram of launch plane optimization analysis |
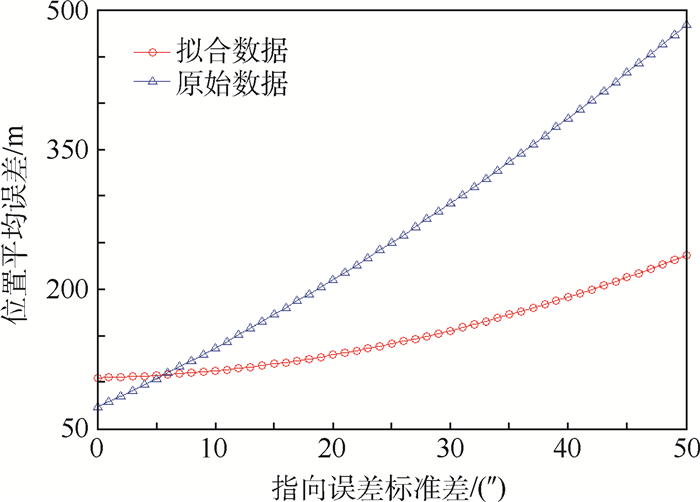
在发射点和发射面等先验信息准确情形下,不考虑成像和检测的影响因素,单平台定位的位置平均误差标准差和径向速度平均误差与指向误差标准差的关系如图 8、图 9所示。
|
| 图 8 单平台定位的位置平均误差随指向误差标准差变化曲线 Fig. 8 Curves of single platform positioning's location average error changing with pointing error standard deviation |

|
| 图 9 单平台定位的径向速度平均误差随指向误差标准差变化曲线 Fig. 9 Curve of single platform positioning's radial velocity average error changing with pointing error standard deviation |
从图 8可以看出,单平台定位时,分段拟合的方法在指向误差极小的情形下会带来误差增大,但是指向误差标准差在5″内时能够有效地抑制指向误差引起的定位误差,并且误差在500 m以下,有足够空间考虑成像和检测的误差。图 9显示指向误差标准差变化范围为(0″, 50″)时,径向速度平均误差与指向误差的标准差成正相关,径向速度平均误差小于60 m/s。
由单平台下检测到的目标像面位置重建三维轨迹是典型的病态问题,先验知识发射点位置和发射面指向显的尤为重要,其中发射点位置能够精确获得,故发射面指向是影响单平台定位误差的关键因素。
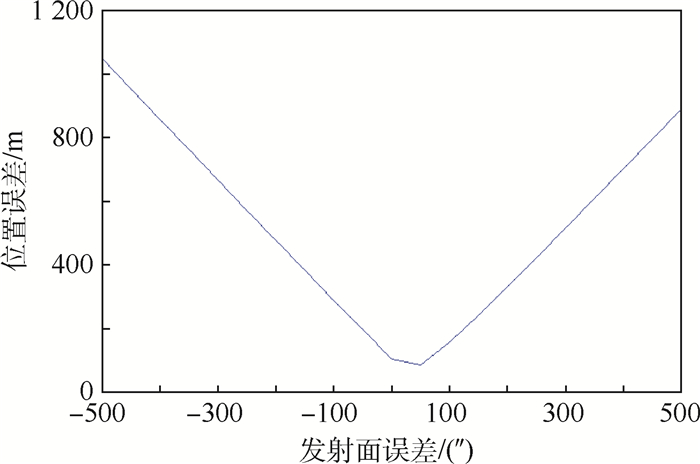
从图 10可以看出, 即使是根据已知的准确轨迹拟合出来的发射面都不是十分准确,而在实际目标飞行过程中,受到环境影响因素太多,发射面不能保持准确,并会产生很大的误差。从图中可以看出在发射面偏转500″,也就是0.139°,在实际中可看做是较小的误差,但是目标重建位置误差已经在1 km以上。故单平台定位在实际应用中存在很大的难题也就是发射面准确度的问题,其定位误差远大于双平台定位误差。
|
| 图 10 单平台定位的位置误差随发射面误差变化曲线 Fig. 10 Curve of single platform positioning's locationerror changing with launch plane error |
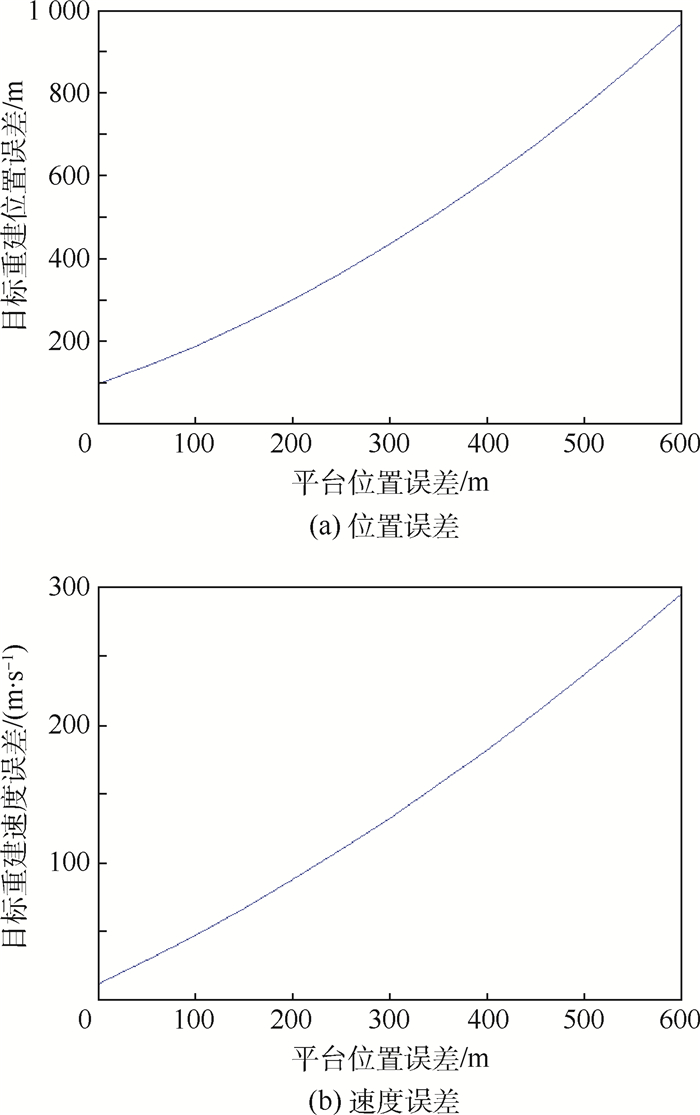
在空间目标点位置确定的情况下,影响定位精度的另一个重要因素就是平台位置误差,在高空中平台位置的变化给定位带来很大的影响,分别对平台位置误差添加均值为0,不同标准差的随机误差,统计分析平台位置误差给定位精度带来的影响,图 11为平台位置误差给目标重建位置和速度带来的误差。
|
| 图 11 平台位置误差对目标重建位置误差及速度误差的影响 Fig. 11 Effect of platform location error on target reconstruction location error and speed error |
从图 11可以看出平台位置相较于其他影响因素,对目标重建速度误差带来的误差影响是很大的。在平台位置误差为420 m时,重建速度误差已经比较大,而重建位置误差符合定位要求。
综上实验,主要分析了对单平台成像目标运动特性反演误差影响因素,包括平台指向误差、平台位置误差、发射面偏转误差和分段拟合点数。在上述影响因素取误差范围最大值时,综合误差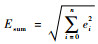
本文针对单平台下的观测数据进行空间轨迹重建是典型的病态问题,提出单平台成像目标运动特性反演方法,得到:
1) 本文提出从平台位置出发,反向追踪,将大气划分多层,计算在大气传输路径,最终与发射面相交得到目标位置,并通过迭代优化发射面和分段拟合等方法抑制重建误差,此方法能够有效反演单平台目标运动特性。
2) 通过本文提出的单平台目标运动特性反演方法,目标反演位置误差在200 m以下,速度误差在60 m/s以下,能够用作实际场景。
3) 对重建出的原始数据进行分段拟合,能够有效的抑制重建的位置误差及速度误差。
4) 在各影响因素中,发射面的精确度的影响最大,较小的偏转就会带来很大的反演误差,而通过发射面的迭代优化,可以较为有效地抑制小范围发射面的偏转带来误差。
| [1] |
魏晨曦, 马婷婷. 美国未来的侦察卫星及其关键技术[J]. 国际太空, 2005(3): 23-24. WEI C X, MA T T. The future reconnaissance satellite of the United States and the key technologies[J]. International Space, 2005(3): 23-24. (in Chinese) |
| [2] |
张天序. 成像自动目标识别[M]. 武汉: 湖北科学技术出版社, 2005: 19-40. ZHANG T X. Imaging automatic target recognition[M]. Wuhan: Hubei Science and Technology Press, 2005: 19-40. (in Chinese) |
| [3] |
DANIS N J. Space-based tactical ballistic missile launch parameter estimation[J]. IEEE Transactions on Aerospace and Electronic Systems, 1993, 29(2): 412-424. DOI:10.1109/7.210079 |
| [4] |
李英良.单星弹道估计与预报中的方法研究[D].长沙: 国防科技大学, 2004. LI Y L.Research on method of single star ballistic estimation and forecast[D].Changsha: National University of Defense Technology, 2004(in Chinese). |
| [5] |
SITZMAN G L, DRESCHER G H.Tactical ballistic missile trajectory state and error covariance propagation[C]//IEEE Position Location and Navigation Symposium.Piscataway, NJ: IEEE Press, 1994: 839-844.
|
| [6] |
申镇.单星预警弹道导弹参数估计方法研究[D].长沙: 国防科技大学, 2010. SHEN Z.The single satellite early warning ballistic missile parameter estimation research[D].Changsha: National University of Defense Technology, 2010(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-90002-2010271158.htm |
| [7] |
阮晓东, 李世伦, 诸葛良, 等. 用立体视觉测量多自由度机械装置姿态的研究[J]. 中国机械工程, 2000, 11(5): 571-573. RUAN X D, LI S L, ZHUGE L, et al. Research on measuring the attitude of multi-degree-of-freedom mechanism with stereo vision[J]. Chinese Journal of Mechanical Engineering, 2000, 11(5): 571-573. DOI:10.3321/j.issn:1004-132X.2000.05.028 (in Chinese) |
| [8] |
罗世民, 李茂西. 双目视觉测量中三维坐标的求取方法研究[J]. 计算机工程与设计, 2006, 27(19): 3622-3624. LUO S M, LI M X. Research on the method of calculating three-dimensional coordinates in binocular vision measurement[J]. Computer Engineering and Design, 2006, 27(19): 3622-3624. DOI:10.3969/j.issn.1000-7024.2006.19.037 (in Chinese) |
| [9] |
ZHANG K, XU B, TANG L X, et al. Modeling of binocular vision system for 3D reconstruction with improved genetic algorithms[J]. The International Journal of Advanced Manufacturing Technology, 2006, 29(7): 722-728. |
| [10] |
HEIKKILA J. Geometric camera calibration using circular control points[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 22(10): 1066-1077. DOI:10.1109/34.879788 |
| [11] |
ZHAO Q Y, HAACK T, ROGERS T, et al. Ensemble prediction of atmospheric refractivity conditions for EM propagation[J]. Journal of Applied Meteorology and Climatology, 2016, 55(10): 2113-2130. DOI:10.1175/JAMC-D-16-0033.1 |
| [12] |
严豪健. 大气折射的研究进展[J]. 世界科技研究进展, 2006, 28(1): 48-58. YAN H J. Research progress of atmospheric refraction[J]. World Science and Technology Research Progress, 2006, 28(1): 48-58. (in Chinese) |
| [13] |
SMITH E K, WEINTRAUB S. The constants in the equation for atmospheric refractive index at radio frequencies[J]. Proceedings of the IRE, 1953, 41(8): 1035-1037. DOI:10.1109/JRPROC.1953.274297 |
| [14] |
GUO X, KANG S, ZHANG Y.A simple method to estimate clear air refractivity profile in the stably stratified marine atmospheric boundary layer[C]//2014 XXXIth URSI General Assembly and Scientific Symposium (URSI GASS).Piscataway, NJ: IEEE Press, 2014: 1-4.
|
| [15] |
于丽娟.新型弱目标检测及目标空间定位算法研究[D].武汉: 华中科技大学, 2016. YU L J.New weak target detection and target space locating algorithm[D].Wuhan: Huazhong University of Science and Technology, 2016(in Chinese). |
| [16] |
GRABNER M, KVICERA V, PECHAC P, et al. World maps of atmospheric refractivity statistics[J]. IEEE Transactions on Antennas and Propagation, 2014, 62(7): 3714-3722. DOI:10.1109/TAP.2014.2317474 |
| [17] |
陈祥明.大气折射率剖面模型与电波折射误差修正方法研究[D].青岛: 中国海洋大学, 2008: 8-10. CHEN X M.Study on atmospheric refractivity profile model and radio wave refraction error correction method[D].Qingdao: Ocean University of China, 2008: 8-10(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10423-2008175945.htm |
| [18] |
杨剑, 吕乃光, 董明利. 加权最小二乘算法在机器视觉系统中的应用[J]. 光学精密工程, 2009, 17(8): 1870-1877. YANG J, LÜ N G, DONG M L. The application of weighted least squares algorithm in machine vision system[J]. Optical Precision Engineering, 2009, 17(8): 1870-1877. DOI:10.3321/j.issn:1004-924X.2009.08.014 (in Chinese) |
| [19] |
KANAYET F J, MATTARELLA-MICKE A, KOHLER P J, et al. Distinct representations of magnitude and spatial position within parietal cortex during number-Space mapping[J]. Journal of Cognitive Neuroscience, 2018, 30(2): 200-218. DOI:10.1162/jocn_a_01199 |
| [20] |
KIM H S, HWANG D Y, KIM K H, et al.Reducing positioning errors in the important access point selection method for fingerprint localization by spatial partitioning[C]//2017 International Conference on Information Networking.Piscataway, NJ: IEEE Press, 2017: 445-447.
|



