Lambert问题是航天工程中双脉冲轨道转移的基本问题[1-3],在航天器交会领域有广泛的应用,近年来仍然属于热点研究范畴[4-7]。
Lambert飞行时间定理指出,对同一个平方反比中心引力场的椭圆轨道转移问题,给定转移前后的空间位置P1和P2,则转移时间t2-t1仅依赖于轨道半长轴aT,两点离引力中心F的矢径长度之和r1+r2以及连接两点的弦长cT。如果这3个参数aT、r1+r2、cT给定,则转移时间t2-t1是确定的,单圈Lambert转移情况下通常是2个解(最小能量轨道时是一个解),与转移椭圆的形状(偏心率eT)无关[8]。基于飞行时间定理,基本Lambert问题是指给定轨道上两点的位置矢量及飞行时间,求连接两点的轨道参数。基本Lambert问题是一个典型的双脉冲变轨问题,其本质是求解微分方程两点边值问题[9]。
航天工程中通常需要根据优化指标确定转移轨道的变轨优化问题。常用的优化指标是时间最优或燃料最优。基本Lambert问题的结论可用于直接求解时间最优双脉冲变轨问题[10]。很多任务中需要针对燃料消耗或者能量变化提出优化目标要求,并不限制转移时间。此时最优转移轨道是满足两点约束的不同半通径对应的一系列转移轨道中的一个最优解。这个问题称为能量最优和燃料最优Lambert问题。
文献[11]对目前飞行器轨迹优化数值方法进行总结整理和归纳。文献[12]对能量最优Lambert进行详细研究并给出该问题的解析闭式解答。文献[13]用优化方法证明了Lambert变轨的最小能量轨道问题。文献[14]研究了共面椭圆轨道间转移的燃料最优Lambert问题。文献[15]研究了最优双冲量交会问题的一般数学模型和数值求解方法。文献[16]综述了当前最优冲量交会的研究进展。文献[17]给出一种最优Lambert转移时间燃料多目标混合模型并采用混合遗传算法求解。
在对上述文献深入研究的基础上,本文提出一种基于矢量形式的求解能量最优和燃料最优Lambert问题的总体框架,把文献[12, 14]的求解过程统一在本文提出的数学框架中,并给出了能量最优和燃料最优Lambert问题的解析计算方法。最后分析和对比了能量最优和燃料最优Lambert问题求解过程的多项式方程相应的性质和特点。
1 能量最优与燃料最优Lambert问题的定义能量最优和燃料最优Lambert问题具体描述如下(文中涉及的位置和速度向量都是三维列向量)。
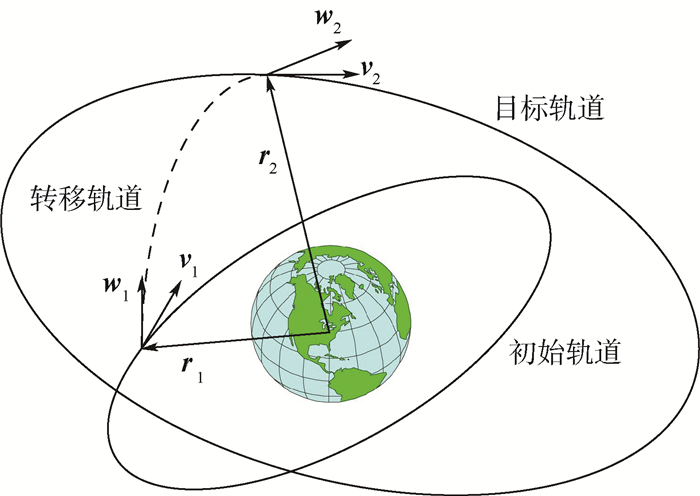
如图 1所示,设航天器变轨前的位置为r1和速度v1, 变轨后的位置r2和速度v2,求解航天器在r1、r2处的速度w1、w2,计算航天器2次点火的速度增量Δv1和Δv2:
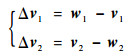
|
(1) |
|
| 图 1 位置和速度向量定义 Fig. 1 Definition of location and velocity vectors |
当优化目标函数为
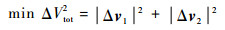
|
(2) |
此类问题称为ΔV2 Lambert问题,或能量最优Lambert问题。
当优化目标函数为
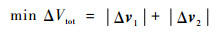
|
(3) |
此类问题称为ΔV Lambert问题,或燃料最优Lambert问题。
事实上ΔV Lambert问题的本质体现了燃料最优。而以ΔVtot2为目标函数的ΔV2 Lambert问题是一个能量最优问题,并非燃料最优。ΔV2 Lambert问题所计算的燃料消耗大于等于ΔV2 Lambert问题,证明如下[12]:
假设m是ΔV Lambert问题求得的最优解,q是ΔV2 Lambert问题求得的最优解,即ΔVtot(m)≤ΔVtot(q),ΔVtot2(q)≤ΔVtot2(m)。根据不等式关系:|x|+|y|≤ 
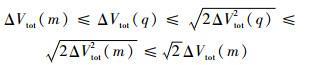
|
(4) |
式(4)意味着ΔV2最优轨道的燃料消耗大于等于ΔV最优轨道的燃料消耗,上限为不多于ΔV Lambert问题燃料消耗的41.5%。实际中通常二者燃料消耗差值不大于17%。圆轨道霍曼转移情况下二者相等。
2 能量最优和燃料最优Lambert问题的计算变轨起始点和终止点的速度w1和w2满足[13]:
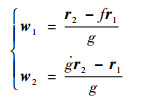
|
(5) |
式中:
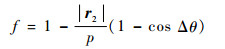
|
(6) |
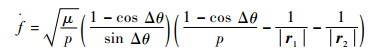
|
(7) |
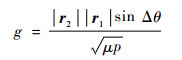
|
(8) |
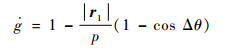
|
(9) |
其中:μ为引力常数;Δθ为r1、r2处的真近点角差值;p为转移轨道半通径。
2.1 ΔV2 Lambert问题的求解对于ΔV2 Lambert问题,求转移能量最小即求式(10)的最小值:
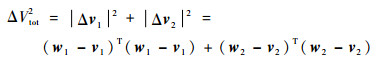
|
(10) |
式(10)取最小值需要满足条件:
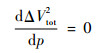
|
(11) |
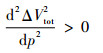
|
(12) |
求解式(11)和式(12)即可得到满足条件的p值,从而确定最优转移轨道和2次冲量的值。
2.2 ΔV Lambert问题的求解对于ΔV Lambert问题,求性能函数最小即求解式(13)的最小值:
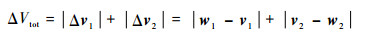
|
(13) |
求式(13)最小值需要满足条件: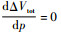
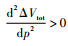
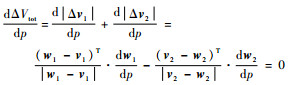
|
(14) |
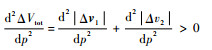
|
(15) |
式中:
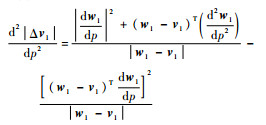
|
(16) |

|
(17) |
ΔV和ΔV2 Lambert问题的求解中都涉及到变轨起始点和终止点的速度w1和w2相对于半通径p的一阶和二阶导数。为计算方便,令
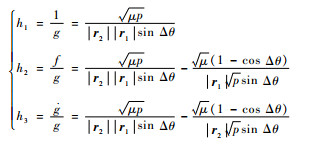
|
(18) |
再令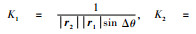
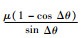
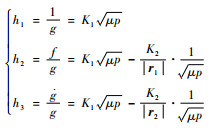
|
(19) |
从而得
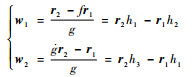
|
(20) |
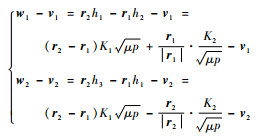
|
(21) |
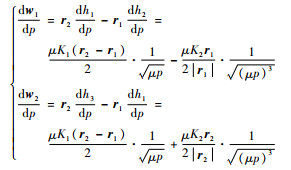
|
(22) |
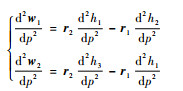
|
(23) |
将式(20)~式(23)代入式(11)和式(12)、式(14)和式(15),即可通过求解方程得到ΔV和ΔV2 Lambert问题对应的p值,继而求出ΔVtot和ΔVtot2以及2次速度增量的值。
2.4 求解导数方程的相关结论结论1 ΔV2 Lambert问题(10)归结为一个四次多项式方程求解问题。
式(10)展开为
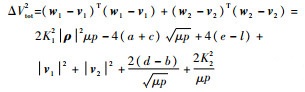
|
(24) |
式中: 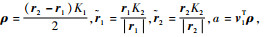
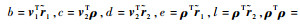
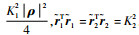
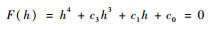
|
(25) |
式中: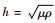
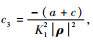

结论2 ΔV Lambert问题(13)归结为一个八次多项式方程求解问题。
式(14)可写为
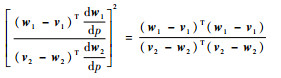
|
(26) |
将式(21)、式(22)代入式(26)会得到一个形如式(27)的多项式方程:
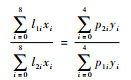
|
(27) |
式中:xi=h-i,yi=h2-i,l1i、l2i、p1i、p2i为计算出的多项式系数。式(27)形式上为一个12阶多项式方程,但实际上式(27)中hi项中i=2, 1, -9, -10的系数为零,为一个八次多项式方程:
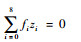
|
(28) |
其中:zi=h-i,fi取值为
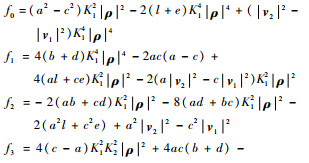
|
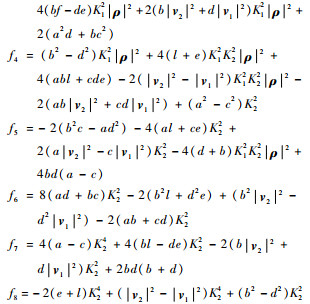
|
这个八次多项式方程式(28)通常没有求根公式,需采用数值法求解。
综上所述,以min ΔVtot为目标函数的ΔV Lambert问题涉及到八次多项式求根问题,目前尚无闭式解析解,数值解往往受到迭代算法的速度影响。而求解ΔV2 Lambert问题涉及缺项的四次多项式求根问题,存在闭式解求根公式。
3 仿真算例仿真算例采用文献[12]的ALSET 1和ARIANE 44L卫星的轨道参数,列于表 1。
| ALSET 1 | ||||||||
| 1 | 27 559U | 02 054A | 08 259.526 859 48 | -0.000 000 02 | 00 000-0 | 84 653-5 | 0 | 6 025 |
| 2 | 27 559 | 097.980 7 | 137.478 4 | 0 009 664 | 216.549 4 | 143.504 7 | 14.629 778 973 095 34 | |
| ARIANE 44L | ||||||||
| 1 | 28 576U | 91 075N | 08 351.945 684 14 | 0.000 001 79 | 00 000-0 | 64 019-2 | 0 | 6 927 |
| 2 | 28 576 | 006.553 4 | 128.062 9 | 6 595 687 | 237.361 1 | 042.002 9 | 02.835 874 63 | 72 170 |
| km | |||
| 位置 | rx | ry | rz |
| r1 | 3 160.125 4 | -3 850.670 7 | -5 011.985 2 |
| r2 | -16 875.892 6 | 14 279.183 4 | 516.039 2 |
| km/s | |||
| 速度 | vx | vy | vz |
| v1 | -4.458 | 3.101 2 | -5.191 6 |
| v2 | -1.276 5 | 1.799 5 | 3.043 9 |
| km/s | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 速度增量 | Δwx | Δwy | Δwz | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Δw1 | -1.361 22 | 0.147 84 | -1.625 77 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Δw2 | 8.786×10-6 | 8.841×10-6 | 10.017×10-6 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| km/s | |||
| 速度增量 | Δwx | Δwy | Δwz |
| Δw1 | -1.300 08 | 0.085 91 | -1.670 27 |
| Δw2 | -0.076 03 | 0.066 70 | 0.012 16 |
| 目标函数 | p/km | 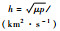 |
目标函数值/ (km·s-1) |
| ΔVtot | 11 360.100 | 67 291.462 | 2.125 56 |
| ΔVtot2 | 11 285.930 | 67 071.429 | 4.497 8 |
对于ΔV Lambert问题的最小速度增量值,若利用ΔV2 Lambert问题求解得到的p值(设q=11 285.930)计算,相比ΔV Lambert问题求解得到的p值(设m=11 360.100),有ΔVtot(q)-ΔVtot(m)=0.094 669 588 639 047,ΔVtot(q)高出ΔVtot(m)4.453 9%。
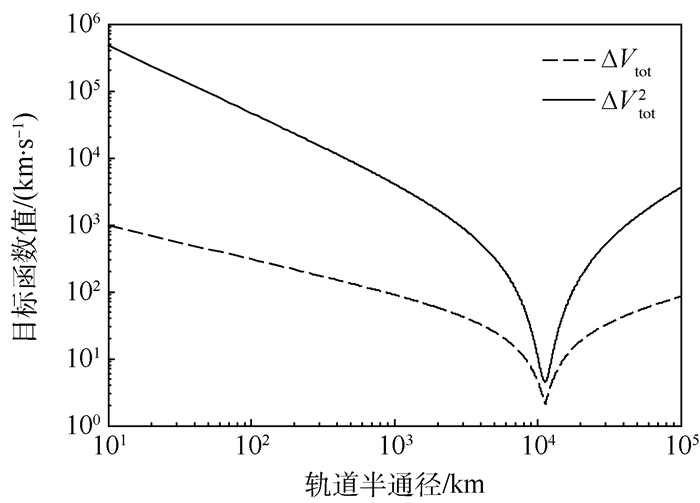
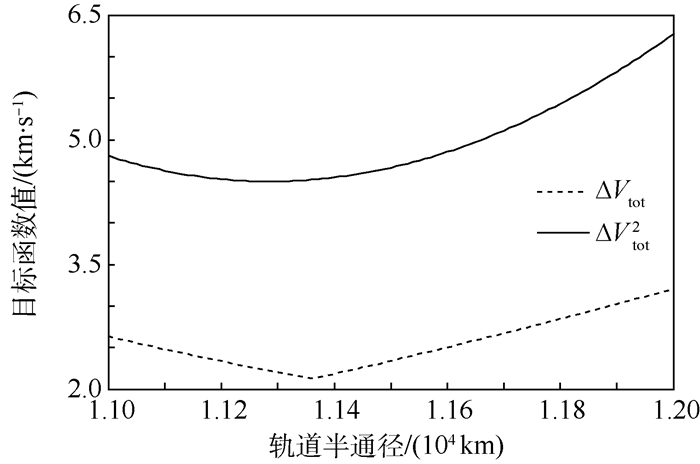
ΔV和ΔV2目标函数值随p变化情况如图 2所示(对数坐标),局部细节情况见图 3。极值点和表 4~表 6计算结果一致。
|
| 图 2 ΔVtot和ΔVtot2目标函数值随p变化情况 Fig. 2 Variation of ΔVtot and ΔVtot2 function with p |
|
| 图 3 ΔVtot和ΔVtot2目标函数值随p变化情况(极点附近) Fig. 3 Variation of ΔVtot and ΔVtot2 function with p (near peak point) |
1) 本文提出一种基于矢量形式的求解能量最优和燃料最优Lambert问题的总体框架,统一了能量最优和燃料最优Lambert问题的分析方法和相关结论,避免了大量三角函数运算和坐标变换等较繁琐的处理方式。
2) 对燃料最优Lambert问题的分析突破了相关研究中轨道共面条件的限制。本文的推导过程相比以往的研究具有更加简洁的表示形式。
3) 仿真算例展示了具体方法的求解结果,并验证了燃料最优比能量最优的最优速度增量多不超过17%的事实。
| [1] | AVANZIA G. A simple Lambert algorithm[J]. Journal of Guidance, Control, and Dynamics, 2008, 31 (2): 1587–1594. |
| [2] | BATTIN R H. Lambert's problem revisited[J]. AIAA Journal, 1977, 15 (5): 705–713. |
| [3] | BLANCHARD R C, DEVANEY R A, LANCASTER E R. A note on Lambert's theorem[J]. Journal of Spacecraft and Rockets, 1966, 3 (9): 1436–1438. DOI:10.2514/3.28673 |
| [4] | AVANZINI G, PALMAS A, VELLUTINI E. Solution of low-thrust Lambert problem with perturbative expansions of equinoctial elements[J]. Journal of Guidance, Control, and Dynamics, 2015, 38 (8): 1585–1601. |
| [5] | SCHUMACHERJR P W, SABOL C, HIGGINSON C, et al. Uncertain Lambert problem[J]. Journal of Guidance, Control, and Dynamics, 2015, 38 (7): 1573–1584. |
| [6] | WEN C, ZHAO Y, SHI P. Derivative analysis and algorithm modification of transverse-eccentricity-based Lambert problem[J]. Journal of Guidance, Control, and Dynamics, 2014, 37 (4): 1195–1201. DOI:10.2514/1.62351 |
| [7] | ZHANG G, MORTARI D, ZHOU D. Constrained multiple-revolution Lambert's problem[J]. Journal of Guidance, Control, and Dynamics, 2010, 33 (4): 1779–1786. |
| [8] |
朱仁璋.
航天器交会对接技术[M]. 北京: 国防工业出版社, 2007: 37.
ZHU R Z. Rendezvous and docking techniques of spacecraft[M]. Beijing: National Defense Industry Press, 2007: 37. (in Chinese) |
| [9] |
唐国金.
航天器轨迹优化理论、方法及应用[M]. 北京: 科学出版社, 2012: 178.
TANG G J. Spacecraft trajectory optimization theory, method and application[M]. Beijing: Science Press, 2012: 178. (in Chinese) |
| [10] |
朱仁璋, 蒙薇, 胡锡婷. 航天器交会中的Lambert问题[J].
中国空间科学技术, 2006, 26 (1): 49–55.
ZHU R Z, MENG W, HU X T. Lambert problem in spacecraft rendezvous[J]. Chinese Space Science and Technology, 2006, 26 (1): 49–55. (in Chinese) |
| [11] |
雍恩米, 陈磊, 唐国金. 飞行器轨迹优化数值方法综述[J].
宇航学报, 2008, 29 (3): 397–406.
YONG E M, CHEN L, TANG G J. A survey of numerical methods for trajectory optimization of spacecraft[J]. Journal of Astronautics, 2008, 29 (3): 397–406. (in Chinese) |
| [12] | AVENDANO M, MORTARI D. A closed-form solution to the minimum ΔVtot2 Lambert's problem[J]. Celestial Mechanics & Dynamical Astronomy, 2010, 106 (1): 25–37. |
| [13] | LEEGHIM H, JAROUX B A. Energy-optimal solution to the Lambert problem[J]. Journal of Guidance, Control, and Dynamics, 2010, 33 (1): 1008–1010. |
| [14] | PRADO A F, BROUCKE A R. The minimum delta-V Lambert's problem[J]. Control and Automation, 1996, 2 (1): 84–90. |
| [15] |
佘志坤, 薛白, 丛源良, 等. 最优双冲量交会问题的数学建模与数值求解[J].
宇航学报, 2010, 31 (1): 155–161.
SHE Z K, XUE B, CONG Y L, et al. Mathematical modeling and numerical solving of the optimal two-impulse rendezvous problem[J]. Journal of Astronautics, 2010, 31 (1): 155–161. DOI:10.3873/j.issn.1000-1328.2010.01.025 (in Chinese) |
| [16] |
陈长青, 解永春. 最优冲量交会的研究进展[J].
空间控制技术与应用, 2008, 34 (12): 18–23.
CHEN C Q, XIE Y C. Development of optimal impulsive rendezvous[J]. Aerospace Control and Application, 2008, 34 (12): 18–23. (in Chinese) |
| [17] |
黄勇, 李小将, 张东来, 等. 混合遗传算法在最优Lambert轨道转移设计中的应用[J].
飞行力学, 2013, 31 (3): 269–272.
HUANG Y, LI X J, ZHANG D L, et al. Application of hybrid genetic algorithm in optimal Lambert orbital transfer design[J]. Flight Dynamics, 2013, 31 (3): 269–272. (in Chinese) |



