各种高新技术在军事领域的大量应用使得航空装备呈现出多层次结构、多功能属性、多域分布的特点,同时为航空装备的安全管理提出了极大的挑战[1]。部队装备现代化水平逐年提升,装备的使用条件复杂多变,各种风险因素之间相互影响,系统内外环境间的平衡状态一旦被打破,就会发生事故。多风险因素间的风险传导对装备完好性和作战效能的提高影响很大,对于复杂装备风险传导的研究已经成为复杂装备安全性分析的关键环节[2-3]。
当前,针对复杂装备风险传导的研究不多。文献[4]将影响复杂装备安全性的风险因素称为风险元;文献[5]研究发现风险元间存在传导的现象;文献[6]改进区域安全分析法,从定性角度分析了风险元间的传导;文献[7-8]从定量角度分析风险元间的传导,但只考虑了充足样本条件下可以得到概率分布的情况,未考虑其他非决定现象;文献[9]构建复杂武器装备网络化制造模型,利用模糊评判,其风险传导过程刻画不够清晰,效果不够理想,需要更完备的工具进行分析。
图形评审技术(Gragh Evaluation Review Technique, GERT)是在系统外部非决定性条件和系统内部非决定性因素共同影响下对系统的活动过程进行的网络分析技术[10]。文献[11]虽然基于GERT模型可以对复杂装备的安全性进行有效分析,但是GERT模型只描述了随机现象,即模型参数只包括实现概率和随机变量的概率分布。但是在实际复杂的生活中,非决定性条件和因素有些表现为随机性,有些表现为不确定性[12]。只存在随机变量时,应用概率论解决问题;只存在不确定变量时,应用不确定理论分析问题[13];如果同时存在随机变量和不确定变量,利用机会理论处理这种混合的非决定问题[14-15]。本文尝试利用机会理论改进GERT模型,同时考虑多种风险因素的影响,提出不确定随机多传递参量GERT(Uncertain Random Multi-Transfer Parameter GERT,UR-MTPGERT)。
本文在GERT模型和机会理论的基础上,提出了UR-MTPGERT网络模型。针对传统GERT模型只能得到系统风险度,不能分析微观信息的缺陷,通过风险元重要度和风险路径关联度对模型进行扩展分析。应用德尔菲法求解不确定变量的不确定分布,应用极大熵[16-17]模型求解任意随机变量的概率密度函数,应用矩阵分析计算网络参数,定量分析复杂装备风险传导过程,以进一步揭示复杂装备的风险演化机理。
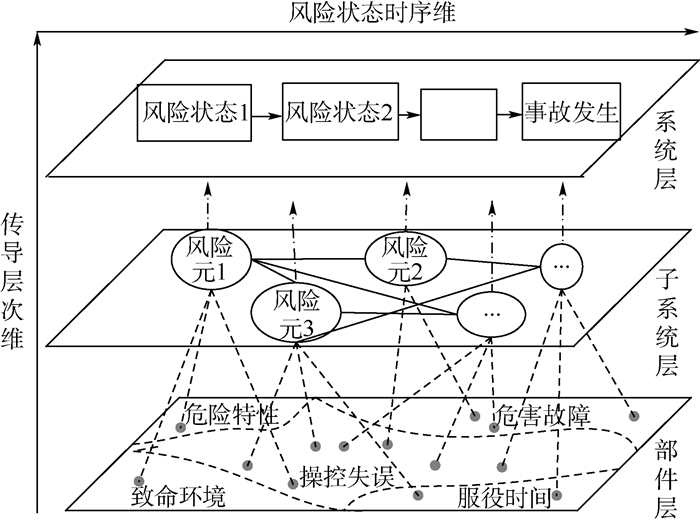
1 风险传导UR-MTPGERT网络模型按照佩罗[2]提出的事故分层思想,可以将事故层次划分为部件层、子系统层和系统层,构建装备服役风险传导网络模型如图 1所示。第1层为部件层,可以通过各种事故致因模型分析得到,在此基础上运用历史数据、专家经验或仿真的方式对风险因素进行评价。第2层为子系统层,每个子系统可以视为一个风险元,风险元包含的风险因素的风险度由第1层获得。第3层为系统层,风险元之间的相互影响在一段时间内呈现出不同的演化状态,构成系统的风险演化轨迹。复杂装备事故突变在该层次被看作是各子系统风险状态的时序变化过程。在此基础上分析各个子系统的风险度变化趋势,最终得到复杂装备的总体风险度。
|
| 图 1 装备服役风险传导网络模型 Fig. 1 Equipment service risk conduction network model |
复杂装备风险传导的总体风险度利用UR-MTPGERT网络模型求出。如果将复杂装备中的风险元视作网络的节点,将风险元间的相互影响关系视作网络的边,将风险度hi、风险传导强度pij视为网络的流,可以建立复杂装备风险传导UR-MTPGERT基本单元结构模型如图 2所示。

|
| 图 2 风险传导UR-MTPGERT基本单元构成示意图 Fig. 2 Schematic of basic unit structure of risk conduction UR-MTPGERT |
定义1 设U={u1, u2, …, un}为只含有“异或”型风险元的节点集合;A={ai|ai=(ui, uj)}为风险元节点的连接枝线的集合;S=(U×A)∪(A×U)={sij|(P, H)}为风险元节点的连接枝线ai上的风险流集合,P={pij|U×A→(0, 1)}为风险元风险传导强度的集合,H={hi(hi1, hi2, …, hin)|U×A→H}为节点风险度的集合。那么称三元组Z=(U, A, S)为复杂装备风险传导UR-MTPGERT网络模型。
1.2 构造矩母函数定义2 设hi∈R为复杂装备风险元ui的风险度,则称
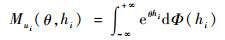
|
(1) |
为风险元ui风险度hi的矩母函数;称

|
(2) |
为边ui→uj的传递系数。
为构建不确定随机变量的矩母函数,下文对不确定理论和机会理论进行必要说明。
定义3[12] 假设Γ表示一个非空集合,




1) 
2) 

3) 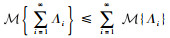
那么称


定义4[12] 假设γ表示从不确定空间(Γ, 

定义5[12] 假设不确定变量用γ表示,称

|
为γ的不确定分布。
定义6[13] 假设(Ω, 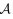
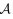




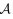
定义7[13] 假设ξ表示从机会空间(Γ, 

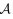
注释1 对于任意的实数集B,集合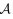

定义8[13] 假设ξ表示不确定随机变量,称
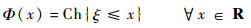
|
为ξ的机会分布。
注释2 随机变量的机会分布是随机变量的概率分布,不确定变量的机会分布是不确定变量的不确定分布。
风险度hi是不确定型风险分量和随机型风险分量的函数,即风险度hi是一个不确定随机变量,由该变量定义的矩母函数有如下性质:
性质1 如果不确定随机变量服从正则机会分布,那么该变量的矩母函数唯一确定。
性质2 不确定随机变量的矩母函数对于θ的一阶导数在θ=0处的值,即为不确定随机变量hi的期望。
定理1[15] 假设hi1, hi2, …, him表示服从不确定分布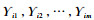
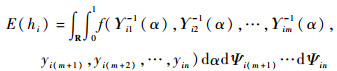
|
(3) |
注释3 假设不确定随机变量间满足:hi=hi1+hi2+…+him+hi(m+1)+hi(m+2)+…+hin,那么
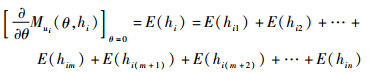
|
(4) |
注释4 假设不确定随机变量间满足:hi=hi1×hi2×…×him×hi(m+1)×hi(m+2)×…×hin,那么

|
(5) |
为了综合考虑系统的微观信息,引入如下参数对模型进一步分析。
定义9 假设pE=WE(θ)|θ=0表示UR-MTPGERT网络总路的等价实现机会,则称
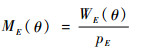
|
为UR-MTPGERT网络总路的等价矩母函数。
定义10 假设

定义11[11] 设风险度向量h(t)=(h1(t), h2(t), …, hn(t)),Ii(t)=əHE(h(t))/əhi(t)表示风险元的风险度变化引起复杂装备风险度HE变化的程度,则称Ii(t)为复杂装备风险元ui重要度。
定义12[11] 设Ik0={Iki|k = 1, 2, …, s}为第k个复杂装备风险路径的风险度向量集合,Ik={Ii(k)|k=1, 2, …, s}为被检测的风险度向量集合,称

|
(6) |
为复杂装备风险路径关联度。式中:ζ为分辨系数,一般取值为0.5。
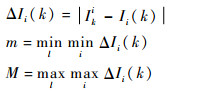
|
当该风险路径包含风险元ui风险时,Iki取值为1,Ii(k)取其风险重要度,否则Iki取值为0。
2 风险传导UR-MTPGERT网络模型求解 2.1 风险传导强度计算在复杂装备中,风险元之间相互影响,在风险元的共同作用下改变风险传导的流量,最终改变复杂装备的安全状况。风险元的影响作用既包括风险元间的相互影响,也包括风险元直接对整个系统安全产生影响。定义风险传导强度pij衡量风险元ui影响风险元uj发生的程度。风险传导强度pij值越大,子系统的传导能力就越强;定义风险传导强度piE衡量风险元ui对整个系统安全性的影响。
定义13[11] 设Gi和Gj分别为复杂装备风险元ui与uj的功效系数,αi和βi分别为复杂装备风险元ui风险度hi样本的上限值和下限值,η为调整系数,则称
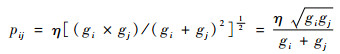
|
(7) |
为UR-MTPGERT节点-节点的风险传导强度。式中:
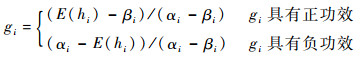
|
定义14 设μi为复杂装备风险元ui的功效系数,Ai和Bi分别为复杂装备风险元ui风险度hi样本的上限值和下限值,ϑ为调整系数,则称
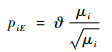
|
(8) |
为UR-MTPGERT节点-系统的风险传导强度。式中:
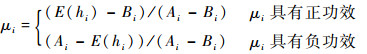
|
为了更客观地确定不确定变量的分布,需要结合多位专家的经验数据,本文采用德尔菲法对数据进行处理。确定经验不确定分布的步骤如下:
步骤1 已知m个领域专家的经验数据:(xij, αij), j=1, 2, …, ni, i=1, 2, …, m。
步骤2 根据第i个专家的经验数据(xi1, αi1),(xi2, αi2),…,(xini, αini)得到第i个专家的不确定分布函数
步骤3 多位专家经验数据可得多个不确定分布,综合多位专家的经验可得
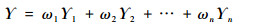
|
步骤4 如果满足|αij-Υ(xij)| < ε,ε为给定的任意小的数,可得不确定分布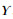
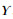
常见的不确定分布主要包括线性不确定分布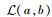
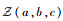
定理2 若不确定变量hi服从线性不确定分布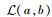
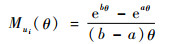
|
(9) |
证明 线性不确定分布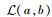
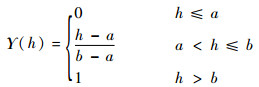
|
(10) |
逆分布为

|
(11) |
则其矩母函数为
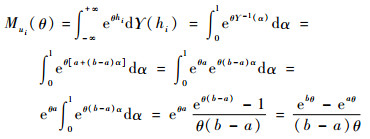
|
(12) |
证毕
定理3 若不确定变量hi服从之字形不确定分布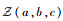
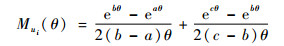
|
(13) |
证明 之字形不确定分布的分布函数为
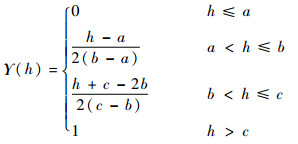
|
(14) |
逆分布为
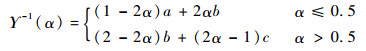
|
(15) |
则其矩母函数为
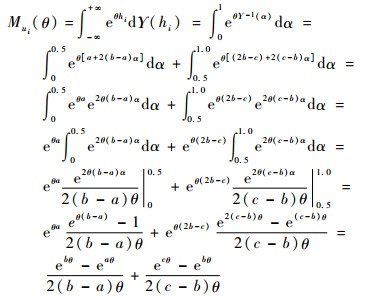
|
(16) |
证毕
定理4 若不确定变量hi服从经验不确定分布,则其矩母函数为

|
(17) |
证明 经验不确定分布的分布函数为

|
(18) |
式中:1≤i < n。
逆分布为
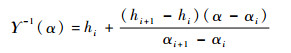
|
(19) |
式中:αi≤α≤αi+1, 1≤i < n。
则其矩母函数为
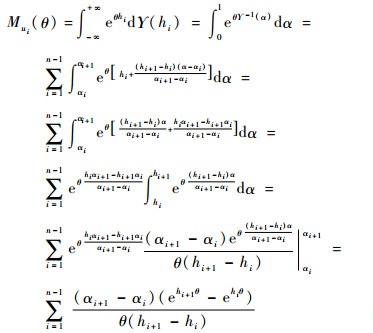
|
(20) |
证毕
2.3 极大熵法估计风险度概率密度极大熵模型是以概率密度函数的信息熵函数为目标函数,以数据样本X的各阶统计矩Mj为约束条件,在满足全部约束条件的情况下最大化目标函数的优化模型,构建的模型如下:
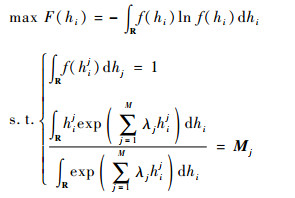
|
(21) |
式中:max F(hi)表示被求函数f(hi)的最小无偏估计,表达式为
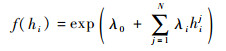
|
(22) |
式中:N为概率密度函数f(hi)已知矩的数量;hij为第j阶矩;λ0、λi(j=1, 2, …, N)为变分法引入的拉格朗日系数。
由式(22)知,解出拉格朗日系数λj(j=1, 2, …, N),风险度概率密度解析式就可以确定。
实际求解时难以求出解析解,一般通过数值方法进行求解,先构建极大熵改进的无约束规划模型,如式(23)所示,再采用智能算法对该规划模型进行求解。
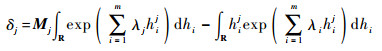
|
(23) |
满足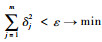
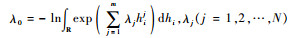
复杂装备的UR-MTPGERT网络求解比较复杂,应用梅森公式计算易出现遗漏和差错,并且计算量较大。为了适应网络的复杂性,充分发挥计算机的计算性能,根据文献[18]引入矩阵分析的方法进行计算。
n阶方程组的向量表示形式为
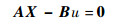
|
(24) |
该方程的解可以表示为
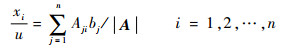
|
(25) |
式中:Aji为余子式。
根据文献[19]可知,流图可以用式(24)表示。GERT网络可以参照流图进行计算,假设GERT网络风险传导方向对应流图方向,风险流对应流图边线的权值,因流图要求流入系统节点的所有信号的和为零,则GERT网络节点间的传递系数构成的矩阵AS需要减去n阶单位矩阵,得到对应方程组的系数矩阵A。
因为矩阵A为稀疏矩阵,可采用Hash索引的方式储存索引相关变量;计算具体某个子系统对系统安全性影响时,特别是多输入多输出复杂系统,因为矩阵A中包括其他子系统信息,可将无关信息删除后再进行计算,以提高计算效率。
3 案例分析为了简单说明复杂装备安全性分析的基本过程,本文假设某型飞机主要由环控子系统、操纵子系统、结构子系统、液压子系统、供电子系统、导航子系统、推进子系统等7个子系统构成。每个子系统的风险主要从物理部件故障、人为失误、环境扰动、管理不到位安全意识薄弱等4个方面进行分析。前3个因素根据历史数据得到概率密度函数,第4个因素没有充足的数据,通过专家经验得到专家信度,分别记hi1、hi2、hi3、hi4为第i个子系统的风险度hi的风险分量,hi为不确定随机变量。
本文以操纵子系统为例,将操纵子系统的部件失效率数据作为物理部件风险度,该参数服从三参数威布尔分布,数值如表 1所示,利用极大熵模型求解其概率分布函数。
| 时段 | 风险度h1/10-6 |
| 1 | 0.42 |
| 2 | 0.58 |
| 3 | 0.57 |
| 4 | 0.22 |
| 5 | 0.80 |
| 6 | 0.35 |
| 7 | 0.87 |
| 8 | 0.64 |
| 9 | 0.56 |
| 10 | 0.59 |
| 11 | 0.38 |
| 12 | 0.55 |
| 13 | 0.63 |
| 14 | 0.65 |
| 15 | 0.69 |
| 16 | 0.80 |
| 17 | 0.57 |
| 18 | 0.39 |
| 19 | 0.89 |
| 20 | 0.61 |
| 21 | 0.49 |
| 22 | 0.61 |
| 23 | 0.31 |
| 24 | 0.58 |
量子菌群算法[20]将量子理论引入菌群算法(QBFO),有很强的全局搜索能力。但是固定的旋转相位不利于算法收敛,因此引入非线性自适应旋转角,利用改进的NAQBFO算法进行求解。优化曲线如图 3所示,利用QBFO、GA、NAQBFO算法同时求解该问题,得到迭代200次的对比图。通过比较可知,NAQBFO算法的收敛速度最快,精度最高;QBFO算法相比GA算法收敛速度更快,精度更高,NAQBFO算法的改进是有效的。

|
| 图 3 各算法优化曲线比较 Fig. 3 Comparison of optimization curves of various algorithms |
通过求解可以得到风险度概率密度函数和不确定分布为

|
根据以上对风险度机会分布的求解结果,可以进一步得到不确定随机变量的矩母函数。已知各风险元的风险属性的基础上,分析各个子系统之间的风险传导关系,可以建立某型飞机风险传导UR-MTPGERT网络示意图,如图 4所示,各个飞机子系统与网络模型图中代号的对应关系如表 2所示。

|
| 图 4 某型飞机风险传导UR-MTPGERT网络示意图 Fig. 4 Schematic of risk conduction UR-MTPGERT network of a certain type of aircraft |
| 代号 | 子系统 |
| 1 | 环控子系统 |
| 2 | 操纵子系统 |
| 3 | 结构子系统 |
| 4 | 液压子系统 |
| 5 | 供电子系统 |
| 6 | 导航子系统 |
| 7 | 推进子系统 |
对该模型矩阵化处理可得流图增益矩阵A,利用矩阵的相关理论结合计算机软件可以解得等效传递系数WE。矩阵A可以表示为

|
本文求解由风险元1~风险元8的风险传导系数,与风险元1直接作用的是风险元2和风险元4,分别求解其余子式和输入系数如下:
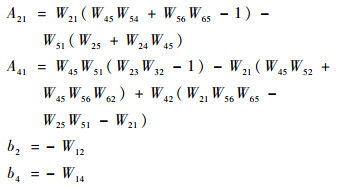
|
可以利用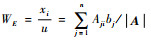
风险度的期望计算式为
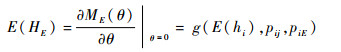
|
根据表 1和部队训练统计数据以及式(7)、式(8),可得各风险元间的风险传导强度为(p12, p14, p21, p23, p24, p25, p32, p45, p47, p54, p56, p57, p58, p62, p65, p78)=(0.006 3, 0.005 8, 0.006 9, 0.008 9, 0.007 1, 0.007 4, 0.005 9, 0.010 9, 0.000 8, 0.003 7, 0.004 7, 0.005 9, 0.012 5, 0.001 2, 0.092 1, 0.007 6)。
E(HE)可以通过对ME(θ)求导的公式求得,E(hi)可以通过注释3、注释4求得。本文以hi=hi1+hi2+hi3+hi4为例,求解说明该方法的有效性。根据上文求得的不确定随机变量的矩母函数和风险传导强度,可以对该风险传导模型分析如下:
1) 根据定义10,可以得到该型战机的总风险度为HE=3.562×10-8,持续对该型战机的各种风险状况进行评估,可以得到复杂装备总风险度的趋势图,在趋势图中通过设定临界风险点,可对任务的风险度进行预警。
2) 假设Mui(θ)=0,i=2, 3, 4,根据定义11可以解得,I1=0.009, I2=0.313,I3=0.121,I4=0.45,I5=0.482,I6=0.015, I7=0.561。I5>I7>I4>I2>I3>I6>I1表明该型飞机中,供电子系统对飞机安全性的影响最大,推进子系统对飞机安全性的影响较大,液压子系统和操纵子系统对飞机安全性的影响次之,结构子系统、导航子系统和环控系统对飞机安全性的影响相对较小。
3) 由于该实例风险路径比较复杂,本文以路径1(1→4→7→8)和路径2(1→2→5→8)为例,对风险路径的关联度进行分析。路径1和路径2的风险向量假设为{0, 1, 0, 1, 0}、{0, 0, 1, 1, 0}。根据15时段训练数据,以及定义12可得γ1=0.759,γ2=0.549。γ1>γ2说明风险路径1发生的可能性更大,需要加强液压子系统的检查维修,防止飞机降落过程中出现意外情况;同时需要加强推进子系统的检修,翻看检修记录,检查是否达到大修时限。
4 结论本文主要从模型变量和求解方法2个方面对模型进行改进,对装备风险传导进行分析。
1) 针对复杂装备中存在的非决定现象,基于机会理论,提出不确定随机变量的矩母函数,搭建了多风险因素风险传导分析框架,构建了UR-MTPGERT网络。
2) 引入风险元重要度、风险路径关联度等参数,从微观角度分析风险元对复杂装备整体风险度的影响,有利于找到复杂装备的脆弱点,对下一步安全控制提供指导。
3) 运用德尔菲法求解经验不确定分布;运用极大熵模型求解任意随机变量的概率分布;引入矩阵分析技术,解决了模型传递参数求解困难的问题,为下一步利用计算机编程处理复杂装备风险问题做好铺垫。
下一步,在本文的基础上还需针对风险度的特定数值对系统的风险等级进行划分,同时针对不同的风险等级提出相应的风险控制方案,以更好地实现安全控制。
| [1] |
闻敬谦, 李青. 基于工作流的航空装备综合维修保障管理[J].
计算机集成制造系统, 2010, 16 (10): 2196–2205.
WEN J Q, LI Q. A comprehensive maintenance support management of aviation equipment based on workflow[J]. Computer Integrated Manufacturing Systems, 2010, 16 (10): 2196–2205. (in Chinese) |
| [2] |
查尔斯·佩罗.
高风险技术与"正常事故"[M]. 北京: 科学技术文献出版社, 1988.
PERROW C. High-risk technology and "normal" accidents[M]. Beijing: Science and Technology Literature Press, 1988. (in Chinese) |
| [3] |
郭鹏. 航空武器装备全寿命周期风险评估方法比较与改进[J].
航空学报, 2003, 24 (5): 427–430.
GUO P. Comparison and improvement of life-cycle risk assessment methods for aviation weapon equipment[J]. Acta Aeronautica et Astronautica Sinica, 2003, 24 (5): 427–430. DOI:10.3321/j.issn:1000-6893.2003.05.010 (in Chinese) |
| [4] | LI C, WANG K. The risk element transmission theory research of multi-objective risk-time-cost trade-off[J]. Computers & Mathematics with Applications, 2009, 57 (11-12): 1792–1799. |
| [5] | LI X, ZHAO T, RONG M. A multi-factor coupling event chain model based on Petri nets[C]//International Conference on Reliability, Maintainability and Safety. Piscataway, NJ: IEEE Press, 2009: 466-469. |
| [6] |
李晓磊, 田瑾, 赵廷弟. 改进的区域安全性分析方法[J].
航空学报, 2008, 29 (3): 622–626.
LI X L, TIAN J, ZHAO T D. An improved method of regional safety analysis[J]. Acta Aeronautica et Astronautica Sinica, 2008, 29 (3): 622–626. DOI:10.3321/j.issn:1000-6893.2008.03.014 (in Chinese) |
| [7] | QU J F, LI G, ZHANG S L. Study on system coupling effects of ecological and economic in mining subsidence reclamation area[J]. Advanced Materials Research, 2013, 610-613 : 1315–1320. |
| [8] | LUO P, HU Y. System risk evolution analysis and risk critical event identification based on event sequence diagram[J]. Reliability Engineering & System Safety, 2013, 114 (1): 36–44. |
| [9] | MIGUEL A, BEDIA M G, BARANDIARAN X E. Extended neural metastability in an embodied model of sensorimotor coupling[J]. Frontiers in Systems Neuroscience, 2016, 10 (117): 76. |
| [10] | PRITSKER A. Graphical evaluation and review technique[M]. Berlin: Springer, 2001. |
| [11] |
李超, 王瑛, 陈超, 等. 基于QHSME的装备危险耦合传导GERT分析[J].
系统工程与电子技术, 2014, 36 (11): 2219–2225.
LI C, WANG Y, CHEN C, et al. GERT analysis of coupled conduction for materiel hazard based on QHSME[J]. Systems Engineering & Electronics, 2014, 36 (11): 2219–2225. DOI:10.3969/j.issn.1001-506X.2014.11.17 (in Chinese) |
| [12] | LIU B. Uncertainty distribution and independence of uncertain processes[J]. Fuzzy Optimization & Decision Making, 2014, 13 (3): 259–271. |
| [13] | LIU B, CHEN X. Uncertain multiobjective programming and uncertain goal programming[J]. Journal of Uncertainty Analysis & Applications, 2015, 3 (1): 1–8. |
| [14] | LIU Y, HA M. Expected value of function of uncertain variables[J]. Journal of Uncertain Systems, 2010, 3 (4): 181–186. |
| [15] | LIU B, YAO K. Uncertain multilevel programming:Algorithm and applications[J]. Computers & Industrial Engineering, 2015, 89 : 235–240. |
| [16] | PHILLIPS S J, ANDERSON R P, SCHAPIRE R E. Maximum entropy modeling of species geographic distributions[J]. Ecological Modelling, 2006, 190 (3-4): 231–259. DOI:10.1016/j.ecolmodel.2005.03.026 |
| [17] | YEO G, BURGE C B. Maximum entropy modeling of short sequence motifs with applications to RNA splicing signals[J]. Journal of Computational Biology:A Journal of Computational Molecular Cell Biology, 2004, 11 (2-3): 377–394. DOI:10.1089/1066527041410418 |
| [18] |
陶良彦, 刘思峰, 方志耕, 等. GERT网络的矩阵式表达及求解模型[J].
系统工程与电子技术, 2017, 39 (6): 1292–1297.
TAO L Y, LIU S F, FANG Z G, et al. Matrix expression and solution model of GERT network[J]. Systems Engineering and Electronics, 2017, 39 (6): 1292–1297. (in Chinese) |
| [19] |
罗涛. 信号与系统分析的流图矩阵法[J].
通信学报, 1993, 14 (6): 73–79.
LUO T. Analysis of signals and systems by flow graph matrix method[J]. Journal of China Institute of Communications, 1993, 14 (6): 73–79. (in Chinese) |
| [20] |
刘璐, 单梁, 戴跃伟, 等. 非线性动态自适应旋转角的量子菌群算法[J].
控制与决策, 2017, 32 (12): 2137–2144.
LIU L, SHAN L, DAI Y W, et al. Quantum germ algorithm for nonlinear dynamic adaptive rotation angle[J]. Control & Decision, 2017, 32 (12): 2137–2144. (in Chinese) |



