飞机结冰会对飞行安全产生严重影响,对于亚声速飞机,由于气动加热效果不明显,因此一般都会在重要迎风部件安装有防除冰系统。现有的防除冰系统中,热气防冰系统是使用最为广泛,系统可靠性最高的系统[1]。系统所用热气引自发动机压气机,高温热气通过分配管路进入各防护区域,加热蒙皮,以将撞击到蒙皮表面的过冷水蒸发,从而达到防冰的效果。
评估热气防冰系统性能的有效方法包括冰风洞试验、自然结冰试验和数值仿真计算,其中冰风洞试验耗资较大,且冰风洞所能达到的环境条件是有限的,不能完全满足系统设计的需求;而自然结冰试验属于危险科目,必须在系统经过了较为充分的验证后方可进行,因此在设计阶段不能通过自然结冰试验实现对系统性能的验证。在热气防冰系统的设计和试验验证中,数值仿真方法可发挥重要的作用,系统参数的确定、系统的性能仿真以及系统设计优化等均可借助数值仿真的方法来进行。
在众多参数中,防冰表面温度是评价防冰系统性能的最重要指标。而防冰表面温度的计算过程复杂,涉及热气防冰腔内外流场的流固耦合计算。其中,防冰表面流动更是涉及气、固、液三相复杂传热流动计算,建立合理准确的数学模型是计算结果准确性的关键。目前国内外关于防冰表面水膜的流动模型大都建立在Messinger结冰热力学模型的基础上[2-4],国外FENSAP-ICE软件[5-6]基于计算得到的空气-壁面剪切力,建立水膜流动模型,并通过内外流场的松散耦合计算得到了防冰表面温度,并可用于三维计算;李延和郭涛[7]将等直机翼防冰腔部流动简化为二维流动,防冰腔内部仍为三维流动,通过内外的松散耦合计算得到了防冰表面温度信息。卜雪琴、侯盼雪等[8-9]基于FLUENT的用户自定义函数(UDF)功能建立了等直机翼和后掠翼的防冰表面温度计算的强耦合模型;郁嘉等[10]采用类似FENSAP-ICE软件的方法,求解空气流场获取防冰表面剪切力,并计算剪切力驱动下的水膜流动,从而进行内外流场的耦合。
本文提出了一种计算防冰表面温度的新方法,基于FLUENT软件的欧拉壁面液膜(EWF)模型[11]对水膜的动态流动过程进行模拟,通过求解空气驱动下的水滴流动场得到水滴收集特性,二者结合建立防冰表面热力学模型,进而采用松散耦合的方式进行内外流场的耦合计算,最终计算得到防冰表面温度分布和水膜厚度分布等防冰性能的重要评价指标。
1 数学模型 1.1 内外空气流场及蒙皮导热计算空气流场的计算通过求解Navier-Stokes方程进行,湍流模型选用S-A模型,用于内外流场的初始化计算。在外流场计算中,模型壁面设置为温度边界条件;内流场和蒙皮导热同时计算,其中蒙皮表面边界条件为对流边界条件。
1.2 水滴撞击特性的计算水滴收集特性通过求解空气驱动下的水滴场实现,控制方程为[12-15]

|
(1) |
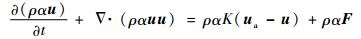
|
(2) |
式中:t为时间;ρ为水滴密度;α为水滴体积分数;u为水滴速度矢量;ua为空气速度矢量;F为作用在水滴上除阻力以外的外力;K为空气和水滴的动量交换系数,其表达式为

|
(3) |
其中:μa为空气的动力黏度;d为水滴直径;f为水滴的阻力系数,可按球形且不变形水滴的阻力系数计算,表达式为

|
(4) |
式中:Rer为空气和水滴的相对雷诺数,可用式(5)计算:

|
(5) |
其中:ρa为空气密度。
在水滴撞击特性的计算中,忽略方程中的非稳态项,方程的求解通过FLUENT的用户自定义标量(UDS)功能实现方程的求解,通过在连续性方程右侧添加数值扩散项消除局部计算结果的奇异现象,添加的数值扩散项为[15]

|
(6) |
式中:a根据经验取为0.001[15];b为当前网格与其周围相邻网格水滴体积分数的偏离程度,

|
(7) |
式中:k为相邻网格的个数;下标P表示当前网格;下标Ni表示当前网格相邻的网格。
求解增加了数值扩散相Г的式(1)和式(2)即可得到水滴体积分数在计算域内的分布,进而利用式(8)计算得到防冰表面的局部收集系数为

|
(8) |
式中:n为表面微元的外法向量;V∞为空气的来流速度。
在进行防冰腔水膜流动计算时,得到局部收集系数后,进而可计算得到各微元的水收集率

|
(9) |
式中:LWC为液态水含量;ds为微元的底面积。
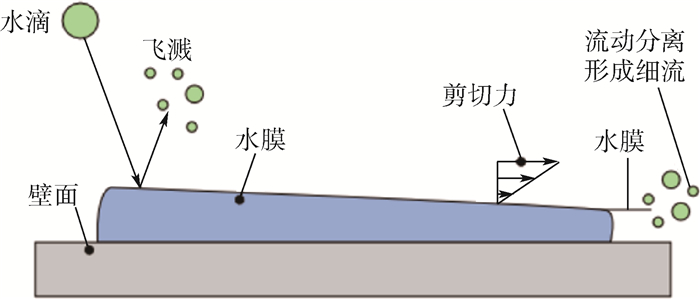
1.3 EWF模型及防冰表面热载荷的计算 1.3.1 EWF模型如图 1所示,云层中的过冷水滴会撞击到防冰表面,而在表面形成水膜,如果水滴较大,则会发生水滴的破碎、飞溅等现象,水膜在流动过程中受壁面剪切力、空气压力以及表面张力和自身黏性的影响,在特定的条件下,水膜的流动会由于表面张力的作用而发生分离,从而形成细流。本文所使用的EWF模型可以计算以上各种条件下的水膜流动,而对于本文所研究的防冰表面性能耦合计算的问题,暂不考虑过冷大水滴问题才会涉及的水滴的破碎、飞溅[16],同时假设水膜流动是连续的,不考虑水膜形成细流的问题。
|
| 图 1 防冰表面水的流动 Fig. 1 Water flow on anti-icing surface |
对于防冰表面的水膜流动而言,水膜厚度相对蒙皮表面的曲率半径而言是一个微小量,沿水膜厚度方向的物理属性可认为不发生变化,同时水膜的流动可认为平行于蒙皮表面,而无垂直方向的流动。在此基础上建立水膜流动的质量、动量、能量方程[11]:

|
(10) |

|
(11) |

|
(12) |
式中:h为水膜厚度;∇s为表面梯度算子;V1水膜速度矢量;ρl为水膜密度;

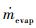
容易看出,欧拉水膜模型可同时计算在壁面压力梯度、重力、表面张力、剪切力、液体黏性力以及外界其他因素作用下的水膜流动,相比文献[7-9]中的算法,考虑的因素更加全面,更加接近实际物理过程。
对于防冰表面的水膜流动而言,可忽略重力、黏性力、液滴撞击等因素的影响,由此动量方程可简化为
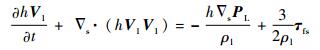
|
(13) |
在本文的计算模型中,由于水膜的温度同时由防冰腔内部和外部的换热决定,因此欧拉水膜的能量方程不能直接用于系统的耦合计算,需要根据防冰表面的换热分析建立内外流场的耦合换热模型,具体见1.4节。
1.3.2 防冰表面热载荷的计算根据经典的Messinger结冰热力学模型[17],防冰表面热流Qanti包括对流换热热流Qconv、水滴撞击热流Qcap、水蒸发吸收的热量Qevap以及从微元中流入和流出的水携带的能量,其中流入流出微元的液态水携带的能量差值取决于不同微元间的温度差,一般而言,相邻微元间的温度差别并不明显,因此相比较于前4项热流,流入流出控制体的能量变化可以忽略,因此防冰表面的热载荷可表示为

|
(14) |
对流换热热流的计算可直接通过求解Navier-Stokes方程的能量方程获得,水滴撞击热流包括水滴的动能和加热水滴至水膜温度的能量:

|
(15) |
式中:T∞为来流温度。
水的蒸发吸收的热量取决于水膜蒸发率

|
(16) |
式中:cpa为空气的定压比热容;P∞为环境静压;Te为附面层厚度处的空气温度;Pe为附面层厚度处的静压;e为饱和水蒸汽压;hconv为表面对流换热系数,可根据求解Navier-Stokes方程的能量方程获得的表面对流换热热流计算得到:

|
(17) |
其中:Trec为附面层恢复温度。
e(T)的计算式为[18]

|
(18) |
式中:T为温度。
计算得到防冰表面热流后,采用等效对流换热系数heff作为内流场和蒙皮导热的边界条件:

|
(19) |
式中:Tref为参考温度,可设置为环境温度,此处参考温度应与内流场对流边界条件设置的参考温度一致。
1.4 耦合换热模型的建立 1.4.1 水膜流动过程中的热载荷计算本文水膜流动的质量和动量守恒方程的求解借助FLUENT软件的EWF模型进行,将水滴收集率、蒸发率作为水膜流动的边界条件,并设置合理的时间步长,捕捉水膜在不同时间的厚度分布,同时通过编写UDF在每个时间步长更新水膜流动的边界条件,并以CFL数的变化量小于设定值作为计算收敛的标志,其中CFL数的定义为

|
(20) |
式中:uf、vf、wf分别为水膜的在x、y、z方向的流速;Δt为时间步长;Δx、Δy、Δz分别为相邻微元中心点距离在x、y、z方向的分量。
在每个时间步长内,对于每个微元进行如下计算:
1) 获取当前微元的水膜厚度和微元面积,计算得到当前微元上水膜的质量为

|
(21) |
2) 根据水滴收集特性计算结果,计算当前时间步长Δt内微元收集的水量为

|
(22) |
3) 计算当前微元在时间步长内的理论蒸发量Mevap。
4) 计算微元的质量源流量:

|
(23) |
5) 若Msource < 0, 则进一步比较|Msource|和Mf的大小:

|
(24) |
6) 计算得到质量源流量后,进一步根据1.3.2节的方法计算每个微元的等效对流换热系数,并设置用户自定义存储(UDM)将等效对流换热系数存储在计算文件中。
7) 计算CFL数,并将其与前一步长的CFL数进行对比,当残差小于设定值时,即可认为水膜流动达到了稳定状态,以此时计算得到的等效对流换热系数作为防冰表面热载荷的计算结果,将其作为内流场和蒙皮导热计算的边界条件。
1.4.2 界面数据的交换为便于工程计算,内外流场交界面处的网格节点并非一一对应,因此进行内外流场的数据交换时,需采用合理的插值方法进行,本文借助FLUENT软件的profiles功能,可选用2种不同的插值方法,分别为最小距离法和反距离加权插值[19],二者的基本原理如下:最小距离法是将已知网格中与待定节点距离最小的节点数据作为待定节点的数据;反距离加权插值是将待定节点与已知节点间距离乘方的倒数作为权值,计算待定节点的数据信息。
本文在计算时,采用反距离加权插值方法。
1.4.3 耦合收敛的控制对于内外流场的耦合,若直接将计算得到的蒙皮温度分布或等效对流换热系数分布作为内外侧流场计算的边界条件,会导致数值的波动而无法达到收敛,因此在实际计算时引入亚松弛因子。
在本文的计算中,仅对等效对流换热系数引入亚松弛因子ω:

|
(25) |
式中:hefft和heffti-1分别为当前和前一时间步的等效对流换热系数。
2 算例分析 2.1 计算模型和计算状态为验证本文计算方法的准确性,计算了某民机发动机短舱防冰系统的防冰性能。其中防冰腔采用旋流喷嘴的形式,热空气从喷嘴中喷出,在防冰腔的环形通道中循环流动,充分换热后从防冰腔后壁板上的开孔排出机外。根据几何模型分别对外流场和内流场(含蒙皮)划分网格,并计算流场作为耦合计算的初值。

|
| 图 2 短舱几何外形及其防护区域 Fig. 2 Nacelle's geometric shape and protection area |
|
| 图 3 短舱防冰腔 Fig. 3 Nacelle anti-icing chamber |
计算采用的外部环境和供气参数见表 1。
| 参数 | 马赫数 | 环境压力/Pa | 环境温度/℃ | 水滴直径/μm | 液态水含量/(g·m-3) | 供气压力/kPa | 供气温度/℃ |
| 数值 | 0.3 | 70 124 | -9.4 | 20 | 0.5 | 350 | 150 |
2.2 水滴撞击特性
在空气流场的基础上,采用1.2节中方法求解水滴流动的UDS方程,其中离散格式采用二阶迎风格式以保证足够的计算精度,将局部收集系数存储在FLUENT软件UDM中,作为水膜流动的边界条件之一。求解水滴流场得到的局部收集系数结果和在相同条件下用FENSAP-ICE软件计算得到的局部水滴收集系数计算结果见图 4。

|
| 图 4 水滴局部收集系数计算结果的对比 Fig. 4 Comparison of water droplet local collection coefficient |
从二者的对比结果可以明显看出,本文与FENSAP-ICE软件的计算结果基本相同,因此本文采用的基于FLUENT软件UDS的水滴场求解方法是正确的,此方法可以用于任意三维部件水滴撞击特性的计算。
2.3 水膜流动的动态过程在计算水膜流动时,根据1.4.1节编写UDF文件,将求得的水质量流量源项加载至壁面(含防护区域和非防护区域),计算不同时间步内水膜流动的动态过程,其中内流场和蒙皮导热计算得到的蒙皮表面温度作为温度边界条件,时间步长为0.03 s,图 5为部分时刻水膜厚度的计算结果。

|
| 图 5 不同时刻的水膜厚度分布 Fig. 5 Water film thickness distribution at different time |
从不同时刻的水膜厚度分布可以看出如下规律,在初始阶段,由于水滴的撞击水膜厚度逐渐增长,但由于收集量较少,水膜仅分布在前缘水滴撞击区域;随着时间的累积,收集量逐渐增大,但撞击区域的加热热流并不能使收集到的水蒸发,因此水膜沿壁面向后溢流,由于撞击区域后不再有水滴的撞击,但加热热流仍会使流入该区域的水膜蒸发;最终在一定时间后,整个防护区域的水膜厚度在水滴撞击、加热蒸发、水膜流动等因素的作用下趋于稳定。
此外,若加热热流不足以使所收集的液态水在防护区域内蒸发,则水膜会流出防护区域外,在此区域没有加热热流,因此水膜会迅速冻结,形成溢流冰。在本文的计算条件下,水膜有极少量流出了防护区域,如图 6所示,因此会在形成溢流冰,关于溢流冰外形及厚度的计算,将在后续研究工作中开展。

|
| 图 6 防护区域外的水膜厚度分布 Fig. 6 Water film thickness distribution in non-protection area |
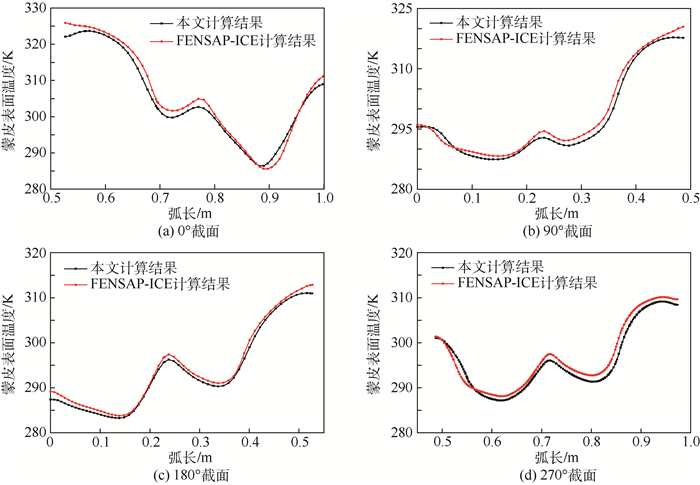
防冰表面温度是评价热气防冰系统性能的重要参数,本文通过内外流场、水膜流动及防冰热载荷等参数的耦合计算,得到了收敛后的短舱防护区域蒙皮表面温度分布,同时用FENSAP-ICE软件计算了相同模型下的防冰表面温度,二者的对比见图 7,同时沿周向截取了4个截面进行温度分布的对比,见图 8。

|
| 图 7 加热区域蒙皮表面温度分布对比 Fig. 7 Comparison of skin temperature distribution of heated area |
|
| 图 8 不同截面蒙皮表面温度分布对比 Fig. 8 Comparison of skin temperature distribution on different sections |
从蒙皮表面温度计算结果可以看出,计算收敛后的最高温度为329.7 K,最低温度为281.4 K,最低温度大于冰点,表明在整个防护区域内未出现结冰现象。而最高温度出现在外侧上部区域,这是由于气流喷射引起的局部高温;整个防护区域内低温出现的位置为远离前缘的区域,在此区域存在气流加速引起的对流换热系数的增加,从而导致散热量增大而造成此区域温度较低。
从FENSAP-ICE软件的计算结果与本文计算结果的对比可以明显看出二者具有较高的一致性,可以验证本文计算方法的正确性。
计算收敛后的等效对流换热系数分布见图 9。可以看出,在前缘驻点区域,由于流动为层流导致对流换热系数较小,进而导致水的蒸发量很小。由于对流换热和蒸发散热是防冰热载荷的决定因素,因此在前缘驻点区域,等效对流换热系数很小。而在驻点往后的区域,等效对流换热系数受空气对流换热、蒸发散热、水滴撞击携带热量以及水膜流动换热的综合作用。此外由于水膜溢流区域以外无水膜的蒸发散热,导致此区域等效对流换热系数迅速减小。

|
| 图 9 等效对流换热系数分布 Fig. 9 Distribution of equivalent convective heat transfer coefficient |
本文基于FLUENT软件EWF模型提出了一种热气防冰腔性能仿真计算的新方法,通过对算例的对比和分析表明:
1) 基于UDS的水滴撞击特性计算方法的计算结果与FENSAP-ICE软件计算结果基本相同,可满足三维表面水滴撞击特性的计算。
2) 提出了基于EWF模型结合UDF自定义质量流量边界条件求解水膜在防冰表面的动态流动过程方法,实现了三维水膜的流动及传热计算,结果真实可信。
3) 建立了适应于三维外形的防冰性能换热计算模型,并通过算例计算得到了某民机发动机短舱防冰系统在典型外部环境和供气参数下的三维防冰表面温度、防冰表面水膜厚度分布以及表征防冰热载荷的等效对流换热系数。通过对算例计算结果的分析和对比可知,本文提出的基于EWF模型的热气防冰腔性能仿真计算方法是切实有效的,其计算结果也是合理可信的。
后续将在本文研究内容的基础上开展计算结果的试验验证以及溢流冰仿真研究工作。
| [1] |
林贵平, 卜雪琴, 申晓斌, 等.
飞机结冰与防冰技术[M]. 北京: 北京航空航天大学出版社, 2016: 30-46.
LIN G P, BU X Q, SHEN X B, et al. Aircraft icing and anti-icing technology[M]. Beijing: Beihang University Press, 2016: 30-46. (in Chinese) |
| [2] | DONG W, ZHU J, MIN X H. Calculation of the heat transfer and temperature on the aircraft anti-icing surface[C]//27th International Congress of the Aeronautical Sciences, 2010: 1-9. |
| [3] | DOMINGOS R H, PAPADAKIS M, ZAMORA A O. Computational methodology for bleed air ice protection system parametric analysis: AIAA-2010-7834[R]. Reston: AIAA, 2010. |
| [4] | MORENCY F, BRAHIMI M T, TEZOK F, et al. Anti-icing system simulation using CANICE[J]. Journal of Aircraft, 1999, 36 (6): 999–1006. DOI:10.2514/2.2541 |
| [5] | PELLISSIER M, HABASHI W G, PUEYO A. Design optimization of hot-air anti-icing systems by FENSAP-ICE: AIAA-2010-1238[R]. Reston: AIAA, 2010. |
| [6] | WANG H Z, TRAN P, HABASHI W G. Anti-icing simulation in wet air of a piccolo system using FE NSAP-ICE: SAE 2007-01-3357[R]. Warrendale: SAE International, 2007. |
| [7] |
李延, 郭涛. 基于松散耦合的三维热气防冰腔数值仿真[C]//第六届中国航空学会青年科技论坛文集. 北京: 航空工业出版社, 2014: 1245-1250.
LI Y, GUO T. Numerical simulation of three dimensional thermal anti-icing chamber by loose couple method[C]//CSAA the sixth Youth Science and Technology Forum. Beijing: Aviation Industry Press, 2014: 1245-1250(in Chinese). |
| [8] |
卜雪琴, 林贵平, 郁嘉. 三维内外热耦合计算热气防冰系统表面温度[J].
航空动力学报, 2009, 24 (11): 2495–2500.
BU X Q, LIN G P, YU J. Three dimensional conjugate heat transfer for the surface temperature of wing hot-air anti-icing system[J]. Journal of Aerospace Power, 2009, 24 (11): 2495–2500. (in Chinese) |
| [9] |
侯盼雪, 林贵平, 卜雪琴, 等. 后掠翼热气防冰系统数值仿真[J].
航空学报, 2012, 33 (5): 809–817.
HOU P X, LIN G P, BU X Q, et al. Numerical simulation of a swept wing hot-air anti-icing system[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33 (5): 809–817. (in Chinese) |
| [10] |
郁嘉, 赵柏阳, 卜雪琴, 等. 某型飞机发动机短舱热气防冰系统性能数值模拟[J].
空气动力学学报, 2016, 34 (3): 302–307.
YU J, ZHAO B Y, BU X Q, et al. Numerical simulation of the performance of an engine nacelle hot-air anti-icing system[J]. Acta Aerodynamica Sinica, 2016, 34 (3): 302–307. (in Chinese) |
| [11] | Ansys Inc. ANSYS FLUENT 14 User Guide[Z]. New Hampshire: ANSYS Inc., 2011. |
| [12] |
毛晓东, 卜雪琴, 赵国昌, 等. 基于UDS框架的水撞击特性数值计算方法[J].
沈阳航空航天大学学报, 2016, 33 (1): 8–12.
MAO X D, BU X Q, ZHAO G C, et al. Calculation of water droplet impingement characteristics based on UDS frame[J]. Journal of Shenyang Aerospace University, 2016, 33 (1): 8–12. (in Chinese) |
| [13] | WIROGO S, SRIRAMBHATLA S. An eulerian method to calculate the collect efficiency on two and three dimensional bodies: AIAA-2003-1073[R]. Reston: AIAA, 2003. |
| [14] | TONG X L, LUKE E A. Eulerian simulations of icing collection efficiency using a singularity diffusion model: AIAA-2005-1246[R]. Reston: AIAA, 2005. |
| [15] |
杨胜华, 林贵平, 申晓斌. 三维复杂表面水滴撞击特性计算[J].
航空动力学报, 2010, 25 (2): 284–290.
YANG S H, LIN G P, SHEN X B. Water droplet impingement prediction for three dimensional complex surfaces[J]. Journal of Aerospace Power, 2010, 25 (2): 284–290. (in Chinese) |
| [16] |
王超, 常士楠, 吴梦龙, 等. 过冷大水滴飞溅特性数值分析[J].
航空学报, 2014, 35 (4): 1004–1011.
WANG C, CHANG S N, WU M L, et al. Numerical investigation of splashing characteristics in super-cooled large droplet regime[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35 (4): 1004–1011. (in Chinese) |
| [17] | MESSINGER B L. Equilibrium temperature of an unheated icing surface as a function of air speed[J]. Journal of the Aeronautical Sciences, 1953, 20 (1): 29–42. DOI:10.2514/8.2520 |
| [18] | VELAZQUEZ M T, HANSMAN R J. Implementation of combined feather and surface-normal ice growth models in LEWICE/X: AIAA-1995-0735[R]. Reston: AIAA, 1995. |
| [19] |
陈鹏, 邓飞, 刘思亭. 三维空间属性插值方法的研究[J].
电脑知识与技术, 2015, 11 (7): 235–239.
CHEN P, DENG F, LIU S T. Research of three dimensional space attribute interpolation methods[J]. Computer Knowledge and Technology, 2015, 11 (7): 235–239. (in Chinese) |



