作为在轨空间站的重要组件,太阳能帆板担负着为整个空间站供电的任务。为提高太阳能转化效率,太阳能帆板驱动系统(SADS)的角位置控制吸引了很多学者的深入研究。然而,太阳能帆板是柔性体,其动态特性包含了大量与刚体运动相耦合的弱阻尼柔性模态。该特性极易在系统的对日定向过程中引起太阳能帆板的柔性振动,进而影响空间站的运动与控制。因此, 寻求一种角位置控制和振动抑制方法对于太阳能帆板驱动系统显得尤为重要。
针对太阳能帆板的振动抑制问题,国内外学者做了大量研究。采用智能材料进行主动控制是一种有效抑制振动的方法。在基于智能材料的控制方法方面,提出了刚度控制[1]以及正位置反馈控制[2-3]。然而,这类方法需要在原结构上附加一系列的传感器和作动器,增加了系统的质量,同时降低了可靠性,因此该主动控制方法在空间系统的实际应用中受到一定限制[4]。另一种抑制振动的方法是输入成形,该方法将期望指令与脉冲序列在时域中进行卷积,所形成的新指令作为系统输入来控制系统的运动以消除柔性模态的振动[5]。文献[6]将输入成形器(IS)应用于太阳能帆板驱动系统的振动抑制中,提升了系统的工作性能。然而,输入成形器的设计依赖于太阳能帆板驱动系统的数学模型,由于系统存在不确定性,该数学模型难以准确建立[7]。不仅如此,输入成形器是基于线性系统理论设计的,无法直接应用于非线性系统[8-9]。
太阳能帆板驱动系统的角位置控制同样被广泛研究。文献[10]针对太阳能帆板驱动系统提出一种H∞鲁棒控制。文献[11-12]和文献[13-14]针对刚柔耦合系统分别设计了自适应控制和滑模控制,文献[15]基于耗散理论提出一种主动稳定器。以上控制方法都能在完成指定的角位置阶跃响应的同时抑制柔性振动,并且缩短了过渡过程时间,提高了系统性能对参数摄动与外部干扰的鲁棒性。然而,由于缺少对指令轨迹的设计,使得系统在瞬态过程中存在较大的柔性振动。文献[16-18]针对刚柔耦合系统分别提出了带自适应律和不带自适应律的滑模控制,并且采用基于参考模型的输入成形器设计了系统的指令轨迹。该方法通过滑模控制令太阳能帆板驱动系统表现得像参考模型。这种方法的参考模型属于多维度系统,为获得输入成形器预期的振动抑制效果,滑模控制在保证系统角位置和角速度跟踪参考轨迹的同时还要保证系统的模态坐标跟踪参考模型的模态坐标,增加了控制设计的复杂性和计算成本。
基于上述讨论,本文提出一种自适应滑模控制(ASMC)与输入成形技术相结合的控制策略。该控制策略通过自适应滑模控制保证了系统在不确定性影响下的一致有界性和渐进一致有界性,从而提高了太阳能帆板驱动系统的角位置控制性能。同时,通过基于参考模型的输入成形器规划了系统的指令轨迹,进而抑制了太阳能帆板的柔性振动。本文首先建立了太阳能帆板驱动系统的数学模型,其次提出了包含输入成形器、参考模型和自适应滑模控制的控制策略,最后给出了仿真结果。
1 太阳能帆板驱动系统数学建模太阳能帆板驱动系统包含伺服电机、减速器、太阳能帆板等,其简化结构如图 1所示。驱动系统的轮毂上固结了2个对称配置的柔性帆板,电机产生力矩驱动柔性帆板旋转[19]。将轮毂视为刚体且将太阳能帆板视为欧拉-伯努利梁,利用假设模态法,可以得到帆板的横向弯曲挠度表达式如下:
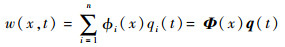
|
(1) |

|
| 图 1 太阳能帆板驱动系统结构 Fig. 1 Structure of SADS |
式中: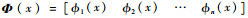

|
(2) |
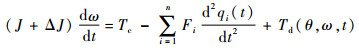
|
(3) |
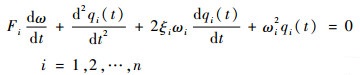
|
(4) |
式中:θ为系统角位置;ω为系统角速度;J为伺服电机、减速器、轮毂和太阳能帆板的总转动惯量;ΔJ为转动惯量的不确定性;Fi为第i阶模态的耦合系数;Tc为作用在减速器输出轴上的驱动力矩;Td(θ, ω, t)为外界干扰力矩(如摩擦力矩);ξi为第i阶模态的阻尼比;ωi为第i阶模态的角频率;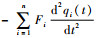
需要指出的是,式(2)和式(3)构成太阳能帆板驱动系统的刚体子系统,式(4)为柔性体子系统。根据式(2)和式(3)可知,刚体子系统包含非线性项Td(θ, ω, t),是一个非线性系统。根据式(4)可知,柔性体子系统是线性的。
当表贴式永磁同步电机(SPMSM)作为系统的伺服电机时,电机的转矩方程和电压方程可以写为[21]
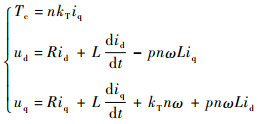
|
(5) |
式中:ud、uq、id、iq、R和L分别表示电机在d-q轴系下的定子电压、定子电流、定子电阻和定子电感;n为减速器传动比;p为电机的极对数;kT为电机的转矩常数。
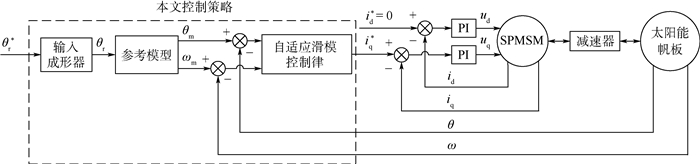
2 控制系统设计本文所设计的太阳能帆板驱动系统采用位置-电流双闭环控制结构,如图 2所示,θr*、θr和θm分别为角位置期望指令、成形后的角位置指令和参考模型的角位置;ωm为参考模型的角速度;id*和iq*分别为电机的d轴和q轴电流指令。其中,位置环采用所提出的包含输入成形器、参考模型和自适应滑模控制的控制策略,电流环采用id=0的比例-积分(PI)控制策略[22]。由于在实际系统中电流环带宽远大于位置环带宽,在位置环的控制设计中,电流环的影响将被忽略。
|
| 图 2 基于本文控制策略的太阳能帆板驱动系统控制结构 Fig. 2 Control structure of SADS based on proposed control strategy |
本文的动机是通过输入成形器来抑制系统的柔性振动。然而,输入成形器是基于线性系统理论设计的,它不能直接应用于非线性系统。为了解决这个问题,本文提出了一个线性的参考模型,并利用自适应滑模控制使得太阳能帆板驱动系统的刚体子系统式(2)~式(3)表现得像这个线性的参考模型。因此,闭环的太阳能帆板驱动系统可以由这个线性的参考模型和线性的柔性体子系统式(4)来代表。也就是说,闭环的太阳能帆板驱动系统表现得像一个线性系统。在此基础上,输入成形器可以根据线性的参考模型和线性的柔性体子系统式(4)来设计。
2.1 参考模型设计由于在实际系统中耦合力矩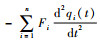
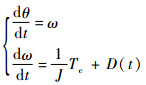
|
(6) |
式中:
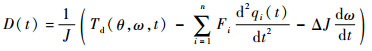
|
(7) |
对于实际系统,外界干扰力矩Td(θ, ω, t)和由转动惯量不确定引起的摄动项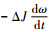
根据以上分析,针对标称系统
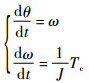
|
(8) |
设计如下比例-微分(PD)控制:
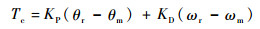
|
(9) |
式中:角速度指令ωr=0;KP为比例系数;KD为微分系数。将式(9)代入式(8),可以得到参考模型如下:
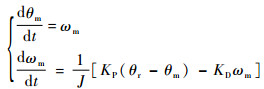
|
(10) |
为了抑制系统的柔性振动,本节针对闭环太阳能帆板驱动系统设计了输入成形器。
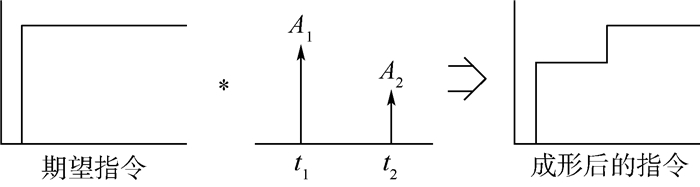
输入成形技术的基本原理如下[25]:将脉冲序列与任意的输入指令相卷积,所形成的新指令作为系统输入来控制系统的运动,如图 3所示。相比于原指令,所形成的新指令将引起更小的柔性振动。其中,脉冲序列称为输入成形器。
|
| 图 3 输入成形器原理图 Fig. 3 Schematic diagram of IS |
由于零振动(ZV)输入成形器具有结构简单的特点,本文采用考虑前两阶模态的具有4个时间脉冲的零振动输入成形器,其表达式如下[26]:
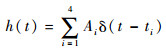
|
(11) |
式中:
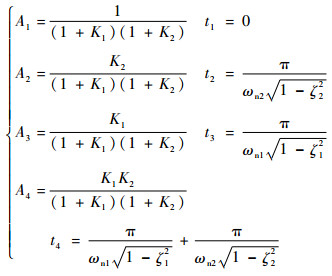
|
(12) |
其中:Ai和ti(i = 1, 2, 3, 4)分别为脉冲的幅值和作用时间;ωni和ζi(i=1, 2)分别为闭环太阳能帆板驱动系统的固有频率和阻尼比,并将在本节下文中推导。
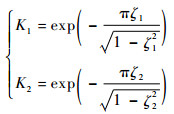
|
(13) |
由于刚体子系统式(2)~式(3)表现得像参考模型式(10),结合柔性体子系统式(4),闭环太阳能帆板驱动系统的运动方程可以表示为
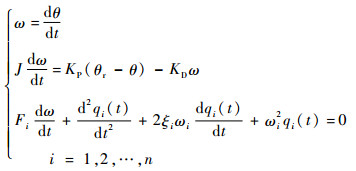
|
(14) |
由于在实际系统中,高阶模态不易被激发,因此通常对模态进行截断,本文将取系统前两阶模态(即n=2)进行研究。在此基础上,式(14)可以改写成形式如下的状态方程:
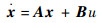
|
(15) |
式中:
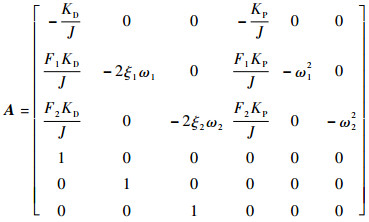
|
(16) |
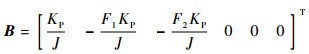
|
(17) |
状态向量为
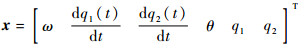
|
(18) |
输入为
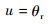
|
(19) |
根据式(16),可得矩阵A的复共轭特征值为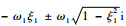
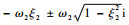
因此闭环系统式(14)的固有频率ωni=ωi,阻尼比ζi=ξi(i=1, 2)。
2.3 自适应滑模控制设计为了保证刚体子系统式(2)~式(3)表现得像参考模型式(10)并改善角位置控制性能,本节设计了自适应滑模控制。
首先,对系统作如下假设:
假设1 存在正常数D,使得D > |D(t)|。
定义角位置误差eθ=θm-θ和角速度误差eω=ωm-ω,并结合式(6)和式(10)可得
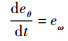
|
(20) |
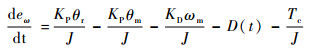
|
(21) |
定义滑模函数为
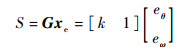
|
(22) |
式中:G=[k 1];xe=[eθ eω]T;k为正常数。
因此,自适应滑模控制可以设计为
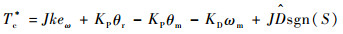
|
(23) |
式中: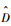
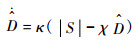
|
(24) |
其中:κ、χ均为正常数。根据式(24),易知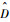
下面定理给出了所设计的自适应滑模控制对系统稳定性的影响。
定理1 考虑控制系统式(20)~式(21),在满足假设1的条件下,所设计的控制律式(23)~式(24)能够保证系统满足以下性能。
1) 一致有界:对于任意τ > 0,存在z(τ) < ∞,使得当‖σ(t0)‖≤τ时,对于任意t≥t0,‖σ(t)‖≤z(τ)。
2) 渐进一致有界:对于任意τ > 0,‖σ(t0)‖≤τ,存在z > 0,使得对于任意z > z,当t≥t0+T(z, τ),且T(z, τ) < ∞时,‖σ(t)‖≤z。
证明 本文利用Lyapunov minimax方法证明上述定理。
首先,选择控制系统的Lyapunov函数为
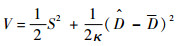
|
(25) |
对Lyapunov函数进行一次求导并代入式(20)~式(22),可得
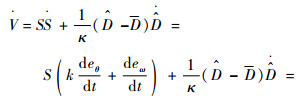
|
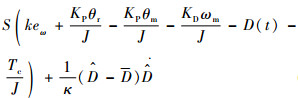
|
(26) |
将式(23)和式(24)代入式(26)可得
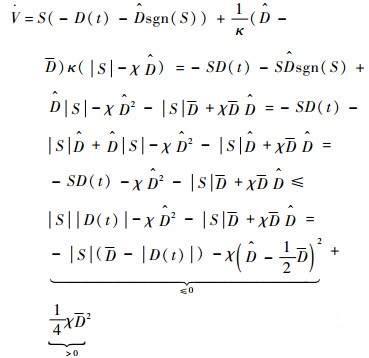
|
(27) |
根据式(27)和文献[27-28]的结论可知,eθ和eω是一致有界和渐进一致有界的。因此,本文所设计的自适应滑模控制律式(23)~式(24)可以保证系统式(20)~式(21)在不确定性影响下的一致有界性和渐进一致有界性。 证毕
需要指出的是,根据自适应律式(24)可知,当滑模函数S趋近于0,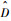
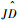
为了验证本文所提出的控制策略的有效性,本节以国际空间站的太阳能帆板驱动系统为例进行了数值仿真。系统的主要参数如表 1所示[29-30]。
| 参数 | 数值 |
| 定子电阻/Ω | 28 |
| 定子电感/H | 0.134 |
| 极对数 | 12 |
| 转矩常数/(N·m·A-1) | 9.22 |
| 额定电流/A | 1.4 |
| 额定功率/W | 22 |
| 传动比 | 325 |
| 最大静摩擦力矩/(N·m) | 404.54 |
| 第一阶模态耦合系数 | 188.7 |
| 第二阶模态耦合系数 | 30.1 |
| 第一阶模态阻尼比 | 0.01 |
| 第二阶模态阻尼比 | 0.01 |
| 第一阶模态角频率/(rad·s-1) | 1.789 |
| 第二阶模态角频率/(rad·s-1) | 11.21 |
| 转动惯量/(kg·m2) | 1.7×106 |
| 滑动摩擦力矩/(N·m) | 324.31 |
本文用振动能量衡量振动的强弱,并将其定义为
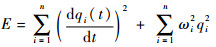
|
(28) |
假设外界干扰力矩Td(t)由随机干扰力矩Tr(t)和摩擦力矩Tf(t)构成,则
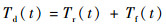
|
(29) |
式中:
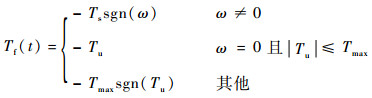
|
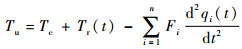
|
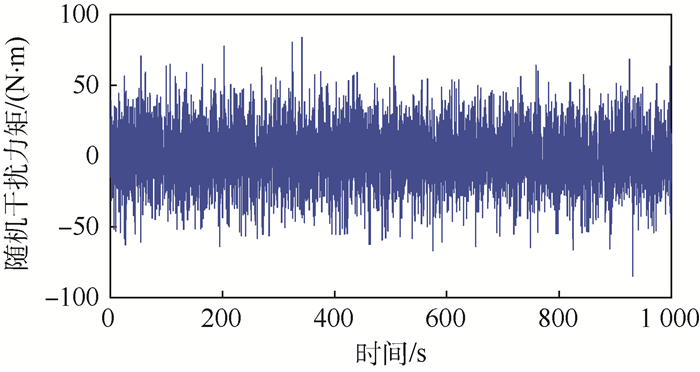
式中:Tu为作用在减速器输出轴上的主动力矩之和。根据表 1可知,最大静摩擦力矩Tmax为404.54 N·m,滑动摩擦力矩Ts为324.31 N·m。将随机干扰力矩Tr(t)的上界设为85 N·m[31]。此外,将转动惯量不确定性表示为
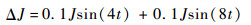
|
(30) |
为了说明本文所提控制策略的有效性,现对比例-积分-微分控制策略(PID)、自适应滑模控制策略、自适应滑模控制与输入成形相结合的控制策略这3种情况进行仿真。其中,PID控制采用位置-转速-电流三闭环控制结构,参数通过根轨迹方法设计;ASMC的参数通过经验选取;控制器参数如表 2所示。
| 控制器 | 参数 | 数值 |
| PID控制 | 比例系数(位置环) | 0.075 |
| 积分系数(位置环) | 0.000 8 | |
| 微分系数(位置环) | 2 | |
| 比例系数(速度环) | 33.3 | |
| 积分系数(速度环) | 0.1 | |
| 微分系数(速度环) | 0 | |
| 比例系数(电流环) | 500 | |
| 积分系数(电流环) | 6 000 | |
| 微分系数(电流环) | 0 | |
| ASMC | KP | 1 530 |
| KD | 89 760 | |
| k | 3 | |
| κ | 150 | |
| χ | 3 | |
| IS | A1 | 0.26 |
| A2 | 0.25 | |
| A3 | 0.25 | |
| A4 | 0.24 | |
| t1/s | 0 | |
| t2/s | 0.28 | |
| t3/s | 1.76 | |
| t4/s | 2.03 |
为了公平对比,电流环控制参数和随机干扰力矩Tr(t)波形(如图 4所示)在3种仿真情况中保持不变,3个控制器采样周期均设定为80 μs,系统的前向通道和反馈通道的时间延迟均设定为10 ms。
|
| 图 4 随机干扰力矩波形 Fig. 4 Random disturbance torque waveform |
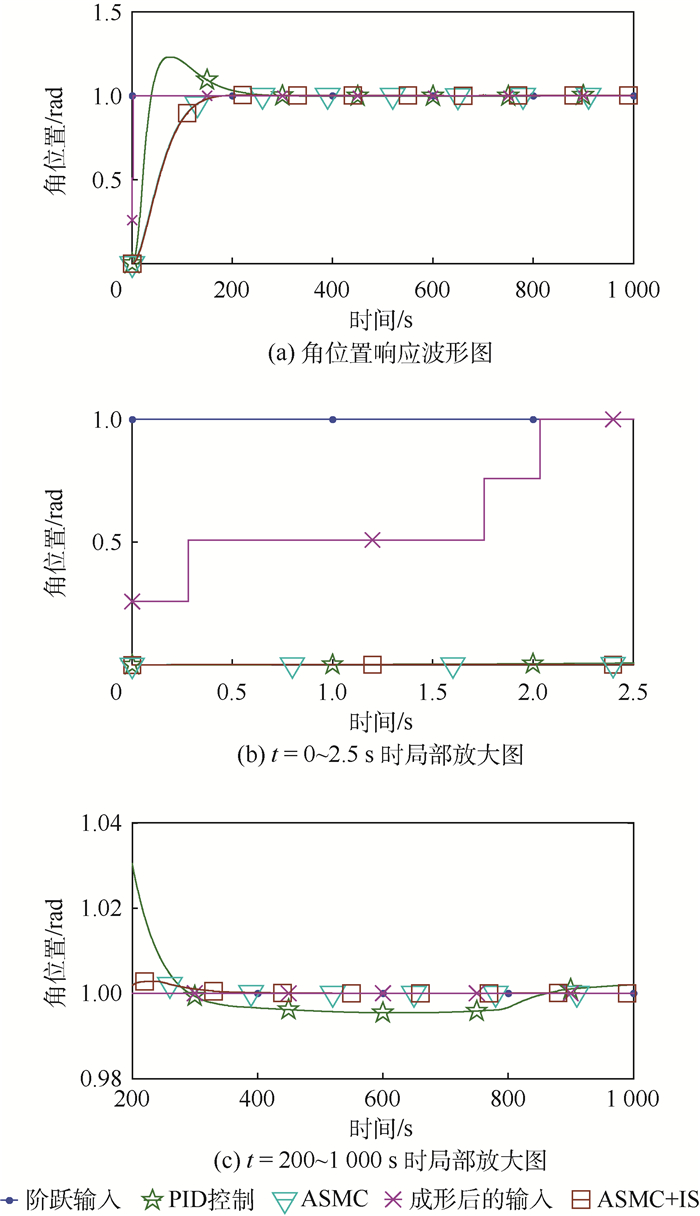
图 5为角位置阶跃给定情况下分别采用PID控制、ASMC和ASMC+IS时的位置响应波形图。由图 5可见,采用ASMC+IS时,系统调节时间为150.7 s,超调量为0.002 9 rad,超调过后,角位置轨线进入与位置指令最大偏差为0.000 1 rad的区域。采用ASMC时,超调量和最大偏差与采用ASMC+IS时相同,调节时间降低至149.6 s。采用PID控制时,调节时间和超调量分别为216.5s和0.23rad,当角位置轨线进入2%误差带后,轨线与位置指令最大偏差为0.004 5 rad。
|
| 图 5 角位置响应波形图及其局部放大图 Fig. 5 Oscillogram of time response of angular position and its partial enlarged views |
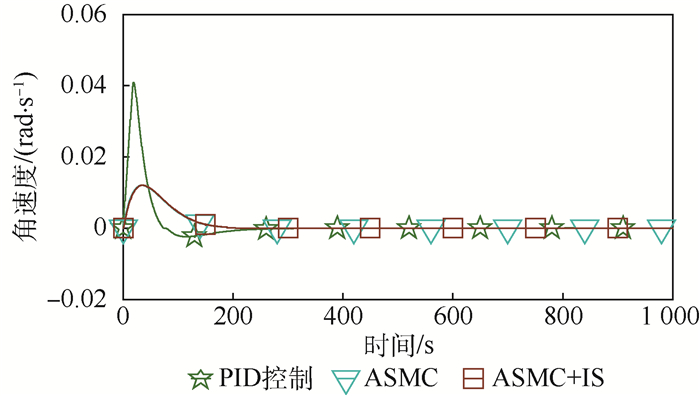
图 6为采用3种控制策略时的角速度响应波形图。由图 6可见,采用ASMC+IS时,转速峰值为0.012 rad/s;采用ASMC和PID控制时,转速峰值分别为0.012和0.041 rad/s。
|
| 图 6 角速度响应波形图 Fig. 6 Oscillogram of time response of angular velocity |
图 7为采用3种控制策略时的振动能量波形图。由图 7可见,采用ASMC+IS时,振动能量峰值为0.01 J;而采用ASMC和PID控制策略时,振动能量峰值分别为0.033和0.235 J。

|
| 图 7 振动能量波形图 Fig. 7 Oscillogram of vibration energy |
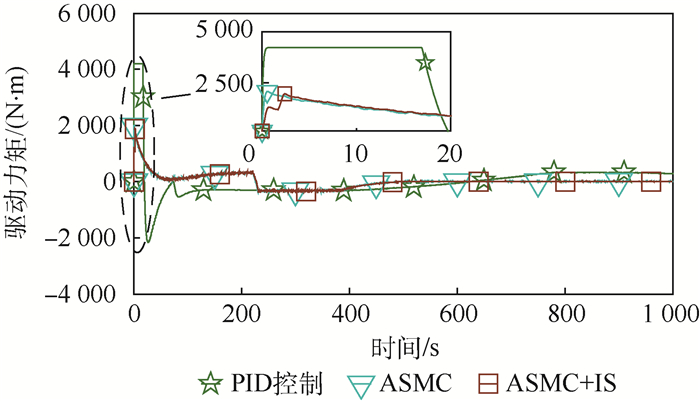
图 8为采用3种控制策略时的驱动力矩波形图。由图 8可见,采用ASMC+IS时,驱动力矩峰值为1 771 N·m;而采用ASMC和PID控制策略时,驱动力矩峰值分别为1 878和4 195 N·m。
|
| 图 8 驱动力矩波形图 Fig. 8 Oscillogram of driving torque |
综上可知,相比于PID控制,ASMC+IS有效改善了调节时间、超调量、跟踪误差、转速峰值和驱动力矩峰值,并将振动能量峰值降低了95.7%。因此,ASMC+IS比PID控制具有更强的角位置控制能力和振动抑制能力。相比于ASMC,ASMC+IS在超调量、跟踪误差和转速峰值方面具有相同的性能。尽管采用ASMC+IS时调节时间增加了0.67%,但是振动能量和驱动力矩峰值分别降低了69.7%和5.7%。因此,在角位置控制和振动抑制方面,ASMC+IS比ASMC具有更好的综合表现。
4 结论1) 为提高太阳能帆板驱动系统的角位置控制性能和抑制太阳能帆板的柔性振动,本文提出了一种自适应滑模控制与输入成形技术相结合的控制策略。
2) 理论分析表明,本文控制策略可以保证系统在不确定性影响下的一致有界性和渐进一致有界性。
3) 仿真结果表明,相比于PID控制,本文所提出的控制策略ASMC+IS在调节时间、超调量和跟踪误差方面具有更好的性能,并且降低了振动能量,有效抑制了柔性振动;相比于ASMC,ASMC+IS同样有效降低了振动能量,而其他性能基本相同。因此,ASMC+IS能在保证系统角位置控制性能的同时抑制太阳能帆板的柔性振动。
| [1] | JOSE S, GOPALAKRISHNAN E, TANGIRALA A K, et al. Stiffness control of cylindrical shells under axial compression using piezocomposite actuators-An experimental investigation[J]. Mechanics of Advanced Materials and Structures, 2017, 24 (1): 16–26. DOI:10.1080/15376494.2015.1091531 |
| [2] | SHIN C, HONG C, JEONG W B, et al. Active vibration control of plates using positive position feedback control with PZT actuators[J]. Noise Control Engineering Journal, 2016, 64 (2): 279–289. DOI:10.3397/1/376378 |
| [3] | OMIDI E, MAHMOODI S N. Novel hybrid positive feedback control for active vibration suppression in flexible structure[C]//2014 American Control Conference. Piscataway, NJ: IEEE Press, 2014: 2723-2728. |
| [4] | GASBARRI P, SABATINI M, LEONANGELI N, et al. Flexibility issues in discrete on-off actuated spacecraft:Numerical and experimental tests[J]. Acta Astronautica, 2014, 101 : 81–97. DOI:10.1016/j.actaastro.2014.04.012 |
| [5] | GASBARRI P, MONTI R, SABATINI M. Very large space structures:Non-linear control and robustness to structural uncertainties[J]. Acta Astronautica, 2014, 93 : 252–265. DOI:10.1016/j.actaastro.2013.07.022 |
| [6] | NA S, TANG G, CHEN L. Vibration reduction of flexible solar array during orbital maneuver[J]. Aircraft Engineering and Aerospace Technology, 2014, 86 (2): 155–164. DOI:10.1108/AEAT-05-2012-0072 |
| [7] | PAI M. Closed-loop input shaping control of vibration in flexible structures via adaptive sliding mode control[J]. Shock and Vibration, 2012, 19 (2): 221–233. DOI:10.1155/2012/803479 |
| [8] | SINGHOSE W, PORTER L, KENISON M, et al. Effects of hoisting on the input shaping control of gantry cranes[J]. Control Engineering Practice, 2000, 8 (10): 1159–1165. DOI:10.1016/S0967-0661(00)00054-X |
| [9] | SINGER N, SEERING W. Preshaping command inputs to reduce system vibration[M]. Cambridge: MIT Press, 1988: 76-82. |
| [10] | LU D, LIU Y. Singular formalism and admissible control of spacecraft with rotating flexible solar array[J]. Chinese Journal of Aeronautics, 2014, 27 (1): 136–144. DOI:10.1016/j.cja.2013.12.010 |
| [11] | LEE K W, SINGH S N. L1 adaptive control of flexible spacecraft despite disturbances[J]. Acta Astronautica, 2012, 80 : 24–35. DOI:10.1016/j.actaastro.2012.05.007 |
| [12] | HU Q. Robust adaptive attitude tracking control with L2-gain performance and vibration reduction of an orbiting flexible spacecraft[J]. Journal of Dynamic Systems, Measurement and Control, Transactions of the ASME, 2011, 133 (1): 011009. DOI:10.1115/1.4001703 |
| [13] | PUKDEBOON C. Adaptive-gain second-order sliding mode control of attitude tracking of flexible spacecraft[J]. Mathematical Problems in Engineering, 2014, 2014 (5): 693–697. |
| [14] | CHU M, CHEN G, JIA Q, et al. Simultaneous positioning and non-minimum phase vibration suppression of slewing flexible-link manipulator using only joint actuator[J]. Journal of Vibration and Control, 2014, 20 (10): 1488–1497. DOI:10.1177/1077546312470477 |
| [15] | ALIPOUR K, ZARAFSHAN P, EBRAHIMI A. Dynamics modeling and attitude control of a flexible space system with active stabilizers[J]. Nonlinear Dynamics, 2016, 84 (4): 2535–2545. DOI:10.1007/s11071-016-2663-y |
| [16] | PAI M. Discrete-time dynamic output feedback input shaping control of vibration in uncertain time-delay flexible structures[J]. Applied Mathematics and Computation, 2015, 250 : 675–688. DOI:10.1016/j.amc.2014.11.038 |
| [17] | PAI M. Robust input shaping control for multi-mode flexible structures using neuro-sliding mode output feedback control[J]. Journal of the Franklin Institute, 2012, 349 (3): 1283–1303. DOI:10.1016/j.jfranklin.2012.01.012 |
| [18] | HU Q. Robust adaptive sliding mode attitude control and vibration damping of flexible spacecraft subject to unknown disturbance and uncertainty[J]. Transactions of the Institute of Measurement and Control, 2012, 34 (4): 436–447. DOI:10.1177/0142331210394033 |
| [19] | XU W, MENG D, CHEN Y, et al. Dynamics modeling and analysis of a flexible-base space robot for capturing large flexible spacecraft[J]. Multibody System Dynamics, 2014, 32 (3): 357–401. DOI:10.1007/s11044-013-9389-0 |
| [20] |
白圣建, 黄新生. 快速机动大型挠性航天器的动力学建模[J].
航空学报, 2009, 30 (10): 1985–1992.
BAI S J, HUANG X S. Dynamic modeling of large flexible spacecraft undergoing fast maneuvering[J]. Acta Aeronautica et Astronautica Sinica, 2009, 30 (10): 1985–1992. DOI:10.3321/j.issn:1000-6893.2009.10.032 (in Chinese) |
| [21] | LI J, LI S, CHEN X. Adaptive speed control of a PMSM servo system using an RBFN disturbance observer[J]. Transactions of the Institute of Measurement and Control, 2012, 34 (5): 615–626. DOI:10.1177/0142331211410920 |
| [22] | LIU H, LI S. Speed control for PMSM servo system using predictive functional control and extended state observer[J]. IEEE Transactions on Industrial Electronics, 2012, 59 (2): 1171–1183. DOI:10.1109/TIE.2011.2162217 |
| [23] | LIANG H, SUN Z, WANG J. Robust decentralized attitude control of spacecraft formations under time-varying topologies, model uncertainties and disturbances[J]. Acta Astronautica, 2012, 81 (2): 445–455. DOI:10.1016/j.actaastro.2012.08.017 |
| [24] | WU S, RADICE G, GAO Y, et al. Quaternion-based finite time control for spacecraft attitude tracking[J]. Acta Astronautica, 2011, 69 (1-2): 48–58. DOI:10.1016/j.actaastro.2011.03.001 |
| [25] | HU Q. Input shaping and variable structure control for simultaneous precision positioning and vibration reduction of flexible spacecraft with saturation compensation[J]. Journal of Sound and Vibration, 2008, 318 (1-2): 18–35. DOI:10.1016/j.jsv.2008.03.068 |
| [26] | SUNG Y G, SINGHOSE W E. Robustness analysis of input shaping commands for two-mode flexible systems[J]. IET Control Theory and Applications, 2009, 3 (6): 722–730. DOI:10.1049/iet-cta.2007.0328 |
| [27] | CORLESS M J, LEITMANN G. Continuous state feedback guaranteeing uniform ultimate boundedness for uncertain dynamic systems[J]. IEEE Transactions on Automatic Control, 1981, 26 (5): 1139–1144. DOI:10.1109/TAC.1981.1102785 |
| [28] | IOANNO P A, KOKOTOVIC P V. Robust redesign of adaptive control[J]. IEEE Transactions on Automatic Control, 1984, 29 (3): 202–211. DOI:10.1109/TAC.1984.1103490 |
| [29] | LIM T W, COOPER P A, AYERS J K. Structural dynamic interaction with solar tracking control for evolutionary space station concepts[C]//Proceedings of the 33rd Structures, Structural Dynamics and Materials Conference. Reston: AIAA, 1992: 2108-2117. |
| [30] | BOUCHER R L. Mechanically induced g-jitter from space station rotary joints: JSC-CN-6110[R]. Washington, D. C. : NASA, 2000. |
| [31] | BOUCHER R L. Identification and mitigation of low frequency vibration sources on space station[C]//Dynamics Specialists Conference. Reston: AIAA, 1996: 451-462. |



