随着定位与导航技术的发展和普及,人们对基于位置服务(Location Based Service,LBS)的需求日益增加,尤其在大型商场、博物馆、超市、图书馆等复杂的室内环境中常常需要确定位置信息。研究高精度室内定位方法从而实现精确定位,在商业、社会公众服务、军事应用等方面具有广泛的应用。目前,室内定位系统主要分为2种:①基于蓝牙[1]、WiFi[2]、ZigBee[3]等各种无线网络的有源定位系统;②基于惯性传感器的无源定位系统[4]。基于各种无线网络的有源定位系统易受环境影响,在地震、火灾等突发事件发生时将不再适用。近年来,随着微机电系统(Micro-Electro-Mechanical System,MEMS)技术的发展,MEMS惯性测量单元(Inertial Measurement Unit,IMU)以其质量轻、体积小、功耗低且制造成本低等优点日益凸显[5]。基于脚部捷联MEMS-IMU的室内定位系统以其不受环境影响、定位精度高等优点逐步成为研究热点[6]。
由于惯性传感器本身存在漂移误差,尤其陀螺仪漂移率对惯性导航系统(Inertial Navigation System,INS)位置误差增长的影响是时间的三次方函数,而高精度的MEMS-IMU成本高昂,如何在节约成本的同时提高系统的定位精度是研究的难点。基于MEMS-IMU的室内定位系统框架INS+EKF+ZUPT方案[7]被提出,该方案首先引入零速修正(Zero-velocity Update,ZUPT)算法估计并校正器件的漂移误差,然后利用扩展卡尔曼滤波(Extended Kalman Filter,EKF)对INS[8]的解算结果进行修正。零速状态[9]的判定是ZUPT算法的基础,判定方法包括仅利用加速度信息或角速度信息进行独立判定[10],利用加速度和角速度信息进行联合判定[11],通过增加超声波[12]和磁力计[13]等辅助传感器进行判定等。为了降低成本,不增加额外传感器,同时充分利用现有传感器信息,本文ZUPT算法根据加速度计和陀螺仪输出的加速度和角速度信息对零速状态进行联合判定。传统ZUPT算法的零速判定阈值为固定值,一般根据室内行人最常见的运动模式即走(Walk)模式设定,可以有效修正器件累积误差[14]。但是当室内行人运动模式改变或增多时,如运动模式为静止(Still)、跑(Run)、上楼(Upstairs)或下楼(Downstairs)时,脚着地时间和方式不同,零速判定阈值也会改变,从而固定阈值将使包含多种运动模式的行人运动轨迹的定位精度下降。
随着模式识别理论研究的深入,基于惯性传感器的行人运动模式识别[15]具有运动数据获取自由、快捷等优点[16]。针对ZUPT算法零速判定阈值固定的缺陷,本文提出了一种多运动模式下自适应调整零速判定阈值的ZUPT算法。首先,对ZUPT算法原理进行了介绍;其次,论述了对室内行人包括静止、走、跑、上楼和下楼5种运动模式的零速判定阈值选取方法;然后,利用随机森林(Random Forest,RF)算法根据MEMS-IMU输出的加速度和角速度信息,实现对5种运动模式的识别;最后,实现了根据识别出的运动模式自适应调整ZUPT算法零速判定阈值。实验结果分析了不同条件下的算法性能,验证了其有效性。
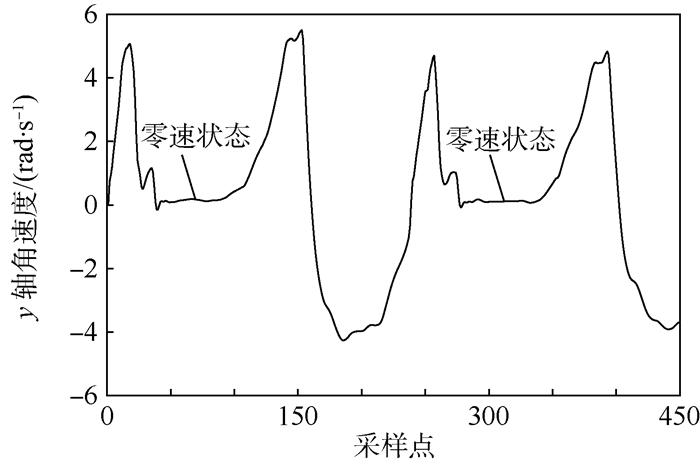
1 ZUPT算法 1.1 零速状态判定由于MEMS-IMU器件存在漂移误差,如果不进行校正,误差会随室内行人的行进过程逐渐积累,导致定位结果发散。因此,定位算法常引入ZUPT算法修正器件的累积误差。理论上,如果行人捷联MEMS-IMU的脚在落地的短时间内,速度和角速度为零,此段时间即为零速状态。ZUPT算法执行的核心是判定零速状态及其对应时刻。图 1为室内行人最常见的走运动模式下截取部分y轴角速度的变化。
|
| 图 1 y轴角速度变化 Fig. 1 Angular velocity variation of y axis |
由图 1可知,脚与地刚开始接触到脚再次离地时的角速度变化是指在零值附近且比较平稳的一段,即零速状态。然而,由于传感器的量测误差、噪声以及算法本身存在的误差等,此时速度计算值和陀螺仪的角速度输出值并不为零。本文选用根据加速度信息和角速度信息联合判定的方法对零速状态时刻进行判定。k时刻零速判定公式[17]为
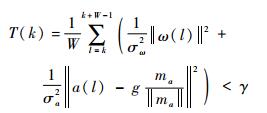
|
(1) |
式中:T(k)为k时刻加速度和角速度的函数;γ为零速判定阈值;W为时间窗的宽度;σω为角速度测量误差标准差;σa为加速度测量误差标准差;g为重力加速度;ω(l)和a(l)分别为时间窗内l时刻的角速度和加速度值;||·||为2-范数;ma为时间窗内所有样本的加速度平均值,计算公式如下:
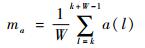
|
(2) |
通常情况下,当k时刻的加速度和角速度信息满足式(1)时,则判定k时刻为零速状态。
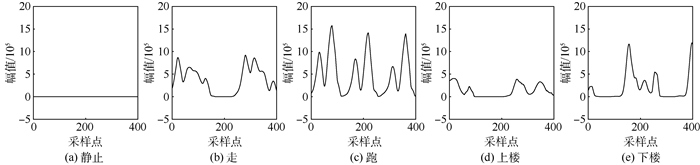
1.2 零速判定阈值选取零速判定阈值γ的正确选取是能否正确判定零速状态的关键,目前常用的方法是固定阈值法,即根据某种运动模式对应的T(k),使用多组实验数据验证,选取定位精度最高时的对应阈值作为ZUPT算法零速判定阈值。图 2给出了静止、走、跑、上楼和下楼5种运动模式下的T(k)变化。
|
| 图 2 5种运动模式T(k)变化 Fig. 2 T(k) variation of five movement patterns |
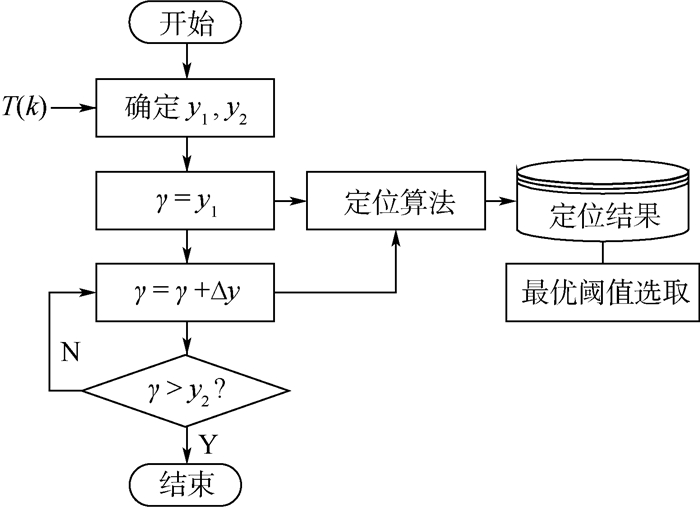
由图 2可知,不同运动模式下的T(k)幅值变化曲线有明显区别,每种运动模式对应的T(k)都是周期循环变化的,每个周期对应一次完整的步态,每个周期内的最低点附近对应的时刻即为零速状态时刻。静止运动模式下,T(k)在零值以上微小波动,零速判定阈值γ只要高于该值即可。对于其他4种运动模式,每个步态周期内,T(k)都有一个最低点和一个次最低点,零速判定阈值γ的选取应该位于最低点纵坐标值y1和次最低点纵坐标值y2之间。由于行人运动的随机性,每个步态周期输出的加速度和角速度数值会有一定的差异性,所以T(k)在每个步态周期内的大小也具有差异性,每个步态最低点和次最低点对应纵坐标值不同,零速判定阈值γ应满足y2 < γ < y1。由以上可知,不同运动模式下的零速判定阈值γ大小不同,并不是固定值,当运动轨迹包含多种运动模式时,固定阈值将造成零速状态的误判,导致定位结果严重发散。为了确定走、跑、上楼和下楼4种运动模式对应的零速判定阈值γ,采用遍历的方法从(y2, y1)区间中选取出最优阈值,零速判定阈值选取流程如图 3所示。
|
| 图 3 零速判定阈值选取流程 Fig. 3 Flowchart of zero-velocity determination threshold selection |
由图 3可知,各运动模式零速判定阈值选取的方法如下:首先,根据T(k)确定最低点和次最低点对应纵坐标值y1和y2;然后,将零速判定阈值γ从y1至y2以Δy为间隔依次遍历,并依次输入给定位算法,得到定位结果;最后,选取最优定位结果对应的阈值作为该模式零速判定阈值,实现阈值的选取。
2 多运动模式下阈值自适应调整 2.1 运动模式识别算法在室内环境中,行人常见的运动模式有静止、走、跑、上楼和下楼5种。行人运动模式识别是利用MEMS-IMU采集的加速度和角速度信息来训练机器学习模型,然后对在线数据信息进行分类识别的过程[18]。该算法主要包括原始数据采集、数据预处理、特征向量提取、分类识别4个步骤。行人运动模式识别算法的总体流程如图 4所示。

|
| 图 4 行人运动模式识别算法流程 Fig. 4 Flowchart of pedestrian movement pattern recognition algorithm |
利用MEMS-IMU集成的三轴加速度计、三轴陀螺仪以固定的采样频率采集数据信息,得到下列原始数据:三轴加速度(ax、ay、az)、三轴角速度(ωx、ωy、ωz)。
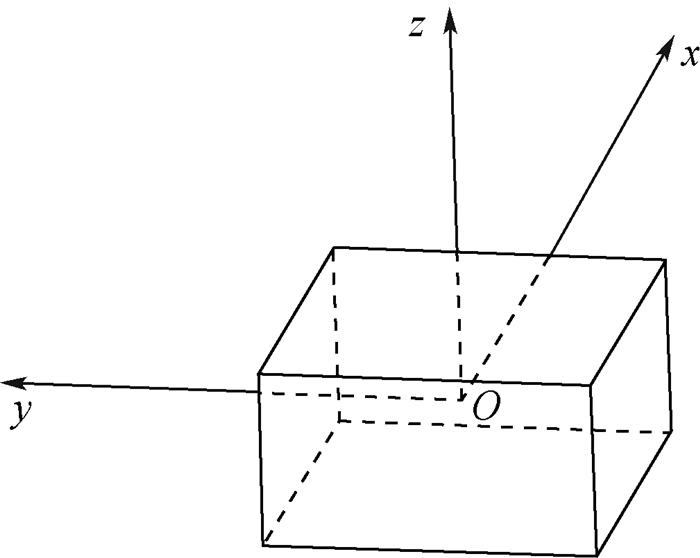
采集过程中,坐标系的定义如图 5所示,满足右手螺旋法则。
|
| 图 5 坐标系定义 Fig. 5 Definition of coordinate system |
由于采集数据时人为启动和关闭设备会造成其抖动,数据采集过程中存在噪声,影响数据采集质量,利用平滑滤波及加窗方法对原始数据进行预处理,得到如式(3)所示的有用数据:
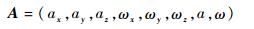
|
(3) |
式中:
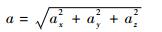
|
(4) |
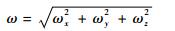
|
(5) |
A为原始数据经预处理后的矩阵。a和ω为三轴加速度(ax、ay、az)和三轴角速度(ωx、ωy、ωz)的合成加速度和合成角速度。
2.1.2 特征向量提取为了对5种行人运动模式进行分类识别,需要从预处理后的数据中提取特征向量。利用加窗的方法,对数据进行分组,并对每组数据分别求取特征向量[19]。
假设s1, s2, …, sN为A中某一惯性参数的样本数据,N为样本个数,则特征向量为
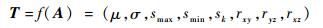
|
(6) |
式中:T为特征向量;f(A)为矩阵A的函数;μ为样本算数平均值,且
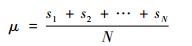
|
(7) |
σ为样本标准差,且
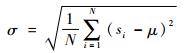
|
(8) |
smax为样本最大值,且
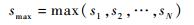
|
(9) |
smin为样本最小值,且
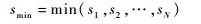
|
(10) |
sk为样本偏度,且
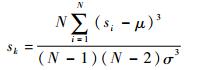
|
(11) |
rxy为样本x轴和y轴数据之间的相关系数,且
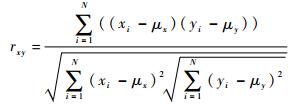
|
(12) |
ryz为样本y轴和z轴数据之间的相关系数,且
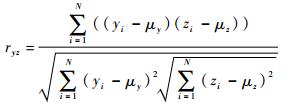
|
(13) |
rxz为样本x轴和z轴数据之间的相关系数,且
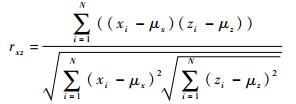
|
(14) |
其中:xi、yi和zi分别为x轴、y轴和z轴数据;μx、μy和μz分别为x轴、y轴和z轴数据的算术平均值。
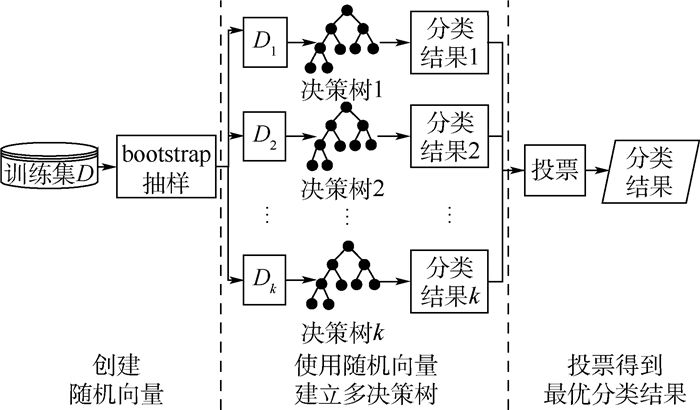
2.1.3 分类识别机器学习在数据挖掘、模式识别、计算机视觉等许多领域都有广泛应用。RF算法[20]是一种可以有效解决分类问题的机器学习算法,引入2个随机性,具有很好的抗噪声能力,并且具有较快的学习速度,变量重要性度量可以作为高维数据的特征选择工具。近年来,RF算法已经被广泛应用于各种分类预测特征选择以及异常点检测问题中。RF算法定义为一个由一组决策树分类器{h(X, θk), k=1, 2, …, ntree}组成的集成分类器,{θk}为服从独立同分布的随机向量,ntree为RF算法中决策树的个数,在给定自变量X下,每个决策树分类器通过投票来决定最优的分类结果。RF算法原理示意图如图 6所示。
|
| 图 6 RF算法原理示意图 Fig. 6 Schematic of RF algorithm |
由图 6可知,RF算法基本原理主要分为3个步骤:
步骤1 创建随机向量。利用bootstrap随机重采样方法从原始训练集抽取k个样本,且每个样本的样本容量都与原始训练集一样,得到k个随机向量。
步骤2 使用随机向量建立多决策树。对k个随机向量分别建立k个决策树模型,并得到k种分类结果。
步骤3 投票得到最优分类结果。根据k种分类结果对每个记录进行投票表决,决定其最终分类。
利用RF算法对5种运动模式的特征向量进行分类识别,选取决策树个数ntree=100。将离线采集的数据提取的特征向量作为训练集,训练模型;将在线采集的数据提取的特征向量作为测试集,输入模型即可得到识别结果。
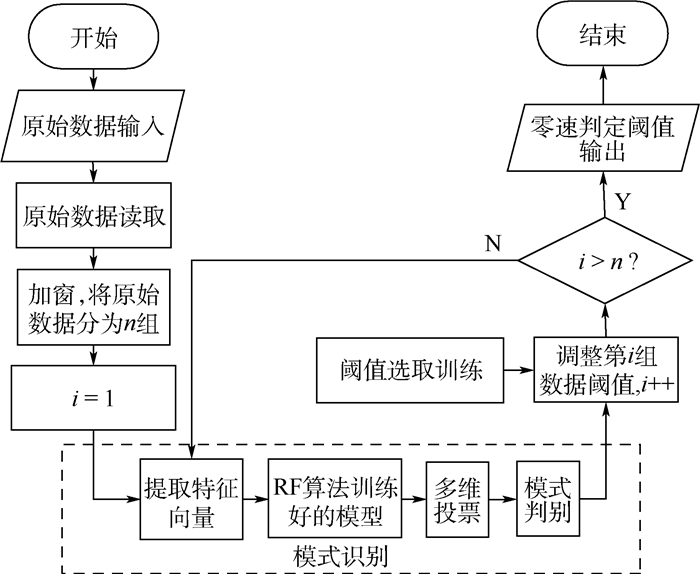
2.2 ZUPT算法阈值自适应调整在得到5种运动模式对应的零速判定阈值和识别结果后,为了提高定位精度,对包含多种运动模式的室内行人运动轨迹实现零速判定阈值γ的自适应调整,需要将运动模式识别算法与ZUPT算法进行融合。阈值自适应调整算法流程如图 7所示。
|
| 图 7 阈值自适应调整算法流程 Fig. 7 Flowchart of threshold adaptive adjustment algorithm |
由图 7可知,阈值自适应调整算法的基本原理主要分为以下步骤:
步骤1 输入并读取室内行人一段运动轨迹采集的原始加速度和角速度数据。
步骤2 对原始数据进行加窗,将数据分割为n组。
步骤3 对第i组数据进行特征向量提取,并作为测试集输入到RF算法训练好的模型中,得到每个特征向量对应的运动模式。
步骤4 将得到的多个运动模式识别结果进行多维投票,得到该组数据的判别模式。
步骤5 结合5种运动模式阈值训练选取模块输出的5种运动模式的零速判定阈值,将该段时间内的ZUPT算法零速判定阈值调整为判别模式所对应阈值,同时将i值增1。
步骤6 循环整个过程直到i>n,即n组数据都完成模式识别并自适应调整零速判定阈值,输出所有零速判定阈值。
3 实验与结果分析 3.1 数据采集为了验证本文算法的可行性和有效性,需要利用MEMS-IMU采集加速度和角速度数据信息,考虑定位精度和设备体积,选择Inertial Labs公司的AHRS-1微机电惯性测量单元进行数据采集,并为了降低设备抖动,将AHRS-1安装在消防靴底部。AHRS-1集成的三轴加速度计、陀螺仪参数如表 1所示。
| 传感器 | 参数 | 指标 |
| 加速度计 | 采样率/Hz | 200 |
| 量程/g | 6 | |
| 零偏稳定性/μg | 50 | |
| 分辨率/mg | 0.1 | |
| 陀螺仪 | 采样率/Hz | 200 |
| 量程/((°)·s-1) | 500 | |
| 零偏稳定性/((°)·h-1) | 4 | |
| 分辨率/((°)·s-1) | 0.01 |
利用该惯性测量单元采集静止、走、跑、上楼和下楼5种运动模式的三轴加速度和三轴角速度信息,加速度大小都在[-6 g,6 g]范围内,角速度大小都在[-500, 500](°)/s范围内,满足数据的采集需求。
为了利用RF算法训练模式识别模型并测试其识别效果,同时确定每种运动模式对应的零速判定阈值γ,在北京航空航天大学新主楼内进行多组数据采集,对静止、走、跑、上楼和下楼5种运动模式分别采集10 min。
为了验证本文所提出的多运动模式下自适应阈值ZUPT算法对定位精度的影响,在北京航空航天大学新主楼内进行了3组实验,同时为了说明统计效果,对包含5种运动模式的实验3采集了3组数据,采集方式如表 2所示。
| 实验 | 运动方式 |
| 实验1 | 常速跑步,采集2 min;运动轨迹闭合 |
| 实验2 | 依次常速走路, 常速跑步, 共采集5 min;运动轨迹闭合 |
| 实验3 | 依次常速走路, 常速上楼, 静止站立, 常速下楼, 常速跑步, 共采集12 min;运动轨迹闭合;采集3组 |
3.2 算法验证 3.2.1 运动模式识别算法验证及阈值选取
为了验证RF算法对5种运动模式的识别效果,对采集的5种运动模式的原始数据经过数据预处理和特征向量提取,得到5种运动模式的特征向量,从每种模式的特征向量中随机选取363组构成数据集。为了充分利用数据集对算法效果进行测试,采用10-折交叉验证(10-fold cross validation),即将数据集随机分成10份,每次选取1份作为测试集,其余9份作为训练集,采用RF算法进行分类识别,算法识别率如表 3所示。
| 测试 | 10-折交叉 | 识别率/% |
| Test1 | 171/171 | 100 |
| Test2 | 178/179 | 99.44 |
| Test3 | 169/169 | 100 |
| Test4 | 181/181 | 100 |
| Test5 | 164/164 | 100 |
| Test6 | 200/200 | 100 |
| Test7 | 204/204 | 100 |
| Test8 | 182/182 | 100 |
| Test9 | 188/188 | 100 |
| Test10 | 177/177 | 100 |
根据表 3中10-折交叉验证结果,将10次测试识别率的平均值作为总识别率,可得总识别率为99.94%。说明该运动模式识别算法可以用于识别室内行人的运动模式,进而根据识别结果自适应调整ZUPT算法的零速判定阈值。
在正确识别5种运动模式后,对5种运动模式采集的多组数据进行分析,选取最优定位结果对应阈值作为零速判定阈值,得到各运动模式阈值选取值如表 4所示。
| 模式 | 阈值 |
| 静止 | 400 |
| 走 | 25 000 |
| 跑 | 40 000 |
| 上楼 | 4 000 |
| 下楼 | 5 000 |
5种运动模式T(k)与零速判定阈值γ比较如图 8所示。

|
| 图 8 5种运动模式T(k)与γ比较 Fig. 8 Comparison of five movement patterns'T(k) and γ |
图 8(a)为5种运动模式T(k)与对应零速判定阈值γ对比,图 8(b)为零速状态阶段5种运动模式T(k)与对应零速判定阈值γ对比。可知,选取表 4中5种运动模式的零速判定阈值都高于T(k)最低点且低于次最低点,可以正确判定各运动模式室内行人零速状态。
3.2.2 阈值自适应调整验证对于3组包含不同运动模式的实验,利用原始数据识别运动模式并自适应调整零速判定阈值,MATLAB软件平台下自适应调整ZUPT阈值和传统固定ZUPT阈值的比较结果如图 9所示。
|
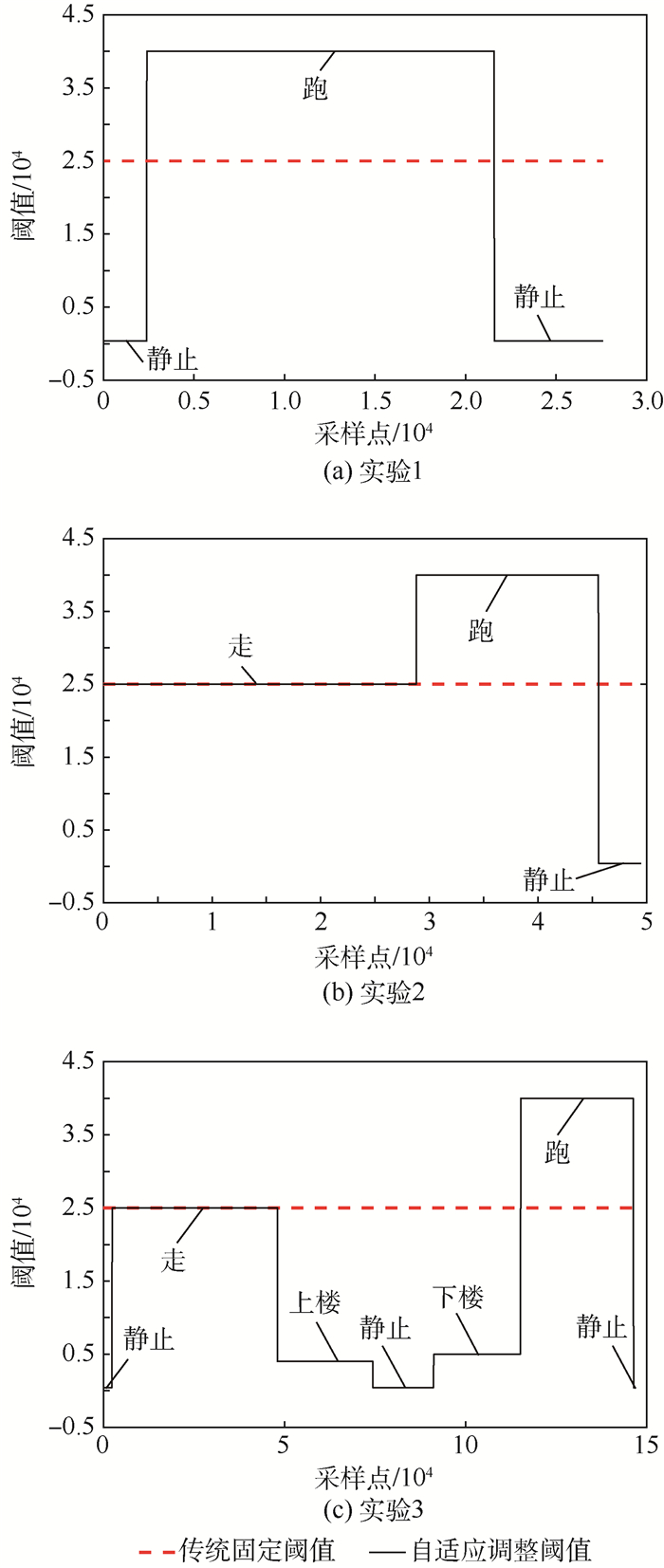
| 图 9 自适应调整阈值与固定阈值变化比较 Fig. 9 Variation comparison of adaptively adjusted threshold and fixed threshold |
图 9(a)为实验1自适应调整ZUPT阈值与传统固定ZUPT阈值对比,可知,与固定阈值的ZUPT算法相比,多运动模式下的自适应调整阈值的ZUPT算法将室内行人的运动模式识别为跑运动模式,以及设备启动后和关闭前短时间的静止运动模式,并根据识别结果自适应将阈值进行了相应调整。
图 9(b)为实验2自适应调整ZUPT阈值与传统固定ZUPT阈值对比,可知,与固定阈值的ZUPT算法相比,多运动模式下自适应调整阈值的ZUPT算法将室内行人的运动模式依次识别为走运动模式、跑运动模式,和设备关闭前短时间的静止运动模式,并根据识别结果自适应将阈值进行了相应调整。
图 9(c)为实验3第1组实验自适应调整ZUPT阈值与传统固定ZUPT阈值对比,可知,与固定阈值的ZUPT算法相比,多运动模式下自适应调整阈值的ZUPT算法将室内行人的运动模式依次识别为走运动模式、上楼运动模式、静止运动模式、下楼运动模式、跑运动模式,以及设备启动后和关闭前短时间的静止运动模式,并根据识别结果自适应将阈值进行了相应调整。
由图 9中ZUPT零速判定阈值自适应调整结果可知,3组实验的运动模式识别结果与实验数据采集过程的实际运动模式相吻合。
3.2.3 定位结果分析以包含5种运动模式的实验3第1组实验为例,引入本文多运动模式下自适应调整零速判定阈值的ZUPT算法与引入传统固定阈值ZUPT算法后,定位算法的平面定位结果在MATLAB软件平台下的仿真对比如图 10所示。
|
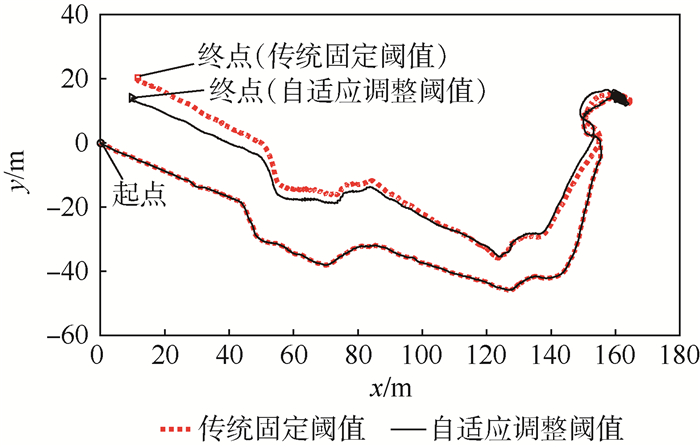
| 图 10 实验3平面定位结果比较 Fig. 10 Comparison of plane positioning results of Experiment 3 |
由图 10可知,由于自适应调整阈值的ZUPT算法将第1段时间内的运动模式识别为走运动模式,并将阈值自适应调整为走运动模式对应阈值,此阈值与传统固定阈值算法的阈值相同,所以该段时间内2种算法的定位结果相同。因此,引入多运动模式下自适应调整阈值的ZUPT算法主要是对走运动模式之后的上楼运动模式、静止运动模式、下楼运动模式和跑运动模式对应的阈值进行自适应调整,实现了对定位结果的修正,由图 10中2种定位算法定位结果的终点位置可知,定位误差减小。
为了说明本文提出的自适应调整零速判定阈值的ZUPT算法对定位精度的影响,引入行走总距离误差(Total Traveled Distance Error, TTDE)[6],即闭环运动轨迹下最终定位误差与行走总距离之比。多运动模式下自适应调整零速判定阈值的ZUPT算法与传统固定阈值的ZUPT算法后的TTDE对比如表 5所示。
| % | ||||||
| 误差 | 实验1 | 实验2 | 实验3 | |||
| 1 | 2 | 3 | 平均 | |||
| TTDE (传统固定阈值) |
6.19 | 10.60 | 4.39 | 5.41 | 3.76 | 4.52 |
| TTDE (自适应调整阈值) |
1.62 | 4.43 | 3.15 | 3.68 | 2.74 | 3.19 |
| 精度提升 | 73.83 | 58.21 | 28.25 | 31.98 | 27.13 | 29.12 |
由表 5可知,识别运动模式并自适应调整零速判定阈值的ZUPT算法可以使包含多种运动模式的3组实验行走总距离误差TTDE减小,定位精度显著提升。对于跑运动模式占比较大的实验1和实验2,固定阈值下二者行走总距离误差TTDE都较大,而本文提出的多运动模式下自适应阈值ZUPT算法可以使定位精度相应提升73.83%和58.21%。对于包含5种运动模式的实验3,3组实验统计平均的定位精度提升29.12%。
4 结论本文在传统ZUPT算法零速判定阈值固定的基础上,分析并选取静止、走、跑、上楼或下楼5种运动模式的零速判定阈值,并对室内行人运动模式进行分类识别,进而提出了多运动模式下自适应阈值ZUPT算法。经实验验证表明:
1) 实现了静止、走、跑、上楼或下楼5种运动模式的正确识别,采用10-折交叉验证,5种运动模式的总识别率达到99.94%。
2) 针对静止、走、跑、上楼或下楼5种运动模式,实现了最优零速阈值的选取。
3) 进行了3组包含多运动模式的实验,定位精度最好可提升73.83%。
本文提出的算法扩展了传统基于MEMS-IMU的惯性导航系统的适用范围,并提高了定位精度。
| [1] | BEKKELIEN A. Bluetooth indoor positioning[D]. Geneva: University of Geneva, 2012: 11-25. |
| [2] | YANG C, SHAO H R. WiFi-based indoor positioning[J]. IEEE Communications Magazine, 2015, 53 (3): 150–157. DOI:10.1109/MCOM.2015.7060497 |
| [3] |
李尧, 汪明, 于晓谕. 基于ZigBee室内定位算法[J].
计算机系统应用, 2016, 25 (6): 180–184.
LI Y, WANG M, YU X Y. Indoor location algorithm based on ZigBee[J]. Computer Systems & Applications, 2016, 25 (6): 180–184. (in Chinese) |
| [4] | FISCHER C, SUKUMAR P T, HAZAS M. Tutorial:Implementing a pedestrian tracker using inertial sensors[J]. IEEE Pervasive Computing, 2013, 12 (2): 17–27. DOI:10.1109/MPRV.2012.16 |
| [5] | MONTORSI F, PANCALDI F, VITETTA G M. Design and implementation of an inertial navigation system for pedestrians based on a low-cost MEMS IMU[C]//IEEE International Conference on Communications Workshops. Piscataway, NJ: IEEE Press, 2015: 57-61. |
| [6] | ZHENG X, YANG H, TANG W, et al. Indoor pedestrian navigation with shoe-mounted inertial sensors[M]//PARK J J, CHEN S C, GIL J M, et al. Multimedia and ubiquitous engineering. Berlin: Springer, 2014: 67-73. |
| [7] | JIMÉNEZ A R, SECO F, PRIETO J C, et al. Indoor pedestrian navigation using an INS/EKF framework for yaw drift reduction and a foot-mounted IMU[C]//20107th Workshop on Position-ing Navigation and Communication (WPNC). Piscataway, NJ: IEEE Press, 2010: 135-143. |
| [8] |
张华强, 赵剡, 陈雨. 捷联惯性导航系统整体标定新方法[J].
北京航空航天大学学报, 2012, 38 (4): 459–463.
ZHANG H Q, ZHAO Y, CHEN Y. New system calibration method for strapdown inertial navigation system[J]. Journal of Beijing University of Aeronautics and Astronautics, 2012, 38 (4): 459–463. (in Chinese) |
| [9] | ALTUN K, BARSHAN B. Pedestrian dead reckoning employing simultaneous activity recognitioncues[J]. Measurement Science and Technology, 2012, 23 (2): 25103. DOI:10.1088/0957-0233/23/2/025103 |
| [10] |
唐文杰, 吕志伟, 张伦东, 等. 基于零速修正辅助MIMU的行人导航算法研究[J].
大地测量与地球动力学, 2016, 36 (6): 548–551.
TANG W J, LÜ Z W, ZHANG L D, et al. Research of pedestrian navigation algoritm based on zero velocity update aided MIMU[J]. Journal of Geodesy and Geodynamics, 2016, 36 (6): 548–551. (in Chinese) |
| [11] | SKOG I, HÄNDEL P, NILSSON J O, et al. Zero-velocity detection-An algorithm evaluation[J]. IEEE Transactions on Biomedical Engineering, 2010, 57 (11): 2657–2666. DOI:10.1109/TBME.2010.2060723 |
| [12] |
李辰祥. 基于MEMS行人惯性导航的零速度修正技术研究[D]. 厦门: 厦门大学, 2014.
LI C X. Research on zero-velocity update technology of pedestrian inertial navigation based on MEMS[D]. Xiamen: Xiamen University, 2014(in Chinese). http://dspace.xmu.edu.cn/handle/2288/84427?locale-attribute=zh |
| [13] |
李佳璇. 双MIMU/磁力计单兵导航技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2015.
LI J X. Research on dual MIMU/magnetometer technology of pedestrian navigation system[D]. Harbin: Harbin Engineering University, 2015(in Chinese). |
| [14] | WANG Z, ZHAO H, QIU S, et al. Stance-phase detection for ZUPT-aided foot-mounted pedestrian navigation system[J]. IEEE/ASME Transactions on Mechatronics, 2015, 20 (6): 3170–3181. DOI:10.1109/TMECH.2015.2430357 |
| [15] |
路永乐, 张欣, 龚爽, 等. 基于MEMS惯性传感器的人体多运动模式识别[J].
中国惯性技术学报, 2016, 24 (5): 589–594.
LU Y L, ZHANG X, GONG S, et al. Recognition of multiple human motion patterns based on MEMS inertial sensors[J]. Journal of Chinese Inertial Technology, 2016, 24 (5): 589–594. (in Chinese) |
| [16] |
薛洋. 基于单个加速度传感器的人体运动模式识别[D]. 广州: 华南理工大学, 2011.
XUE Y. Human motion patterns recognition based on single triaxial accelerometer[D]. Guangzhou: South China University of Technology, 2011(in Chinese). |
| [17] | NILSSON J O, SKOG I, HÄNDEL P, et al. Foot-mounted INS for everybody-An open-source embedded implementation[C]//2012 IEEE/ION Position Location and Navigation Symposium (PLANS). Piscataway, NJ: IEEE Press, 2012: 140-145. |
| [18] | INCEL O D, KOSE M, ERSOY C. A review and taxonomy of activity recognition on mobile phones[J]. Bionanoscience, 2013, 3 (2): 145–171. DOI:10.1007/s12668-013-0088-3 |
| [19] |
张健敏, 修春娣, 杨威, 等. 基于Android手机的用户行为模式识别算法[C]//全国信号和智能信息处理与应用学术会议, 2016: 463-468.
ZHANG J M, XIU C D, YANG W, et al. User's behavior pattern recognition algorithm based on Android phones[C]//National Signal and Intelligent Information Processing and Application Academic Conference, 2016: 463-468(in Chinese). |
| [20] |
方匡南, 吴见彬, 朱建平, 等. 随机森林方法研究综述[J].
统计与信息论坛, 2011, 26 (3): 32–38.
FANG K N, WU J B, ZHU J P, et al. A review of technologies on random forests[J]. Statistics & Information Forum, 2011, 26 (3): 32–38. (in Chinese) |



