工程优化设计是以产品结构为基础,根据设计要求、产品功能等,结合现代优化技术,在可行域中搜索最优设计方案,以达到缩短设计周期、提高产品质量和降低生产成本的目的。目前的结构优化设计方法大致可以分为两大类:基于梯度的优化设计方法和随机优化设计方法。前者利用梯度信息从初值点逐渐向最优值点搜索[1];后者则是研究人员受自然现象、动物行为和人类社会等启发而建立的。但是实际工程中的结构优化设计问题,往往拥有较多的设计变量和约束条件,目标函数和约束条件也比较复杂,此时第一类方法的可行性与准确性受到了极大地考验,而随机优化设计方法则可以很大程度地弥补这一不足。随着计算机性能的不断提高,随机优化设计方法更加受科研人员青睐。
交叉熵(Cross Entropy, CE)方法是一种可靠性分析与随机优化设计的统一方法,其基本概念由Rubinstein[2]于1997年最先提出并用于模拟稀疏事件。随后Rubinstein又将其拓展为随机优化设计方法[3]。之后,国内外众多科研人员对交叉熵方法进行了详细地研究与改进。2001年,Helvik和Wittner[4]在原有交叉熵方法的基础之上做出改进,使其运用于含有多个相互独立的智能主体网络的路径寻找问题,结果证明交叉熵方法拥有很好的收敛性,并且能够得出理想的优化结果。2005年,Alon等[5]采用交叉熵方法优化缓冲区分配问题,基于交叉熵的优化方法计算效率高,优化结果与理论值的误差不超过1%的概率大约为99%。同年,Kuo等[6]采用交叉熵方法处理车辆路径优化问题并得到了令人满意的结果,证明了交叉熵方法在解决这类问题时,对不同的目标函数和约束条件都有很好的效果,并且针对各类具体问题(尤其是车辆路径问题)都能得出很好的优化结果。2006年,Kroese等[7]针对多极值和非线性约束的连续优化问题,提出了改进的交叉熵方法。2010年,Ho和Yang[8]使用交叉熵优化方法处理电磁场中的逆问题,引入变异操作增强了算法的全局搜索能力。2014年,丁卫平等[9]将交叉熵方法与混合蛙跳算法相结合,处理MRI (Magnetic Resonance Images)图像分割问题,改善了原始算法的计算精度。同年,李国成和肖庆宪[10]利用交叉熵方法改进蝙蝠算法,降低了原始算法陷入局部最优的概率,并验证了该方法处理高维优化问题的可行性。2015年,Ghidey[11]对交叉熵方法在可靠性优化设计问题中的精度和效率进行了详细的研究,结果表明相比于解析方法和现有的可靠性优化方法,交叉熵方法在精度和效率上都具有一定的优势。这些研究成果表明将交叉熵方法和其他优化方法相结合,具有很大的发展潜力和应用前景。但总体而言,目前国内外对基于交叉熵的可靠性分析与随机优化设计方法的研究还少见诸于公开发表文献。所以,作为一种新兴的、高效的可靠性分析与随机优化的统一方法,交叉熵方法值得深入探索和研究。本文着眼于交叉熵方法在随机优化问题中的应用,详细分析传统交叉熵方法在处理优化问题时的优缺点,尝试从参数更新策略、平滑参数调整和变异操作3个方面作出改进,并利用2个数值算例和1个工程算例验证改进交叉熵方法的效率、精度和鲁棒性。
1 传统交叉熵方法交叉熵定义为2个概率密度函数比值对数的期望:
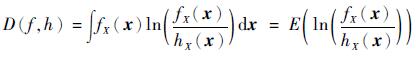
|
(1) |
式中:E(·)为期望算子;x为n维随机输入变量;fX(x)和hX(x)为2个概率密度函数。从式(1)可以看出,交叉熵可以反应2个概率密度函数之间的差异,当fX(x)=hX(x)时,D(f, h)=0。因此交叉熵也被称为KL距离(Kullback-Leibler distance)。对于式(2)所示的求最大值问题,即
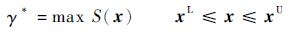
|
(2) |
式中:γ*为优化问题的最优解;S(x)为目标函数;xU和xL分别为设计变量x的上下限。当使用交叉熵方法时,需要先构建一个人造可靠性问题:
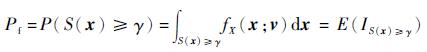
|
(3) |
式中:Pf为可靠性问题的失效概率;γ为一个阈值;v为未知的分布参数;IS(x)≥γ为示性函数。若令ℓ(γ)=Pf,则存在2类估计问题:①给定一个γ求相应的ℓ;②给定一个ℓ求相应的γ。前者是传统的可靠性分析问题,而后者则是一个优化问题。但是在使用交叉熵方法时,并不是事先指定失效事件及相应的阈值,而是通过KL距离去更新概率密度函数fX(x; v),得到一系列的概率密度函数fX(x; v1), fX(x; v2), …, fX(x; v*)。在分布参数v更新的同时,概率密度函数f和变量γ也相应地更新,当v取得最优值v*时,也得到了概率密度函数f的最优值f*=fX(x; v*)和参数γ的最优值γ*。由此可见,最优概率密度函数f*会使得随机变量x有极大概率落在最优解x*上或其附近,则由f*生成的任意随机样本都可以看作是最优解的逼近值,而γ*=S(x*)则为式(2)的最大值。交叉熵方法的核心在于参数v的更新,传统的更新策略如下[12]:
1) 设第k次迭代中,分布参数为vk-1,从fX(x; vk-1)中生成N个随机样本{x1, x2, …, xN},计算目标函数的值{S(xi)}={S(x1), S(x2), …, S(xN)},并将{S(xi)}按照从大到小的次序排列,即S(x1)>S(x2)>…>S(xN)。
2) 计算目标函数的ρ分位数,使得

|
(4) |
式中:bk为功能函数值次序统计量的ρ分位数,即bk=S(xρN),而且目标函数最优值γ*在第k次迭代中的估计值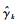
3) 第k+1次迭代中的分布参数vk,可以通过式(5)的最大化问题求得
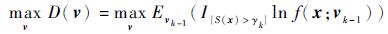
|
(5) |
式(5)对应的随机问题为:对于给定的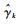
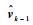
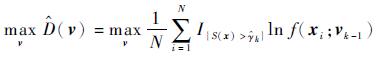
|
(6) |
设从式(6)求得的分布参数为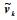
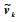
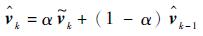
|
(7) |
传统交叉熵方法可以高效地处理大部分的简单优化问题,并且具有极快的收敛速度。但是当目标函数较复杂或约束函数数目较多时,传统方法很可能出现计算精度不足或陷入局部最优的情况,因此,本文针对性地提出3个改进策略,以提高交叉熵优化方法的计算性能。
2 改进的交叉熵方法1) 改进的更新策略
一般地,大部分的优化问题中,交叉熵方法的收敛速度明显高于常用的其他随机优化算法,如遗传算法(Genetic Algorithm, GA)、蚁群优化(Ant Colony Optimization, ACO)算法和粒子群优化(Particle Swarm Optimization,PSO)算法等。交叉熵方法之所以计算速度快,主要是由于更新策略主要是基于ρN个“精英样本”的,其中ρ为稀薄参数,其取值范围通常为0.01~0.1。所以,即使在约束条件较多或者很少有样本点满足约束的情况下,交叉熵方法也可以优先选择最有意义的“精英样本”计算该次迭代中所更新的参数。
同理,由于“精英样本”的数目偏少,并不能完全提取总样本中的有用信息,所以其计算精度是偏低的。另外,由于交叉熵方法的收敛速度过快,所以比较容易陷入局部最优;且如果初期的优化方向错误,则方法可能无法收敛。
本文通过提出“当前精英样本”(current elite samples)和“全局精英样本”(global elite samples)的概念,将参数更新策略改进为
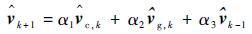
|
(8) |
式中:
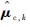
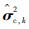

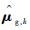

“当前精英样本”为第k次迭代中使得目标函数值最小的前ρN个样本;将第k次的“精英样本”与使得目标函数值最小的历史最优值对比,若“当前精英样本”更好,则将其作为第k次迭代的“全局精英样本”。“全局精英样本”的初值为第一次迭代的“当前精英样本”。
新更新策略的意义在于:迭代历史中的信息并非都是无用的,尽管新的样本点可能更接近最优,但是历次迭代中的历史样本中也可能存在有用信息。因此,充分利用历次迭代中的所有有用样本将有助于提升算法的计算精度。
2) 自适应平滑参数
借鉴只有一个平滑参数的经验,α3的取值通常在0.1~0.3之间,α1的值要大于α2的值。然而该方法在某些条件下依然可能出现计算结果不理想的情况[13],因此有必要增加一种自适应平滑参数。
仔细分析式(8)可以发现,α3的取值越大,则样本保留上一次迭代的趋势越大,在全局搜索的空间更广;相反,α3越小,则新生产样本更趋向于最新的“精英样本”靠拢,即更新的速度更快。因此,为了综合全局搜索能力和迭代后期的收敛速度,理想方案是在搜索的初期α3取较大值,随着迭代的进行,α3逐渐减小并趋近于预设的最小值。对于α1的取值,本文推荐在0.5~0.7之间。据此,本文提出如下平滑参数自适应调整公式:
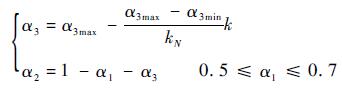
|
(9) |
式中:k为迭代次数; kN为预设的总迭代次数;α3max和α3min分别为α3的最大值和最小值。
3) 变异操作
“变异”是进化计算的基本思想之一,广泛应用于遗传算法、蚁群优化算法和粒子群优化算法等。变异操作的目的在于增加样本的随机性,以降低优化算法陷入局部最优的概率。通常变异操作的方法来对每次迭代过程中更新的参数施加扰动,例如在原有方差的基础上增加一个合适的数。该操作可能使得交叉熵方法的收敛出现明显的波动,但只要扰动量设置合理,就可以在保证计算效率的同时降低算法陷入局部最优的可能性。关于扰动,本文选用了如式(10)所示的扰动函数[14]:
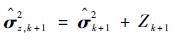
|
(10) |
式中: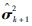
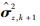
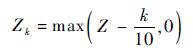
|
(11) |
式中:Z为一个常数,通常建议取5~10。
4) 约束处理方法
对于一个有约束的优化问题,通常不能直接对目标函数值进行处理。本文采用“罚函数”法处理有约束问题,当样本点落入不可行域时,对目标函数值进行惩罚。具体方法为利用一个“惩罚函数”对原始目标函数进行增广,增广后的目标函数为
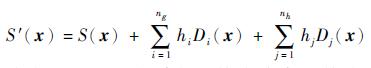
|
(12) |
式中:ng和nh分别为不等式约束和等式约束的数目;hi和hj为罚因子,通常罚因子可以取一个很大的常数以有效区分可行域内外的样本点;Di(x)和Dj(x)为约束函数值乘子,且有:
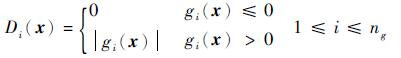
|
(13) |
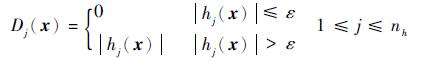
|
(14) |
其中:ε为一个很小的阈值;gi(x)为不等式约束函数;hj(x)为等式约束函数。
综上所述,改进交叉熵(Improved Cross Entropy, ICE)优化方法步骤如下:
步骤1 初始化待定分布参数v0=(μ0, σ0),其中μ0为初始均值, σ0为初始标准差,迭代数记为k=0。
步骤2 从截断正态分布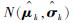
步骤3 根据bk=S′(xρN, k)确定bk的值,并记录前ρN个随机样本{x1, k, x2, k, …, xρN, k}。
步骤4 将{S′(x1, k), S′(x2, k), …, S′(xρN, k)}分别和{S′(x1, k-1), S′(x2, k-1), …, S′(xρN, k-1)}进行比较,若较小,则用xi, k的值替代xi, k-1,i=1, 2, …, ρN,并将这一组值作为全局精英样本。
步骤5 根据式(15)和式(16)分别对步骤3中“当前精英样本”和步骤4中“全局精英样本”的均值和方差,分别记作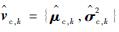
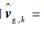
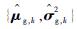
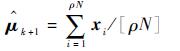
|
(15) |
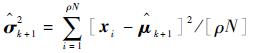
|
(16) |
步骤6 根据式(8)和式(9)进行自适应平滑处理。
步骤7 根据式(10)进行变异操作。
步骤8 若
1) 算例1
该算例来自文献[15]的问题06,求式(17)和式(18)所示的最小化问题:

|
(17) |
式中:13≤x1≤100,0≤x2≤100。文献[15]中给出的最优解参考值为x*=[14.0950, 0.8430]T,最优值参考值为S(x*)=-6961.8139。
在本文的交叉熵优化方法的计算过程中,并不是单纯地以精度或迭代次数为终止条件,而是参考文献[15]中的方法,以迭代计算所需的总样本量为终止条件。因实际计算过程中目标函数和约束条件的复杂程度而异,单层样本量的合理值不尽相同,因而迭代次数也有所差异。本文中均以总样本量5×105为终止条件。
首先尝试采用传统交叉熵优化方法进行计算,单层样本量为2000,迭代次数为250次,稀薄参数ρ=0.01,平滑参数α=0.9,分布参数初值为μ0=[56.5, 50]T和σ0=[20, 20]T。计算结果不甚理想:最优解x*=[14.6044, 2.1558]T,最优值S(x*)=-5582.6584。尽管该最优解满足2个约束条件:g1(x)=-0.3334,g2(x)=-0.6853,但是最优值明显不如文献[15]中的结果。为验证是迭代次数不足还是方法自身缺陷导致的结果不理想,绘制目标函数值变化曲线和最优解变化曲线如图 1所示。
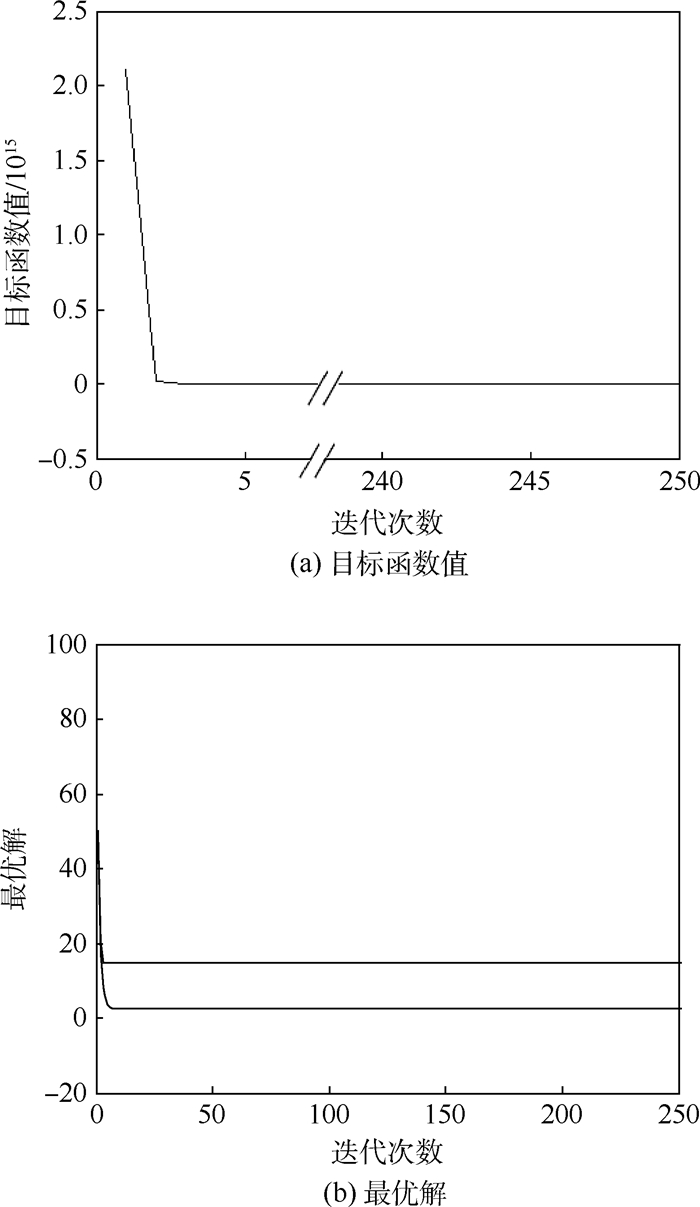
|
| 图 1 算例1目标函数值和最优解迭代曲线(传统交叉熵方法) Fig. 1 Iterative curves of objective function value and optimal solution for Example 1(traditional CE method) |
从图 1中可以看出,传统交叉熵优化方法的收敛速度很快,这一点与可靠性分析中的情况相吻合。目标函数值在大约5次左右已经达到收敛,最优解也在10次迭代后收敛。因此实际上有大约超过200次的迭代过程是没有意义的。为不失一般性,采用完全随机的抽样方法,重复多次试验,并记录优化计算的结果,分析该方法计算不精确是否为个别现象。图 2为重复100次试验的最优值统计结果。

|
| 图 2 算例1统计结果(传统交叉熵方法) Fig. 2 Statistical results of Example 1 (traditional CE method) |
100次的重复试验中,最优值的最小值为min S(x*)=-6036.7026,最大值为max S(x*)=-4646.1624,中位数为median S(x*) =-5331.3439,方差为σ2=1.1241×105。从这一结果可以看出,尽管单次试验中交叉熵优化方法的收敛速度很快,但是其优化结果明显陷入了局部最优,且计算结果不够稳定,因此必须对传统交叉熵方法进行有效的改进。
使用改进的交叉熵方法计算该算例。为了具体分析通过改进更新策略、改进平滑参数、增加变异操作对算法造成的影响,采用依次增加改进策略的方法进行优化计算。第1步,增加变异操作,防止陷入局部最优;第2步,在第1步的基础上引入改进的更新策略和自适应平滑参数,提高计算的精度。
第1步:扰动函数为Zk=max(10-k/10, 0),图 3为增加变异操作后的目标函数值变化曲线图和最优解变化曲线图。
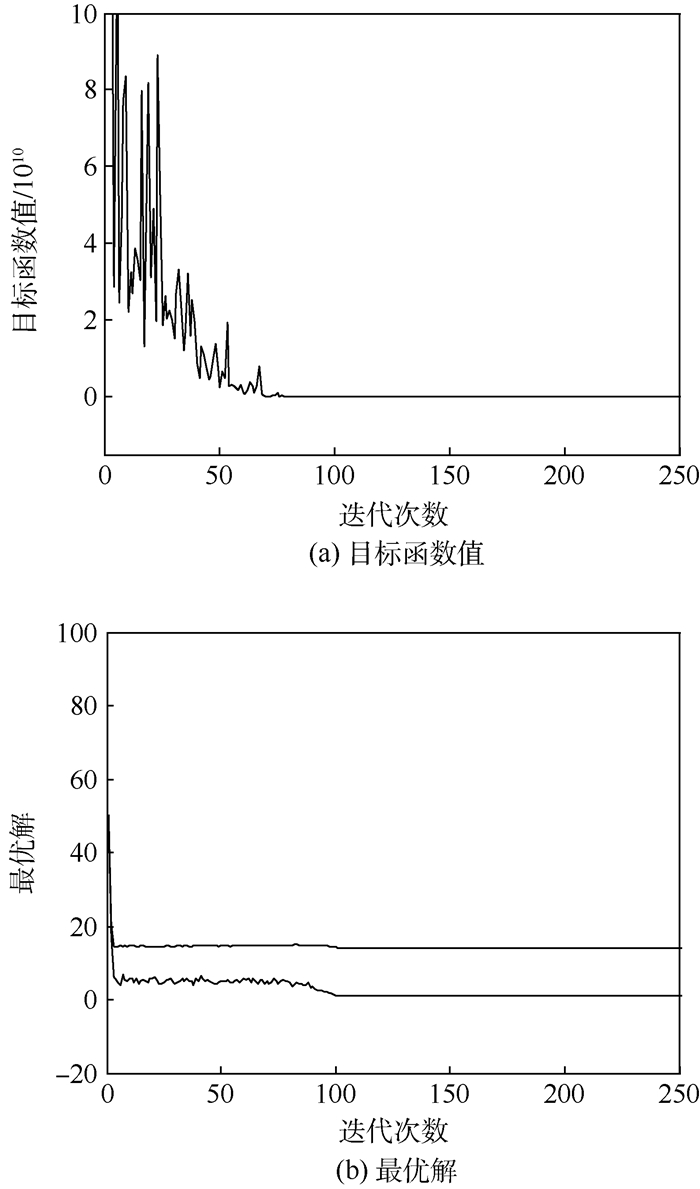
|
| 图 3 算例1目标函数值和最优解迭代曲线(变异操作) Fig. 3 Iterative curves of objective function value and optimum solution for Example 1 (with mutation operation) |
最优解x*=[14.1558, 0.9785]T,最优值S(x*)=-6810.4916。类似的,采用该方法进行100次重复试验,最优值统计结果如图 4所示。
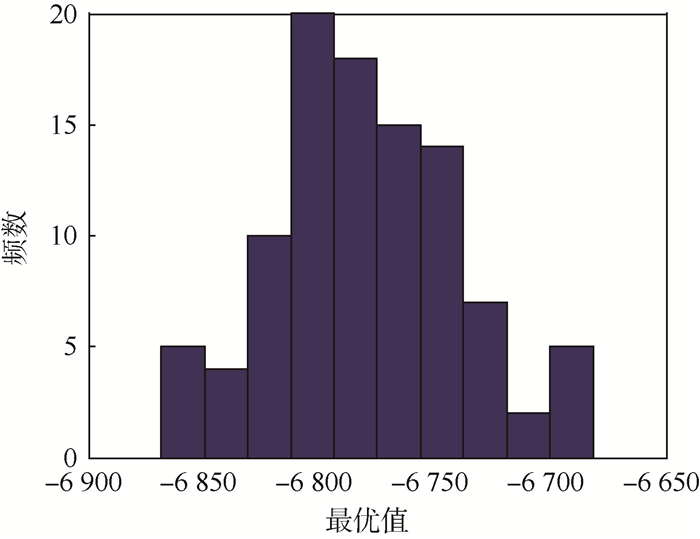
|
| 图 4 算例1统计结果(变异操作) Fig. 4 Statistical results of Example 1 (with mutation operation) |
100次的重复试验中,最优值的最小值为min S(x*)=-6860.4566,最大值为max S(x*)=-6686.3876,中位数为median S(x*)=-6775.7076,方差为σ2=1.8001×103。从这一结果可以看出,增加了变异操作之后,计算结果跳出了局部最优,与理论值已经十分接近;但是从100次的统计结果看,增加了变异操作后,交叉熵方法精度依然不是很高,交叉熵方法的稳健性也有待提高,因此有必要进行第2步改进。
第2步:使用改进的更新策略和自适应的平滑参数,即为完整的改进交叉熵方法。为了和传统交叉熵方对比,设均值和方差的初值点与改进前相同,即:μ0=[56.5, 50]T,标准差初值σ0=[20, 20]T,稀薄参数和单层样本量保持不变,光滑参数与算例1保持一致。使用改进交叉熵方法得到的目标函数值变化曲线图和最优解变化曲线如图 5所示。

|
| 图 5 算例1目标函数值和最优解迭代曲线(改进交叉熵方法) Fig. 5 Iterative curves of objective function value and optimal solution for Example 1(ICE method) |
从图 5可以看出,虽然目标函数值在迭代初期剧烈振荡,但是在75次迭代后趋于收敛,最优解则在100迭代左右趋于收敛。优化计算的结果为:最优解x*=[14.0892, 0.8309]T,最优值S(x*)=-6 968.5867,约束函数g1(x)=0.0055,g2(x)=0.0061。虽然该最优解略微没有满足约束条件,但是无论是最优解还是最优值的计算结果,均与理论值十分接近,因此可以认为,相较传统交叉熵方法,改进交叉熵方法不仅可以有效防止算法陷入局部最优,还可以明显提高计算精度。另外,在实际计算的过程中,如果想要加快收敛的速度,只需将式(11)中的参数Z适当调小即可,但是注意Z取值过小可能造成变异不足。最后,采用改进交叉熵方法进行100次重复试验,结果如图 6所示。

|
| 图 6 算例1统计结果(改进交叉熵方法) Fig. 6 Statistical results of Example 1 (ICE method) |
从图 6可以看出改进后的交叉熵方法鲁棒性明显提高,绝大部分的最优值计算结果都十分接近理论值。
为了进一步显示改进方法的优越性,尝试从重要抽样密度均值的初值μ0入手,将μ0设置在x的约束范围之外,以检测该方法的通用性。表 1为μ0取不同值时改进前后的优化计算结果,SCE(x*)和SICE(x*)分别为采用传统交叉熵方法和改进交叉熵方法求得的目标函数值。
| μ0 | SCE(x*) | SICE(x*) |
| [56.5, 50]T | -5 582.658 4 | -6968.5867 |
| [100, 100]T | 1.9466×1014 | -6968.5868 |
| [0, 0]T | -6289.1210 | -6968.5866 |
| [150, 150]T | 1.1289×1016 | -6968.5867 |
| [-150, 150]T | 1.1618×1014 | -6968.5868 |
从表 1可以看出,当均值的初值点处于感兴趣的区域外时,传统交叉熵方法出现了明显的错误,这种错误并不是由迭代次数不足引起的,而是寻优方向出现了错误导致算法没有收敛;相反,改进交叉熵方法不论初值点是否在感兴趣的区域,最终都能够得到十分精确的结果,证明改进交叉熵方法鲁棒性更强。
2) 算例2
该算例来自文献[15]的问题16,由于该问题过于冗长,对于该问题的描述详见文献[15]。该问题一共有5个输入变量,38个不等式约束,是一个约束情况较为复杂的优化算例。文献[15]中给出的最优值参考值为S(x*)=-1.90515526,最优解为x*=[705.175, 68.600, 102.900, 282.325, 37.584]T。
分别采用改进前后的交叉熵方法进行100次重复试验。为了方便对比,同时防止改进前的传统交叉熵方法出现找不到最优解的情况发生,将重要抽样密度均值设在感兴趣的区域之内,即μ0=[80, 150, 60, 250, 55]T。标准差初值σ0=[30, 30, 30, 30, 30]T,单层样本量N=2500,迭代次数为200次,稀薄参数ρ=0.01。传统交叉熵方法光滑参数α=0.8,改进交叉熵方法参数设定与算例1相同。
取其中一次的试验结果绘制目标函数值和最优解迭代曲线如图 7所示。
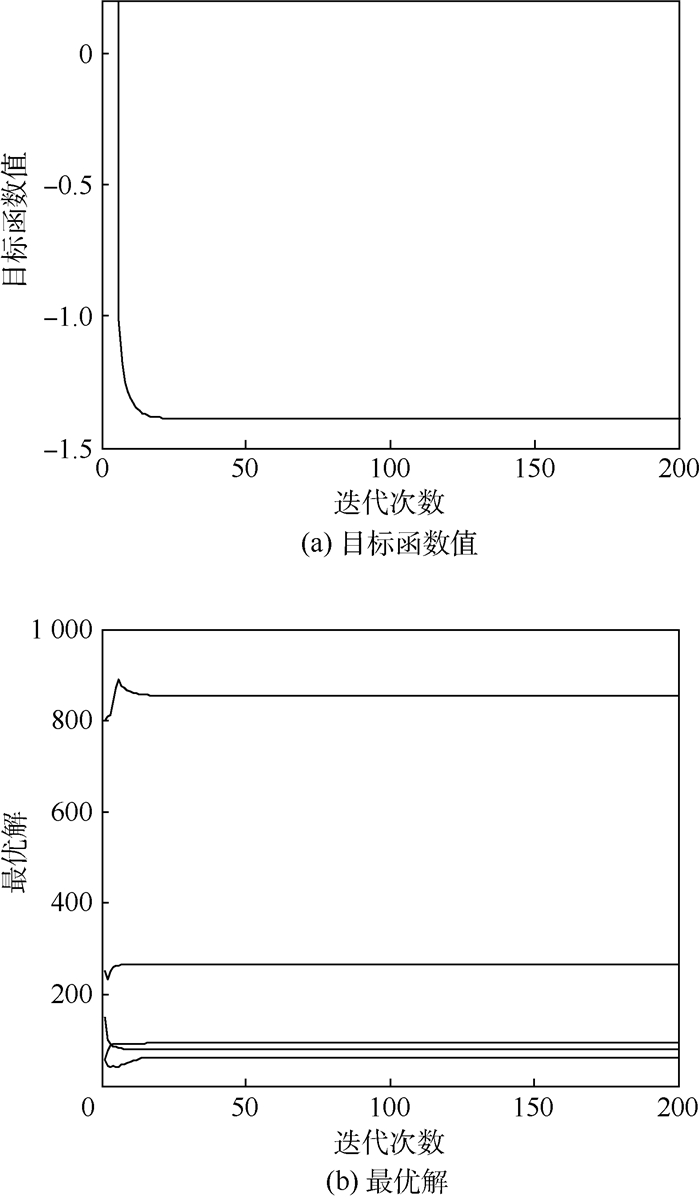
|
| 图 7 算例2目标函数值和最优解迭代曲线(传统交叉熵方法) Fig. 7 Iterative curves of objective function value and optimal solution for Example 2(traditional CE method) |
采用传统交叉熵方法,结果依然不是非常理想,目标函数最优值S(x*)=-1.387 7,最优解为x*=[854.724, 78.267, 93.233, 266.129, 63.013]T。
改进交叉熵方法,结果与理论值十分接近,目标函数最优值S(x*)=-1.9052,最优解为x*=[705.175, 68.600, 102.900, 282.325, 37.584]T。值得注意的是,本算例中目标函数的变化曲线并不像算例1中波动明显,这是由于本算例中目标函数值的波动幅度过大,因此这里舍去了部分目标函数值极大的点,仅画出波动较明显的区域。其中一次结果的目标函数值和最优解迭代曲线如图 8所示。表 2给出了改进前后的交叉熵方法目标函数值收敛情况。
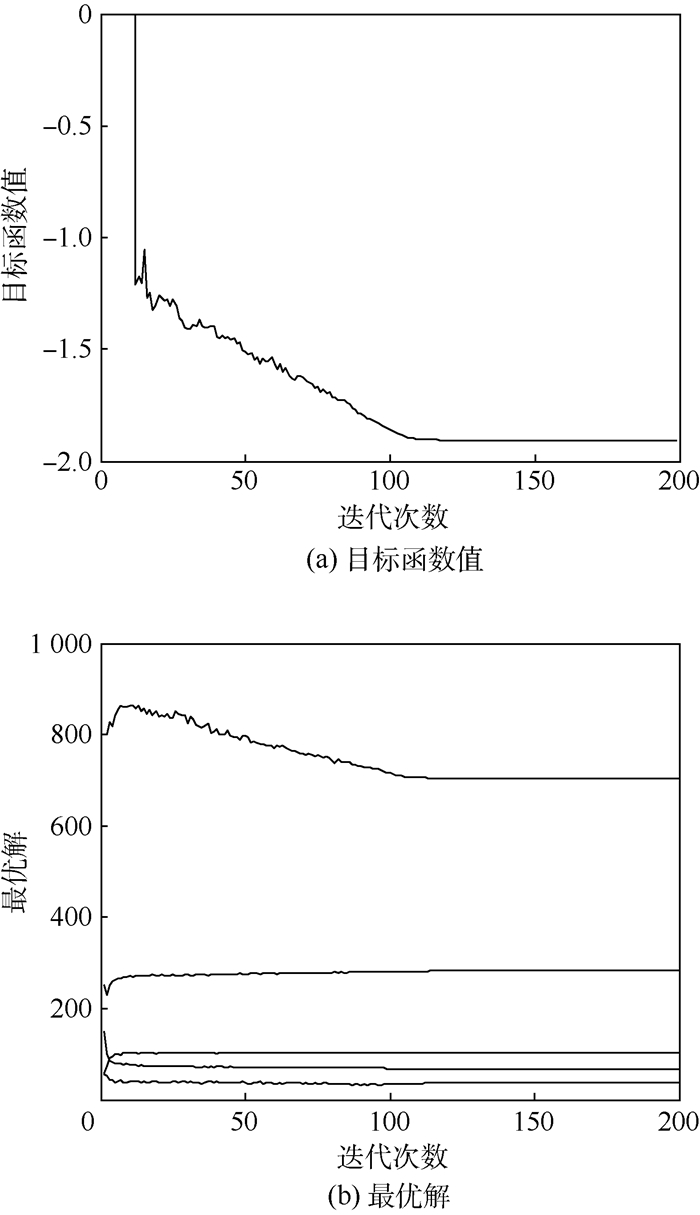
|
| 图 8 算例2目标函数值和最优解迭代曲线(改进交叉熵方法) Fig. 8 Iterative curves of objective function value and optimal solution for Example 2 (ICE method) |
| 迭代次数 | SCE(x*) | SICE(x*) |
| 1 | 3.046 0×1017 | 1.870 5×1017 |
| 2 | 1.885 2×1016 | 2.409 6×1016 |
| 3 | 4.116 8×1015 | 5.599 3×1015 |
| 4 | 8.374 1×1014 | 3.043 2×1015 |
| 5 | 1.273 0×1014 | 9.092 1×1014 |
| 6 | -1.002 9 | 3.657 2×1014 |
| 9 | -1.141 5 | 1.002 9×1013 |
| 10 | -1.312 0 | -0.893 3 |
| 50 | -1.387 7 | -1.508 1 |
| 100 | -1.387 7 | -1.854 4 |
| 150 | -1.387 7 | -1.905 2 |
| 200 | -1.387 7 | -1.905 2 |
从表 2可以看出,传统交叉熵方法在第10次左右便已经接近收敛,并且陷入了局部最优;而改进交叉熵方法虽然收敛速度稍慢,但是却可以逐渐找到全局最优解。
由于一次试验的结果具有一定的随机性,因此绘制100次重复试验的结果统计对比如图 9所示。
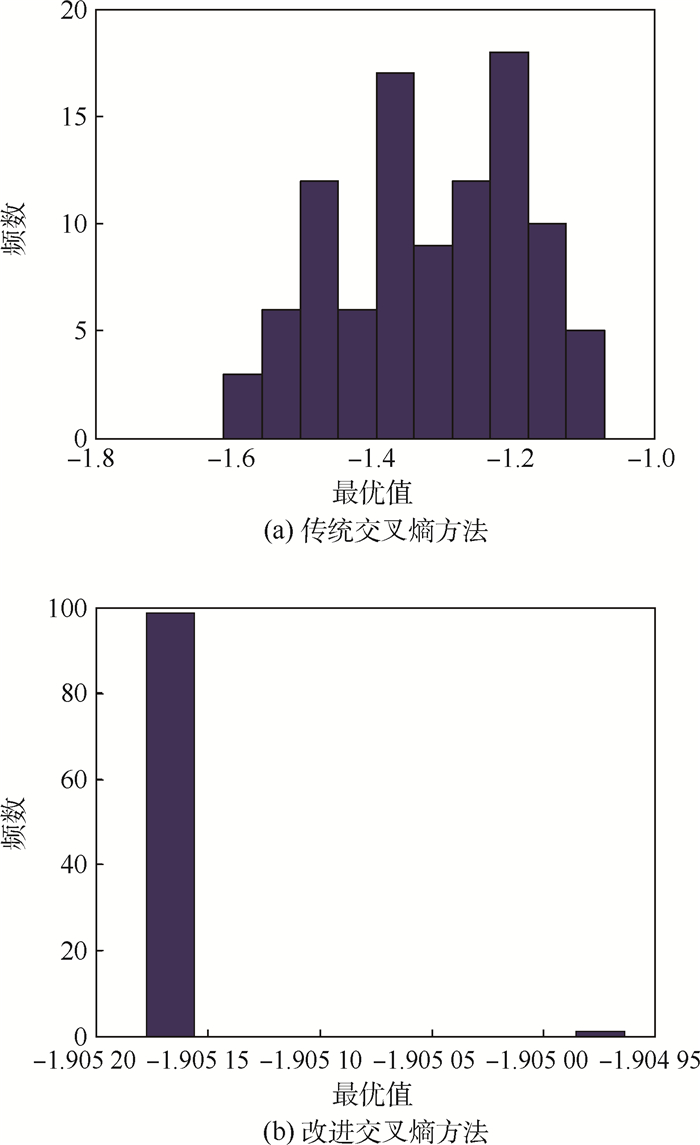
|
| 图 9 算例2统计结果 Fig. 9 Statistical results of Example 2 |
100次的重复试验中,传统交叉熵方法目标函数最小值为min SCE(x*)=-1.6175,最大值为max SCE(x*)=-1.080 6,中位数为median SCE (x*)=-1.3255,方差为σCE2=0.0234。改进交叉熵方法目标函数最小值为min SICE(x*)= -1.90520,最大值为max SICE(x*)=-1.90497,中位数为median SICE(x*)=-1.90516,方差为σICE2= 1.8415×10-9。对比改进前后的统计结果,可以明显看出改进交叉熵方法有更大的概率求得接近理论值的解。不仅如此,改进交叉熵方法比改进前的结果拥有更好的鲁棒性,因此可以认为在处理含有多个不等式约束的优化问题时,改进的交叉熵方法在计算的精确性,鲁棒性方面都具有明显的优势。
3) 算例3
该算例来自文献[16],是一个传动箱优化设计问题。该问题的目标函数和约束函数为

|
(18) |
式中:xi≥0, i=1, 2, …, 6。文献[16]中给出的目标函数参考值为S(x*)=135.0760,使用传统交叉熵方法和改进交叉熵方法计算出的目标函数值分别为:SCE(x*)=136.8762和SICE(x*)=135.2799,可以看出改进交叉熵方法结果更接近参考值。为了进一步衡量改进前后方法的鲁棒性,做100次重复试验,其结果统计对比如图 10所示。
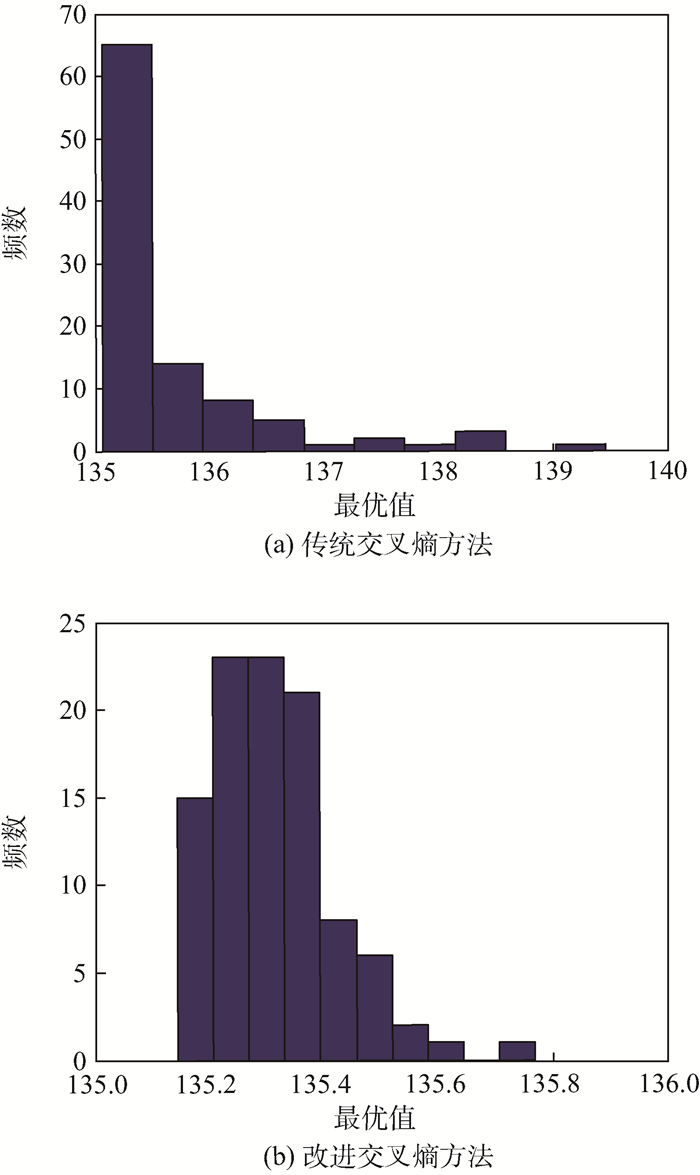
|
| 图 10 算例3统计结果 Fig. 10 Statistical results of Example 3 |
从图 10可以看出,传统交叉熵方法得到的目标函数值最大值超过了139,而改进交叉熵方法最大值不超过136,因此可以认为改进交叉熵方法具有更好的鲁棒性。同时注意到即使是改进交叉熵方法,其计算结果和理论值仍存在少许误差,因此将来仍有改进的空间。
4 结论本文针对传统交叉熵方法的缺陷,提出了一种高效、高鲁棒性的改进交叉熵方法,可以得出以下结论:
1) 提出一种增加“全局精英样本”的方法,适当降低传统交叉熵方法的计算速度,保留迭代历史中的有用信息并应用于参数的更新中,可提出计算的精确度。
2) 引入变异操作,使得改进交叉熵方法在其迭代初期尽可能在更大的范围类搜索可行解,在迭代后期逐渐趋于最优解。
3) 改进交叉熵方法,保留了传统交叉熵方法一定的高效性,提高了精确性,降低了陷入局部最优的可能性。
4) 通过多次的重复试验,证明改进交叉熵方法鲁棒性更高,尤其是对重要抽样密度函数均值的初值点不敏感,因此可以在不同的初值条件、不同的随机种子的前提下都尽可能趋于一个最优解。
| [1] | HAFTKA R T, GVRDAL Z. Elements of structural optimization[M]. Dordrecht: Kluwer Academic Publishers, 1990. |
| [2] | RUBINSTEIN R Y. Optimization of computer simulation models with rare events[J]. European Journal of Operational Research, 1997, 99 (1): 89–112. DOI:10.1016/S0377-2217(96)00385-2 |
| [3] | RUBINSTEIN R Y. The cross-entropy method for combinatorial and continuous optimization[J]. Methodology & Computing in Applied Probability, 1999, 1 (2): 127–190. |
| [4] | HELVIK B E, WITTNER O. Using the cross-entropy method to guide/govern mobile agent's path finding in networks[M]. Berlin: Springer, 2001. |
| [5] | ALON G, KROESE D P, RAVIV T, et al. Application of the cross-entropy method to the buffer allocation problem in a simulation-based environment[J]. Annals of Operations Research, 2005, 134 (1): 137–151. DOI:10.1007/s10479-005-5728-8 |
| [6] | KUO C, YEARGAIN J R, DOWNEY W J, et al. Solving the vehicle routing problem with stochastic demands using the cross-entropy method[J]. Annals of Operations Research, 2005, 134 (1): 153–181. DOI:10.1007/s10479-005-5729-7 |
| [7] | KROESE D P, POROTSKY S, RUBINSTEIN R Y. The cross-entropy method for continuous multi-extremal optimization[J]. Methodology & Computing in Applied Probability, 2006, 8 (3): 383–407. |
| [8] | HO S L, YANG S. The cross-entropy method and its application to inverse problems[J]. IEEE Transactions on Magnetics, 2010, 46 (8): 3401–3404. DOI:10.1109/TMAG.2010.2044380 |
| [9] |
丁卫平, 王建东, 陈森博, 等. 基于改进混合蛙跳算法的粗糙属性交叉熵优化约简[J].
南京大学学报(自然科学), 2014, 50 (2): 159–166.
DING W P, WANG J D, CHEN S B, et al. Rough attribute reduction with cross-entropy based on improved shuffled frog-leaping algorithm[J]. Journal of Nanjing University(Natural Sciences), 2014, 50 (2): 159–166. (in Chinese) |
| [10] |
李国成, 肖庆宪. 求解高维函数优化问题的交叉熵蝙蝠算法[J].
计算机工程, 2014, 40 (10): 168–174.
LI G C, XIAO Q X. Cross-entropy bat algorithm for solving high-dimensional function optimization problem[J]. Computer Engineering, 2014, 40 (10): 168–174. DOI:10.3969/j.issn.1000-3428.2014.10.032 (in Chinese) |
| [11] | GHIDEY H.Reliability-based design optimization with cross-entropy method[D].Trondheim:Norwegian University of Science and Technology, 2015. |
| [12] |
李洪双, 马远卓.
结构可靠性分析与随机优化设计的统一方法[M]. 北京: 国防工业出版社, 2015: 146-147.
LI H S, MA Y Z. Unified methods for structural reliability analysis and stochastic optimization design[M]. Beijing: National Defense Industry Press, 2015: 146-147. (in Chinese) |
| [13] | HUI K P, BEAN N, KRAETZL M, et al. The tree cut and merge algorithm for estimation of network reliability[J]. Probability in the Engineering & Informational Sciences, 2002, 17 (1): 23–45. |
| [14] |
吴烈. 电磁场逆问题鲁棒优化设计理论和算法研究[D]. 杭州: 浙江大学, 2012.
WU L.Numerical methodologies for robust optimizations of inverse problems[D].Hangzhou:Zhejiang University, 2012(in Chinese). |
| [15] | LIANG J J, RUNARSSON T P, MEZURA-MONTES E, et al.Problem definitions and evaluation criteria for the CEC 2006 special session on constrained real-parameter optimization[R].Singapore:Nanyang Technological University, 2006. |
| [16] |
彭宏, 杨立洪, 郑咸义, 等. 计算工程优化问题的进化策略[J].
华南理工大学学报(自然科学版), 1997, 25 (12): 17–21.
PENG H, YANG L H, ZHENG X Y, et al. A new evolutionary strategy for solving engineering optimization problems[J]. Journal of South China University of Technology(Natural Science Edition), 1997, 25 (12): 17–21. DOI:10.3321/j.issn:1000-565X.1997.12.004 (in Chinese) |



