随着航天事业的发展,在轨航天器日益增多。若仍采用依赖地面测控支持的导航模式,不仅会提高航天器的运营成本,而且无法确保航天器在特定情况下的生存能力。因此,自主导航是未来航天器发展的核心技术和关键技术[1]。目前,借助全球卫星导航系统(Global Navigation Satellite System,GNSS)低轨航天器已基本实现了自主导航,可完成如自主交会对接、短期自主运行等任务。局限于导航卫星的轨道高度和电磁信号的辐射角约束,GNSS难以应用于高轨航天器和深空探测器的自主导航任务[2]。研究适用于上述2种航天器的自主导航技术,是业界研究的热点。
X射线脉冲星导航是一种新兴的航天器自主导航方法,优势有:能提供高精度的参考时间基准,导航精度高,对导航探测器精度要求较低。同卫星导航相比,X射线脉冲星导航还具有可同时服务于近地航天器和深空探测器的优势[3]。由于其具有广阔的应用前景,X射线脉冲星导航技术得到了国内外的广泛关注[4-7]。经过近30年的发展,该导航技术已经逐步从概念研究阶段进入关键技术攻坚阶段。
脉冲星数据库的构建是X射线脉冲星导航的一项关键技术。构建脉冲星数据库涵盖了脉冲星的空间分布、周期分布和信号等参数的测定工作[8]。其中,脉冲星信号的脉冲模板是脉冲星信号处理的基本输入量,也是脉冲星数据库构建中的一项重要内容。将在轨恢复的轮廓与脉冲模板对比,可以估计出脉冲到达航天器的到达时间(Time of Arrival,TOA)[9]。TOA是X射线脉冲星导航的基本测量量。若脉冲模板存在偏差,则会导致TOA的估计结果出现偏差,从而降低了导航系统的性能。为此,分析影响脉冲模板的因素,并提出相应的削弱策略,可为提升脉冲星导航的性能提供有力支持。
本文首先简要介绍了脉冲星脉冲模板构建的基本原理。然后着重分析了脉冲星角位置误差对模板构建的影响,推导得到此系统误差的年化平均值以及任意弧段积分的解析表达式。最后提出一种系统误差削弱策略。
1 脉冲星脉冲模板构建的基本原理在实际的空间X射线脉冲星观测中,脉冲星信号的观测量就是脉冲星辐射的X射线光子[10]。由于存在脉冲星自转频率变化、航天器轨道信息不准确等因素,难以在轨恢复出高精度的脉冲星脉冲模板。为此,将探测到的光子TOA序列转换到太阳系质心(Solar System Barycentre, SSB)以消除航天器运动、相对论效应等影响外,还需搜索信号周期,并将每个时段获得的轮廓进行相位对齐[11]。
1.1 光子到达时间转换考虑到周年视差、Roemer延迟、色散延缓和引力时延等效应,令光子到达探测器的时间为tSC,光子到达真空SSB的时间为tSSB,相应的时间转换模型可写为
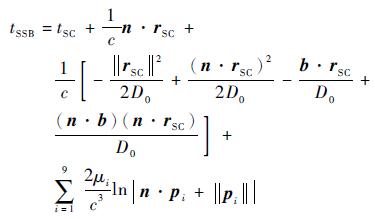
|
(1) |
式中:等号右边第2项为一阶多普勒延迟,第3项为由周年视差效应引起的,第4项为Shapiro延迟效应;n为脉冲星位置矢量;rSC为航天器相对于SSB的位置矢量;c为光速;D0为脉冲星在基准传播时间T0时的位置;b为SSB相对于太阳质心的位置矢量;pi为航天器相对于第i颗行星的位置矢量;μi为第i颗行星的引力常数。若观测脉冲星的赤经和赤纬分别为α和δ,则其矢量方向为
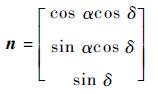
|
(2) |
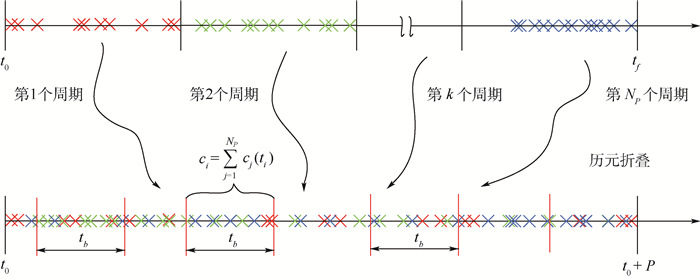
假设在观测时间t内,探测器可接收到一段光子TOA序列。按照试验周期P进行历元折叠,即将该光子TOA序列分为NP段。然后,将NP段长度为试验周期P的光子TOA序列分为Nb份,即将一个周期的相位分为Nb份。各个试验周期的光子TOA依次累积按相位到第1段上,得到第i个相位的光子数为ci(见图 1)[12]。建立χ2为
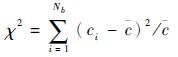
|
(3) |
|
| 图 1 历元折叠过程 Fig. 1 Epoch folding process |
式中:c为平均光子数。
一直变化试验周期P,使χ2达到最大值。χ2最大值对应的P即为脉冲星的自转周期。
1.3 相位对齐通过1.2节周期寻找过程,可以获得最佳的折合周期Pbest。由于每段观测时间的脉冲星信号初相不同,需要把不同观测时段的初相对齐。因此,可通过交叉互相关、傅里叶变换法等将后续观测时段得到的轮廓与第1个观测时段得到的轮廓作比较,求得初相差。根据不同的初相差,就可将后续时段得到的恢复轮廓折合到第1个时段,从而获得高信噪比的信号轮廓。
2 脉冲星角位置误差的影响目前通常采用甚长基线干涉测量(Very Long Baseline Interferometer,VLBI)来测定脉冲星的角位置。基于当前的VLBI测量水平,脉冲星角位置的精度可以达到1mas(毫角秒)附近[13]。
2.1 脉冲星角位置误差引起的系统误差设脉冲星角位置的测量误差为(Δα, Δδ),则脉冲星指向误差为

|
(4) |
则有脉冲星指向为
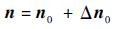
|
(5) |
式中:n0为脉冲星的实际方向矢量。
从式(1)可知,脉冲星的角位置误差通过影响脉冲星的方向矢量来影响时间转换精度,从而影响脉冲模板构建的精度。因此,式(1)对脉冲星方向矢量的导数可用来衡量脉冲星角位置误差的影响。将pi=rSC-bi代入式(1),得到其具体的误差传播函数为
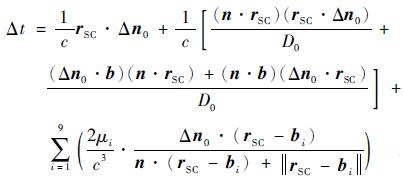
|
(6) |
式中:bi为第i颗行星相对SSB的位置矢量。航天器到SSB的矢量rSC可表示为
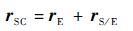
|
(7) |
式中:rE为地球到SSB的位置矢量; rS/E为航天器到地球的位置矢量。对于高轨航天器,||rS/E||«||rE||总成立,分析系统误差影响时可略去rS/E的影响,即
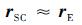
|
(8) |
则式(6)可写为

|
(9) |
记式(9)等式右侧的3项分别为Δt1、Δt2、Δt3,以Crab脉冲星为例,基于DE405进行仿真,取其角位置误差为1mas,分别绘制脉冲星角位置误差引起的总的系统误差与Δt1、Δt2、Δt3随时间变化曲线,结果如图 2所示。

|
| 图 2 脉冲星角位置误差引起的系统误差 Fig. 2 Systom error caused by pulsar angular position error |
目前对于简化的时间转换模型而言,其精度约是1μs,从图 2可以看出,1mas的脉冲星角位置误差的影响在全年呈周期变化,且在全年大部分时间的影响大于1μs,这一误差的影响极为可观。另外,脉冲星角位置误差所引起时延主要是Δt1所造成的。故分析脉冲星角位置误差对脉冲模板构建的影响时,其误差传播方程可简化为

|
(10) |
不考虑摄动影响以及地球轨道根数的不确定性,则地球相对SSB的位置矢量rE可表示为

|
(11) |
式中:M为地球轨道坐标系到太阳系质心惯性系的坐标转换矩阵;M1和M3分别为绕X轴和Z轴旋转的方向余弦阵; a, e, i, Ω, ω为地球绕SSB运动轨道的轨道根数;E为偏近点角;rE/O为地球在轨道坐标系中表示的位置矢量,即

|
(12) |
令
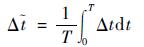
|
(13) |
为系统误差的年化平均值。T=365.242 2d为地球公转周期。在较大时间尺度上认为脉冲星光子到达为均匀分布。将式(10)代入式(13)得到
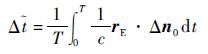
|
(14) |
式中:Δn0为与时间无关的常矢量。将式(11)与式(12)代入式(14),考虑到

|
(15) |
式中:r=||rE||; 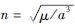
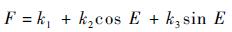
|
(16) |
的形式,则有
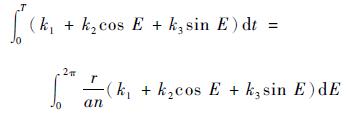
|
(17) |
将r=a(1-ecos E)代入式(17),则可转化为求解以下3个积分:
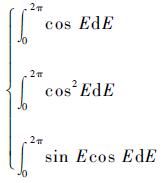
|
(18) |
由于

|
(19) |
因此可以得出:①按年累积数据,系统误差的影响会大幅度下降。②角位置误差引起的系统误差中的周期项虽会被消除,但会留下一个长期项。
下面通过公式推导得到其周年特性的解析表达式,以便于仿真验证。
将r=a(1-ecos E)代入式(15)得到

|
(20) |
将式(11)、式(12)及式(20)代入式(14),进行推导,可得
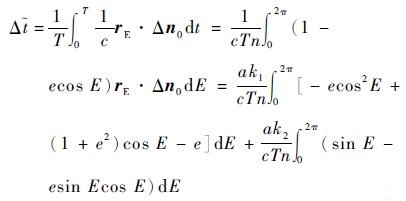
|
(21) |
式中:
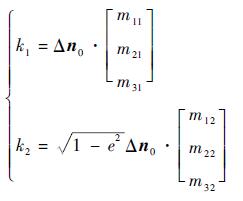
|
(22) |
又
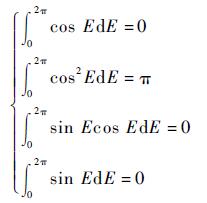
|
(23) |
则有
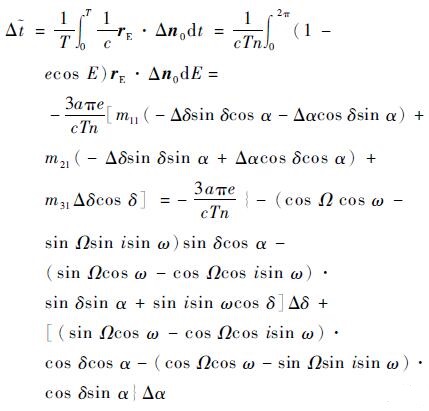
|
(24) |
根据式(24)可知,若地球轨道根数和脉冲星的角位置误差确定,则角位置误差所引起系统误差Δt的年化平均值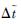
| 轨道根数 | 数值 |
| 半长轴/AU | 0.9999858 |
| 偏心率 | 0.01667835 |
| 轨道倾角/(°) | 23.44 |
| 升交点黄经/(°) | 0 |
| 近日点黄经/(°) | 103.30275 |
取1mas的脉冲星角位置误差,对文献[15]中提及的10个脉冲星,分别计算其Δt的最大值与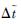
| 脉冲星 | Max(Δt)/μs | Δ/(10-8s) |
| J0534+2200 | 2.3388 | -2.0555 |
| J1513-5908 | 1.7748 | 3.8512 |
| J1846-0258 | 2.6979 | -1.7737 |
| J0540-6919 | 2.5157 | -6.4059 |
| J0835-4510 | 2.5553 | -3.6324 |
| J1824-2452 | 2.2959 | 0.9289 |
| J1959-2048 | 2.6756 | -1.6696 |
| J0437-4715 | 2.8082 | -7.1214 |
| J0218+4232 | 2.6231 | -4.2932 |
| J1939+2134 | 2.9625 | -5.1393 |
由表 2可以看出,对此项系统误差取年化平均值均可将其大幅度削弱,但仍存在长期项。从而验证了由式(13)~式(19)的理论分析所得到的2个结论。
3 系统误差的削弱策略由2.2.2节分析可知,脉冲星角位置误差的影响函数是一个以一年为周期的类似正弦函数。因此,为了削弱脉冲星角位置误差对脉冲模板构建的影响,在进行历元累积时,应尽量选择相对正弦曲线零点对称的时间段。
实际上,考虑到太阳规避等因素,无法对X射线脉冲星进行全年观测。为此,需考虑任意弧段下测量误差影响的特性。取弧段(E1, E2),对应时间段为(t1, t2),根据式(21)~式(24)可得
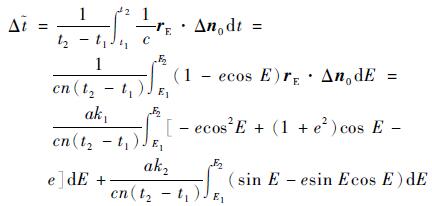
|
(25) |
由于
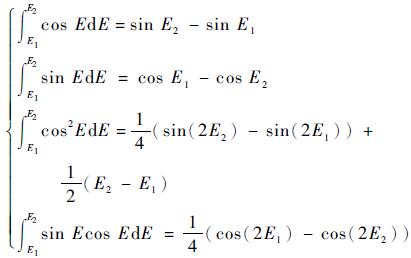
|
(26) |
将式(26)代入式(25)可得
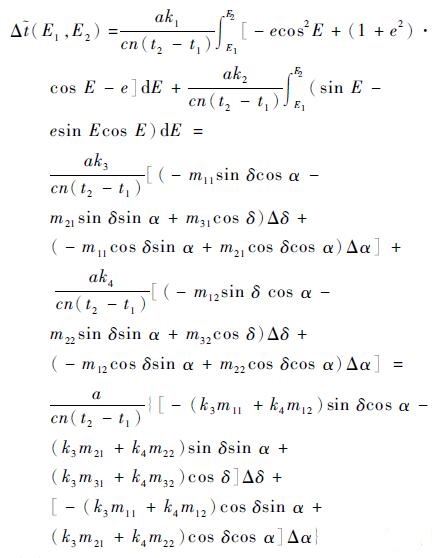
|
(27) |
式中:
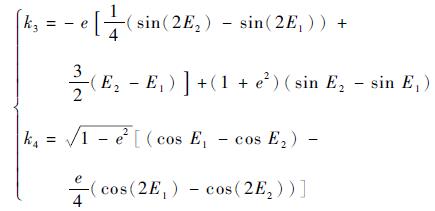
|
(28) |
基于蒙特卡罗打靶,生成每组观测时长为1h的1000组光子TOA序列,在1年中每2d进行1h的仿真模拟,图 3给出了1mas脉冲星角位置误差导致的系统误差在一年内的变化情况以及通过历元累积对此系统误差的削弱情况。
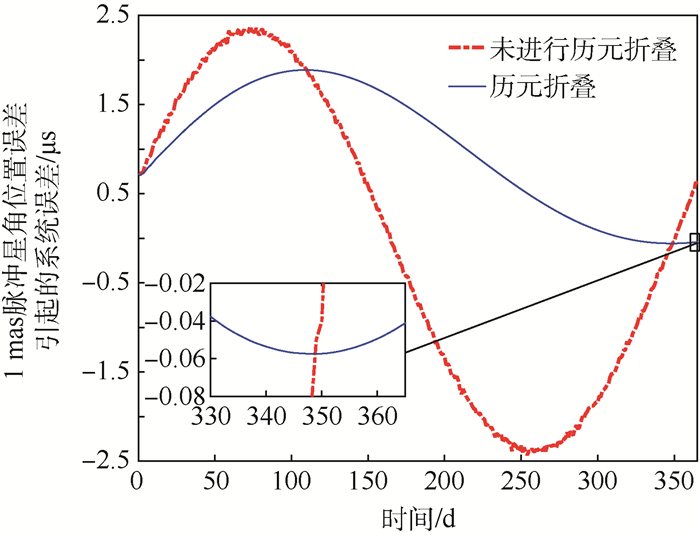
|
| 图 3 历元累积对脉冲星角位置误差的削弱情况 Fig. 3 Pulsar angular position error reduced by epoch accumulation |
由图 3可知,对于非对称时间段的系统误差进行历元累积,此误差不断增大,之后随着对称时间段数据的加入,可使其大幅度削弱。通过一年的观测,可将1mas脉冲星角位置误差的影响从1~2μs降低到0.1μs附近。因此,若按周期性系统误差的周期对称选取时间段进行历元累积,可削弱该系统误差的影响。
在实际观测中,脉冲星并非全年可见,比如Crab脉冲星在6月份不可见。以Crab脉冲星为例,表 3显示了考虑其不可见时段时选取对称时段与非对称时段进行历元累积的结果。由表 3可以看出,当选取对称时段进行历元累积构建脉冲模板时,其系统误差明显低于选取非对称时段的情况。
| 时段 | 所选具体时间段/d | 脉冲最终系统误差/μs |
| 对称时段 | 1~90, 241~330 | -0.0398 |
| 非对称时段 | 1~120, 241~330 | 0.6100 |
综上所述,在构建脉冲模板时,根据角位置误差所造成的系统误差的周期选取对称时段进行历元累积可以有效削弱此项系统误差,进而提高脉冲模板的精度。
4 结论1) 构建脉冲模板时,取1mas的脉冲星角位置误差,其造成的系统误差在1年内的大部分时间大于1μs,不可忽略。
2) 经过公式推导,得到此系统误差的年化平均值的解析表达式,计算结果表明,对脉冲星角位置误差引起的系统误差取年化平均值可使其大幅度削弱,但仍存在长期项。
3) 以Crab脉冲量为例,按周期性系统误差的周期对称选取时间段进行历元累积,可将1mas脉冲星角位置误差的影响从1~2μs降低到0.1μs附近。
4) 在构建脉冲模板时,根据角位置误差所造成的系统误差的周期选取对称时段进行历元累积可以有效削弱此项系统误差,进而提高脉冲模板的精度。
5) 本研究可以为优化X射线脉冲星的观测任务以及X射线脉冲模板构建提供理论支持。
| [1] |
郑伟, 王奕迪, 汤国建, 等.
X射线脉冲星导航理论与应用[M]. 北京: 科学出版社, 2015: 1-20.
ZHENG W, WANG Y D, TANG G J, et al. X-ray pulsar-based navigation:Theory and applications[M]. Beijing: Science Press, 2015: 1-20. (in Chinese) |
| [2] |
何清举, 孙前贵. 利用GNSS实现高轨卫星自主导航的新方案[J].
飞行器测控学报, 2010, 29 (1): 7–11.
HE Q J, SUN Q G. A new solution of autonomous navigation for GEO satellites based on GNSS[J]. Journal of Spacecraft TT&C Technology, 2010, 29 (1): 7–11. (in Chinese) |
| [3] |
帅平, 李明, 陈绍龙, 等.
X射线脉冲星导航系统原理与方法[M]. 北京: 中国宇航出版社, 2009.
SHUAI P, LI M, CHEN S L, et al. X-ray pulsar-based navigation system:Theory and methods[M]. Beijing: China Astronautic Publishing House, 2009. (in Chinese) |
| [4] | SHEIKH S I.The use of variable celestial X-ray sources for spacecraft navigation[D].Washington, D.C.:University of Maryland, 2005. |
| [5] | WOODFORK D W.Use of X-ray pulsar for aiding GPS satellite orbit determination[D].Alabama:Air University, 2005. |
| [6] |
邓新坪. X射线脉冲星自主导航研究[D]. 北京: 中国科学院大学, 2013.
DENG X P.Research on autonomous navigation using X-ray pulsars[D].Beijing:University of Chinese Academy of Sciences, 2013(in Chinese). |
| [7] | WANG Y D, ZHENG W, SUN S M, et al. X-ray pulsar-based navigation system with the errors in the planetary ephemerides for earth-orbiting satellite[J]. Advances in Space Research, 2013, 51 (12): 2394–2404. DOI:10.1016/j.asr.2013.02.007 |
| [8] |
周庆勇, 刘思伟, 郝晓龙, 等. 空间X射线观测确定脉冲星星历表参数精度分析[J].
物理学报, 2016, 65 (7): 368–377.
ZHOU Q Y, LIU S W, HAO X L, et al. Analysis of measurement accuracy of ephemeris parameters for pulsar navigation based on the X-ray space observation[J]. Acta Physica Sinica, 2016, 65 (7): 368–377. (in Chinese) |
| [9] | EMADZADEH A A, SPEYER J L, HADAEHG F Y.A parametric study of relative navigation using pulsars[C]//Proceeding of the 63rd Annual Meeting of the Institute Navigation, 2007:454-459. |
| [10] | LIU J, MA J, TIAN J, et al. X-ray pulsar navigation method for spacecraft with pulsar direction error[J]. Advances in Space Research, 2010, 46 (11): 1409–1417. DOI:10.1016/j.asr.2010.08.019 |
| [11] |
葛明玉. 脉冲星的X射线辐射特性研究[D]. 北京: 中国科学院研究生院, 2012.
GE M Y.The X-ray emission of pulsars[D].Beijing:Graduate University of Chinese Academy of Sciences, 2012(in Chinese). |
| [12] | EMADZADEH A A, SPEYER J L. Navigation in space by X-ray pulsars[M]. Berlin: Springer, 2010: 13-33. |
| [13] |
王奕迪. X射线脉冲星信号处理与导航方法研究[D]. 长沙: 国防科学技术大学, 2016.
WANG Y D.X-ray pulsar-based navigation:Signal processing and positioning algorithms[D].Changsha:National University of Defense Technology, 2016(in Chinese). |
| [14] |
张洪波.
航天器轨道力学理论与方法[M]. 北京: 国防工业出版社, 2015.
ZHANG H B. Theories and methods of spacecraft orbital mechanics[M]. Beijing: National Defend Industry Press, 2015. (in Chinese) |
| [15] |
费保俊.
相对论在现代导航中的应用[M]. 北京: 国防工业出版社, 2015: 176-177.
FEI B J. Application of relativity in modern navigation[M]. Beijing: National Defend Industry Press, 2015: 176-177. (in Chinese) |



