目标跟踪是计算机视觉领域中的一个重要问题,在过去十多年中一直是计算机视觉领域中非常活跃的研究内容。目标跟踪的过程是:在初始图像帧中给出特定目标的初始状态,然后估计该目标在后续各图像帧中的状态。目标跟踪在实际生活中有广泛的应用,如人机互动、智能监控、视频检索和自动驾驶等[1-2]。目标跟踪技术尽管已经取得了很大进步,但是设计出对各种场景都能做到实时稳定跟踪的算法仍然是一项很大的挑战。这是因为实际中的场景十分复杂,跟踪过程中会遇到各种问题,例如光照变化、形态变化、尺度变化、遮挡问题以及背景相似等,这些因素使得跟踪过程不稳定,增加了跟踪难度。
最近卷积表示开始应用到目标跟踪并实现了非常好的跟踪效果,在跟踪速度和精度上都得到了很大的提升,吸引了国内外学者的关注。Bolme等利用最小输出误差平方和求解滤波器,提出MOSSE跟踪法[3],该算法是基于单通道特征多样本训练的跟踪算法,通过少量样本训练实现了高速跟踪。Henriques等提出的KCF跟踪器[4],是利用核函数矩阵的循环结构,通过核化的岭回归函数求解卷积滤波器,实现了快速的目标检测和跟踪。Danelljan等通过多通道特征单样本卷积表示求解滤波器,并将此结构应用到尺度分析上,提出了DSST跟踪算法[5],将位移和尺度上的跟踪同时进行,提高了跟踪的稳定性。
注意到大多数基于卷积的目标跟踪算法都是通过正则化约束求解卷积滤波器的近似解[5-7],对于卷积表示无正则化模型很少涉及。卷积表示无正则化模型是求解卷积表示问题的精确解,该模型经过离散傅里叶变换可以得到若干个相互独立的子问题。子问题可以通过Moore-Penrose广义逆进行求解,进而得到模型的通解,给出滤波器的一般设计算法,最后利用跟踪过程的前后连续性迭代生成滤波器,从而得到适合不同场景的滤波器。其中,广义逆可以通过满秩算法快速求解。在此基础上,提出一种在傅里叶域通过广义逆理论求解卷积表示模型的目标跟踪算法,实验结果表明该算法比部分较为先进的跟踪算法具有更好的跟踪效果。
1 Moore-Penrose广义逆矩阵定义1[8] 设A∈Cn×m,如果存在X∈Cm×n, 满足: AXA=A, XAX=X, (AX)*=AX, (XA)*=XA, 则称X是矩阵A的Moore-Penrose广义逆矩阵,记为A†。
其中:“*”表示矩阵的共轭转置。
引理1[9] 设A∈Cn×m的秩为k, 则存在列满秩矩阵L和行满秩矩阵R,使得A=LR。
定理1[8] 设A∈Cn×m, A的秩为k, 则A†=R†L†=R*(RR*)-1(L*L)-1L*
推论1 设A∈C1×m,A≠0, 则
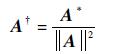
|
定理2 线性方程组Ax=b的最佳近似解为
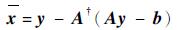
|
其中:A∈C1×m, A≠0;x∈Cm×1;b∈C;y∈Cm×1。
证明 因为Ax-b=A(x-A†b)+(AA†-I)b, 其中:A(x-A†b)和(AA†-I)b垂直。
因为
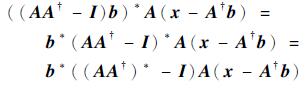
|
由广义逆的定义知
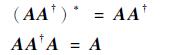
|
所以
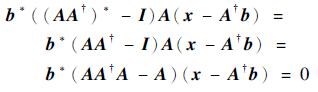
|
所以A(x-A†b)和(AA†-I)b垂直。
而(AA†-I)b=(AA†-I)(b-Ay), 由勾股定理得
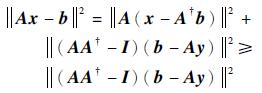
|
而
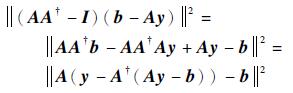
|
因此
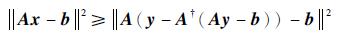
|
所以x=y-A†(Ay-b)是最佳近似解。 证毕
定理2的应用举例:求解方程3x1+5x2+2x3+7x4+x5=1。
令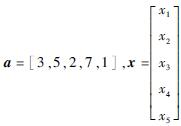
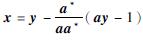
如取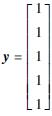
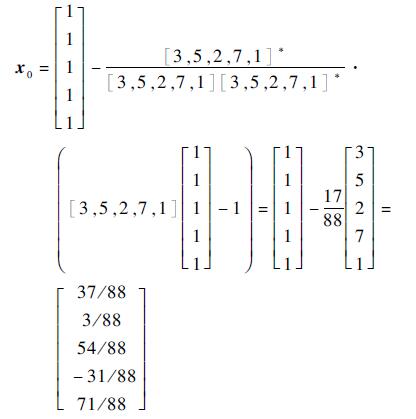
|
将此解代入方程,可以验证它为方程的解。
2 卷积表示模型卷积表示模型是用一组模板D={D1, D2, …, DK}和滤波器X={X1, X2, …, XK},通过卷积运算表示目标函数G,即
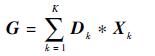
|
(1) |
式中:*为卷积符号;Dk∈RN×M;Xk∈RN×M;G∈RN×M。
由循环卷积的性质,当模板发生平移时,目标函数也会发生同样的平移,此时只需根据目标函数的最大值,即可确定目标的位置,如图 1所示。因此该模型非常适合目标运动的检测。为此,需要找到一组滤波器,使其满足式(1)。因此建立以下模型:
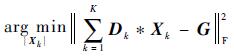
|
(2) |

|
| 图 1 响应函数预测位置 Fig. 1 Location estimation by response function |
为了便于分析和求解,该问题通常改为带正则化项的模型[5-7],即
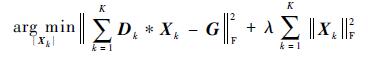
|
(3) |
式中:λ为正则化权重参数。
类似模型已经被用于目标跟踪[5]、目标检测[6]和目标配准[7]等。
正则化项是为了求得在预定条件下的确定解,这种方法便于问题的分析与求解,但是可以看出满足模型式(3)的解是原问题式(2)的近似解。为了更好地分析原问题,本文将研究无正则化项的模型式(2)。
因为卷积运算计算量特别大,而在傅里叶变换域可以转化为计算量少的点积运算,所以将该问题转到傅里叶变换域。由Parseval’s等式可知,式(2)等价于
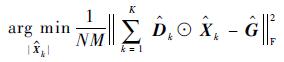
|
(4) |
式中:⊙为点积运算;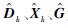
由弗罗贝尼乌斯范数的性质可知,问题式(4)等价于求解N×M个子问题
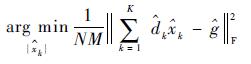
|
(5) |
式中: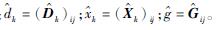
最后模型可以表示为
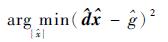
|
(6) |
式中: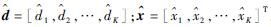
求解问题式(6)最常用的方法是通过凸优化的方法,即对优化函数求导使其等于零。但是这种方法会使得问题变得复杂,由定理2可知,该问题的最优解为
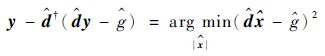
|
(7) |
在本文问题中,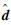
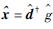
下面根据目标跟踪过程中目标特征在前后帧中相似的特点,结合滤波器的更新,给出以下设计滤波器的方法:
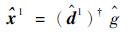
|
(8) |
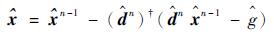
|
(9) |
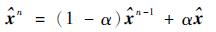
|
(10) |
式中:α为学习率。
由于
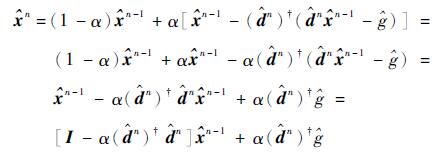
|
令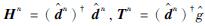
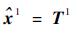
|
(11) |
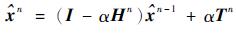
|
(12) |
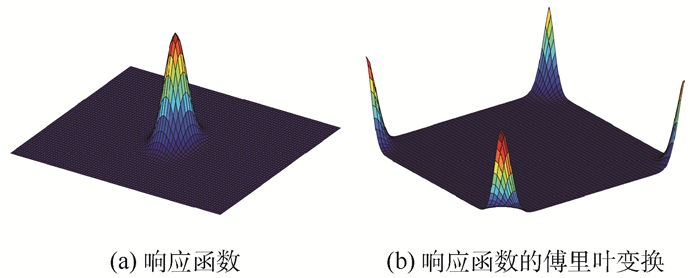
根据滤波器设计的规则可知,该算法需要求解N×M个广义逆。再对无正则化项模型进行分析,在目标跟踪过程中,问题中的G为响应函数,它是根据目标尺度确定的尖峰函数,对其做完傅里叶变换后的函数的模是一个4个顶点突起的函数,如图 2所示。分析该函数,可以发现大部分函数值的模接近零,是一个十分稀疏的矩阵。由式(8)~式(10)可知,函数值的模接近零处的滤波器系数也接近零,因此可以省去这部分滤波器的计算。离散傅里叶变换的系数具有共轭对称性[10],因此滤波器系数具有共轭对称性,因此只需要求解约一半的剩余滤波器系数。实验分析,在保证精度的条件下,需要求解的滤波器系数可以降到5%以下,大大降低了计算量。
|
| 图 2 响应函数及其傅里叶变换 Fig. 2 Response function and its Fourier transform |
本文跟踪算法如下:
1 初始化,输入初始参数
2 生成平移和尺度目标函数,并做傅里叶变换
3 输入初始帧图像F1、初始目标位置P1,提取目标特征
4 通过推论1快速求解广义逆,然后利用式(8)求解初始平移滤波器X1tran与初始尺度滤波器X1scal
5 k=2
6 重复
7 输入当前帧图像Fk,提取候选目标特征
8 由式(1)求解当前平移响应函数
9 根据平移响应函数峰值确定当前位置Pk
10 由式(1)求解当前尺度响应函数
11 根据尺度响应函数峰值确定当前尺度Sk
12 在当前位置和尺度下,提取目标特征,利用推论1快速求解广义逆,通过式(9)求解当前平移滤波器Xtran和尺度滤波器Xscal
13 由式(10)更新尺度滤波器得到Xkscal,更新平移滤波器得到Xktran
14 k=k+1
15 直到最后一帧
3 实验结果与分析本文采用DSST[5]所提出的平移-尺度跟踪框架,采用多通道特征和多尺度分析,目标特征为灰度图像和HoG特征[11],如图 3所示。利用本文提出的滤波器设计方法构建滤波器。初始化参数主要有:搜索目标范围为目标大小的4倍,尺度样本数量为33个,相邻尺度样本之间的倍数为1.015,平移滤波器学习率为0.15,尺度滤波器学习率为0.12等。本文在CPU: Inter(R) core(TM) i3-2310M 2.10GHz RAM:2G机器上进行实验。实验选取了目标跟踪基准(OTB)图像库中的32个图像序列对本文算法进行评估。这些序列包含了跟踪过程中会遇到的遮挡、尺度变化、快速运动、形变、面内旋转、面外旋转等情况,所选图像序列如图 4所示。实验结果与9个当前比较先进的跟踪算法进行对比,这些跟踪算法分别是KCF[4]、DSST[5]、SRDCF[12]、MEEM[13]、Struck[14]、ASLA[15]、SCM[16]、L1-APG[17]、CT[18]。这些算法是近年来目标跟踪领域常用来进行效果对比的算法。这些算法的跟踪结果来自OTB[19]数据库网站以及各自作者的网站。

|
| 图 3 多通道特征和多尺度采样 Fig. 3 Multi-channel features and multi-scale sampling |
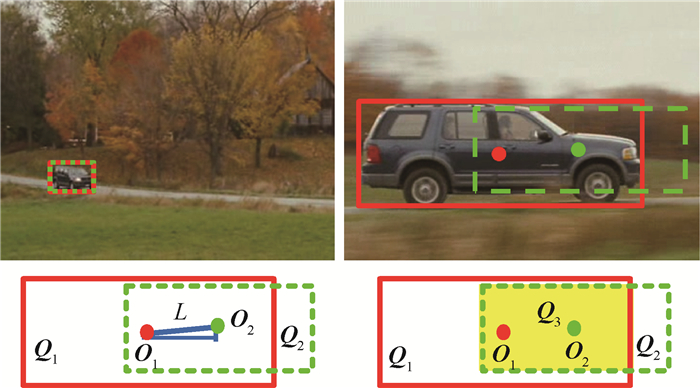
目标跟踪效果评估标准是位置误差和重叠率[19]。位置误差,即跟踪到的目标中心位置与目标实际的中心位置之间的距离。如图 5所示,O1为目标真实位置的中心点,O2为跟踪到的目标的中心点,L为真实位置的中心点与跟踪到的中心点的欧氏距离,L就是位置误差,L越小,则说明跟踪效果越好,反之越差。这种评估标准没有考虑到被跟踪目标的大小变化,当被跟踪目标大小发生变化时,这种评估标准不能很好地说明跟踪方法在估计目标大小上的性能。重叠率,即目标实际所在区域与跟踪确定目标所在区域相交的区域占相并的区域的比例,能更好地反映跟踪算法对目标的位置与大小估计。如图 5所示,Q1表示实线边框围成的区域,Q2表示虚线边框围成的区域,Q3表示阴影区域,是Q1与Q2相交的区域,重叠率为
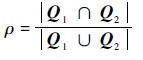
|
|
| 图 5 评估算法 Fig. 5 Evaluation algorithm |
其中:|·|表示区域的大小,即区域包含的像素数目。ρ越大,说明跟踪效果越好。
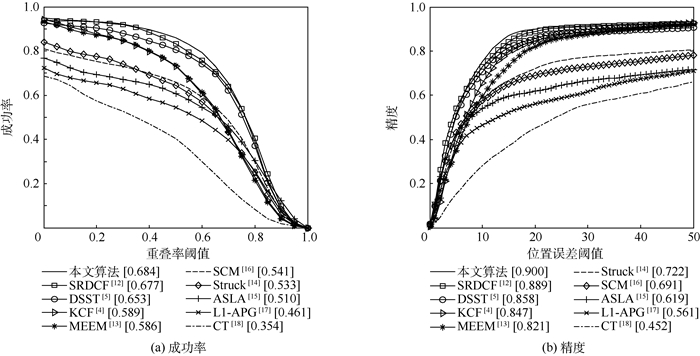
根据重叠率大于阈值的帧数占总帧数的比例可以绘制出成功率曲线图,如图 6(a)所示。根据跟踪位置误差小于阈值的帧数占总帧数的比例可以绘制出精度曲线图,如图 6(b)所示。
|
| 图 6 在32个图像序列上的成功率和精度曲线 Fig. 6 Success rate and precision curves over 32 image sequences |
图 6(a)、(b)为本文算法与KCF[4]、DSST[5]、SRDCF[12]、MEEM[13]、Struck[14]、ASLA[15]、SCM[16]、L1-APG[17]、CT[18] 10个算法在这32个图像序列上跟踪效果的综合表现,曲线反映了在不同阈值下,各跟踪算法的跟踪效果。图 6(a)中,在重叠率阈值为0.4~0.6之间,本文算法的跟踪成功率较大程度上优于其他各算法。图 6(b)中,在位置误差阈值为10~20像素之间时,本文算法的精度较大程度上优于其他各算法。依据坐标与成功率曲线围成的下边区域的面积(AUC),可对各算法进行成功率排名,图 6(a)中方括号给出了这10个算法的AUC值。依据精度曲线位置误差阈值为20像素时的精度,可对各算法进行精度排名,图 6(b)中方括号给出了这10个算法在阈值为20像素时的精度值。表 1和表 2给出了2种评估算法的排名,在这2种评估算法下,本文算法排名都是最好的,表明本文算法总体跟踪效果优于其他算法。
图 7给出了本文算法与KCF[4]、DSST[5]、MEEM[13]、Struck[14] 5个算法跟踪的跟踪效果图,其中本文算法用实线方框跟踪目标。Fleetface图像序列主要是面内旋转场景,目标人物的脸部向面内旋转,从而使目标特征发生较大变化,在690帧当人物脸部转回时,本文算法仍然能够非常好的跟踪到他的位置和大小,其他4种算法跟踪到的目标在位置和大小估计上都比较差。Soccer图像序列主要是形变场景和遮挡场景,目标球员的脸部发生较强的形变以及被前面的纸片遮挡,本文算法对目标实现持续跟踪,其他4种算法都出现丢失目标的情况。Walking2图像序列主要是尺度变化和遮挡场景,行走中的女士慢慢走向镜头的远处,从而慢慢变小,中间过程中出现男士,在一段时间内挡住了她,本文算法和DSST跟踪器都对其进行了准确的跟踪。Skating1主要是遮挡和光照变化,女生在滑行过程中被其他人部分遮挡,整个滑行场所光照发生很大变化,本文算法对其实现了稳定的跟踪。

|
| 图 7 本文算法与其他算法在Fleetface、Soccer、Walking2和Skating1序列上的跟踪结果 Fig. 7 Tracking results of proposed algorithm and other algorithms on Fleetface, Soccer, Walking2 and Skating1 sequences |
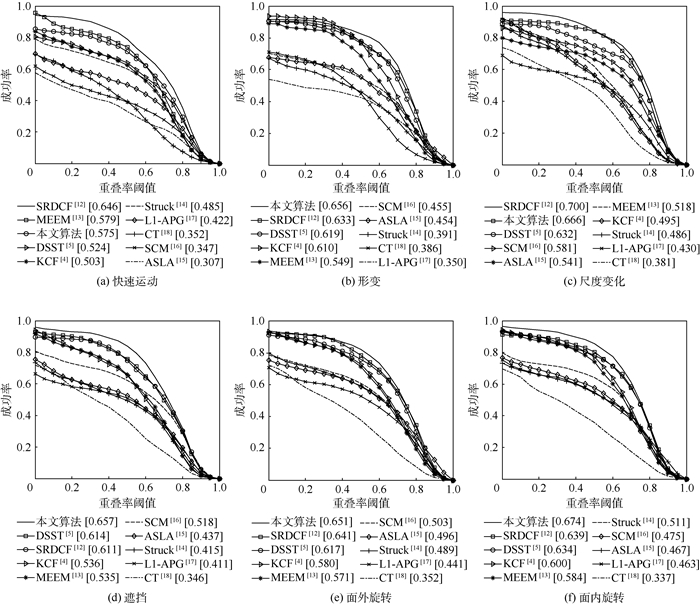
图 8为本文算法与KCF[4]、DSST[5]、SRDCF[12]、MEEM[13]、Struck[14]、ASLA[15]、SCM[16]、L1-APG[17]、CT[18] 10个算法在快速运动、形变、尺度变化、遮挡、面外旋转、面内旋转6种场景下的跟踪性能对比。图 8在各个子图中的方括号中给出了这10种跟踪器在不同场景下的AUC值。在形变、遮挡、面外旋转、面内旋转这4种场景下,本文算法的AUC值分别为0.656、0.657、0.651、0.674,均高于其他算法的AUC值,表明本文算法在这4种场景下的跟踪效果最好。在快速运动场景下,基于多样本学习的SRDCF算法的AUC值为0.646, 本文算法为0.575,这是因为SRDCF算法进行了更广区域的目标搜索,能够更好地捕捉到快速运动的目标。在尺度变化场景下,本文算法AUC值为0.666,仅次于SRDCF算法的0.700。在各种场景下,本文算法的AUC值都高于基于正则化约束的卷积表示DSST算法,表明本文所提算法提高了跟踪效果。
|
| 图 8 快速运动、形变、尺度变化、遮挡、面外旋转、面内旋转场景下的成功率曲线 Fig. 8 Success rate curves of fast motion, deformation, scale variation, occlusion, out-of-plane rotation and in-plane rotation |
本文跟踪算法在实现更好跟踪效果的同时,跟踪速度也与其他跟踪算法相近,在32个图像序列上的平均跟踪速度达到9.5帧/s,对于29像素×23像素大小的目标,可以实现26帧/s的跟踪速度,达到实时跟踪效果。跟踪算法DSST[5]、SRDCF[12]、MEEM[13]在各自文献中给出的速度分别为24、5和10帧/s。为了进一步对比速度之间的差异,将跟踪速度最快的DSST[5]跟踪算法在本文算法的实验机器上运行,得到的跟踪速度为12.3帧/s,这与本文算法的跟踪速度相近,说明了本文算法也具有较快的跟踪速度。
4 结论1) 本文提出一种在傅里叶域求解卷积表示的目标跟踪算法。将卷积表示问题变换到傅里叶域,可以通过广义逆的满秩算法快速求解,得到多样的滤波器设计方法。
2) 信号在傅里叶域的共轭对称性和稀疏性可以辅助降低算法的计算复杂度。
3) 在OTB图像库的32个序列上进行跟踪实验,与当前比较先进的9种目标跟踪算法进行对比。实验结果显示,本文跟踪算法在跟踪性能上优于其他9种跟踪算法。
后续工作会将本文提出的滤波器设计方法用于多样本训练模型,进一步提高目标跟踪的速度和精度。
| [1] | YILMAZ A, JAVED O, SHAH M. Object tracking:A survey[J]. ACM Computing Surveys, 2006, 38 (4): 1–45. |
| [2] | SMEULDERS A W M, CHU D M, CUCCHIARA R, et al. Visual tracking:An experimental survey[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2014, 36 (7): 1442–1468. DOI:10.1109/TPAMI.2013.230 |
| [3] | BOLME D S, BEVERIDGE J R, DRAPER B A, et al.Visual object tracking using adaptive correlation filters[C]//2010 IEEE Conference on Computer Vision and Pattern Recognition.Piscataway, NJ:IEEE Press, 2010:2544-2550. |
| [4] | HENRIQUES J, CASEIRO R, MARTINS P, et al. High-speed tracking with kernelized correlation filters[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 37 (3): 583–596. DOI:10.1109/TPAMI.2014.2345390 |
| [5] | DANELLJAN M, HAGER G, KHAN F S, et al.Accurate scale estimation for robust visual tracking[C]//Proceedings of the British Machine Vision Conference 2014.Durham:BMVA Press, 2014:1-11. |
| [6] | KIANI H, SIM T, LUCEY S.Multi-channel correlation filters[C]//2013 IEEE International Conference on Computer Vision.Piscataway, NJ:IEEE Press, 2013:3072-3079. |
| [7] | BODDETI N V, KANADE T, KUMAR B V K V.Correlation filters for object alignment[C]//2013 IEEE Conference on Computer Vision and Pattern Recognition.Piscataway, NJ:IEEE Press, 2013:2291-2298. |
| [8] |
张跃辉.
矩阵理论与应用[M]. 北京: 科学出版社, 2011: 207-231.
ZHANG Y H. Matrix theory and application[M]. Beijing: Science Press, 2011: 207-231. (in Chinese) |
| [9] | PUNTANEN S, STYAN P H G, ISOTALO J. Matrix tricks for linear statistical models[M]. Berlin: Springer-Verlag, 2011: 349-350. |
| [10] | OPPENHEIM V A, WILLSKY S A. Signals and systems[M]. Upper Saddle River: Prentice Hall, 1983: 322. |
| [11] | DALAL N, TRIGGS B.Histograms of oriented gradients for human detection[C]//2005 IEEE Conference on Computer Vision and Pattern Recognition.Piscataway, NJ:IEEE Press, 2005:886-893. |
| [12] | DANELLJAN M, HAGER G, KHAN S F, et al.Learning spatially regularized correlation filters for visual tracking[C]//2015 IEEE International Conference on Computer Vision.Piscataway, NJ:IEEE Press, 2015:4310-4318. |
| [13] | ZHANG J M, MA S G, SCLAROFF S.MEEM:Robust tracking via multiple experts using entropy minimization[C]//2014 European Conference on Computer Vision.Berlin:Springer-Verlag, 2014:188-203. |
| [14] | HARE S, GOLODETZ S, SAFFARI A, et al.Struck:Structured output tracking with kernels[C]//2011 IEEE International Conference on Computer Vision.Piscataway, NJ:IEEE Press, 2011:263-270. |
| [15] | JIA X, LU H C, YANG M H.Visual tracking via adaptive structural local sparse appearance model[C]//2012 IEEE Conference on Computer Vision and Pattern Recognition.Piscataway, NJ:IEEE Press, 2012:1822-1829. |
| [16] | ZHONG W, LU H C, YANG M H.Robust object tracking via sparsity-based collaborative model[C]//2012 IEEE Conference on Computer Vision and Pattern Recognition.Piscataway, NJ:IEEE Press, 2012:1838-1845. |
| [17] | BAO C L, WU Y, LING H B, et al.Real time robust L1 tracker using accelerated proximal gradient approach[C]//2012 IEEE Conference on Computer Vision and Pattern Recognition.Piscataway, NJ:IEEE Press, 2012:1830-1837. |
| [18] | ZHANG K H, ZHANG L, YANG M H.Real-time compressive tracking[C]//2012 European Conference on Computer Vision.Berlin:Springer-Verlag, 2012:866-879. |
| [19] | WU Y, LIM J, YANG M H. Object tracking benchmark[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 37 (9): 1834–1848. DOI:10.1109/TPAMI.2014.2388226 |




