在现实世界中,很多应用都面临着多目标识别问题,比如,人脸识别[1]、手写体数字识别[2]、交通指示牌识别[3]等。在模式识别领域中,对多个目标进行识别属于多类分类问题,需要设计多类分类器。现有的分类方法中,有一些可以直接应用于解决多类分类问题,比如:决策树[4]和神经网络[2]等。但其他一些成熟的、性能较好的分类方法却难以直接应用到多类分类问题中,比如:支持向量机(SVM)[5]和Adaboost[6]等,它们属于二类分类器,可以很好地解决二类分类问题。将二类分类方法扩展到多类分类领域的一种解决思路,就是采取分而治之的策略,首先将多类分类问题分解为若干个二类分类问题,然后利用二类分类方法解决二类分类问题,最后将二类分类的结果融合得到多类分类的结果。
纠错输出编码(ECOC)提供了一种通用的分解框架,可以将复杂的多类分类问题分解为一系列的二类分类问题。自1995年由Dietterich和Bakiri[7]首次提出以来,得到了众多学者的关注。近年来,有关学者还将其应用于疾病诊断领域[8-9]。在实际应用中,科研人员更关心的是ECOC的泛化能力,即ECOC对未知类别样本的预测能力。影响ECOC泛化能力的因素主要有3个:编码方法、基分类器设计和解码方法。这里的基分类器就是前面提到的二类分类器。为了提高ECOC的泛化性能,很多学者对编码方法和解码方法进行了研究。Bautista等[10]研究了基于进化算法生成编码矩阵的方法;雷蕾等[11-12]提出了基于特征空间变换的编码方法和基于支持向量数据描述的层次纠错输出编码构造方法;周进登等[13]提出利用单层感知器作为学习框架,通过学习得到编码矩阵的方法。此外,Ismailoglu等[14]研究了通过权值对分类器性能进行惩罚的加权解码方法;Passerini等[15]提出了基于后验概率的解码方法,在此基础上,周进登等[16]又将其扩展到三符号编码的解码过程中。关于编码方法和解码方法更加详细的综述可以参考文献[17]。上述研究工作从不同角度为提高ECOC的泛化性能提供了解决思路。
但科研人员对于ECOC基分类器的设计关注较少,也鲜有文献对此展开研究。2002年,Crammer和Singer[18]对现有的纠错输出编码方法进行了分析和总结,提出了3个学习问题,其中之一就是给定编码矩阵,如何找到使分类错误率最小的一组二类分类器。基分类器的设计问题就是在编码矩阵给定的前提下,如何找到一组最优的基分类器,使得ECOC的泛化误差最小。2004年,Passerini等[15]对ECOC基分类器的设计问题进行了研究,探讨了基分类器为SVM时的参数选择问题。
本文的目的就是在Passerini等[15]工作的基础上,对ECOC基分类器的设计问题开展进一步的研究,为提高ECOC的泛化性能做出一定的贡献。基分类器设计的目标是减小ECOC的泛化误差,因此,解决这一问题的关键就是如何计算ECOC的泛化误差。但由于样本的分布是未知的,ECOC真实的泛化误差往往难以计算,因此,实际中科研人员经常使用的是泛化误差的估计值。留一(LOO)误差可以看做泛化误差的一种无偏估计。但当样本的数量较大时,计算留一误差需要耗费大量的时间。一种可行的解决思路就是估计留一误差的界,利用留一误差界对ECOC的泛化性能进行估计。本文的主要工作就是给出ECOC留一误差界的估计。
同时,为了简化问题,本文也只针对基分类器为SVM时的情形进行研究。当基分类器为SVM时,其设计问题就是如何选择最优的参数问题,这些参数包括核参数和正则化参数。不同的参数下,基分类器的泛化能力不同,进而影响ECOC整体的泛化性能。另外,对于ECOC来讲,其基分类器的参数选择有2种情形:一是每个基分类器的参数不相同,需要分别为每个基分类器选择最优的参数;二是所有的基分类器的参数相同,可以同时为所有的基分类器选择最优的参数。显然,前者的难度要远大于后者。因此,本文假设所有的基分类器具有相同的参数。
本文首先介绍了ECOC框架;然后给出了ECOC留一误差的定义,从此定义出发,分别给出了ECOC留一误差的上界和下界估计;最后给出了实验结果与分析。
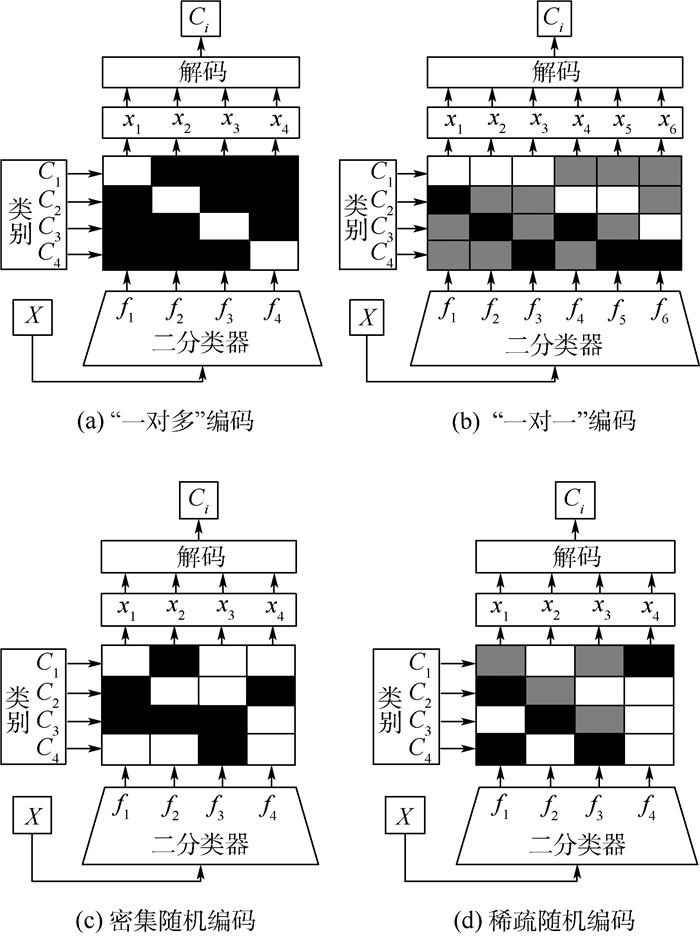
1 纠错输出编码ECOC是一种利用二元或三元的编码矩阵将多类分类问题分解为若干个二类分类问题的通用集成框架。其中,二元编码矩阵可以表示为M∈{-1, +1}k×S,k为类别数,S为编码长度,编码矩阵的行代表某一类,编码矩阵的列代表一个二类划分,“-1”表示其所在行对应的类在二类划分中被划分为负类,“+1”表示其所在行对应的类在二类划分中被划分为正类;三元编码矩阵可以表示为M∈{-1, 0, +1}k×S,其中“0”表示其所在行对应的类在二类划分中被忽略。图 1给出了4种常见的ECOC编码方法,分别是:“一对多”编码、“一对一”编码、密集随机编码、稀疏随机编码。图 1中码元“+1”、“-1”和“0”分别用白色、黑色和灰色表示。
|
| 图 1 4种常见的ECOC Fig. 1 Four commonly-used ECOCs |
ECOC解决多类分类问题时,通常可以划分为三个阶段:编码阶段、训练阶段和解码阶段。在编码阶段,形成多个二类划分,每个二类划分对应一个二类分类任务。在训练阶段,根据二类划分生成基分类器的训练数据集,完成对基分类器fs(s=1, 2, …, S)的训练。例如,在图 1(d)中对基分类器f3进行训练时,选择白色对应的C2为正类,黑色对应的C4为负类,构成训练数据集,而忽略灰色对应的类别C1和C3。
在解码阶段,根据多个基分类器的分类结果,利用某种解码规则(融合策略)得到最终的分类结果。例如,在图 1(d)给定一个测试样本X,利用训练得到的基分类器对其进行分类,结果为一码字向量(x1, x2, x3, x4)(其中xi∈{-1, +1}),根据码字向量与编码矩阵行之间的最小汉明距离得到分类结果。
2 ECOC留一误差及上下界的估计 2.1 ECOC的留一误差首先定义样本x的多分类间隔[15]:

|
(1) |
式中:
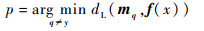
|
(2) |
my为编码矩阵行向量;f(x)为基分类器输出向量;dL(·)为线性损失函数解码。
根据ECOC的解码规则,当g(x, y) < 0时,样本x被错分;而当g(x, y)≥0时,样本x被正确分类。由此可见,根据多分类间隔g(x, y)的取值,可以对样本x是否被ECOC错误分类进行判断。进而对于训练集中的所有样本,ECOC的经验误差可以写为
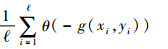
|
(3) |
式中:ℓ为训练集中样本的个数;yi为样本xi的类别; θ(·)为一函数,其定义为
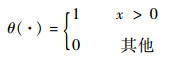
|
参考ECOC经验误差的定义,可以给出ECOC留一误差的定义。假设在留一测试过程中,样本xi是被剔除的样本。此时,剔除样本后得到的新的训练集的样本个数为ℓ-1。在新的训练集上训练ECOC,训练后得到一组基分类器,记为fi(·)。接下来利用多分类间隔对样本xi是否被ECOC错误分类进行判断。被剔除样本xi的多分类间隔记为gi(xi, yi),其定义为
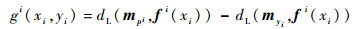
|
(4) |
式中:
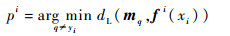
|
(5) |
同样,根据ECOC的决策规则,当gi(xi, yi) < 0时,样本xi将被错误分类;否则,样本xi将被正确分类。即根据gi(xi, yi)的取值,可以对样本xi在留一测试过程中是否会被错误分类进行判断。因此,对于训练集中的所有样本,ECOC的留一误差可以定义为
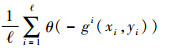
|
(6) |
通常,科研人员认为留一误差可以看作一个学习算法泛化误差的无偏估计,可以有效地指导学习算法中的参数选择。但在实际应用中,计算某一算法的留一误差的复杂度很高,时间开销很大。假设某一训练集的样本个数为ℓ,则计算某一算法的留一误差,需要对该学习算法进行ℓ次训练。特别的,当训练集中的样本数很大时,计算学习算法的留一误差成为了不可能完成的任务。因此,在解决实际问题时,科研人员经常致力于寻找留一误差的界,利用这一界值对学习算法的留一误差进行估计,进而估计该学习算法的泛化误差。
接下来,从ECOC的留一误差的定义出发,分别给出ECOC的留一误差的上界和下界。
2.2 ECOC留一误差的上界和下界估计估计ECOC留一误差的界的关键在于,如何判断被剔除样本xi在留一测试过程中是否被错误分类。这一点可以通过对多分类间隔gi(xi, yi)取值的判断来实现。当gi(xi, yi) < 0时,就可以认为样本xi在留一测试过程中被错误分类。因此,估计ECOC的留一误差界的问题就转化为估计多分类间隔gi(xi, yi)的取值问题。
为了简化问题,本文假设解码方法为线性损失函数解码,其定义为
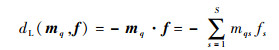
|
(7) |
此时,多分类间隔gi(xi, yi)可以写为

|
(8) |
在留一测试过程中,每剔除掉一个样本都要重新训练一次fi(·),这是导致计算留一误差时间开销比较大的主要原因。因此,为了减少计算开销,需要消除fi(·)对多分类间隔gi(xi, yi)取值的影响。幸运的是,文献[15]中的引理1建立了fi(·)与f(·)之间的联系。由于f(·)仅需要在整个训练集上训练一次,因此,如果利用f(·)代替fi(·),理论上讲,只需要在整个训练集上训练一次ECOC,就可以判断所有样本的多分类间隔gi(xi, yi)的取值。从而,大大减小计算开销。
引理1[15] 假设f为一个在整个训练集上训练得到的SVM,fi为剔除掉样本xi后在新的训练集上训练得到的SVM。则有式(9)成立:
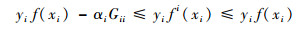
|
(9) |
式中:αi为求解优化问题得到的拉格朗日系数;Gii=K(xi, xi),K(·, ·)为核函数。
引理1的证明过程见文献[15]。将引理1应用于ECOC的每一个基分类器,不等式(9)可以重写为

|
(10) |
式中:λs∈[0, αisGiis]。
将式(10)代入多分类间隔gi(xi, yi)的定义中,可以得到

|
(11) |
这样,在多分类间隔gi(xi, yi)的定义中,消除了fi(·)的影响。但仍然需要指出的是,在式(11)中,有2个参数是无法确定的,分别是pi和λs。这2个参数的未知性,导致无法准确的得到多分类间隔gi(xi, yi)的取值。因此,本文通过对多分类间隔gi(xi, yi)的缩放,对多分类间隔gi(xi, yi)的取值进行估计,分别得到了ECOC的留一误差上界和下界。
首先,需要说明多分类间隔gi(xi, yi)的取值的缩放与ECOC留一误差上界和下界之间的联系。假设多分类间隔gi(xi, yi)的取值满足下面的不等式,或者说多分类间隔gi(xi, yi)的取值在区间[A, B]上。

|
(12) |
式中:A和B的取值是可以确定的。这样,通过A和B就可以估计多分类间隔gi(xi, yi)的取值。
当gi(xi, yi) < 0时,一定有A < 0成立;但是反之则不然,当A < 0时,不一定有gi(xi, yi) < 0成立。因此,可以得出结论,A < 0是gi(xi, yi) < 0成立的必要条件而非充分条件。进一步,如果根据A的取值对ECOC的留一误差进行估计,得到的一定是ECOC留一误差的上界,即有

|
(13) |
式中:Ai为基于样本xi计算得到的A。
另一方面,当B < 0时,一定有gi(xi, yi) < 0成立;但反之,当gi(xi, yi) < 0时,不一定有B < 0成立。因此,可以得出结论,B < 0是gi(xi, yi) < 0成立的充分条件而非必要条件。进一步,如果根据B的取值对ECOC的留一误差进行估计,得到的一定是ECOC留一误差的下界,即有

|
(14) |
式中:Bi为基于样本xi计算得到的B。
由此可以看出,如何找到合适的A和B是得到ECOC留一误差上界和下界的关键,也是本文致力于解决的问题。下面通过定理1和定理2分别给出ECOC的留一误差上界和下界。
定理1 当基分类器为SVM,解码方法为线性损失函数解码时,ECOC的留一误差上界为
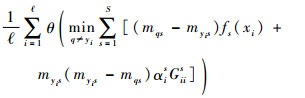
|
证明 首先考虑myis(myis-mpis)的取值。myis和mpis都有3种可能的取值,分别是+1,0和-1。
当myis=0时,myis(myis-mpis)=0。
当myis=+1时,
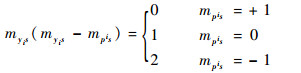
|
当myis=-1时,
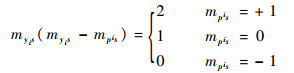
|
所以,myis(myis-mpis)的取值是非负的。同时,考虑到λs∈[0, αisGiis],则有
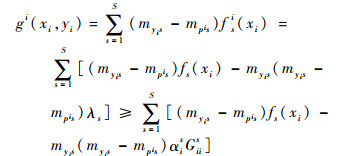
|
式中:pi与fi(·)相关,其值仍然难以确定。事实上,pi代表了编码矩阵M中的某一行。因此可得
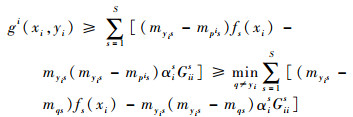
|
当gi(xi, yi) < 0时,则一定有
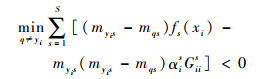
|
因此,可以得到
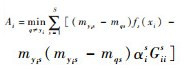
|
证毕
定理2 当基分类器为SVM,解码方法为线性损失函数解码时,ECOC的留一误差下界为
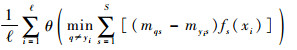
|
证明 考虑到myis(myis-mpis)和λs的非负性,则有
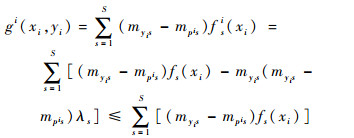
|
同样的,pi代表了编码矩阵M中的某一行。因此,则有
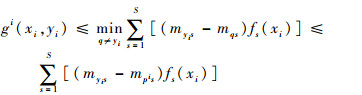
|
则当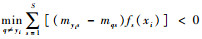
所以,可以得到
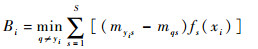
|
证毕
还需要注意的一点是,定理2给出的ECOC留一误差的下界可以进一步写为

|
(15) |
由此可以看出,ECOC留一误差的下界实际上就是ECOC的经验误差,也称为训练误差。
至此,本文分别给出了ECOC留一误差的上界和下界。下面将通过实验对这2个界的有效性进行验证。
3 实验下面从实验数据、实验设计以及实验结果与分析3个方面对实验进行介绍。
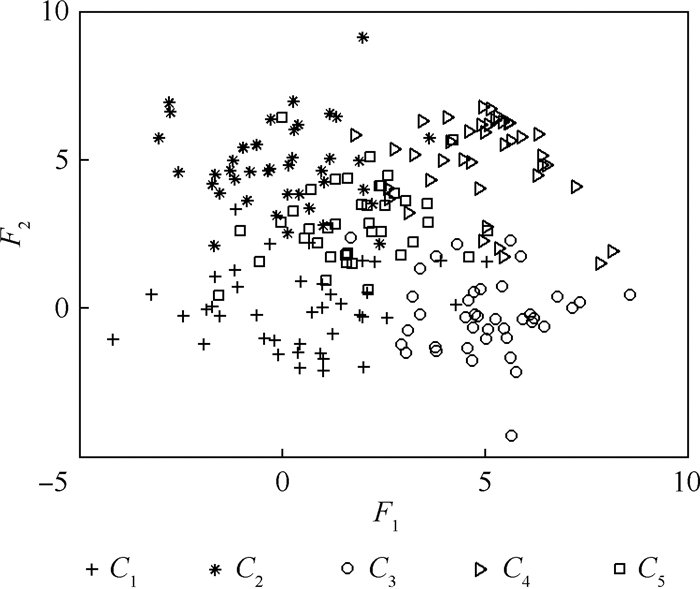
3.1 实验数据实验数据为一个人工数据集和多个UCI数据集[19]。人工数据集共包含5类样本,每一类的样本个数为50,各类的数据分布如图 2所示。每一类特征向量的维数为2,图中分别用F1和F2表示,并且服从正态分布,其概率密度函数为

|
(16) |
|
| 图 2 人工数据集的数据分布 Fig. 2 Data distribution of synthetic dataset |
式中:x为二维特征向量;μi为平均值向量;Σi为协方差矩阵;各参数的设置见表 1。
| 类别 | 先验概率 | 平均值向量 | 协方差矩阵 |
| C1 | P(C1)=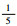 | μ1=(0, 0)T | Σ1=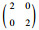 |
| C2 | P(C2)=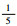 | μ2=(0, 5)T | Σ2=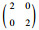 |
| C3 | P(C3)=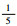 | μ3=(5, 0)T | Σ3=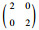 |
| C4 | P(C4)=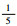 | μ4=(5, 5)T | Σ4=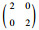 |
| C5 | P(C5)=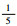 | μ5=(2, 3)T | Σ5=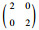 |
实验中,从UCI数据集中共选取了6个多类的数据集。表 2给出了这些数据集的样本的数目、特征量的维数以及包含类别的个数。
| 数据集 | 样本个数 | 特征维数 | 类别数 |
| vowel | 990 | 13 | 11 |
| balance | 625 | 4 | 3 |
| glass | 214 | 10 | 6 |
| vehicle | 846 | 18 | 4 |
| letter | 1 214 | 16 | 26 |
| segmentation | 2 310 | 19 | 7 |
3.2 实验设计
本实验设计的目的是为了检验定理1和定理2给出的ECOC留一误差上界和下界的有效性。留一误差界的有效性是指留一误差的上界或者下界具有与留一误差相同或者相近的变化趋势。这样,当留一误差的上界或下界减小时,能够推断出留一误差也应该相应的减小。
由于人工数据集的样本个数较少,共有200个样本,因此,在人工数据集上进行留一误差测试,统计实际的留一误差。考虑到UCI数据集的样本个数较多,进行留一误差测试耗时较长,所以,在UCI数据集上进行20重交叉验证,以交叉验证的结果来近似代替留一误差。
实验中基分类器为SVM,核函数为高斯径向基核函数。编码方法包括“一对多”编码和“一对一”编码。解码方法为线性损失函数解码。正则化参数C和核参数σ的变化范围均设置为{2-5, 2-4, …, 28}。为了简化实验,所有基分类器的正则化参数和核参数的设置相同。
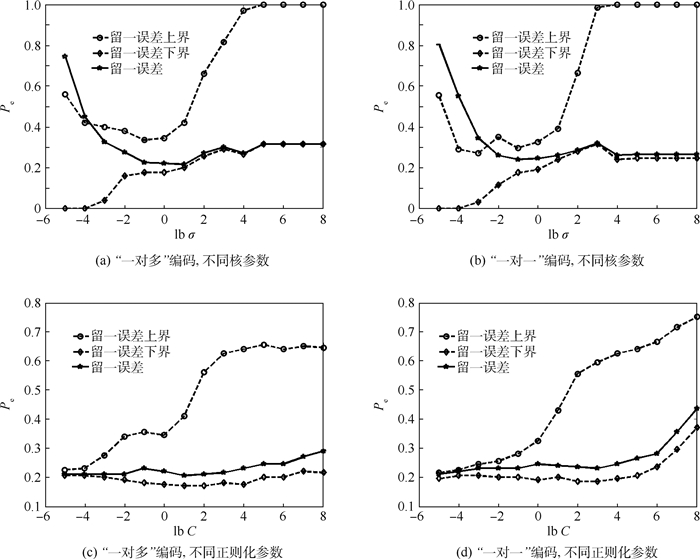
3.3 实验结果与分析 3.3.1 人工数据集图 3分别给出了不同核参数和正则化参数下的留一误差和留一误差上下界的变化情况,分类错误率为Pe。由图 3可以看出,留一误差随着这2个参数的变化起伏较大,这证明了通过对正则化参数和核参数进行优化,可以有效地提高ECOC的泛化性能。对比图 3(a)、(b)和图 3(c)、(d)中留一误差变化曲线的起伏程度可知,核参数对ECOC的留一误差的影响要大于正则化参数的影响。这说明,对核参数进行优化对于提高ECOC的泛化性能更加重要。
|
| 图 3 人工数据集上不同核参数和正则化参数对应的留一误差和留一误差上下界 Fig. 3 LOO error and LOO error's upper and lower bounds with different kernel parameters andregularization parameters on synthetic dataset |
由图 3还可以看出,留一误差上界最小值出现的位置与留一误差最小值出现的位置非常接近。因此,利用留一误差上界可以指导本文选择最优的核参数和正则化参数。可以说,定理1给出的留一误差的上界是有效的。同时,还需要说明的是,定理1中留一误差上界的计算仅需要将分类器在训练集上训练一次,不需要增加额外的计算代价。
但是,图 3(a)、(b)中留一误差下界最小值出现的位置却与留一误差最小值出现的位置偏差很大。这说明,留一误差的下界是不能有效地指导选择最优参数。应该注意到,定理2给出的留一误差下界实际上就是ECOC的训练误差。这也就从另一个角度验证了最小化训练误差并不一定能够最小化泛化误差。
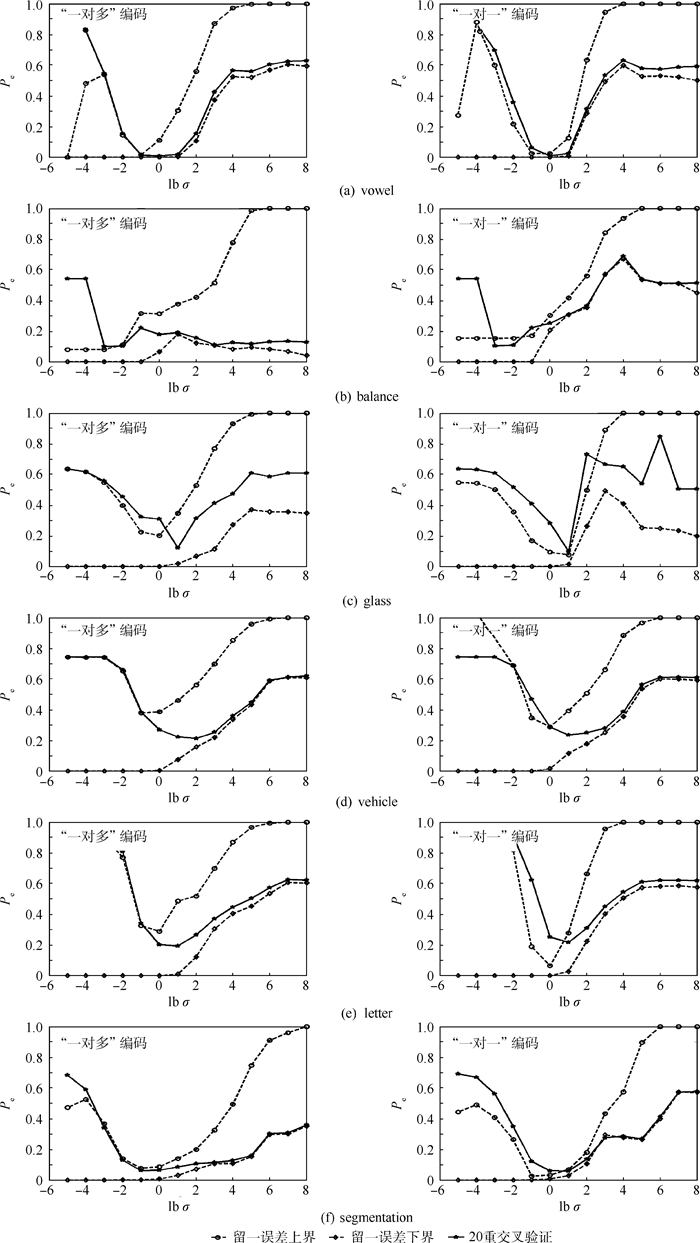
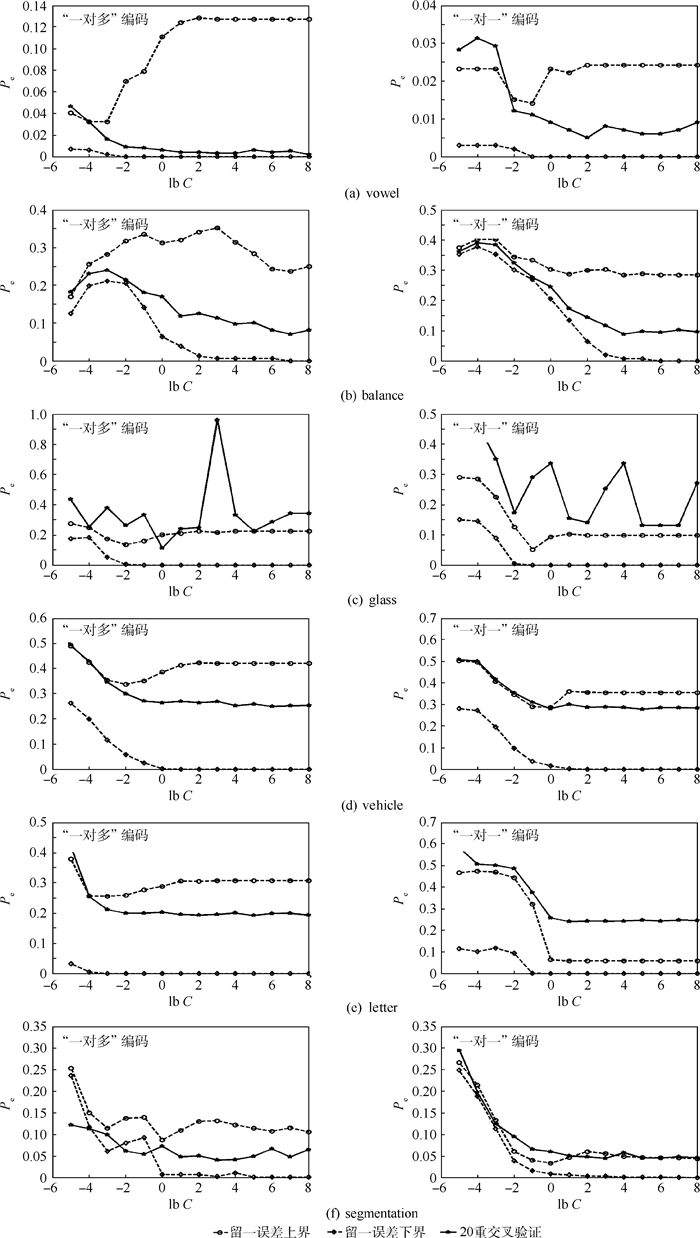
3.3.2 UCI数据集图 4和图 5分别给出了UCI数据集上不同核参数和正则化参数下20重交叉验证的结果及留一误差上下界的变化情况。由图中可以看出,根据留一误差上界的最小值可以找到一个相对较小的20重交叉验证结果。图中尽管留一误差上界的最小值与20重交叉验证结果最小值之间存在一定的偏差,但根据留一误差上界最小值对参数进行择优仍然可以很大程度上提高分类器的泛化能力。因此,可以说,在UCI数据集上定理1给出的留一误差上界仍然可以有效地指导核参数和正则化参数的选择。
|
| 图 4 UCI数据集上不同核参数下20重交叉验证的结果及留一误差上下界 Fig. 4 20-fold cross validation results and LOO error's upper and lower bound withdifferent kernel parameters on UCI datasets |
|
| 图 5 UCI数据集上不同正则化参数下20重交叉验证的结果及留一误差上下界 Fig. 5 20-fold cross validation results and LOO error's upper and lower bound withdifferent regularization parameters on UCI datasets |
另一方面,从图 4中可以看到,20重交叉验证结果的最小值和留一误差上界的最小值几乎都出现在了留一误差下界等于0的位置上,也就是训练误差为0的位置。这似乎可以说明最小化训练误差是最小化泛化误差的必要条件,但非充分条件。更有趣的现象是,图 3(c)、(d)和图 5中在不同的正则化参数下,与留一误差上界相比,留一误差下界具有与留一误差或者20重交叉验证结果更加相似的变化趋势。并且,在图 3(a)、(b)和图 4中,当核参数取值较大时,留一误差上界都出现了完全收敛于留一误差或者20重交叉验证结果的现象。由于知识积累的不足,现阶段本文无法对上述现象给出合理的解释,也无法对定理2给出的留一误差下界在ECOC模型选择中的应用给出准确的说明。但文献[20]已经指出,泛化误差界的下界估计可以提供经验风险收敛于期望风险的本质属性,从而可以更本质的判别学习算法的性能。因此,未来对ECOC的留一误差下界进行深入的研究将是一项富有意义的工作。
4 结论1) 本文给出的ECOC留一误差的上界可以有效地指导基分类器参数的选择,其中,对核参数的优化重要性更大。
2) 通过为基分类器选择最优的参数,可以有效地提高ECOC的泛化性能。
3) ECOC的经验误差或者说训练误差可以作为ECOC留一误差的下界。
4) 本文给出的ECOC留一误差的下界在某些情况下可以完全收敛于真实的留一误差。
未来为了提高对ECOC泛化能力的估计精度,需要对ECOC留一误差的下界进行更加深入的研究。此外,当每个基分类器的参数不相同时,研究ECOC的基分类器的设计问题也是一项富有挑战性的工作。探讨其它解码方法下的ECOC留一误差界的估计也可以作为未来的一个研究方向。
| [1] | NI J, XU X Z, DING S F, et al. An adaptive extreme learning machine algorithm and its application on face recognition[J]. International Journal of Computing Science and Mathmatics, 2015, 6 (6): 611–619. DOI:10.1504/IJCSM.2015.073601 |
| [2] | QURESHI M S, QURESHI M B, NABI M G, et al. Handwritten digit recognition system using neural network[J]. Energy Procedia, 2011, 13 : 4326–4336. DOI:10.1016/S1876-6102(14)00454-8 |
| [3] | BERKAYA S K, GUNDUZ H, OZSEN O, et al. On circular traffic sign detection and recognition[J]. Expert System with Applications, 2016, 48 : 67–75. DOI:10.1016/j.eswa.2015.11.018 |
| [4] | NITHYA R, SANTHI B. Decision tree classifiers for mass classification[J]. International Journal of Signal and Imaging System Engineering, 2015, 8 (1/2): 39–45. DOI:10.1504/IJSISE.2015.067068 |
| [5] |
边肇祺, 张学工.
模式识别[M]. 2版 北京: 清华大学出版社, 2000: 296-303.
BIAN Z Q, ZHANG X G. Pattern recognition[M]. 2nd ed Beijing: Tsinghua University Press, 2000: 296-303. (in Chinese) |
| [6] | FREUND Y, SHAPIRE R E. A decision-theoretic generalization of online learning and an application to boosting[J]. Journal of Computer and System Sciences, 1997, 55 (1): 119–139. DOI:10.1006/jcss.1997.1504 |
| [7] | DIETTERICH T G, BAKIRI G. Solving multiclass learning problems via error-correcting output codes[J]. Journal of Artificial Intelligence Research, 1995, 2 (1): 263–286. |
| [8] | BAI X L, NIWAS S I, LIN W S, et al. Learning ECOC code matrix for multiclass classification with application to glaucoma diagnosis[J]. Journal of Medical Systems, 2016, 40 (4): 78. DOI:10.1007/s10916-016-0436-2 |
| [9] | LIU K H, ZENG Z H, NG V T Y. A hierarchical ensemble of ECOC for cancer classification based on multi-class microarray data[J]. Information Sciences, 2016, 349-350 : 102–118. DOI:10.1016/j.ins.2016.02.028 |
| [10] | BAUTISTA M A, ESCALERA S, BARO X, et al. On the design of an ECOC-compliant genetic algorithm[J]. Pattern Recognition, 2014, 47 (2): 865–884. DOI:10.1016/j.patcog.2013.06.019 |
| [11] |
雷蕾, 王晓丹, 罗玺, 等. 基于特征空间变换的纠错输出编码[J].
控制与决策, 2015, 30 (9): 1597–1602.
LEI L, WANG X D, LUO X, et al. Error-correcting output codes based on feature space transformation[J]. Control and Decision, 2015, 30 (9): 1597–1602. (in Chinese) |
| [12] |
雷蕾, 王晓丹, 罗玺, 等. 基于SVDD的层次纠错输出编码研究[J].
系统工程与电子技术, 2015, 37 (8): 1916–1921.
LEI L, WANG X D, LUO X, et al. Hierarchical error-correcting output codes based on SVDD[J]. Systems Engineering and Electronics, 2015, 37 (8): 1916–1921. DOI:10.3969/j.issn.1001-506X.2015.08.30 (in Chinese) |
| [13] |
周进登, 周红建, 杨云, 等. 基于神经网络的纠错输出编码方法研究[J].
电子学报, 2013, 41 (6): 1114–1121.
ZHOU J D, ZHOU H J, YANG Y, et al. Coding design for error correcting output codes based on neural network[J]. Acta Electronica Sinica, 2013, 41 (6): 1114–1121. (in Chinese) |
| [14] | ISMAILOGLU F, SPRINGHUIZEN I G, SMIRNOV E, et al. Fractional programming weighted decoding for error-correcting output codes[J]. Lecture Note in Computer Science, 2015, 9132 : 38–50. DOI:10.1007/978-3-319-20248-8 |
| [15] | PASSERINI A, PONTIL M, FRASCONI P. New results on error correcting output codes of kernel machines[J]. IEEE Transactions on Neural Networks, 2004, 15 (1): 45–54. DOI:10.1109/TNN.2003.820841 |
| [16] | ZHOU J D, WANG X D, ZHOU H J, et al. Decoding design based on posterior probabilities in ternary error-correcting output codes[J]. Pattern Recognition, 2012, 45 (4): 1802–1818. DOI:10.1016/j.patcog.2011.10.009 |
| [17] |
雷蕾, 王晓丹, 罗玺, 等. ECOC多类分类研究综述[J].
电子学报, 2014, 42 (9): 1794–1800.
LEI L, WANG X D, LUO X, et al. An overview of multi-classification based on error-correcting output codes[J]. Acta Electronica Sinica, 2014, 42 (9): 1794–1800. (in Chinese) |
| [18] | CRAMMER K, SINGER Y. On the learnability and design of output codes for multiclass problems[J]. Machine Learning, 2002, 47 (2-3): 201–233. |
| [19] | ASUNCION A, NEWMAN D. UCI machine learning repository[D]. Irvine: University of California, 2007. |
| [20] |
张海, 徐宗本. 学习理论综述(Ⅰ):稳定性与泛化性[J].
工程数学学报, 2008, 25 (1): 1–9.
ZHANG H, XU Z B. A survey on learning theory(Ⅰ):Stability and generalization[J]. Chinese Journal of Engineering Mathematics, 2008, 25 (1): 1–9. (in Chinese) |



