2. 海军航空工程学院 控制工程系, 烟台 264001;
3. 山东南山国际飞行有限公司, 烟台 265713
2. Department of Control Engineering, Naval Aeronautical and Astronautical University, Yantai 264001, China;
3. Shandong Nanshan International Flight Co., Ltd., Yantai 265713, China
近年来,协同制导问题引起了越来越多学者的研究兴趣。文献[1-2]研究了多枚反舰导弹的协同制导问题,以期有效突破近程防御武器系统。李新三等[3]针对带有末端攻击角度约束的多导弹协同制导问题,运用模型预测扩展控制和协同比例制导,设计了一种满足末端攻击角度约束的多导弹协同次优制导律。孙雪娇等[4]针对多枚导弹三维空间协同攻击机动目标问题,提出了一种多导弹分布式协同制导与控制算法。赵启伦等[5]针对多导弹协同拦截高超声速目标问题,设计了一种具有领弹—从弹拓扑结构的异类导弹协同制导律。为了实现导弹的同时到达导引,必须精确估计剩余飞行时间(time-to-go),已有学者提出了一些可以借鉴的算法。
Tahk等[6]提出了一种递推的剩余时间预测算法,但其剩余时间估计误差较大。Lam[7]推导出了2种计算剩余时间的闭环解析解,但其假设条件比较理想。Ryoo等[8]针对最优导引律/攻击角度控制-0型(OGL/IAC-0) 导引律,提出了一种估计剩余时间的算法,但难以满足时间控制的精度要求。Whang和Ra[9-10]对比例导引律情况,提出了一种基于Kalman滤波的剩余时间估计算法;另外,对偏置比例导引律情况,推导出了一种剩余时间估计滤波器,但该算法不适用于初始前置角较大的情况。Shin等[11]应用导引指令历史数据提出了一种剩余时间估计算法,但其计算量较大。Cho和Ryoo[12]针对速度变化规律具有一定不确定性的导弹,推导出了一类加权能量最优导引律,对导弹未来速度曲线进行了预测,对剩余时间进行了估计,但其估计精度难以满足时间控制要求。李辕等[13]分别针对顺轨与逆轨拦截飞行轨迹的特点,基于预测碰撞点设计了相应的剩余飞行时间估计算法。但上述算法在导弹前置角较大时估计精度都不高。
针对现有剩余时间估计算法在导弹前置角较大时估计精度不高的问题,笔者课题组[14]提出了一种采用分段求解的比例导引剩余时间估计算法,该算法首先对比例导引的闭环运动方程进行变形,得到弹目距离和飞行时间关于前置角的一阶非线性微分方程,然后对前置角的变化区间适当分段,在每段区间内保证前置角的增量为小角度,从而利用一阶泰勒展开求解每段区间内的微分方程,最后通过分段迭代求解,得到大前置角下的剩余时间估计。另外,笔者课题组[15]构造了一种带攻击角度约束项并考虑前置角约束的偏置比例导引律,并且采用分段求解的思想给出了对应的剩余时间估计算法。
文献[14-15]中提出的剩余时间估计算法,虽然适合于解决大前置角情况下的剩余时间估计问题,但其算法假设导弹飞行速度大小为已知常值,而这与实际情况并不相符合,因为实际导弹的飞行速度根本就不进行控制,在导弹速度时变情况下,如何解决大前置角情况下的剩余时间估计问题目前还没有解决。本文针对该问题给出了一种解决算法。相比于文献[14-15],本文的主要贡献在于增加了对导弹时变速度的预测,并基于此,给出了在导弹速度时变且考虑大前置角的情况下比例导引律和偏置比例导引律的剩余时间估计算法。
1 问题描述考虑如图 1所示的寻的制导,XOY为地面坐标系,目标静止,导弹速度大小V(t)时变,M为导弹,T为目标。R、q、θ与φ分别为惯性系下的弹目距离、目标视线角、导弹的航向角与前置角。导引方程可表示为

|
(1) |

|
| 图 1 寻的制导示意图 Fig. 1 Schematic diagram of homing guidance |
式中:an为导引指令。初始条件为R(t0)=R0,φ(t0)=φ0,q(t0)=q0,θ(t0)=θ0。
要解决的问题是:在考虑导弹的飞行速度大小时变的情况下,如何采用分段迭代的思想估计出大前置角下采用比例导引律和偏置比例导引律的剩余时间。
2 比例导引律的剩余时间估计 2.1 闭环形式的反舰导弹速度方程文献[14]在假定导弹速度大小恒定的情况下,采用分段求解算法,依据t0时刻的初始条件,通过求解式(1),得到了t0+Δt时刻的分段解为

|
(2) |

|
(3) |

|
(4) |
式中:N为比例导引系数;Δφ1=Δφ(t0+Δt)。
依据文献[14]的分段迭代算法,假定当前被处理的分割段[t0, t0+Δt]内导弹速度大小恒定,由分割段起点处的φ(t0)、R(t0),可得到分割段末端处的φ(t0+Δt)、R(t0+Δt)以及导弹飞过该分割段所需时间Δt。由比例导引律有
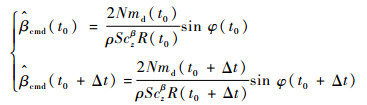
|
(5) |
式中:下标“cmd”表示指令。
考虑到平飞是反舰导弹的典型飞行状态,其速度方程可描述为

|
(6) |
式中:P(t)为推力;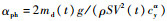
将式(5) 代入式(6),即得闭环形式的反舰导弹速度方程。
2.2 剩余时间估计算法结合文献[14]的分段迭代算法和闭环形式的反舰导弹速度方程,对导弹速度大小进行分段迭代预测,并对剩余时间进行估计与更新,步骤如A1)~G1) 所示:
A1) 将当前时刻测得的R、q、θ作为估算当前时刻剩余时间tgo的估计值


B1) 当
C1) 当



D1) 以当前被处理的分割段的起点处导弹的飞行速度作为该分割段的飞行速度(即认为该分割段飞行速度的大小为已知常值),求出该分割段末端处的对应状态变量,即由式(4) 解算Δt,由式(3) 解算φ(t0+Δt),由式(2) 解算R(t0+Δt),转A2)。
E1) 
F1) 转A3)。
G1) 
在转弯平飞段对导弹未来速度的大小进行预测及对剩余时间进行修正的计算步骤如A2)~ C2) 所示:
A2) 假设在当前被处理的分割段[t0, t0+Δt]内,导弹的速度是匀加速或者匀减速变化的。由V(t0)和







B2) 计算分割段[t0, t0+Δt]内的平均速度
C2) V(t0)←V(t0+Δt),迭代次数更新ck←ck+1,转E1)。
在近似直线飞行段对导弹未来速度的大小进行预测及对剩余时间进行修正的计算步骤如A3)~E3) 所示:
A3) 当



B3) 根据选定的航程长度ΔL对L(t0)进行分割,计算
C3) 如果n=1,转E3);否则,计算










D3) 
E3) 这一步对应于近似直线飞行段的最后一个分割段[L, 0]。计算









采用文献[15]构造的带攻击角度约束项并考虑前置角约束的偏置比例导引律

|
(7) |
式中:θd为期望的攻击角度;为节省篇幅,其他有关公式与符号说明可参见文献[15]。
类似于比例导引律的情况,可得当前分割段偏置比例导引律(式(7))对应的β的预测值为

|
(8) |
式中:αs=θ-Nq+(N-1)θd为文献[15]为了表述简洁而定义的一个组合角度,为了避免与前面提到的导弹迎角α混淆,特加入下标s。
类似地可写出
结合文献[15]的分段迭代算法,考虑导弹速度的时变特性,对导弹速度大小进行预测,并对剩余时间进行估计与更新的算法如a1)~g1) 所示:
a1) 令

b1) 若αs, 0≠0,转c1);否则,算法结束。
c1) 按文献[15]中的公式确定α1和Δt。
d1) 按文献[15]中的公式分别计算

e1) 若α1≠0,转a2);否则,转a3)。
f1) 



g1) 
在转弯平飞段,对导弹未来速度的大小进行预测及对剩余时间进行修正的步骤如a2)~b2) 所示:
a2) 与比例导引情况下通过分段迭代算法对导弹未来速度的大小进行预测的计算步骤基本相同,不同之处在于计算
b2) 计算分割段[t0, t0+Δt]内的平均速度V=0.5(V(t0)+V(t0+Δt));由于文献[15]确定Δt的式中只有B6=R0/(KVcos φ0)与速度有关,因此,时间更新为Δt←(V/V(t0))Δt;更新Δt后,按照a2) 的过程计算V(t0+Δt),


在近似直线飞行段,对导弹未来速度的大小进行预测及对剩余时间进行修正的步骤如a3)~e3) 所示:
a3) 当分段迭代算法中的α1=0 时,表示转弯平飞段基本结束、开始转入近似直线飞行段,通过转弯平飞段的计算,已经得到了这时的 t 0、V ( t 0)、φ(t0)、R(t0)和 αs (t0)。进一步由式(8) 可算出


|
式中:C1=1/[2(2N-1)];C2=K/[(N+K)(2N-1)];C3=K2/[(2N-1)(1+2K)(N+K)];L0←L(t0)。
b3) 根据选定的用于分段的一个固定的航程长度ΔL对L(t0)进行分割,计算
c3) 如果n=1,转e3),否则,可仿照比例导引律情况下的步骤C3),计算出t0+Δt时刻导弹速度的一个校正预测值V(t0+Δt)=V(t0)+ 
d3) 
e3) 这一步对应于近似直线飞行段的最后一个分割段[L, 0],可仿照比例导引律情况下的步骤E3),计算出t0+Δt时刻导弹速度的一个校正预测值V(t0+Δt)=V(t0)+ 

假设导弹的初始坐标为(-10 000, 0) m,初始航向角为θ(t0)=θ0=-85°,初始速度为V =300 m/s。目标静止,坐标为(0, 0) m。取N=3,ρ=1.225 kg/m3,S=0.25 m2,升力系数对迎角的偏导数为cyα=30.5 rad-1,侧力系数对侧滑角的偏导数为czβ=15.2 rad-1,重力加速度g=9.8 m/s2。以末制导开始时刻t0=0为计时起点,取导弹在末制导开始时的初始质量为M0=1 500 kg,燃料的消耗率为μ=0.5 kg/s,取阻力系数Cx≈0.33+3.8|α|+1.5|β|(迎角和侧滑角的单位为rad),推力P(t)=6 500 N。
对于比例导引律情况, 取对大前置角进行分割的角度Ω=10°,取对近似直线飞行段进行分割的长度ΔL=1 000 m。取仿真步长为0.01 s, 仿真结束条件为R < 2.5 m。仿真结果见图 2, 

|
| 图 2 比例导引律情况仿真结果 Fig. 2 Simulation results for proportional navigation guidance law |
对带攻击角度约束项并考虑前置角约束的偏置比例导引律情况, 仿真条件与仿真过程与比例导引律下的基本相同,只是增加了终端落角约束条件θ(tf)=θd=120°,tf为指定的攻击时间。仿真结果见图 3。

|
| 图 3 偏置比例导引律情况仿真结果 Fig. 3 Simulation results for biased proportional navigation guidance law |
图 2(a)、图 3(a)中还给出了常用的基于小角度假设算法[1-2]和现有的分段迭代算法[14-15]的仿真结果,以便于对剩余时间估计精度进行比较。
从图 2(a)、图 3(a)可以看出,实际的剩余时间tgo是斜率为-1的直线(即图 2(a)、图 3(a)中处于最上面的虚划线),基于速度预测的分段迭代算法的剩余时间估计曲线几乎与实际的剩余时间曲线重合, 图 2(a)的局部放大图如图 2(b)所示,其剩余时间估计误差的最大绝对值不超过0.1 s(最大估计误差出现在t=0处),显示出非常高的估计精度,而现有分段迭代算法的剩余时间估计误差却明显偏大。由于图 3(a)的局部放大图与图 2(a)的局部放大图情况类似,为简洁起见,在此从略。
仿真结果表明,在导弹飞行速度大小为时变的情况下,在典型仿真背景下,不管是采用比例导引体,还是采用带角度控制的偏置比例导引律,
采用本文提出的基于速度预测的分段迭代剩余时间估计算法的估计精度相对于现有的分段迭代剩余时间估计算法的估计精度都有非常显著提高。
5 结论1) 将分段迭代求解的思想扩展到对导弹的时变速度进行分段预测。
2) 分别给出了适用于导弹速度时变情况的大前置角下比例导引律和偏置比例导引律的剩余时间估计算法。
3) 该算法以现有分段迭代算法为基础,依据闭环形式的反舰导弹速度微分方程,分转弯平飞段和近似直线飞行段2种情况,分别对导弹未来速度的大小进行预测并对剩余时间进行修正。
4) 算法中给出了偏置比例导引律作用下近似直线飞行段剩余飞行航程的估计公式。
5) 计算结果表明,在导弹飞行速度大小为时变的情况下,不管是采用比例导引律,还是采用带角度控制的偏置比例导引律,该算法得到的剩余时间估计精度相对于现有分段迭代剩余时间估计算法的估计精度都有非常明显的提高。
| [1] | JEON I S, LEE J I, TAHK M J. Impact-time-control guidance law for anti-ship missiles[J]. IEEE Transactions on Control Systems Technology, 2006, 14 (2): 260–266. DOI:10.1109/TCST.2005.863655 |
| [2] | JEON I S, LEE J I, TAHK M J. Homing guidance law for cooperative attack of multiple missiles[J]. Journal of Guidance, Control, and Dynamics, 2010, 33 (1): 275–280. DOI:10.2514/1.40136 |
| [3] |
李新三, 汪立新, 王明建, 等. 基于MPSC和CPN制导方法的协同制导律[J].
北京航空航天大学学报, 2016, 42 (9): 1857–1863.
LI X S, WANG L X, WANG M J, et al. Cooperative guidance law based on MPSC and CPN guidance method[J]. Journal of Beijing University of Aeronautics and Astronautics, 2016, 42 (9): 1857–1863. (in Chinese) |
| [4] |
孙雪娇, 周锐, 吴江, 等. 多导弹分布式协同制导与控制方法[J].
北京航空航天大学学报, 2014, 40 (1): 120–124.
SUN X J, ZHOU R, WU J, et al. Distributed cooperative guidance and control for multiple missiles[J]. Journal of Beijing University of Aeronautics and Astronautics, 2014, 40 (1): 120–124. (in Chinese) |
| [5] |
赵启伦, 陈建, 董希旺, 等. 拦截高超声速目标的异类导弹协同制导律[J].
航空学报, 2016, 37 (3): 936–948.
ZHAO Q L, CHEN J, DONG X W, et al. Cooperative guidance law for heterogeneous missiles intercepting hypersonic weapon[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37 (3): 936–948. (in Chinese) |
| [6] | TAHK M J, RYOO C K, CHO H J. Recursive time-to-go estimation for homing guidance missiles[J]. IEEE Transactions on Aerospace and Electronic Systems, 2002, 38 (1): 13–24. DOI:10.1109/7.993225 |
| [7] | LAM V C. Time-to-go estimate for missile guidance:AIAA-2005-6459[R].Reston:AIAA, 2005. |
| [8] | RYOO C K, CHO H J, TAHK M J. Time-to-go weighted optimal guidance with impact angle constraints[J]. IEEE Transactions on Control Systems Technology, 2006, 14 (3): 483–492. DOI:10.1109/TCST.2006.872525 |
| [9] | WHANG I H, RA W S.Time-to-go estimation filter for anti-ship missile application[C]//SICE Annual Conference. Piscataway, NJ:IEEE Press, 2008:247-250. |
| [10] | WHANG I H, RA W S.Time-to-go estimator for missiles guided by BPNG[C]//International Conference on Control, Automation and Systems.Piscataway, NJ:IEEE Press, 2008:463-467. |
| [11] | SHIN H S, CHO H S, TSOURDOS A.Time-to-go estimation using guidance command history[C]//Proceedings of the 18th IFAC World Congress.Laxenburg:IFAC Secretariat, 2011:5531-5536. |
| [12] | CHO H J, RYOO C K. Implementation of optimal guidance laws using predicted missile velocity profiles[J]. Journal of Guidance, Control, and Dynamics, 1999, 22 (4): 579–588. DOI:10.2514/2.4420 |
| [13] |
李辕, 赵继广, 白国玉, 等. 基于预测碰撞点的剩余飞行时间估计方法[J].
北京航空航天大学学报, 2016, 42 (8): 1667–1674.
LI Y, ZHAO J G, BAI G Y, et al. Method of time-to-go estimation based on predicted crack point[J]. Journal of Beijing University of Aeronautics and Astronautics, 2016, 42 (8): 1667–1674. (in Chinese) |
| [14] |
张友安, 马国欣. 大前置角下比例导引律的剩余时间估计算法[J].
哈尔滨工程大学学报, 2013, 34 (11): 1409–1414.
ZHANG Y A, MA G X. Time-to-go estimation algorithm for the proportional navigation guidance law with a large lead angle[J]. Journal of Harbin Engineering University, 2013, 34 (11): 1409–1414. (in Chinese) |
| [15] | ZHANG Y A, MA G X, WU H L. A biased proportional navigation guidance law with large impact angle constraint and the time-to-go estimation[J]. Proceedings of the Institution of Mechanical Engineers, Part G:Journal of Aerospace Engineering, 2014, 228 (10): 1725–1734. DOI:10.1177/0954410013513754 |



