空气系统是保证发动机正常工作的重要组成部分,主要承担发动机冷却、封严、轴向力调整等任务。由于空气系统内部结构复杂,往往有大量的腔室和节流元件等结构,其内部的流动也比较复杂。发动机快速机动过程中的瞬时载荷[1]或运行过程中出现突发性失效,都可能造成空气系统内出现强瞬态过程,此时容腔的容积效应以及内部流动的复杂性,可能诱发短时的危险过渡态载荷,给发动机的安全性带来隐患[2]。因此,为了保证发动机过渡过程的安全性,需要在原有稳态网络法基础上,建立瞬态网络模型对空气系统的瞬态响应过程进行仿真。
当前对于瞬态空气系统低维建模的研究中,开始考虑了腔室结构的容积效应对空气系统瞬态响应的影响[3-4]。但是对于小孔结构,由于其结构尺度较小,通常认为其流动没有明显的瞬态效应,因此在瞬态空气系统低维模型中,孔结构采用稳态特性处理[5]。但是在处理瞬态空气系统过程中,还没有对孔与腔结构进行单独的部件瞬态响应研究,瞬态腔体的低维特性与稳态孔的低维特性耦合过程中可能产生较大的误差。本文建立了带前腔的旋转孔CFD计算模型和基于稳态孔特性的孔腔系统瞬态1-D模型,重点研究以旋转孔为出口的容腔的瞬态响应过程。通过计算2种瞬态边界条件的瞬态响应过程,得到了瞬态1-D模型与CFD计算模型的结果对比,发现瞬态过程中,瞬态1-D模型整体上与CFD的结果相吻合,说明采用稳态孔特性建立低维瞬态模型的思路基本可行,但是孔在瞬态过程中的进气条件相对于稳态有一定的区别,当腔内流动出现较为强烈的瞬态效应时,可使孔的进气条件出现较大变化,此时采用集总方式处理的腔无法为旋转孔提供准确的进口条件,导致瞬态1-D模型的仿真结果会有短时的较大误差,当该误差不满足工程要求时,则需要对瞬态1-D模型进行进一步的优化。
1 孔特性处理方法当前对于孔特性的研究,常采用流量系数描述孔的流动特性,其定义为孔实际流量与理论流量之比[6]:
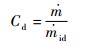
|
(1) |
式中: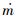
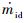
实际流量由试验测量所得,理论流量由一维等熵绝热方程计算获得,计算公式为
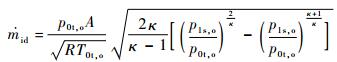
|
(2) |
式中:R为气体常数;κ为气体比热比;T0t, o为孔进口总温;p0t, o为孔进口总压;p1s, o为孔出口静压;A为孔进口面积。
孔的理论轴向速度计算公式为
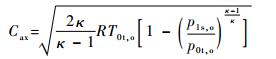
|
(3) |
当孔处于旋转状态时,采用式(2) 和式(3) 计算流量系数时,由于旋转盘面的泵效应,在低压比条件下可能出现Cd>1的情况[7],当孔所在半径高度的旋转速度为Ur时,为更好地分析旋转条件下的孔特性,Zimmermann等[6]提出了相对坐标系下的孔特性修正方法。

|
(4) |
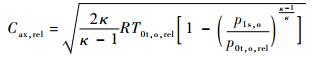
|
(5) |
式中:
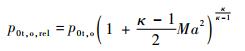
|
(6) |
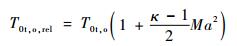
|
(7) |
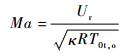
|
(8) |
当前对稳态条件下旋转孔流量系数的影响因素有大量的研究成果[7-11],对于旋转孔流量系数,在几何条件不变的情况下,主要的影响因素有进口雷诺数Re、压比π以及切向速度与轴向速度之比Ur/Cax,在相对坐标系下,取Ur/Cax, rel。其中,只有低雷诺数下,雷诺数变化对小孔流量的影响才会比较明显。Idris和Pullen[12]同时考虑了孔的旋转以及孔自身倾斜角的影响,采用进气攻角i作为孔流量系数的影响参数进行研究,定义为
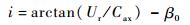
|
(9) |
式中:β0为孔的倾斜角。
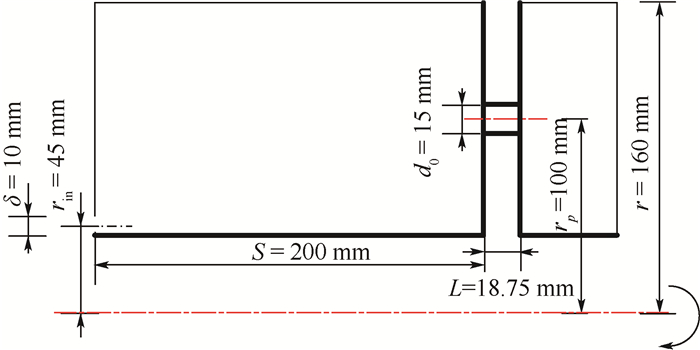
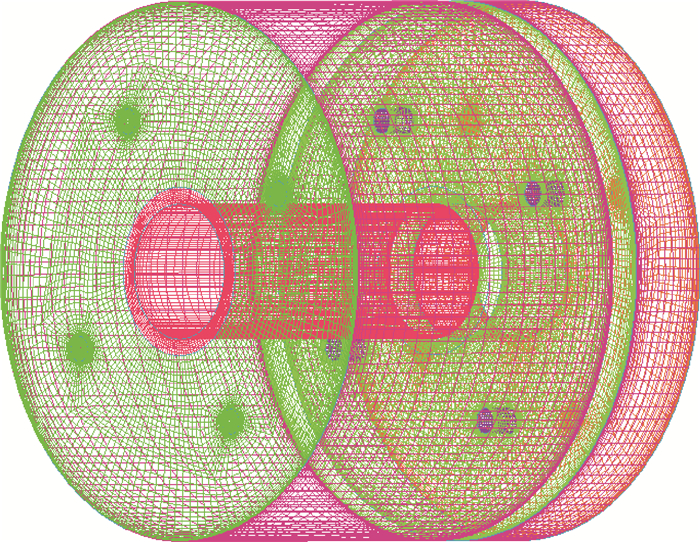
2 物理模型与计算工况在真实发动机几何中,旋转孔腔的结构往往比较复杂,本文的CFD计算模型采用了轴向孔结构,重点研究孔前腔的影响,并将前腔简化为圆柱形腔体,孔后为开放边界。旋转孔腔的几何结构与具体尺寸如图 1所示,粗线部分为旋转面,细线部分为静止面,流体从低半径处的环形进口流入腔体,经过旋转孔后流出。考虑到在瞬态过程中,腔内可能出现明显的非均匀现象,因此采用六面体网格对整环几何模型进行网格划分并求解,具体网格如图 2所示,模型中均匀分布4个小孔,长径比L/d0=1.25。
|
| 图 1 CFD计算模型几何结构示意图 Fig. 1 Schematic diagram of geometric structure of CFD model |
|
| 图 2 网格划分示意图 Fig. 2 Schematic diagram of mesh generation |
CFD计算采用ANSYS CFX进行,湍流模型选择CFX中的k-Omega模型,在该湍流模型下,计算可取得较好的收敛性,稳态计算残差基本可到10-5以下,部分稳态算例的残差在10-4以下。稳态计算设定计算总步长为2 000步,计算完成时,模型中的流量等计算参数基本不变。瞬态计算采用自适应步长方法求解,初始步长为10-7 s,自适应最大步长设为10-5 s,最小步长设为10-9 s,瞬态计算过程中,单步计算循环超过5次时,下一时间步长为前一步长的0.8倍,当单步计算循环低于2次时,下一时间步长为前一步长的1.06倍,瞬态计算的收敛残差为10-5。
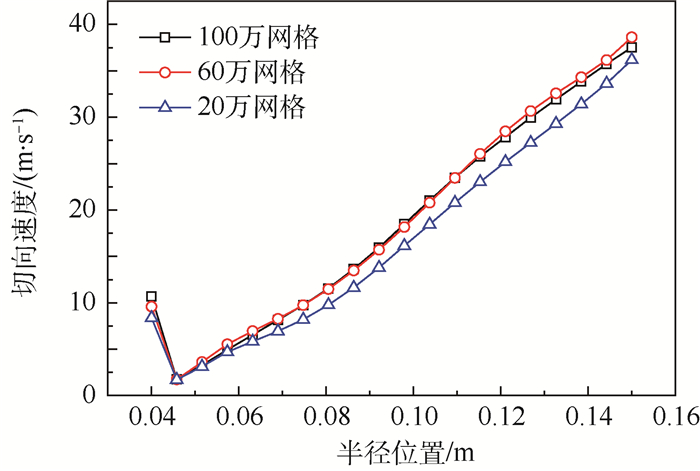
CFD计算模型采用六面体网格进行划分,并进行了网格无关性验证,验证过程中分别采用20万、60万、100万3个量级的网格进行对比,图 3给出了距离进口10 cm处一径向线上的切向速度随半径位置r的分布。可见,采用60万网格的结果与采用100万网格的结果比较接近,本文中的CFD计算最终所用网格为667 460。
|
| 图 3 网格无关性验证 Fig. 3 Grid independence verification |
网格划分过程中,对于壁面网格进行了加密处理,各壁面的第1层网格尺度均小于0.5 mm,其中孔与盘背面的第1层网格为0.05 mm。旋转孔壁面Y+各工况下最大约为100,最小Y+为5。其余壁面最大Y+根据工况不同约为150~250。
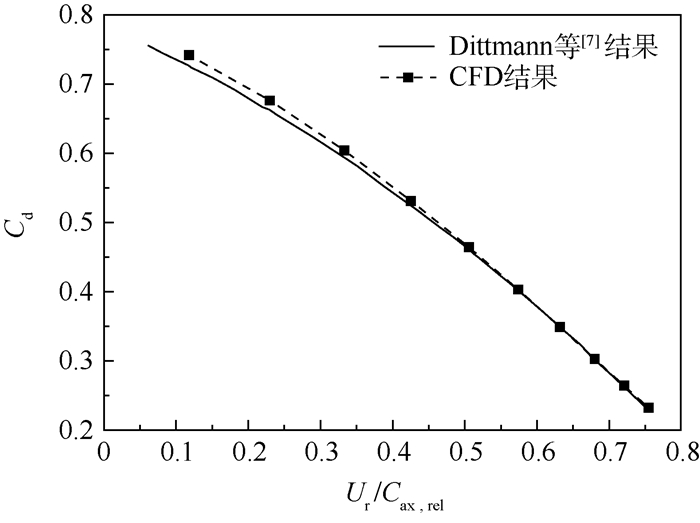
为保证计算的准确性,对该CFD计算模型进行了校验计算。校验计算时,进气总温为288.15 K,壁面条件为绝热无滑移,CFD进口总压p0t与出口静压p∞之比πm=1.05,获得不同转速下的小孔流量,采用式(4) 和式(5) 计算不同转速下的流量系数,式中所用的旋转孔进口总温与总压的选取位置与Dittmann等[7]试验一致。与Dittmann等[7]的试验结果对比如图 4所示,流量系数结果符合较好,最大误差不超过2%。
以该CFD计算模型为基础,进行了1组稳态数值模拟及2个瞬态过程的模拟。稳态工况的计算结果为瞬态1-D模型提供旋转孔流量系数拟合结果等稳态特性。稳态条件下,旋转孔的转速为10 000r/min,进气总温为288.15 K,壁面为绝热无滑移边界,调整CFD进口总压p0t与出口静压p∞之比πm从1.05到2.0变化,获得总计11组稳态计算结果,采用式(1) 和式(2) 计算稳态工况下的流量系数,其中孔进口总压采用绝对坐标系下的腔内平均总压pt, v,孔进口总温采用绝对坐标系下的腔内平均总温Tt, v,如式(10) 所示。Ao为孔的进口面积,腔内平均参数以脚标v表示,在CFD-post中采用体积平均获取腔内平均参数。
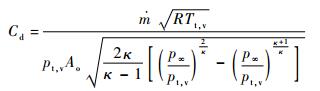
|
(10) |
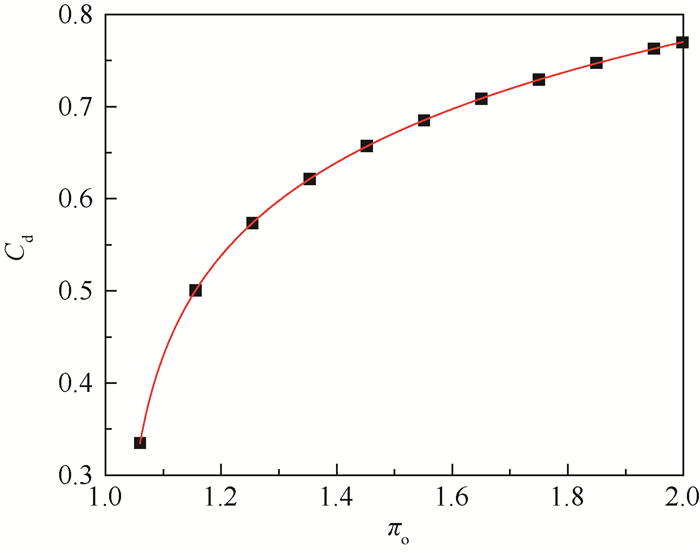
稳态工况计算过程中,转速和几何结构保持不变,因此可建立流量系数与孔前后压比(孔前绝对总压比孔后静压)πo的关系,稳态流量系数结果如图 5所示,曲线为拟合结果,其表达式为
|
| 图 5 稳态工况流量系数结果与拟合 Fig. 5 Discharge coefficient results and fitting under steady working condition |

|
(11) |
2个瞬态工况的计算过程中,旋转孔转速始终保持为10 000 r/min,控制进出口边界压比πm随时间变化,初始时刻,压比πm=1.05。
1) 斜坡工况,πm在0.02 s内由1.05线性上升至2.0后保持恒定。
2) 光滑工况,πm在0.02 s内上升至2.0后保持恒定,压比变化率呈梯形分布,其表达式见式(12)。
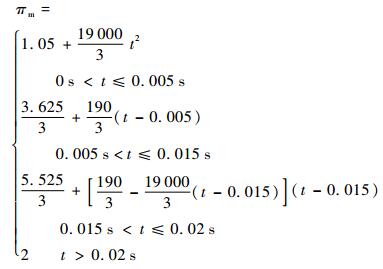
|
(12) |
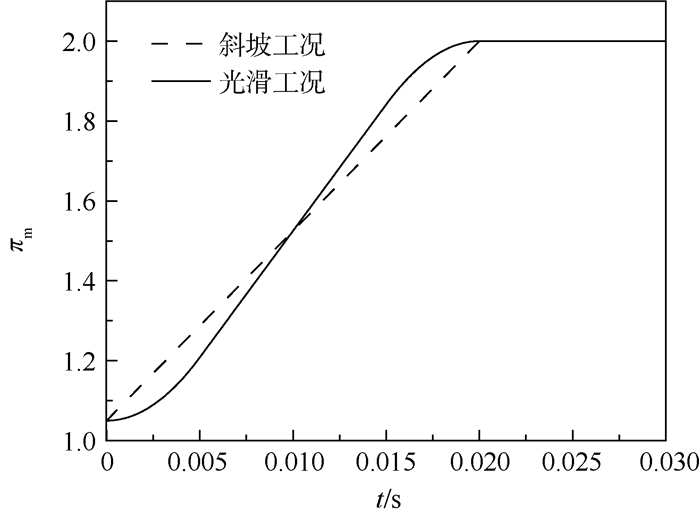
斜坡工况及光滑工况进出口压比变化如图 6所示。
|
| 图 6 瞬态工况压比随时间变化 Fig. 6 Change of pressure ratio with time under transient working condition |
瞬态1-D模型需要对孔前腔建立瞬态数学计算模型,Gallar等[4]为研究瞬态容腔的充放气过程,提出了瞬态容腔的数学建模方法。
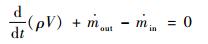
|
(13) |
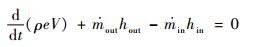
|
(14) |
式中:e为比内能;h为比焓;ρ为密度;V为体积。
式(14) 和式(15) 成立的条件为容腔中无额外热量进出,忽略浮升力以及流动速度。通过以上假设,Gallar等[4]把容腔视为内部各处均匀的节点,以集总的方式建立容腔的低维模型。
假设比热容在瞬态过程中保持恒定,腔室体积恒定且考虑旋转盘扭矩做功的影响,式(13) 与式(14) 可化为
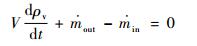
|
(15) |
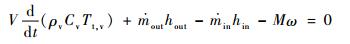
|
(16) |
式中:M为扭矩;Cv为定容比热;ω为盘旋转角速度。
采用Euler隐式格式进行离散可得
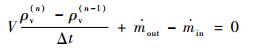
|
(17) |

|
(18) |
式中:Cp为定压比热。
腔内气体的平均密度由理想气体状态方程导出:

|
(19) |
从稳态CFD结果中可获取孔腔内盘面与旋转轴的扭矩,在对扭矩进行分析中往往将扭矩无量纲化,获得扭矩系数Cm[13],其定义为
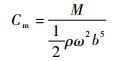
|
(20) |
式中:密度ρ取腔内平均密度;b取旋转盘半径。通过对稳态结果的计算,发现整体上扭矩系数变化不大,为0.003 3~0.003 5,简化考虑,在瞬态1-D模型中取固定扭矩系数Cm=0.003 4。
进口流量与出口流量的计算式为式(21) 和式(22),其中出口流量计算中的孔流量系数采用式(11) 中稳态CFD计算的拟合结果。
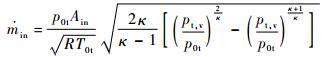
|
(21) |
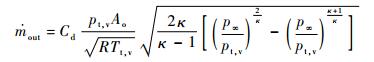
|
(22) |
低维模型的计算时间步长为0.000 1 s,求解过程中,采用本时刻的进口压力和上一时刻的计算结果作为初场,采用离散牛顿法对非线性方程组进行迭代求解,直至残差小于10-6,完成本时刻结果的计算,进入下一时刻的计算。
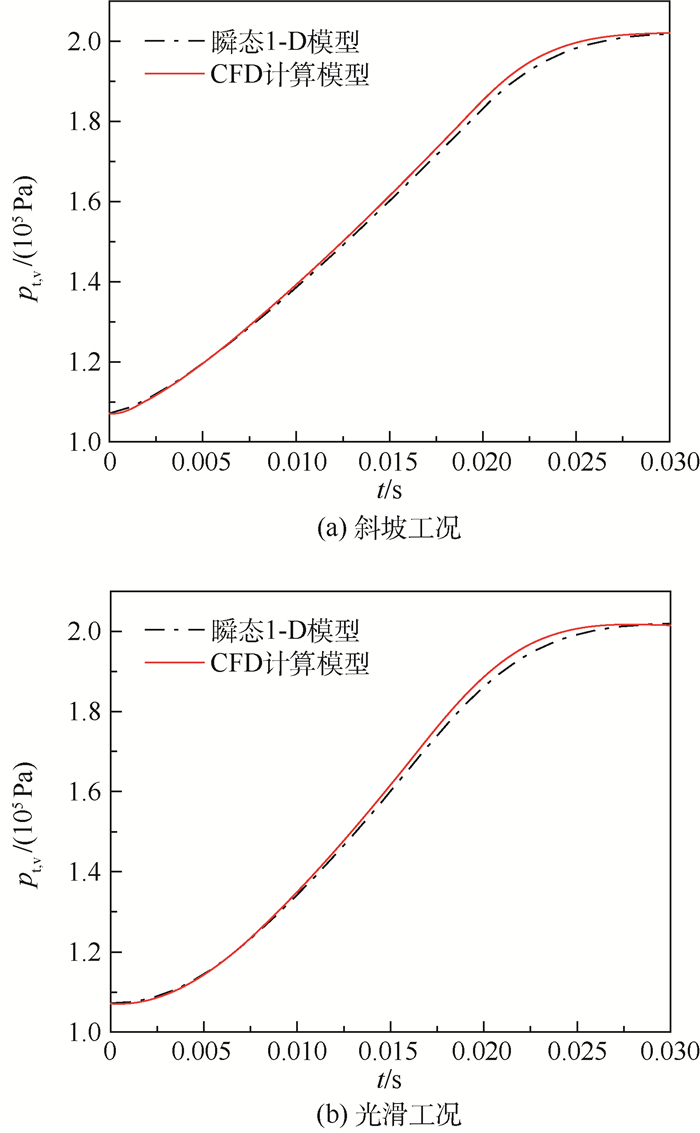
4 瞬态1-D模型与CFD计算模型结果对比 4.1 腔内平均总压图 7为孔腔内平均总压的对比结果。采用瞬态1-D模型能够较好地获得腔内平均总压随时间的变化规律,斜坡工况腔内压力最大误差为1.7%,光滑工况腔内压力最大误差与斜坡工况相当。说明在较强的瞬态过程下,瞬态1-D模型对于腔内平均总压的变化有较好的模拟。
|
| 图 7 瞬态工况腔内平均总压结果 Fig. 7 Average total pressure results in cavity under transient working condition |
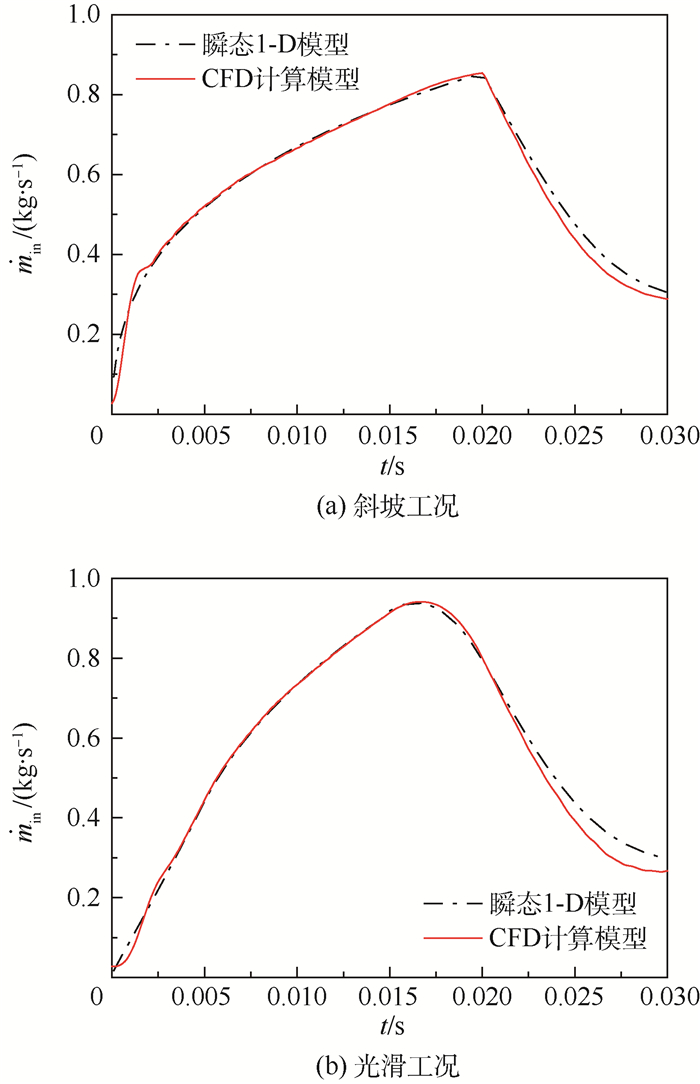
图 8为进口流量的结果对比。可见,在瞬态过程中,瞬态1-D模型的进口流量结果随时间的变化趋势仍能保持与CFD结果相同,能够较好地反映进口流量随时间的变化规律,但是部分时间段存在一定的误差。从斜坡工况结果来看,由于进口压力变化比较剧烈,所以在0.001 s处形成了明显的振荡,瞬态1-D模型无法捕捉这一振荡现象。此外,0.02 s后,进口流量的误差先增后减,最大可达9%左右。而对于光滑工况,初始时段进口压力缓慢上升,使初始段的振荡得到了抑制,但进口压力稳定后出口流量的误差最大会达到19%。
|
| 图 8 瞬态工况进口流量结果 Fig. 8 Inlet flow rate results under transient working condition |
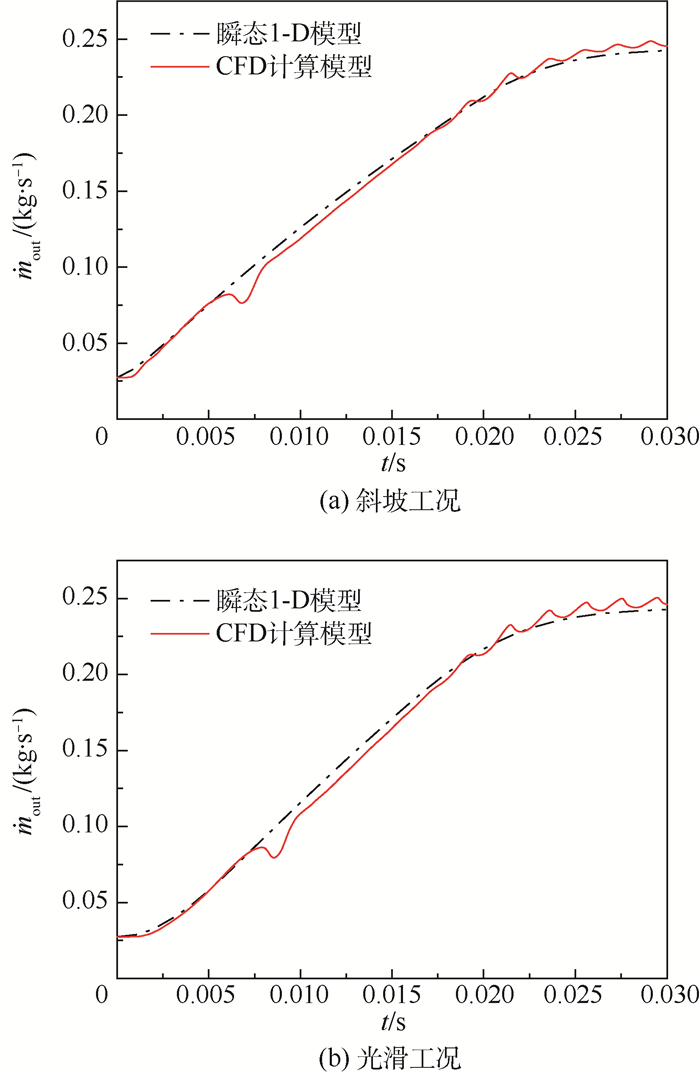
瞬态过程中,如图 9所示,出口流量整体趋势上与CFD结果基本吻合,但是CFD计算过程中,出口流量并没有单纯随腔内平均总压的增加而增加,在0.007 s时,斜坡工况和光滑工况的出口流量先后出现了明显的下降,而瞬态1-D模型计算得到的出口流量始终随着腔内平均总压在平稳增长,在压力趋稳阶段,CFD的出口流量结果出现规律振荡,即使腔内平均总压趋于稳定,该振荡依然存在并处于缓慢消减的状态。从误差来看,出口流量突降处,瞬态1-D模型与CFD结果最大误差能达到21%,而进口压力稳定后的振荡段,最大误差约为3%。另外在0.01~0.017 s时间段内,瞬态1-D模型对光滑工况出口流量的计算结果误差要略高于斜坡工况。
|
| 图 9 瞬态工况出口流量结果 Fig. 9 Outlet flow rate results under transient working condition |
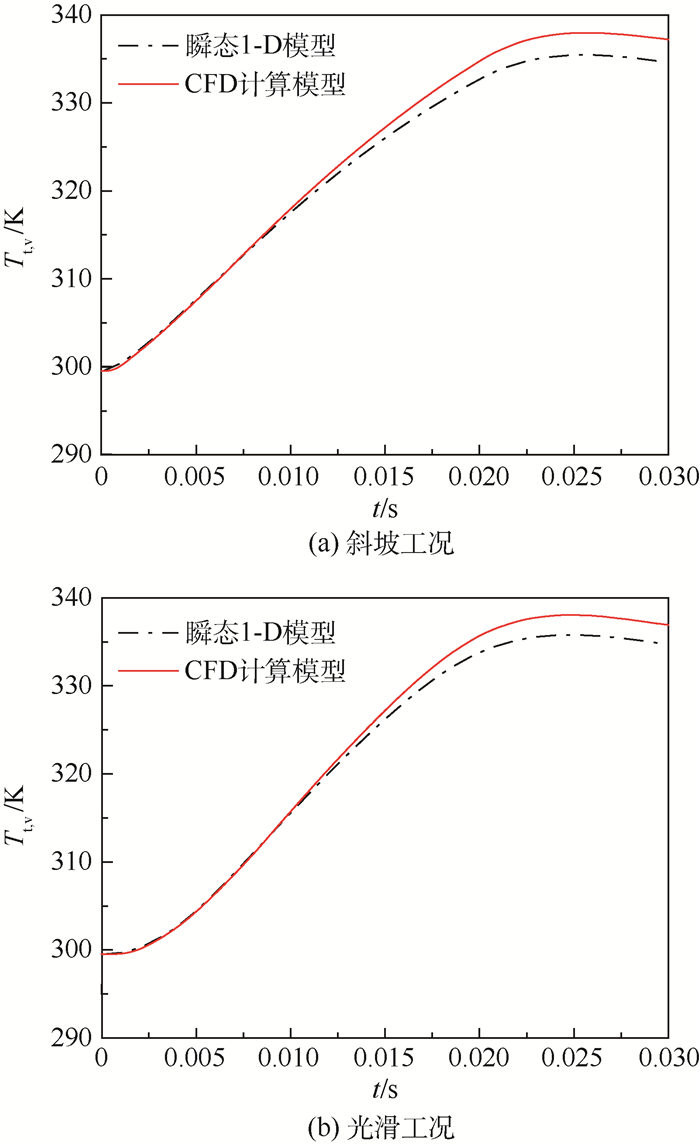
从图 10可以看出,瞬态1-D模型低估了腔内的平均总温,随着时间的推进,模型结果与CFD结果差距逐渐增加。尽管在整体温度的变化趋势上,瞬态1-D模型与CFD结果相吻合,但相对于0.03 s内的总温变化量,瞬态1-D模型最大误差约为8%。
|
| 图 10 瞬态工况腔内平均总温结果 Fig. 10 Average total temperature results in cavity under transient working condition |
瞬态1-D模型是基于腔内参数均匀的假设,采用集总的方式建立,而孔特性直接采用了稳态条件下计算得到的流量系数特性曲线。分析瞬态1-D模型的误差,主要有以下2方面:
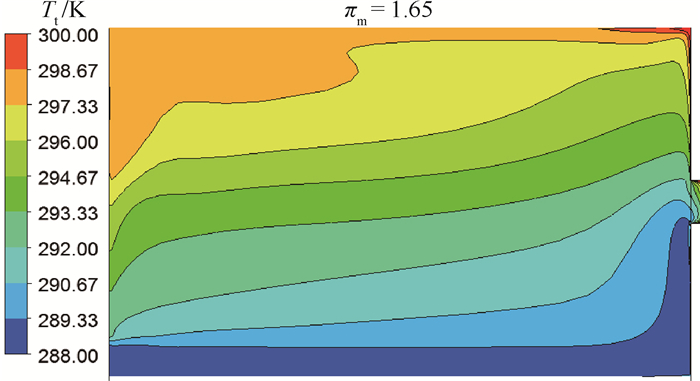
1) 稳态工况下自身的非均匀性造成的误差。图 11为模型进出口边界压比为1.65条件下,CFD计算得到的腔内总温的分布云图。可见,高半径处的总温明显高于低半径处,实际条件下,进入孔的流体总温略低于腔内平均总温。瞬态1-D模型假设稳态条件下腔室为各项参数均匀的节点,忽略了腔内温度的分布特性,采用该假设已经引入了一定的误差。
|
| 图 11 稳态工况下腔内总温分布云图 Fig. 11 Distribution contour of total temperature in cavity under steady working condition |
2) 瞬态过程偏离稳态结果的误差。瞬态1-D模型的旋转孔特性来源于稳态计算结果,但是实际的瞬态过程中,由于内部流动与稳态有非常明显的差异,可能使得直接采用稳态条件下的特性曲线无法准确计算当前的瞬态过程,从而导致瞬态1-D模型预测失准。
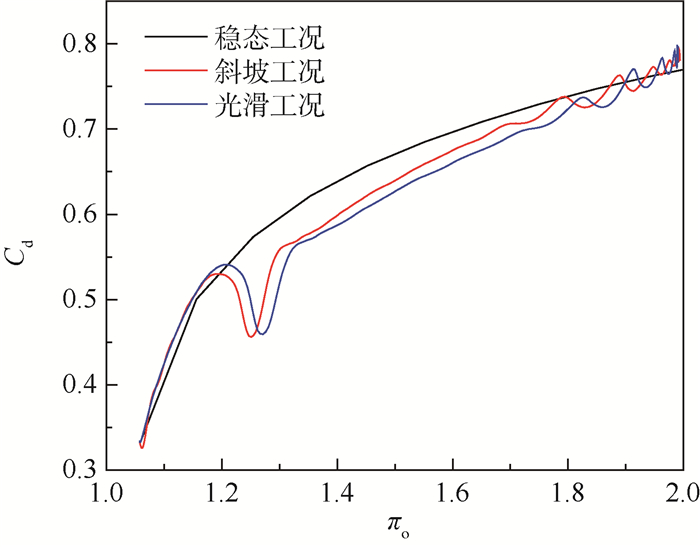
5.1 流量结果误差分析从CFD计算模型与瞬态1-D模型的对比结果可以看出,虽然流动过程与稳态已经有了一定的区别,但瞬态1-D模型仍能较好地反映流量的整体变化规律,只是在部分时间段误差比较大,尤其是CFD的出口流量结果,出现了流量随压力减小的现象。从图 12流量系数的对比结果可以发现,瞬态条件下,不仅出现了流量系数的不合理下降,同时整体也与稳态结果有一定的偏离。瞬态1-D模型采用了稳态结果的流量系数,所以在模拟瞬态过程时符合稍差。
|
| 图 12 瞬态与稳态工况下流量系数对比 Fig. 12 Comparison of discharge coefficient under transient and steady working conditions |
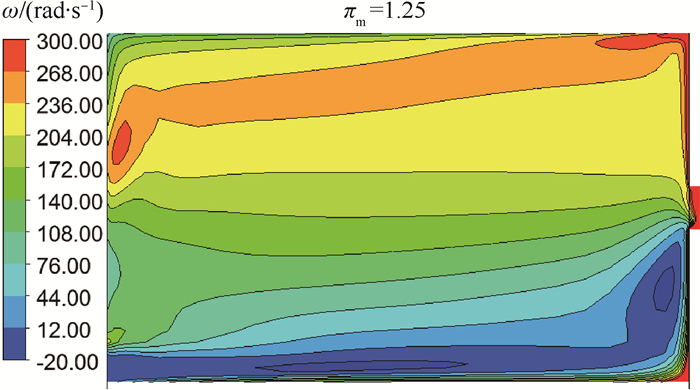
在几何固定且进口雷诺数较大的条件下,流量系数主要受压比和转速的影响,而转速的影响主要来源于孔前流体进入孔时的攻角[11]。瞬态过程中,孔腔内的平均总压以及旋转孔进口处的总压均没有出现突降现象,因此流量突降可能是由于孔前流体自身的切向速度变化引起进气攻角改变而造成的。在小孔稳态流量特性的研究中,一般认为旋转引起的来流切向速度很小[14]。而罗翔等[15]研究旋转盘腔时发现,当通流较小时,腔内的流场是受到旋转主导的,流体的旋转速度会比较快,而当通流较大时,强烈的惯性作用会抑制转盘对流体的加速。图 13为稳态工况下,CFD计算结果中进出口边界压比为1.25时,孔腔内的角速度云图。可以看出,孔前流体的角速度呈现半径越高角速度越高的分布趋势,来流以一定的切向速度跟随旋转孔转,可以减小进气攻角,增大流量。除旋转速度以外,还需考虑径向速度的影响,因为该模型进气半径位置低于旋转孔,因此进口气流需沿径向往高半径位置流动才能进入旋转孔流出,这一径向速度的改变也可能影响孔的流量系数。
|
| 图 13 稳态工况下腔内角速度云图 Fig. 13 Contour of angular velocity in cavity under steady working condition |
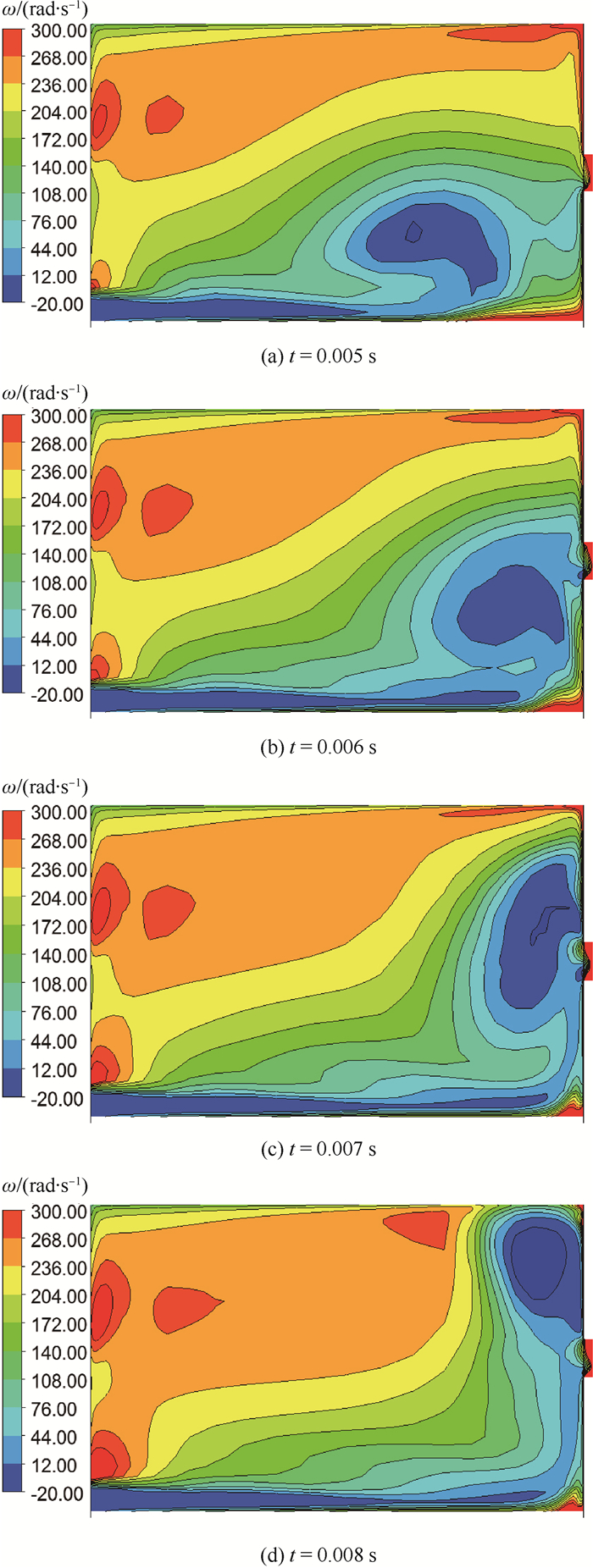
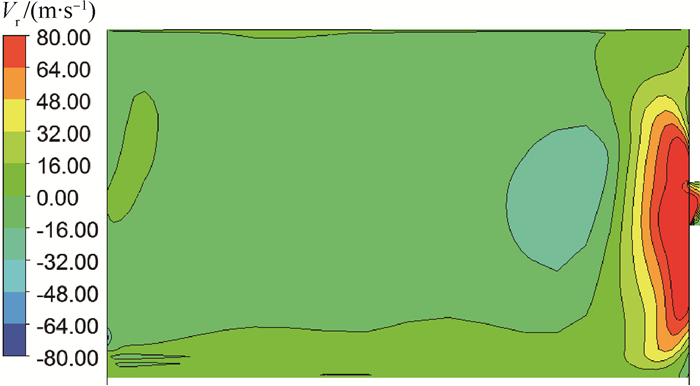
在瞬态过程中,进口压力迅速上升,使得一团角速度极小的气体被推向了孔的进口处,导致孔前角速度减小,径向速度增大,整个旋转孔的进气攻角增加。图 14为斜坡工况条件下孔腔内的角速度云图,在0.006~0.008 s之间,图中角速度极小的深蓝色气团封堵了旋转孔口。从图 15的径向速度Vr云图可见,该气团也使得孔前出现较大的径向流动,此时孔前切向流动较强,进气攻角增大明显。该气团封堵旋转孔的时间与孔流量突降相吻合,因此可推断,孔前出现较强切向流动增大了进气攻角,是造成流量系数下降的主因。此后,孔前始终受到切向流动的影响使得瞬态1-D模型计算的出口流量一直高于CFD计算的出口流量,最终影响瞬态1-D模型中对腔内压力和进口流量的计算结果。
|
| 图 14 斜坡工况下腔内角速度演化过程 Fig. 14 Evolvement of angular velocity in cavity under slope working condition |
|
| 图 15 斜坡工况下0.007 s时刻腔内径向速度云图 Fig. 15 Contour of radial velocity in cavity at 0.007 s under slope working condition |
对于0.02 s后出口流量的振荡现象,可以通过孔前流体的角速度分布进行分析。如图 16所示,当腔内平均总压逐渐趋于稳定后,压比对流量系数的影响减小,而孔腔内的流动尚未达到稳定状态,这段时间内,孔前流体的角速度不断变化,因此导致了孔流量出现了明显的振荡。

|
| 图 16 斜坡工况下孔前截面角速度演化 Fig. 16 Evolvement of angular velocity in cross section in front of orifice under slope working condition |
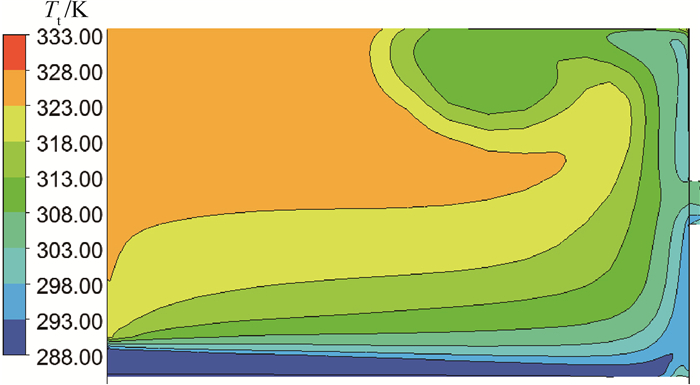
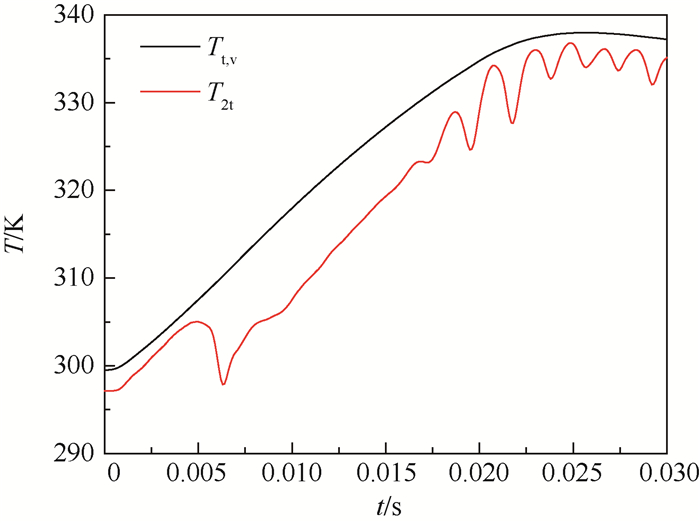
从CFD计算结果可以发现,在瞬态过程中,进口流量较大。图 17为0.01 s时斜坡工况下腔内的总温分布云图。可以看出,瞬态过程中,进口流量迅速增加,进口处涌入的大量气体从低半径处冲击旋转盘后封堵了旋转孔,将高半径处温度较高的气体推离旋转孔,使得旋转孔的进口总温相对于稳态条件下降明显。图 18为斜坡工况计算过程中,腔内平均总温与旋转孔进口总温随时间的变化。可见,孔进口总温明显低于腔内平均总温。绝对坐标系下,孔进口总温与腔内平均总温之比T2t/Tt, v最低能达到0.93以下。因此,瞬态1-D模型过高地估计了出口焓,最终导致瞬态1-D模型中计算得到的腔内总温相对于CFD结果偏低。
|
| 图 17 斜坡工况下腔内总温分布云图 Fig. 17 Distribution contour of total temperature in cavity under slope working condition |
|
| 图 18 斜坡工况下腔内总温与孔进口总温对比 Fig. 18 Comparison of total temperature between cavity and inlet of orifice under slope working condition |
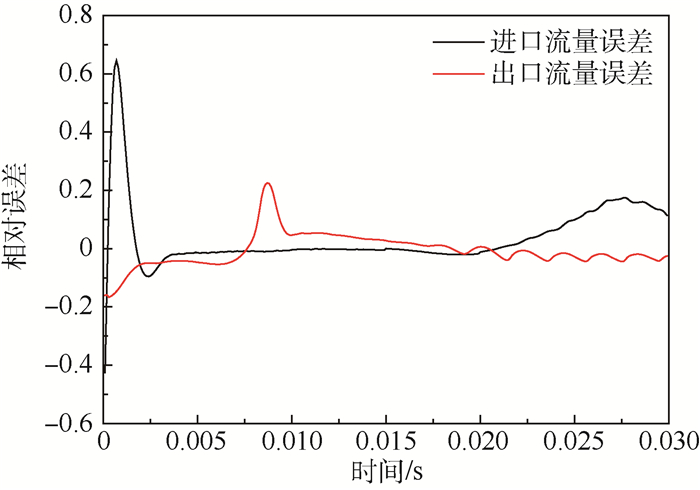
从结果分析可以看出,虽然瞬态1-D模型整体上已经符合较好,但是无法做到与CFD结果完全相同,在部分时间内误差较大,而部分时间误差较小。图 19为光滑工况条件下进出口流量误差随时间变化的结果。可以看出,在瞬态计算过程中,既有可能出现持续时间较长的误差,也可能出现短时的较大误差。
|
| 图 19 光滑工况下进出口流量误差变化 Fig. 19 Variation of inlet and outlet flow rate errors under smooth working condition |
稳态条件下,可以根据工程需要,确定流体网络法设计计算时的精度要求,定义模型与真实结果的相对误差为
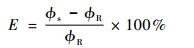
|
(23) |
式中:E为相对误差;ϕs为模型结果;ϕR为实际结果。
在瞬态条件下,不同时刻的相对误差不同,因此有

|
(24) |
瞬态低维模型的计算目的不同,对这些短时的较大误差的敏感度也不尽相同。比如气膜冷却的瞬态研究中,短时间的冷气流量偏低就可能导致叶片烧蚀,而对涡轮盘强度寿命的影响,短时间的冷气变化影响可能不明显。因此对于瞬态过程,不管采用瞬态过程中的最大误差,还是最小误差,或全过程的平均误差,都难以对模型的结果做出合理评价。在瞬态模型的误差分析中,不能忽略时间尺度的影响。
如果以Δτ作为误差分析的时间尺度,通过对Δτ内的平均参数建立瞬态过程的误差,有
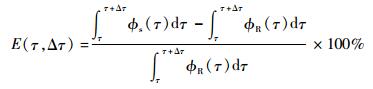
|
(25) |
当待分析结果对短时误差敏感时,Δτ取较小值;反之,Δτ取较大值。可定义瞬态误差分析的时间分辨率为1/Δτ,即对瞬态过程越敏感,分析误差时采用的分辨率越大。
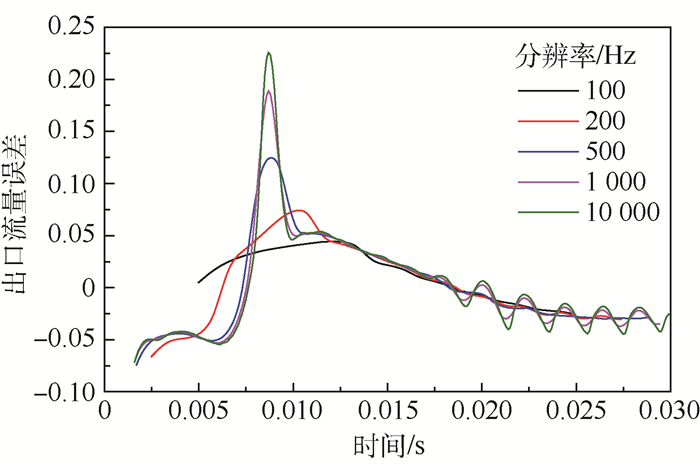
图 20为不同分辨率时光滑工况时出口流量误差的结果。不同分辨率下,误差结果有较为明显的差异。在100Hz和200Hz的分辨率下,出口流量的误差始终小于10%,随着分辨率的提高,CFD计算时的流量突降所带来的误差影响越明显,对于光滑工况的出口流量结果,满足10%@200 Hz的精度要求,却不满足10%@500 Hz的精度要求。根据不同的计算目的,合理选择精度要求与分辨率需求,方能对瞬态1-D模型的计算结果做出合理的工程评价。
|
| 图 20 不同分辨率下光滑工况的出口流量误差 Fig. 20 Outlet flow rate errors under smooth working condition with different resolution |
1) 以稳态孔特性为基础,考虑容腔在瞬态过程中的容积效应,建立瞬态1-D模型,对于较强的瞬态过程,能够从整体上反映流量和压力的演化。瞬态过程中,进口流量快速上升和快速下降的过程都能较好的模拟。
2) 较强瞬态过程中,细节的流动过程无法通过瞬态1-D模型进行模拟,采用集总方式建立的瞬态1-D模型无法在瞬态过程中为旋转孔提供准确的进气边界条件,可能使模拟结果出现较大的误差,因此需要对瞬态过程的流动细节加以更充分的研究,从机理层面对瞬态1-D模型进行修正。
3) 腔内温度有较强的不均匀性,且出口焓比较明显地受到温度分布和进口流量的影响,而当前瞬态1-D模型均匀性的假设,导致瞬态1-D模型得到的温度结果有明显偏差。目前认为,进口流量对旋转孔进口总温有明显影响,因此进一步的温度修正中,应当将进口流量的影响加以考虑。
4) 低维瞬态模型的精度要求,不考虑误差随时间的动态变化是不合理的,本文提出了带时间分辨率的误差分析思路,将低维瞬态模型的误差分析限定在满足工程需要的时间分辨率下,可用于研究瞬态低维模型的适用性。
| [1] | PRICE B, DEMERS L, LEBEL J F, et al.Enhancements to the load acceptance and rejection capability of a high pressure aeroderivative engine[C]//Proceedings of the 2007 ASME Turbo Expo.New York:ASME, 2007, 2:1051-1060. |
| [2] |
刘传凯, 刘海明, 李艳茹, 等. 强瞬变空气系统的模块化仿真建模[J].
航空动力学报, 2015, 30 (8): 1826–1833.
LIU C K, LIU H M, LI Y R, et al. Modularized simulation of air system with fast transients[J]. Journal of Aerospace Power, 2015, 30 (8): 1826–1833. (in Chinese) |
| [3] | CALCAGNI C, GALLAR L, PACHIDIS V.Development of a one dimensional dynamic gas turbine secondary air system model-Part Ⅱ:Assembly and validation of a complete network[C]//Proceedings of the 2009 ASME Turbo Expo.New York:ASME, 2009, 4:435-443. |
| [4] | GALLAR L, CALCAGNI C, PACHIDIS V, et al.Development of a one dimensional dynamic gas turbine secondary air system model-Part Ⅰ:Tool components development and validation[C]//Proceedings of the 2009 ASME Turbo Expo.New York:ASME, 2009, 4:457-465. |
| [5] |
李澎, 吴宏, 陶智. 二次空气系统一维非定常计算方法[J].
航空动力学报, 2014, 29 (7): 1710–1720.
LI P, WU H, TAO Z. One-dimensional unsteady calculational method of secondary air system[J]. Journal of Aerospace Power, 2014, 29 (7): 1710–1720. (in Chinese) |
| [6] | ZIMMERMANN H, KUTZ J, FISCHER R.Air system correlations.Part 2:Rotating holes and two phase flow[C]//Proceedings of the 1998 International Gas Turbine & Aeroengine Congress & Exhibition.New York:ASME, 1998:V004T09A049. |
| [7] | DITTMANN M, DULLENKOPF K, WITTIG S.Discharge coefficients of rotating short orifices with radiused and chamfered inlets[C]//Proceedings of the 2003 ASME Turbo Expo.New York:ASME, 2003:1001-1009. |
| [8] | ROHDE J E, RICHARDS H T, METGER G W.Discharge coefficients for thick plate orifices with approach flow perpendicular and inclined to the orifice axis:NASA-TN-D-5467[R].Washington, D.C.:NASA, 1969. |
| [9] | MEYFARTH P F, SHINE A J. Experimental study of flow through moving orifices[J]. Journal of Basic Engineering, 1965, 87 (4): 1082–1083. DOI:10.1115/1.3650814 |
| [10] | WITTIG S, KIM S, JAKOBY R, et al.Experimental and numerical study of orifice discharge coefficients in high speed rotating disks[C]//Proceedings of the International Gas Turbine and Aeroengine Congress and Exposition.New York:ASME, 1994:V001T01A052. |
| [11] | IDRIS A, PULLEN K R, READ R.The influence of incidence angle on the discharge coefficient for rotating radial orifices[C]//Proceedings of the 2004 ASME Turbo Expo.New York:ASME, 2004, 4:307-320. |
| [12] | IDRIS A, PULLEN K R. Correlations for the discharge coefficient of rotating orifices based on the incidence angle[J]. Proceedings of the Institution of Mechanical Engineers Part A-Journal of Power and Energy, 2005, 219 (5): 333–352. DOI:10.1243/095765005X31153 |
| [13] | BAYLEY F J, OWEN J M. Flow between a rotating and stationary disc[J]. Aeron Quart, 1969, 20 (4): 333–354. DOI:10.1017/S000192590000514X |
| [14] | SOUOSEK J, PFITZNER M, NIEHUIS R.Experimental study of discharge coefficients of radial orifices in high-speed rotating shafts[C]//Proceedings of the 2010 ASME Turbo Expo.New York:ASME, 2010, 4:1051-1060. |
| [15] |
罗翔, 张达, 徐国强. 中心进气开式转静系转盘风阻扭矩实验[J].
推进技术, 2015, 36 (8): 1199–1205.
LUO X, ZHANG D, XU G Q. Experimental study on windage torque in unshrouded rotor-stator system with central inflow[J]. Journal of Propulsion Technology, 2015, 36 (8): 1199–1205. (in Chinese) |