2. 91934 部队, 义乌 322000
2. 91934 Army, Yiwu 322000, China
作为一种时间序列,不等长序列数据的关联是异类传感器融合必须解决的问题,其根本方法是对不等长度序列数据相似度的挖掘和度量,特别是干扰条件下量测序列出现突变点的情况。文献[1-15]相继研究了时间序列相似度的查询,形成了一系列序列度量的方法,离散傅里叶变换[1-3]、奇异值分解[4]、离散小波变换[5-6]、分段合计近似[7-8]、动态时间弯曲(DTW)[8-13]、分段线性表示[8, 14]、分段多项式表示[15]等。这些方法从不同的角度对不等长序列进行度量,在各自的变换域内取得了较好的效果,但就单个模型而言,随着序列长度变化在计算精度、复杂度和抗扰性上不能兼容,比如Keogh等[8]阐述了DTW的计算高精度,但是时间复杂度上存在较大的冗余。为了兼顾不等长序列相似度度量的计算精度、复杂度和抗扰性,提出了一种基于多模型(MM)的不等长序列数据度量算法,采用基于滑动窗口的不等长序列度量模型和基于DTW的不等长突变序列度量模型作为MM的输入模型,定义了时似变化比作为模型转换指标,根据时似变化比调节模型进行转换,给出了序列长度变化时的2种模型共同作用的输出结果,既保证了滑动窗口模型的快速计算,又稳定了DTW突变模型的高精度和抗扰性。最后将MM共同作用输出的不等长序列相似度作为数据关联的指标,采用最大相似度准则进行关联判决。
1 基本概念 1.1 不等长序列的表示记长度为n的序列表示为
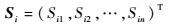
|
(1) |
式中:Sij为序列i的第j个数据值,记序列的长度为|Si|,则|Si|=n,如果|Si|≠|Sj|,则称序列Si和序列Sj为不等长序列。
由m条序列数据组成的不等长序列数组表示为
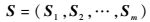
|
(2) |
记序列Si=(Si1, Si2, …, Sin)和Qi=(Qi1, Qi2, …, Qin)之间的相似度为
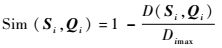
|
(3) |
式中:D(Si, Qi)为序列Si和Qi之间的距离度量,其定义为
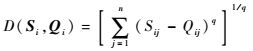
|
(4) |
计算过程中一般选取q=2,即Euclidean距离进行计算。Dimax为距离度量的最大值:

|
(5) |
若不等长序列数组的属性权向量:
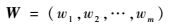
|
(6) |
则不等长序列数组S=(S1, S2, …, Sm)和Q=(Q1, Q2, …, Qm)的综合相似度为
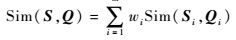
|
(7) |
干扰条件下传感器的某个或某些量测数据偏离实际数据而出现的一些抖动剧烈的点迹称为突变点,如图 1所示。
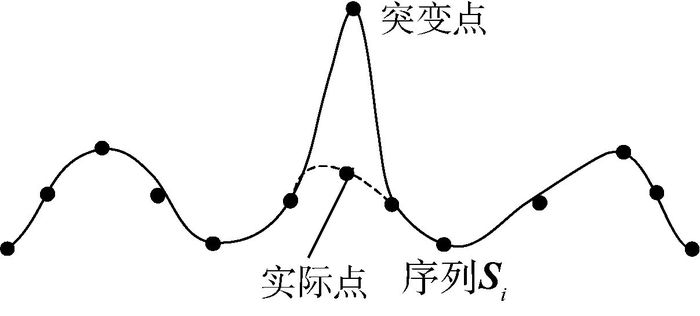
|
| 图 1 突变点示意图 Fig. 1 Schematic diagram of fluctuant point |
定义1 突变率r为
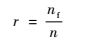
|
(8) |
式中:序列中nf为突变点的个数。
2 不等长序列相似度度量模型 2.1 滑动窗口的不等长序列基于滑动窗口的不等长序列相似度度量指的是,将参考序列和比较序列中长度较短的序列作为滑动窗口,沿较长序列依次遍历一个单位,遍历过程中计算窗口内对应的等长序列的滑窗相似度,直至较长序列所有点遍历完毕。最后将遍历过程中得到的滑窗相似度进行组合,作为2条不等长序列的相似度,组合过程中,为了突出匹配效果,采用了一种基于滑窗相似度的最优匹配增权策略。
假设2条属性关系对应的不等长序列Si和Qi,令
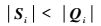
|
(9) |
以序列Si作为窗口沿序列Qi依次滑动一个单位,并根据式(3)~式(5) 计算滑动过程中的滑动相似度Simei(Si, Qj),则滑动结束后可以得到一组滑动相似度向量:

|
(10) |
得到滑动相似度之后,基于滑动相似度按照最优增权策略加权组合滑动相似度就可以得到2条不等长序列Si和Qi之间的相似度,首先进行权重的确定。
由于窗口滑动过程中,计算的序列滑动相似度根据窗口内序列数据的不同是不断变化的,所以在加权组合滑动相似度时需要进行权重有效的分配,以突出滑动相似度所对应序列的匹配程度,即所谓的最优匹配增权策略。
所以根据滑动相似度的大小将权向量定义为
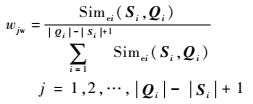
|
(11) |
则按照最优匹配增权策略加权组合滑动相似度Simei(Si, Qi)得到不等长序列Si和Qi之间的相似度为
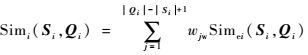
|
(12) |
基于DTW的不等长突变序列相似度度量指的是,当序列中存在突变点数据时,首先基于DTW计算2条不等长序列之间的绝对距离矩阵,并对绝对距离矩阵按行或列提取最小距离形成最小绝对距离集合,之后为了减弱突变点对序列距离的影响,采用平权1-范数度量最小绝对距离集合中的元素作为序列的距离,又考虑到最小绝对距离集合中的每行或列中的最小值可能不唯一,直接求和会造成重复弯曲的问题,导致距离变大,所以对平权1-范数度量进行加权因子修正处理,将修正后的距离作为序列的距离度量,最后根据距离与相似度度量的转换关系,计算得到不等长突变序列的相似度。
构造不等长序列Si与Qi的绝对距离矩阵Mi,即将序列Si与Qi中的元素沿矩阵横向和纵向展开,计算2条序列中任意2个元素的绝对值形成:
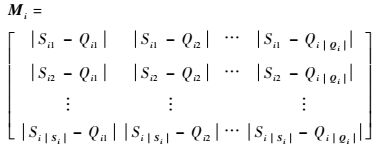
|
(13) |
假设|Si|<Qi,则令
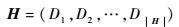
|
(14) |
式中:H为按Si中元素遍历Qi中所有元素形成的最小绝对距离集合,|Si|≤|H|≤|Si|·|Qi|;最小绝对距离为

|
(15) |
用语言表述H即为绝对距离中每列元素中的最小值组成;若|Si|>Qi则为行元素最小值构成。
由于图 1所示的突变点的存在,使得最小绝对距离集合中的某些元素偏离实际值,产生较大距离,为了减弱突变点的影响,采用平权1-范数对最小绝对距离集合进行度量,这样就将突变点的影响平均化,减小了其对不等长序列度量造成的误差。不等长序列Si和Qi的平权1-范数距离度量为
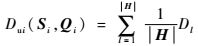
|
(16) |
又考虑到最小绝对距离集合H中可能会有多个相同最小值,如果直接按照平权1-范数累加组合,必然会造成重复弯曲的问题,即将原本不该累加的元素进行了求和,使得距离度量变大。考虑到上述问题,对表示不等长序列Si和Qi之间的距离的平权1-范数Dui(Si, Qi)进行修正为
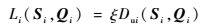
|
(17) |
式中:ξ为修正因子,修正因最小值重复造成的重复弯曲问题,ξ可以定义为
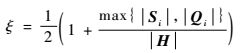
|
(18) |
则不等长序列Si与Qi的距离度量写成DTW规范形式为
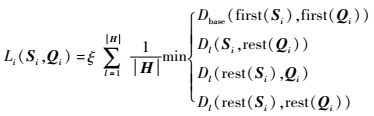
|
(19) |
式中:Dbase为任意一种距离计算;first()为不等长序列长度相同部分对应的序列;rest()为不等长序列长度不等部分对应的序列。
根据式(3)~式(5) 距离和相似度度量的转化关系,得到不等长序列Si和Qi的相似度度量:
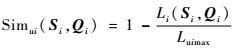
|
(20) |
式中:Luimax=max{Li(Si, Qi), i=1, 2, …, |H|}。
3 模型的转换及关联判定 3.1 模型的转换多模型算法[16]是自动控制领域常用的一种算法,它由多个滤波器(对应相应的模型)、一个模型概率计算器、一个估计混合器组成,考虑多个模型的共同作用,来得出目标的估计。
定义2 归一化的时间变化率与相似度变化率的比值称为时似变化比,其可表示为
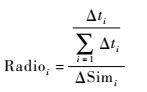
|
(21) |
式中:Δti和ΔSimi分别为模型计算的时间变化率与相似度变化率。
在序列度量领域,随着序列长度的增加,基于DTW的不等长突变序列相似度度量由于其计算的复杂性会出现时间上的高冗余,而随着突变点的增加,基于滑动窗口的不等长序列相似度度量由于其抗扰性差,得到的相似度度量误差较大,所以为了兼顾滑动窗口模型的快速计算性和DTW模型的高精度和抗扰性,本文基于MM的思想,将上述2种模型作为MM的作用模型,考虑2个模型的共同作用,将时似变化比作为模型切换的指标,在突变点存在的不等长序列相似度度量条件下,当序列长度较小时,2种模型的时间变化较小,而相比滑动窗口模型,DTW模型由于处理突变点的优越性,相似度增加很快,所以序列长度较小时DTW模型的时似变化比要比滑动窗口模型小。而随着序列长度增加,DTW模型的时间变化急剧增加,而滑动窗口模型时间增加缓慢,且突变率减小,相似度增加变快,所以在序列长度增加过程中滑动窗口模型的时似变化比要比DTW模型小。
当输入某个长度的不等长序列时,利用2种模型分别进行计算输出时似变化比,将时似变化比作为模型转换的指标,组合输出不等长序列的相似度度量。模型工作流程图如图 2所示。
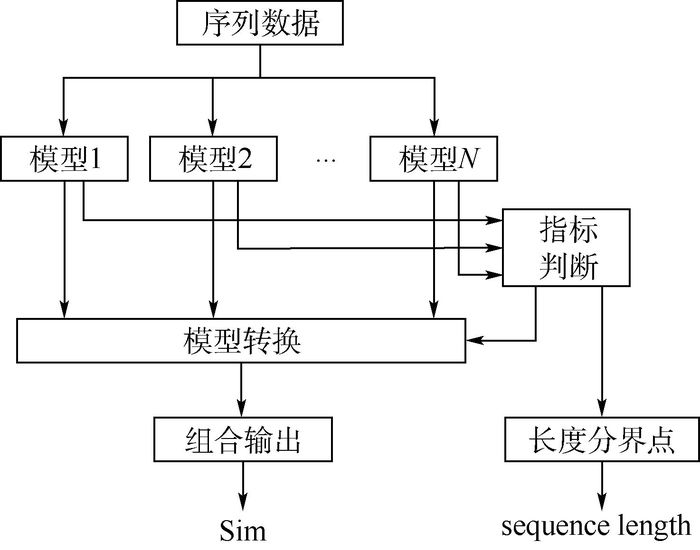
|
| 图 2 模型转换流程图 Fig. 2 Model transformation flowchart |
通过上述分析,将时似变化比指标较小的模型作为交互的主要模型进行交互作用,能够同时满足2种模型的共同优点,则指标判断可以表示为
If Radioi1<Radioi2
go model 1
else if Radioi1=Radioi2
output sequence length
else
go model 2
End
则多模型共同作用得到的组合输出可以表示为
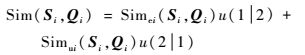
|
(22) |
式中:u(12) 和u(21) 分别为指标判断后模型的权值。权值变换为
If Radioi1<Radioi2
u(12)=1
else if Radioi1>Radioi2
u(21)=1
End
3.2 基于相似度度量指标的关联判定根据2种模型IMM作用可以得到不等长序列Si和Qi的相似度度量组合输出Sim(Si, Qi),则由多属性组成的不等序列数组Sj=(S1j, S2j, …, Smj)和Qk=(Q1k, Q2k, …, Qmk)的相似度可以根据式(6) 和式(7) 得到:
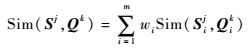
|
(23) |
式中:j、k为数组序数; m为属性个数; Sim(Sj, Qk)为不等长量测数据在m个属性共同作用下关于目标身份的综合相似度,将其作为关联判定的指标,采用最大相似度关联准则和门限检测进行关联判定。
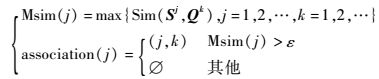
|
(24) |
式中:Msim (j)为第j个查询序列数组与所有参考序列数组相似度中的最大值;association (j)为关联序号对,则经过关联判定后可以输出不等长序列数组的关联对association (j)。
4 仿真分析 4.1 仿真环境假设传感器A、B对某批目标进行量测,得到具有3类属性特征的一系列不等长序列数组,分别记为S1、S2和Q1、Q2、Q3、Q4,其中不等长序列组中的序列中均存在突变点,假设每条序列信息描述的为目标的同一模式,不出现一条序列数据描述多个目标模式的情况,而且不等长序列数组中序列的属性特征对应。
仿真数据序列data按式(25) 产生:
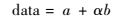
|
(25) |
式中:a为服从均匀分布的离散序列值;b为服从高斯分布的离散序列值;α为高斯分布的标准差,用来描述量测误差。在数据仿真时,首先进行标准化处理,假设文中数据已经处理好。
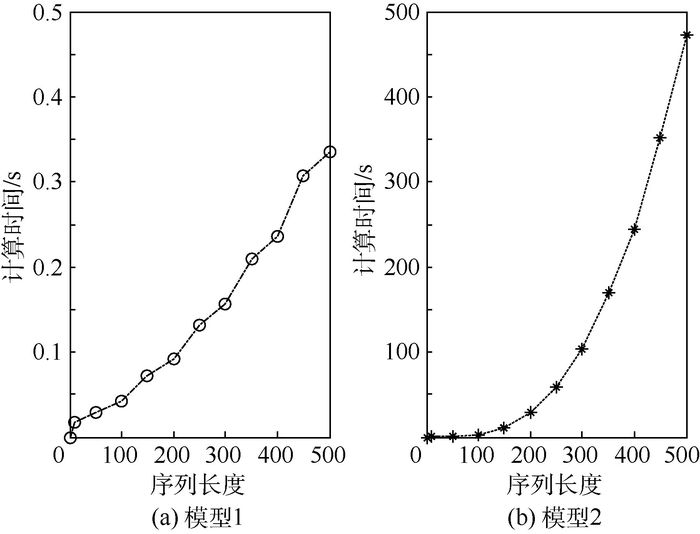
4.2 仿真实验 4.2.1 模型时间复杂度对比实验中传感器A量测的序列数据长度按步长50变化到500,由于不等长计算,相应的传感器B的量测序列长度为A的2倍,先在突变率一定的情况下,利用文中所述2种模型计算其A、B中属性对应的某2条序列的相似度所需的时间随序列长度的变化如图 3所示。
|
| 图 3 2种模型计算时间对比 Fig. 3 Comparison of calculation time between two models |
图 3中横坐标为传感器A量测序列数据长度变化,纵坐标为模型的计算时间,由图 3得知,随着序列长度增加2种模型的计算时间均增加,但是模型1的计算时间增加缓慢,数值上变化不大,而模型2的时间计算出现类指数增长趋势,十分剧烈,特别是在序列长度变得很长的时候,在序列长度较短时模型2的计算时间还是可以容忍的,说明模型2的计算时间对序列长度很敏感,在长序列度量时不宜采用模型2。
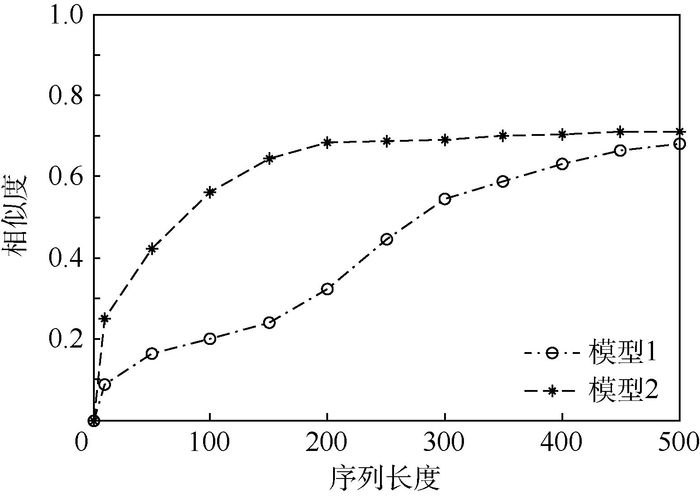
4.2.2 模型相似度计算对比同样的仿真条件,在突变点个数一定的情况下,2种模型相似度计算结果如图 4所示。
|
| 图 4 模型相似度随序列长度变化 Fig. 4 Variation of model similarity with sequence length |
由图 4得知,随着序列长度增加,2种模型的相似度计算结果提高,并在序列长度达到一定数值后稳定,而模型1的相似度增加相对于模型2较缓慢,这是由于短序列时突变率较高,模型1不能较好地处理突变点的影响,随着序列长度增加突变率减小,相似度计算提高,最后达到稳定。
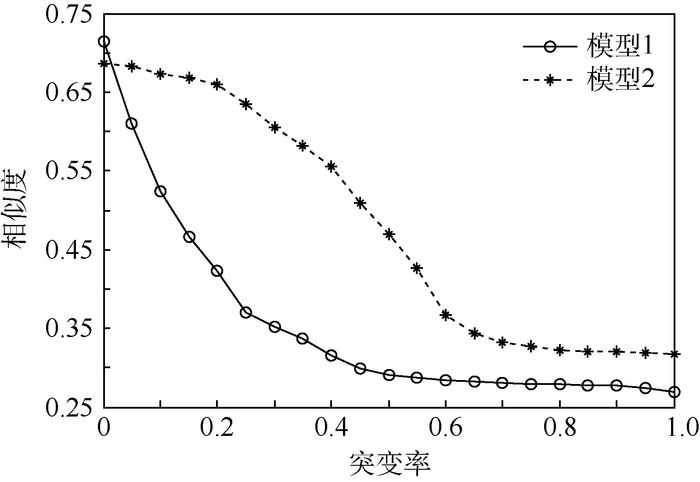
图 5给出了2种模型计算的稳定饱和相似度随突变率的变化,虽然2种模型计算的相似度都随突变率增加而减小,但是模型1的变化剧烈,而模型2在突变率一定范围内比较稳定,说明模型1对突变点的影响比较敏感,因而在短序列度量时不宜采用模型1。
|
| 图 5 模型相似度随突变率变化 Fig. 5 Variation of model similarity with fluctuant rate |
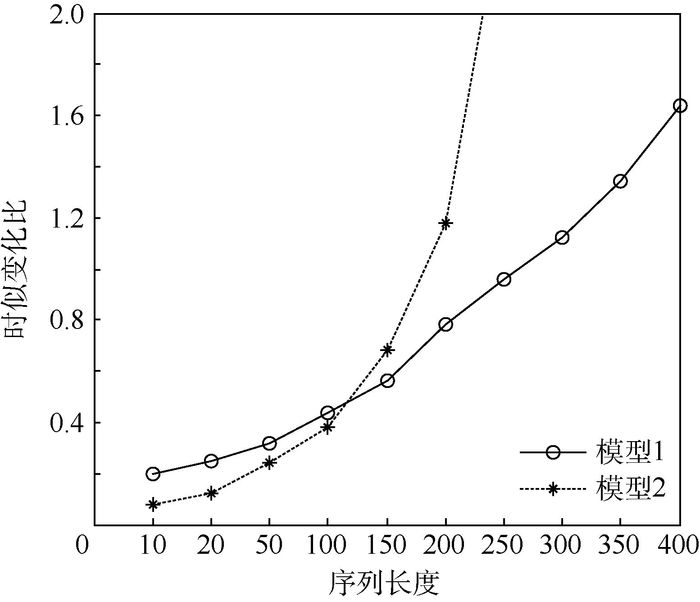
由于2种模型分别在时间复杂度和抗扰性上的不足,采用文中所述的MM变换模型对2种模型的应用条件(即2种模型切换的序列长度分界点)进行判断,在一定突变点条件下,计算2种模型的时似变化比随序列长度的变化如图 6所示。
|
| 图 6 时似变化比随序列长度的变化 Fig. 6 Variation of rate of change between time and similarity with sequence length |
由图 6得知,在序列长度较小区域模型2的时似变化比小于模型1,此时MM模型中模型2起主导作用,当序列长度变长时模型2的时似变化比增加很快又大于模型1,此时MM模型中由模型1起主导作用。可以判定2种模型时似变化比曲线的交点对应的序列长度即为模型切换的分界点,通过图 6可知在此突变率条件下模型的分界点在120附近。所以通过时似变化比能够很好地判断2种模型的应用条件,满足理论分析,并通过MM模型的共同作用,兼顾了2种模型的共同优点。
图 6得出了在一定突变点条件下2种模型的时似变化比曲线图,得到了模型转换的临界点,而当突变点变化时模型的转换临界点也应该不同,所以给出不同突变点曲线条件下的模型转换临界点变换图如图 7所示。
由图 7得知,随着突变点的增加,模型转换所需的临界点的数目也在不断增加,此时模型2的计算时间增长,短序列时模型1的计算精度又很低,但是为了提高计算的精度不得不以消耗时间为代价,所以导致序列较短时整个模型的计算时间变长,随着序列长度继续增加时,模型1工作时间又减小,而相似度在整个过程中得到了稳定。
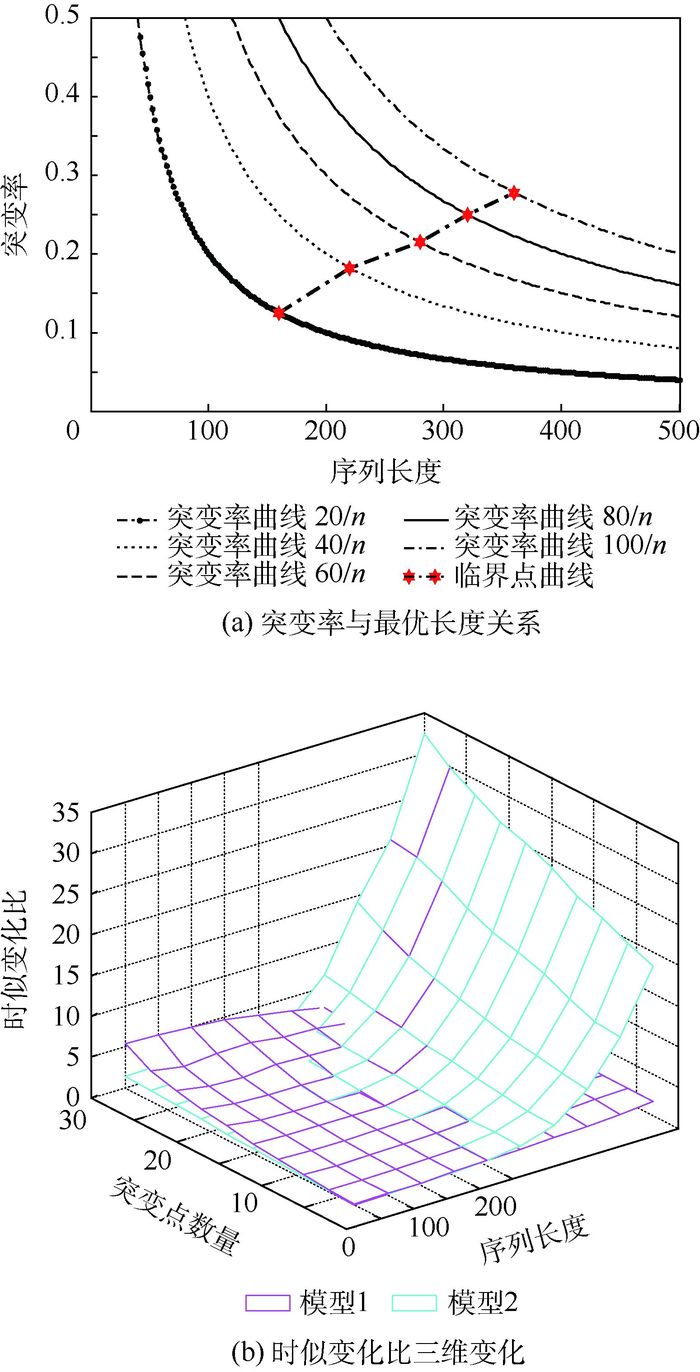
|
| 图 7 不同突变点条件下的模型转换临界点变换 Fig. 7 Change of model transformation critical point under different fluctuant points |
通过上述的模型时似变化比的计算,可以得到模型交互切换时的条件,并且可以输出度量的指标相似度,这是关联所需的,将传感器A、B量测的每条序列按照MM算法计算输出相似度,再根据式(23) 组合各不等长序列组内对应的相似度得到8组组合相似度,如表 1所示。
| 序列 | 相似度 | |||
| Q1 | Q2 | Q3 | Q4 | |
| S1 | 0.212 5 | 0.696 6 | 0.105 6 | 0.010 2 |
| S2 | 0.126 4 | 0.075 9 | 0.730 6 | 0.078 7 |
由表 1数据得知,根据式(24) 所述的关联判定准则,判定传感器A量测的不等长序列组S1及S2分别和传感器B量测的不等长序列组Q2及Q3关联。
5 结论针对单模型在不等长序列数据关联的不足,本文提出了基于多模型的不等长序列相似度挖掘的数据关联算法。通过仿真实验得到系列结论:
1) 相对于基于滑动窗口的不等长序列度量模型,基于DTW的不等长序列度量模型对复杂度计算更为敏感。
2) 相对于基于DTW的不等长序列度量模型,基于滑动窗口的不等长序列度量模型对突变率的变化更为敏感。
3) 在序列长度较短阶段MM中基于DTW的不等长序列度量模型起主导作用,在序列长度较长阶段MM中基于滑动窗口的不等长序列度量模型起主导作用,为不等长序列数据的度量和关联提供了一种可行的方法。
| [1] | AGRAWAL R, FALOUTSOS C, SWAMI A.Efficient similarity search in sequence databases[C]//Proceedings of 4th International Conference on Foundations of Data Organization and Algorithms.Berlin:Springer, 1993:69-84. |
| [2] | RAFIEI D, MENDELZON A O. Querying time series data based on similarity[J]. IEEE Transactions on Knowledge and Data Engineering, 2000, 12 (5): 675–693. DOI:10.1109/69.877502 |
| [3] | WANG C Z, WANG X Y.Multilevel filtering for high dimensional nearest neighbor search[C]//Proceedings of ACM SIGMOD Workshop on Research Issues in Data Mining and Knowledge Discovery.New York:ACM Press, 2000:37-43. |
| [4] | KORN F, JAGADISH H V, FALOUTSOS C.Efficiently supporting ad hoc queries in large datasets of time sequences[C]//Proceedings of ACM SIGMOD International Conference on Management of Data.New York:ACM Press, 1997:289-300. |
| [5] | HUHTALLA Y, KRKKINEN J, TOIVENEN H.Mining for similarities in aligned time series using wavelets[C]//Proceedings of Data Mining and Knowledge Discovery:Theory, Tools, and Technology.Orlando:[s.n.], 1999:150-160. |
| [6] |
张海勤, 蔡庆生. 基于小波变换的时间序列相似模式匹配[J].
计算机学报, 2003, 26 (3): 373–377.
ZHANG H Q, CAI Q S. Time series similarity querying based on wavelets[J]. Computer Journal, 2003, 26 (3): 373–377. (in Chinese) |
| [7] | KEOGH E.Data mining and machine learning in time series database[C]//Proceedings of the 5th Industrial Conference on Data Mining (ICDM).Leipzig:[s.n.], 2005. |
| [8] | KEOGH E, CHAKRABARTI K, PAZZANI M, et al. Dimensionality reduction for fast similarity search in large time series databases[J]. Journal of Knowledge and Information Systems, 2001, 3 (3): 263–286. DOI:10.1007/PL00011669 |
| [9] | SANG W K, SANGH Y P, WEALEY W C.An Index-based approach for similarity search supporting time warping in large sequence databases[C]//Proceedings 17th International Conference on Data Engineering.Washington, D.C.:IEEE Computer Society, 2001:607-614. |
| [10] | THANNWIN R, BILSON C, KEOGH E.Searching and mining trillions of time series subsequences under dynamic time warping[C]//Proceedings of the 18th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.New York:ACM Press, 2012:262-270. |
| [11] | KEOGH E.Exact indexing of dynamic time warping[C]//Proceedings of the 28th International Conference on Very Large Databases.San Francisco:Morgan Kaufmann, 2002:406-417. |
| [12] | RATHT M, MANMATHA R.Lower bounding of dynamic time warping distances for multivariate time series:Technical ReportMM-40[R].Amherst:Center for Intelligent Information Retrieval Technical Report, University of Massachusetts, 2003. |
| [13] | KEOGT E, PAZZANI M.Derivative dynamic time warping[C]//Proceedings of the 1st SIAM International Conference on Data Mining.Chicago:SIAM Press, 2001:209-211. |
| [14] | KEOGH E, CHAKRABARTI K, PAZZANI M. Locally adaptive dimensionality reduction for indexing large time series databases[J]. ACM Transactions on Database Systems, 2002, 27 (2): 188–228. DOI:10.1145/568518.568520 |
| [15] | BERNDT D, CLIFFORD J.Using dynamic time warping to find patterns in time series[C]//AIAA 94 Workshop on Knowledge Discovery in Databases.Reston:AIAA, 1994:359-370. |
| [16] | BAR-SHALOM Y, FORTMANN T E. Tracking and data association[M]. San Diego: Academic Press, 1988: 125-127. |



