主成分分析(Principal Component Analysis, PCA)是一种重要的数据分析与降维工具,它在科学与工程领域都有着广泛的应用。然而,由于传统PCA中的主成分(Principal Component, PC)是所有原始变量的线性组合,即PC载荷一般都是非零的[1]。因此,很难对与主成分相关的原始因素进行解释。而稀疏主成分分析就是为了解决主成分的这一缺陷而提出的,它使得PC载荷中零元素的个数变多,使主成分的可解释性增强。
当需要计算k(>1) 个稀疏主成分时,主要有2种做法:第1种做法是依次求单个主成分,即求解“单个稀疏主成分”模型,并通过压缩的(deflated)数据矩阵或数据协方差阵来依次获得更多的稀疏主成分,包括基于LASSO(Least Absolute Shrinkage and Selection Operator)约束的投影梯度法(SCoTLASS)[2]、稀疏主成分分析的半定规划直接表述法(DSPCA)[3]、基于正则化奇异值分解模型的稀疏主成分分析(sPCA-rSVD)[4]、贪心法[5-6]、单位步长条件梯度法(ConGradU)[7]、拉格朗日对偶法[8]和期望最大化稀疏主成分分析(EMPCA)[9]等。第2种做法是同时求多个主成分,即建立合适的优化模型一次获得多个稀疏主成分,包括稀疏主成分分析法(SPCA)[1]、广义幂法(Gpower l1, k, Gpower l0, k)[10]、稀疏主成分分析的增广拉格朗日函数法(ALSPCA)[11]和块坐标下降稀疏主成分分析法(BCD-SPCA)[12]等。虽然在给定不同的稀疏性参数下,依次求解单个主成分较为容易,但这种计算方式会产生累积误差,而同时计算多个主成分则减少了累积误差,并且这类做法对解决大规模稀疏PCA问题更有效且实用[12]。因而研究同时求多个稀疏主成分的算法具有应用价值。
本文提出了基于l1正则化秩k矩阵逼近的稀疏PCA模型,并设计了求解该模型的块坐标下降法(BCD-sPCA-rSVD)。该算法的主要思想是利用块坐标下降法把变量按坐标分成2k个块,当固定其他2k-1个坐标块的变量时,求解关于单个坐标块的子问题并给出子问题的显式解,循环地求解这些子问题直至满足终止条件。同时本文还分析了BCD-sPCA-rSVD的计算复杂度并证明其是收敛的。最后的数值仿真结果表明了该算法的可行性与有效性。
本文假设所有的向量都是列向量。这里列出文中常用的记号与术语。
记号Rn×p和sgn(·)分别为n×p维实矩阵和逐分量符号算子。v为向量,它的第i个分量为vi。V为矩阵,它的第i列用向量vi表示。符号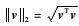
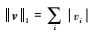
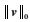
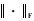
本节主要对与BCD-sPCA-rSVD密切相关的3种稀疏PCA算法SPCA、sPCA-rSVD与BCD-SPCA进行简单的回顾与说明。
1.1 SPCA与sPCA-rSVD的模型与算法Zou和Hastie[1]在2006年提出的SPCA,它的模型是先将PCA表述成回归型的优化问题,并添加关于回归系数的LASSO[13](l1范数)惩罚项,即
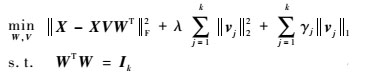
|
(1) |
其中:正参数γj(j=1, 2, …, k)用来控制载荷vj的稀疏度;Ik为k阶单位矩阵。对于n<p的数据集,要求l2范数前的参数λ>0;当n>p时,参数λ的设置是不必要的,取λ=0。
对于模型(1),SPCA利用块坐标下降法将模型(1) 的变量分成2个坐标块,即W和V,当固定其中一个坐标块W(或V)的变量时,求解关于另外一个坐标块V(或W)的子问题,而求解关于V的子问题又可转化为求解k个独立的关于V的列向量vj的子问题,交替地求解关于V和W的子问题直至终止,最后将vj(j=1, 2,…, k)单位化可得到稀疏的PC载荷。SPCA的优点是它的模型可将PCA与回归型问题建立联系,即求解去掉LASSO惩罚项的模型(1) 就可得到主成分,并且对于不同类型的数据集(n>p与n<p),SPCA都具有较低的计算复杂度[1]。
Shen和Huang[4]在2008年提出了sPCA-rSVD,此模型首先利用了数据矩阵奇异值分解与PCA的联系,由秩1矩阵逼近得到第一主成分,然后在对应的目标函数中添加正则化项(l1、l0范数等)来得到稀疏的载荷,即
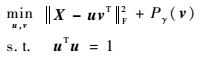
|
(2) |
其中:正则化项Pγ(v)为l1或l0范数等,γ为控制载荷v的稀疏度参数。一般来说,要求载荷v是单位向量,然而这一约束使得求解目标中含有关于v的惩罚项的模型变得困难,因此模型(2) 是对v和u的一个尺度变换,使u为单位向量而v没有任何约束限制。
sPCA-rSVD也是利用块坐标下降法将模型(2) 的变量分成u和v这2个坐标块,当固定其中一个坐标块的变量时,求解关于另外一个坐标块的子问题,交替地求解关于这2个坐标块的子问题直至终止。当正则化项为l1范数时(sPCA-rSVD-soft),sPCA-rSVD中子问题的求解较为简单(主要的计算任务包括简单的线性回归和逐分量阈值),但是sPCA-rSVD依次求解主成分的计算方式会产生累积误差。
1.2 BCD-SPCA的模型与算法Zhao等[12]在2015年提出了BCD-SPCA,它考虑了含有PC载荷的l1或l0范数约束的数据矩阵的奇异值分解模型,即
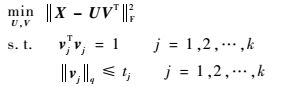
|
(3) |
其中:q=0或1;tj为控制第j个载荷vj的稀疏度参数。首先,该算法利用块坐标下降法将变量U和V按列分成2k个块,即v1, u1, v2, u2, …, vk, uk,每个vj(或uj, j=1, 2, …, k)代表一个坐标块,并将目标函数重新表述为
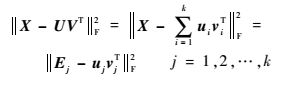
|
其中:
本文将模型(2) 推广至秩k矩阵逼近,以便同时求k个稀疏主成分,此外将u是单位向量的约束还原成载荷vj是单位向量的约束,并采用BCD-SPCA的分块模式,设计了求解l1正则化秩k矩阵逼近问题的块坐标下降法。该算法的子问题的求解比BCD-SPCA简单。
2 秩k矩阵逼近的块坐标下降法本节先提出了基于l1正则化秩k矩阵逼近的稀疏PCA模型,并设计了求解该模型的块坐标下降法,同时还分析了该算法的计算复杂度与收敛性。
2.1 模型与算法首先提出如下基于l1正则化秩k矩阵逼近的稀疏PCA模型,即
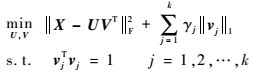
|
(4) |
其中:正参数γj(j=1, 2, …, k)的含义与模型(1) 中的相同。由于求解既含有稀疏性的条件,又有正交性约束的模型是非常困难的[10],因此大多数的稀疏PCA模型并没有要求载荷的正交性,如模型(1)~模型(3)。鉴于此,在模型(3) 中,取q=1,把关于vj的稀疏性条件放在目标中作为正则化项并保留vj是单位向量的约束即得模型(4)。因此,模型(4) 可看成是模型(3) 的惩罚版本。同时,sPCA-rSVD-soft的模型可以看作是模型(4) 在k=1时的特例(此时将约束条件变成u为单位向量即可)。
对上述模型,本文采用BCD-SPCA的分块模式,并利用块坐标下降法求解该问题。具体地,首先将目标函数等价表述为
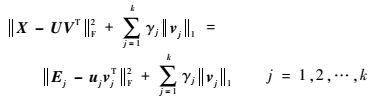
|
其中:
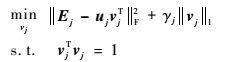
|
(5) |
当固定除uj以外的其他坐标块的变量时,得到关于uj的子问题,即
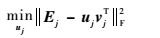
|
(6) |
为了方便表述,省去Ej、uj、vj、γj的下角标,用E、u、v、γ来表示。由于
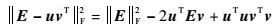
|
则子问题(5) 等价地表述为关于v在单位球上极小化二次函数加上l1范数,即
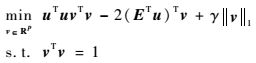
|
(7) |
因为vTv=1,从而子问题(6) 可等价表述为关于u的无约束优化问题,即
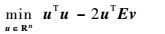
|
(8) |
定理1和定理2给出了子问题(7) 和子问题(8) 的显式解。
定理1 当Sγe(2ETu)≠0时,子问题(7) 的解为

|
证明 将问题(7) 的约束条件代入问题(7) 的目标函数,得到问题(7) 的最优解与式(9) 的相同。
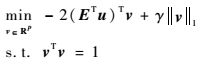
|
(9) |
再根据Sγe(2ETu)≠0和文献[7]中命题14类似的方法,可以证明式(9) 有唯一的最优解
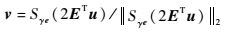
|
证毕
定理2 子问题(8) 的最优解为u*=Ev。
BCD-sPCA-rSVD就是利用上面所介绍的分块模式,并按照v1, u1, v2, u2, …, vk, uk的次序循环地求解关于vj和uj的子问题直至满足终止条件。BCD-sPCA-rSVD的伪码描述见算法1。
算法1 稀疏PCA的BCD-sPCA-rSVD算法
输入:数据矩阵X,稀疏主成分的个数k,稀疏度参数γj(j=1, 2, …, k)。
1. 给定初始点V0, U0
2. repeat
3. for j=1, 2, …, k do
4. 计算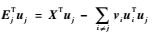
5. 求解关于vj的子问题(5) 来更新vj,即令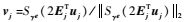
6. 计算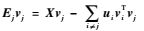
7. 求解关于uj的子问题(6) 来更新uj,即令uj=Ejvj
8. end for
9. until stopping criterion satisfied
输出:稀疏主成分载荷v1, v2, …, vk。
由于BCD-sPCA-rSVD采用了与BCD-SPCA相同的分块模式,因此在算法1的第9行中,采用与BCD-SPCA相同的终止条件,即U或V的更新率小于给定阈值,或算法的迭代次数达到预设的最大迭代次数时,算法终止。
虽然BCD-sPCA-rSVD与第1节中所介绍的3种稀疏PCA算法都是块坐标下降法,但从模型和算法的角度考虑,它们又有一定的区别:
1) 与SPCA相比,BCD-sPCA-rSVD的分块模式与模型均与SPCA不同。
2) 与sPCA-rSVD相比,BCD-sPCA-rSVD能同时求多个主成分,并且模型的目标函数是含有l1范数惩罚项的数据矩阵的秩k逼近,约束是要求vj为单位向量而不是uj。
3) 与BCD-SPCA相比,BCD-sPCA-rSVD的模型是把控制PC载荷的稀疏性条件作为目标函数的惩罚项,而不是作为约束条件。
2.2 计算复杂度分析下面讨论BCD-sPCA-rSVD的计算复杂度。为了与SPCA进行比较,本文以算法1的第3行至第8行为一次迭代。
易知该算法的计算任务主要是计算第4行与第6行中的EjTuj和Ejvj。设J为X中非零元素的个数。当计算EjTuj时,需要计算矩阵向量乘积XTuj,其计算量为J;此外还需要计算k-1次向量内积uiTuj,其计算量为(k-1)n。从而计算EjTuj的总计算量是J+(k-1)n。类似可得计算Ejvj的计算量是J+(k-1)p。从而计算EjTuj和Ejvj的总的计算复杂度是O(J+kmax(n, p))。该算法每次迭代的计算复杂度为O(Jk+max(n, p) k2)。
表 1列出了各稀疏PCA算法每次迭代的计算复杂度(包括BCD-sPCA-rSVD、SPCA以及BCD-SPCA)。这里还需强调的是,当n>p时,SPCA在第一次迭代的计算复杂度为np2+O(p3),之后每次迭代的计算复杂度均为O(p3)。由表 1可看出:
| 算法 | 计算复杂度 | |
| n>p | n<p | |
| BCD-sPCA-rSVD | O(Jk+nk2) | O(Jk+ pk2) |
| SPCA | O(p3) | O(Jk+ pk2) |
| BCD-SPCA | O(Jk+nk2) | O(Jk+ pk2) |
1) 不论对于n>p还是n<p的数据集,BCD-sPCA-rSVD的计算复杂度关于样本个数n与变量维数p都是线性的。
2) 在高维低样本数据集(n<p)下,虽然3个算法每次迭代的计算复杂度完全相同,但是BCD-sPCA-rSVD和BCD-SPCA是将变量分成2k块逐次更新,而SPCA是分成两块逐次更新,理论上前面2个算法要比SPCA收敛得更快。后文3.3节和3.4节的数值结果也很好地支持了该事实。进一步,BCD-sPCA-rSVD在每次迭代又比BCD-SPCA少求解一个方程,所以BCD-sPCA-rSVD的计算效率更高。
2.3 收敛性分析在分析BCD-sPCA-rSVD的收敛性时,首先利用约束的指示函数将原问题(4) 重新表述为无约束优化问题,即令

|
其中:fj(vj)(j=1, 2, …, k)为指示函数,定义为
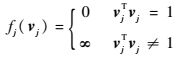
|
进一步,令

|
则原问题(4) 可等价表示为无约束优化问题
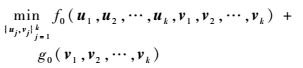
|
(10) |
问题(10) 的目标函数包括光滑的f0(u1, u2, …, uk, v1, v2, …, vk)和非光滑的g0(v1, v2, …, vk),其中非光滑部分关于vj是可分离的。而本文提出的BCD-sPCA-rSVD可看作是求解问题(10) 的块坐标下降法。令x=(u1, u2, …, uk, v1, v2, …, vk),初始点x0=(u10, u20, …, uk0, v10, v20, …, vk0),其中vj0(j=1, 2, …, k)为主成分载荷,uj0=Xvj0。定理3证明了BCD-sPCA-rSVD是收敛的。
定理3 BCD-sPCA-rSVD算法产生的点列能收敛到f的稳定点。
证明 ① 根据水平集的定义可知,L0={x:f(x)≤f(x0), vjTvj=1, j=1, 2,…, k},易知L0是紧的且f(x)在L0上连续。② 因为f0的定义域为开集且在该定义域上f0是Gateaux可微的,则根据文献[14]中的引理3.1中函数正则的判定条件,f(x)正则。③ 由定理1知子问题(7) 有唯一解,因此子问题(5) 也有唯一解;而子问题(6) 的目标函数关于uj是严格凸的,所以子问题(6) 也有唯一解。根据条件①、②、③,并由文献[14]中的定理4.1(c)可知,BCD-sPCA-rSVD算法产生的点列收敛于f的稳定点。证毕
3 数值结果与分析为了验证BCD-sPCA-rSVD的可行性与有效性,本文将BCD-sPCA-rSVD应用到各种数据集中,包括真实数据集(Pitprop,Colon Cancer,20Newsgroups)和合成数据,并与其他已有的稀疏PCA算法进行比较。本文中的所有数值实验均是在处理器为因特尔双核2.20 GHz的计算机上运行,实验所需的代码均利用MATLAB 2010a软件编写。
BCD-sPCA-rSVD中,初始点V0的每一列为主成分载荷,U0=XV0,控制最大迭代次数为1 000,U、V的更新率均取10-6。如下各实验中,这些参数的取值均保持不变。
3.1 Pitprop数据本节利用Jeffers在1967年引进的Pitprop数据[15]来验证BCD-sPCA-rSVD算法的性能。Pitprop数据包含180个样本,13个变量,即n=180, p=13。它是主成分存在解释困难的最为经典的数据集,该数据集的前6个主成分载荷中没有零元素。本次实验与BCD-sPCA-rSVD比较的算法包括SPCA[1]、SCoTLASS[2]、DSPCA[3]、sPCA-rSVD-soft[4]、Gpower(Gpowerl1, k)[10], ALSPCA[11]以及BCD-SPCA[12]。对于BCD-sPCA-rSVD,取原问题(4) 中的γ1~γ6依次为0.6, 0.6, 0.6, 1.0, 1.0, 1.0。
表 2为Pitprop数据下PCA与各稀疏PCA算法的性能指标。其中第2列的稀疏度指载荷中零元素的个数(当元素绝对值小于阈值0.001时,即截断为0)。第3列表示非正交性,设任意2个载荷vi与vj之间的夹角为αij,则非正交性为|90-αij|的最大值。显然该值越小,表明正交性越好。第4列的相关性指各主成分之间相关系数绝对值的最大值。第5列的PEV指前k个稀疏主成分的调整方差和占所有主成分方差和的百分比,它是评价稀疏PCA算法的重要指标。本节采用Zou和Hastie[1]提出的方法来计算稀疏主成分的PEV。最后一列指数据矩阵X的相对重构误差RRE,它是从数据恢复重构的角度来评价算法的性能。文献[12]给出了RRE的计算方法。
| 算法 | 稀疏度 | 非正交性 | 相关性 | PEV/% | RRE/% |
| PCA | 0 | 0 | 0 | 86.94 | 36.06 |
| DSPCA | 63 | 13.63 | 0.57 | 72.46 | 47.71 |
| Gpower | 63 | 17.88 | 0.51 | 75.04 | 45.89 |
| SCoTLASS | 27 | 0.32 | 0.44 | 78.24 | 49.24 |
| ALSPCA | 63 | 0 | 0.30 | 73.32 | 45.37 |
| sPCA-rSVD-soft | 53 | 14.76 | 0.46 | 76.59 | 46.76 |
| SPCA | 60 | 0.86 | 0.40 | 75.82 | 44.48 |
| BCD-SPCA | 63 | 20.05 | 0.40 | 75.86 | 44.19 |
| BCD-sPCA-rSVD | 63 | 1.51 | 0.28 | 75.13 | 44.18 |
表 2表明,BCD-sPCA-rSVD得到的主成分的载荷稀疏度高,有较小的相关系数与较高的PEV,且非正交性的表现优于DSPCA、Gpower、sPCA-rSVD-soft与BCD-SPCA;在数据恢复重构方面,BCD-sPCA-rSVD的RRE值与BCD-SPCA和SPCA的近似相等,且明显小于其他稀疏PCA算法,进一步验证了同时求多个主成分可以降低计算所产生的累积误差这一事实。
3.2 合成数据考虑Zou和Hastie[1]提出的人工合成数据,本文首先要定义3个变量:V1~N(0, 290), V2~N(0, 300), V3=-0.3V1+0.925V2+ε, 其中ε~N(0, 1)、V1、V2与ε独立。然后通过上述3个变量生成如下10个观测变量:

|
其中εij~N(0, 1) 且εij是相互独立的(j=1, 2, 3;i=1, 2, …,10)。由如上关系可计算出变量V1、V2与V3的方差依次为290、300与283.8。与这3个变量相关的观测变量的个数分别为4、4、2,且最后2个观测变量仅与V3有关,而V3又与V1和V2线性相关,因此只需计算前2个主成分就能包含原始数据的大部分信息。同时作出如下推测:
1) 通过观测变量X5、X6、X7、X8来计算对应于V2的第一稀疏主成分PC1。
2) 通过观测变量X1、X2、X3、X4来计算对应于V1的第二稀疏主成分PC2。
3) 由于(X1, X2, X3, X4)与(X5, X6, X7, X8)是相互独立的,则它们所对应的稀疏主成分不相关,并且其载荷是相互正交的。
与Zou和Hastie[1]的处理方式相同,本文利用精确的协方差矩阵进行计算。此外,为了使算法能够更好地去掉主成分之间的相关性,同ALSPCA[11]的处理方式,先对数据进行预处理,即将协方差矩阵除以
| 变量 | PCA | BCD-sPCA-rSVD | SPCA(BCD-SPCA) | |||
| PC1 | PC2 | PC1 | PC2 | PC1 | PC2 | |
| X1 | -0.116 3 | -0.478 4 | 0 | -0.500 0 | 0 | -0.500 0 |
| X2 | -0.116 2 | -0.478 4 | 0 | -0.500 0 | 0 | -0.500 0 |
| X3 | -0.116 2 | -0.478 4 | 0 | -0.500 0 | 0 | -0.500 0 |
| X4 | -0.116 2 | -0.478 3 | 0 | -0.500 0 | 0 | -0.500 0 |
| X5 | 0.395 1 | -0.145 3 | 0.500 0 | 0 | 0.500 0 | 0 |
| X6 | 0.395 1 | -0.145 3 | 0.500 0 | 0 | 0.500 0 | 0 |
| X7 | 0.395 1 | -0.145 4 | 0.500 0 | 0 | 0.500 0 | 0 |
| X8 | 0.395 1 | -0.145 3 | 0.500 0 | 0 | 0.500 0 | 0 |
| X9 | 0.400 9 | 0.009 1 | 0 | 0 | 0 | 0 |
| X10 | 0.400 9 | 0.0091 | 0 | 0 | 0 | 0 |
| PEV/% | 99.72 | 80.46 | 80.46 | |||
通过表 3发现,BCD-sPCA-rSVD同其他2种算法一样,成功地验证了上述全部3个预测,进一步验证了BCD-sPCA-rSVD是可行且有效的。
3.3 Colon Cancer数据结肠癌(Colon Cancer)基因表达数据集[16]是典型的高维低样本数据。它包含62个样本(22个正常组织样本和40个癌变组织样本)和2 000个基因表达变量,即n=62, p=2 000。
由于前3个主成分的PEV已接近60%,因此在本次实验中取k=3。对于这3种稀疏PCA算法,参考ALSPCA[11]的处理方式,先对数据进行预处理,令
| 算法 | 稀疏度 | 非正 交性 |
相关性 | PEV/ % |
RRE/ % |
计算 时间/ s |
迭代 次数 |
| PCA | 0 | 0 | 0 | 58.35 | 64.54 | 1.98 | |
| SPCA | 5 370 | 22.88 | 0.49 | 46.12 | 65.48 | 4.47 | 165 |
| BCD- SPCA |
5 373 | 29.15 | 0.54 | 48.88 | 69.73 | 3.65 | 97 |
| BCD-sPCA- rSVD |
5 376 | 24.02 | 0.48 | 47.24 | 65.34 | 2.76 | 91 |
由表 4可知,BCD-rSVD所得的载荷在保持较高稀疏度与PEV情况下,需要较少的计算时间和迭代次数,并在非正交性、相关性、RRE方面与其余2种算法的表现接近一致。这些事实很好地支持了表 1中的复杂度分析结论,验证了该算法在解决高维稀疏PCA问题时的简单有效。
3.4 20Newsgroups数据20Newsgroups是一组低维高样本的数据集,它记录了100个单词在16 242篇报导中出现的频率,即n=16 242,p=100。所有的新闻报导均从全球最大的电子布告栏系统Usenet上取得。该数据集下载自http://cs.nyu.edu/roweis/data.html。
在本次实验中取k=2。与上一个实验相同,先对数据进行预处理,令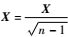
| 算法 | 稀疏度 | 非正 交性 |
相关性 | PEV/ % |
RRE/ % |
时间/ s |
迭代 次数 |
| PCA | 0 | 0 | 0 | 10.69 | 94.50 | 1.08 | |
| SPCA | 161 | 0.07 | 0.15 | 8.42 | 95.76 | 2.62 | 192 |
| BCD-SPCA | 161 | 17.64 | 0.30 | 8.71 | 95.34 | 3.11 | 58 |
| BCD-sPCA- rSVD |
166 | 0.02 | 0.09 | 8.58 | 95.60 | 2.73 | 52 |
由表 5可知,BCD-sPCA-rSVD获得的载荷在稀疏度、PEV、RRE方面与其余2种算法的表现接近一致,但在非正交性与相关性方面的表现要优于其余2种算法,并且需要的计算时间和迭代次数最少,进一步验证了该算法在解决大规模稀疏PCA问题时的有效性。
4 结论本文首次提出了基于正则化秩k矩阵逼近的稀疏PCA模型(4),并设计了求解该模型的块坐标下降法(BCD-sPCA-rSVD)。BCD-sPCA-rSVD不仅易于实现,理论分析与数值模拟还表明:
1) 该算法减少了计算的累积误差。
2) 该算法是收敛的。
3) 该算法每次迭代的计算复杂度关于样本个数n与变量维数p都是线性的,因此它可以有效地求解大规模稀疏PCA问题。
| [1] | ZOU H, HASTIE T. Sparse principal component analysis[J]. Journal of Computational and Graphical Statistics, 2006, 15(2): 265–286. DOI:10.1198/106186006X113430 |
| [2] | TRENDAFILOV N T, JOLLIFFE I T. Projected gradient approach to the numerical solution of the SCoTLASS[J]. Computational Statistics and Data Analysis, 2006, 50(1): 242–253. DOI:10.1016/j.csda.2004.07.017 |
| [3] | D'ASPREMONT A, GHAOUI L E, JORDAN M I, et al. A direct formulation for sparse PCA using semidefinite programming[J]. SIAM Review, 2007, 48(3): 434–448. |
| [4] | SHEN H, HUANG J Z. Sparse principal component analysis via regularized low rank matrix approximation[J]. Journal of Multivariate Analysis, 2008, 99(6): 1015–1034. DOI:10.1016/j.jmva.2007.06.007 |
| [5] | MOGHADDAM B, WEISS Y, AVIDAN S.Spectral bounds for sparse PCA:Exact and greedy algorithms[C]//Advances in Neural Information Processing Systems.Montreal:Neural Information Processing System Foundation, 2006:915-922. |
| [6] | D'ASPREMONT A, BACH F R, GHAOUI L E. Optimal solutions for sparse principal component analysis[J]. Machine Learning, 2008, 9(7): 1269–1294. |
| [7] | LUSS R, TEBOULLE M. Conditional gradient algorithms for rank-one matrix approximations with a sparsity constraint[J]. SIAM Review, 2013, 55(1): 65–98. DOI:10.1137/110839072 |
| [8] | LUSS R, TEBOULLE M. Convex approximations to sparse PCA via Lagrangian duality[J]. Operations Research Letters, 2011, 39(1): 57–61. DOI:10.1016/j.orl.2010.11.005 |
| [9] | SIGG C, BUHMANN J.Expectation-maximization for sparse and nonnegative PCA[C]//Proceedings of the 25th International Conference on Machine Learning.NewYork:ACM, 2008:960-967. |
| [10] | JOURNEE M, NESTEROV Y, RICHTARIK P, et al. Generalized power method for sparse principal component analysis[J]. Journal of Machine Learning Research, 2010, 11(2): 517–553. |
| [11] | LU Z S, ZHANG Y. An augmented Lagrangian approach for sparse principal component analysis[J]. Math Program Series A, 2012, 135(1-2): 149–193. DOI:10.1007/s10107-011-0452-4 |
| [12] | ZHAO Q, MENG D Y, XU Z B, et al. A block coordinates descent approach for sparse principal component analysis[J]. Neurocomputing, 2015, 153(4): 180–190. |
| [13] | TIBSHIRANI R. Regression shrinkage and selection via the LASSO[J]. Journal of the Royal Statistical Society Series B, 1996, 58(3): 267–268. |
| [14] | TSENG P. Convergence of a block coordinates descent method for nondifferentiable minimization[J]. Journal of Optimization Theory Apply, 2001, 109(3): 475–494. DOI:10.1023/A:1017501703105 |
| [15] | JEFFERS J N R. Two case studies in the application of principal component analysis[J]. Applied Statistics, 1967, 16(3): 225–236. DOI:10.2307/2985919 |
| [16] | ALON U, BARKAI N, NOTTERMAN D A, et al. Broad patterns of gene expression revealed by clustering of tumor and normal colon tissues probed by oligonucleotide arrays[J]. Proceedings of the National Academy of Sciences of the United States of America, 1999, 96(12): 6745–6750. DOI:10.1073/pnas.96.12.6745 |



