流固耦合传热(Conjugate Heat Transfer,CHT)广泛存在于机械、动力、能源、航空航天、化工和核工等工程领域。它一方面指流体与固体内传热过程通过流固交界面的位移、形变、传热和相变等作用相互耦合,另一方面指流固交界面上流动、辐射和烧蚀等不同物理过程相互耦合。Stokos[1]、Hooper[2]、Kazemi-Kamyab[3]等开发了将流体及固体内所有物理过程进行瞬态紧耦合算法,能使计算结果与实验结果高度吻合。但是,该瞬态紧耦合计算需要消耗大量的计算资源,难以用于解决实际复杂工程问题。为此,研究者们从不同程度上解除流固之间或各物理过程之间的耦合关系,开发了具有不同计算效率、不同计算精度的求解方案。
根据问题的特征,有些研究者近似认为在计算时间内,某些参数的状态是不变的,进而直接将瞬态问题转化为稳态问题[4-5]。对于绝大多说不能通过准稳态处理直接转化为稳态问题的瞬态问题,有些研究者主张保留耦合的非稳态特性,提出各部分分别进行瞬态求解,并通过边界条件、参数值及活动网格等方式进行实时信息交互的瞬态松耦合传热问题(loose-coupled transient conjugate heat transfer problems)的求解。如Bauman[6]和Kazemi-Kamyab[7-8]等针对高超声速流中固体表面带辐射及烧蚀相变过程的流固耦合强制对流传热问题,提出将流体Navier-Stokes方程与固体导热、辐射及烧蚀相变过程分别进行瞬态求解,并利用流体数值计算结果对其他求解方程的边界温度和热流加以修正,直至迭代收敛。Lohner等[9]针对飞机气弹分析中带固体形变的流固耦合传热问题,将流体Navier-Stokes方程及固体导热和应变方程分别求解,并利用流体数值计算结果对其他求解方程的边界温度和热流加以修正,同时利用固体应变方程的计算结果修正流体耦合边界位置和速度边界条件,直至迭代收敛。
考虑到通常情况下流固耦合传热过程中流体流动过程特征时间往往与固体传热过程特征时间相差3~4个数量级,有些研究者进一步提出对各物理过程使用不同的瞬态时间步长的瞬态松耦合算法,以提高计算效率。如Li[10]和Miller[11]等分别利用该算法求解火箭发动机点火过程及高超声速流固耦合的应力分析问题。
但是研究结果表明,上述瞬态松耦合算法中均包含小特征时间的瞬态流场求解,计算效率的提高非常有限,无法满足实际工程中遇到的千秒级长时间耦合问题的求解效率需求。
为此,有些研究者提出了基于准稳态流场的松耦合算法,即近似认为在整个流固耦合传热过程中,流场处于若干个准稳态,每一个准稳态的流场都使用稳态Navier-Stokes方程求解。如Kontinos[12]结合二维边界单元法和高超声速计算流体力学(CFD)算法的松耦合算法,分析了高超声速流与机翼前缘的耦合传热问题。Chen[13]和Zhang[14]等交替进行稳态流场计算与固体烧蚀和瞬态导热的松耦合算法计算了带烧蚀的流固耦合传热问题。研究结果表明该算法可以大大提高计算效率,但是计算结果偏差较大,究其原因主要是其将流场与其他部分完全隔离的处理方法与实际耦合关系间的偏差较大。另外,该算法中主要通过流场更新的方式来更新流固耦合壁面上的热流密度,而该参数不仅受流场的影响,还与固体瞬态温度场紧密相关,因此为更加贴合实际情况往往要求频繁执行流场更新,进而严重影响了其计算效率的提高程度。
为此,本文进一步针对千秒级长时间流固耦合传热过程求解问题,提出一种基于准稳态流场的全局瞬态紧耦合传热的新型松耦合算法,并以管内空气强制对流瞬态传热过程为例,利用Fluent软件将该算法与瞬态紧耦合算法的计算结果进行对比分析,验证该算法的优越性。
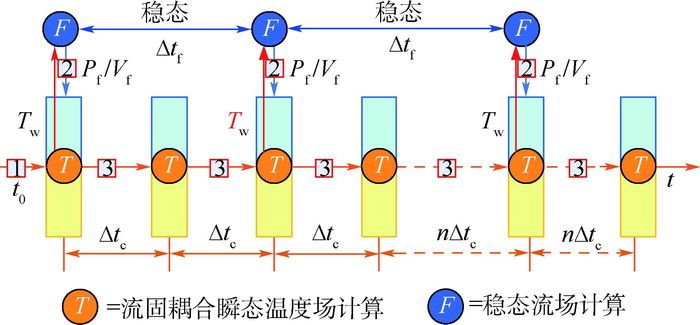
1 总体算法以基本CHT问题为例,即流体区域发生流动和传热过程,固体区域只发生传热,不包含辐射、烧蚀及固体应力形变等其他物理过程,本文提出的基于准稳态流场的全局瞬态紧耦合传热的新型松耦合算法,即利用稳态算法更新流场,而对流体和固体的能量方程进行紧耦合瞬态求解,具体计算流程如图 1所示。
|
| T—温度; Pf—流体压力; Vf—流体速度; Δtf—稳态流场更新步长; Δtc—瞬态时间步长; n—瞬态迭代步数; Tw—壁面温度 图 1 新型松耦合算法流程示意图 Fig. 1 Flow diagram of new loosely coupled algorithm |
1) t0时刻:初始化流体和固体区域温度场。
2) 更新流场:单独对流体区域稳态流场进行求解,即将流固耦合壁面设为固定温度边界,联立求解流体区域稳态动量、湍流及能量方程,获得稳态流场。
3) 瞬态温度场计算:同时对流体区域和固体区域进行瞬态传热计算,即将流固耦合壁面设为传热耦合边界,联立求解流体及固体区域瞬态能量方程,获得每时刻温度场分布情况,直至下一个流场更新时刻。
4) 重复2)、3) 两步,交替进行流场更新和瞬态温度场计算,直至计算终止时刻t。
从图 1中可以看出,该算法保留了流固耦合问题中能量方面强耦合特性,但整个算法是以瞬态温度场时间步长向前推进,仅在一个或多个时刻穿插进行稳态流场更新,进而避免了瞬态流场计算过于耗时的问题。
同时,与一般基于准稳态流场的松耦合算法不同,本算法中流场稳态计算不是用来更新流固耦合壁面的热流密度,而是负责为流固耦合瞬态传热计算提供流体区域的速度场和压力场。因而,只有当边界条件发生大的变化,严重影响了流体区域流场分布,并使流固耦合界面上对流换热系数(努塞尔数)发生较大变化时,才需要执行流场更新步骤。
为了解决流场更新时刻确定这一算法实际应用中的重要问题,本文提出了基于努塞尔数阈值的流场更新时刻确定算法。根据本文算法的瞬态传热过程算法,可以将传热计算误差的阈值转化为努塞尔数阈值。在瞬态计算中利用努塞尔数的工程经验公式或量纲分析结果来监测努塞尔数变化情况,从而确定流场更新时刻。由于努塞尔数阈值由计算精度要求决定,努塞尔数实际变化情况由实例工况决定,所以流场更新频率由这两者共同决定。
在应用中,除了可以利用努塞尔数经验公式直接监测努塞尔数的变化情况,也可以先行对努塞尔数经验公式进行化简,用便于监测的其他参数的阈值作为流场更新阈值。例如,对管槽内层流强制对流换热过程努塞尔数工程经验公式为列齐德-泰特公式:

|
(1) |
式中:l和d分别为管长和管径;Nuf、Ref和Prf分别为努塞尔数、雷诺数和普朗特数;ηf为流体平均温度下的流体黏性系数;ηw为在管壁温度下的流体黏性系数。
从式(1) 中可以看出,流体和固体的温度主要通过影响流体的物性参数影响对流换热系数。若忽略流体物性随温度的变化,则努塞尔数仅与来流速度V有关,C为常数,即
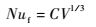
|
(2) |
为此,根据式(1) 和式(2) 即可获得要保证换热强度保持在一定偏差范围内时来流速度的最大变化幅度,进而确定流场更新时刻。假如整个计算过程中流体出入口边界条件和流速均不变,则求得稳态流场后不需再更新流场。
2 控制方程及数值算法依据上述新型松耦合总体算法,确定基本CHT问题主要控制方程及数值算法如下。
2.1 准稳态流场准稳态流场控制方程可采用k-ε湍流模型,可表示为
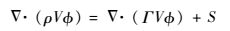
|
(3) |
式中:ρ为密度;Φ为方程变量,具体包括x、y、z 3个方向速度分量u、v、w及湍流动能k、湍流耗散率ε和温度T;Γ为各变量广义扩散系数;S为各变量源项。
针对管内空气强制对流瞬态传热问题,可按不可压缩流体,采用有限体积法对准稳态流场控制方程进行离散,并使用基本SIMPLE算法[15]解决速度与压力的耦合问题。具体计算步骤如下:
1) 假定一个速度分布,记为V0,以此计算动量离散方程中的系数和常数项。
2) 假定一个压力场p*,依次求解各方向上的动量方程,得到新的速度分布,记为V*。
3) 求解压力修正方程,得p′。
4) 据p′改进速度值V′。
6) 利用改进后的速度场V′求解那些通过源项、物性等与速度场耦合的变量,如果变量并不影响流场,则应在速度场收敛后再求解。
7) 利用改进后的速度场重新计算动量离散方程的系数,并用改进后的压力场作为下一层迭代的初值,重复上述步骤,直到获得收敛解。
2.2 流固耦合瞬态温度场在求解流固耦合的瞬态温度场时,流体区域可按准稳态流场处理,即不考虑流场的动量和湍流方程,则其控制方程式(3) 简化为仅包含温度变量,其他变量均视为定值,即
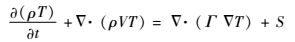
|
(4) |
固体区域控制方程以其基本导热方程表示为
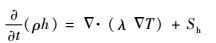
|
(5) |
式中:h为显焓;λ为导热系数;Sh为体积热源。
控制方程式(5) 等号左边第1项表示固体能量随时间的变化,右边2项分别表示传导引起的热流以及固体内部的体积热源。对于各向异性导热的,其热传导项为∇·(λlj∇T),λlj为导热率张量。
流固交界面上不考虑发生的辐射、烧蚀相变等过程,则流固交界面上满足能量连续性条件, 即温度和热流密度相等。具体控制方程式为

|
(6) |

|
(7) |
式中:Tf和λf分别为流体温度和导热系数;Ts和λs分别为固体温度和导热系数;qf和qs分别为流固交界面上流体侧和固体侧的热流密度;n为流固交界面法向量。
方程式(5)~式(7) 构成了流固耦合瞬态温度场控制方程,可以使用分区瞬态紧耦合算法进行求解。即在每个[t, t+Δt]时间步长内,完成如下计算步骤:
1) 假定耦合边界上的温度分布,作为流体区域的边界条件。
2) 对其中流体区域进行稳态求解,得出耦合边界上的局部热流密度和温度梯度,作为固体区域的边界条件。
3) 求解固体区域,得出耦合边界上新的温度分布,作为流体区域的边界条件。
4) 重复2)、3) 两步计算,直到收敛。
3 定来流强制对流加热问题分析下面以矩形不锈钢管内受一定来流工况的热空气强制对流加热的基本流固耦合传热过程为例,以Fluent商业软件瞬态紧耦合求解结果为标准,对本文算法进行一定对比分析。
具体几何模型如图 2所示,其中管长为328 mm,内壁横截面尺寸为:10.4mm×6.4mm,上下两面厚度为1.3 mm,左右两面厚度为0.95 mm。假设管道初始温度为300 K,外壁面绝热,入口为速度入口边界,空气温度为400 K,流速为2 m/s,出口为压力出口边界。

|
| 图 2 空气内加热管几何模型 Fig. 2 Geometric model of inner-air-heated tube |
为了对比分析数值计算结果,在距入口5%、27.5%、50%、77.5%及95%总长处,流体参数取流体中心线上的参数作为代表,固体参数考虑到铝管体的高效传热特性可以取管体侧竖壁中心线上的参数作为代表。在管道中心及壁面中心各取5个位置。
如前所述,由于该例中来流工况恒定,若忽略流体和固体物性随温度的变化,依据本文算法只需在初始时刻进行一次稳态流场计算,然后按一定时间步长求解流固耦合的瞬态温度场,具体该例中,本文算法瞬态温度场计算时间步长为0.5 s,Fluent软件瞬态紧耦合算法时间步长为0.05 s,两者相差一个数量级。
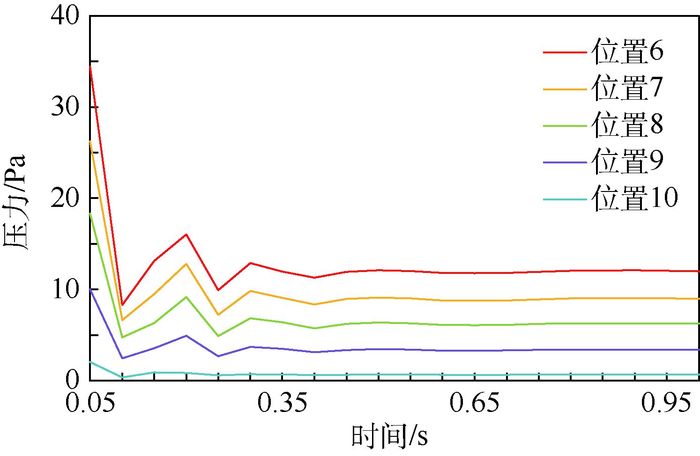
3.1 准稳态流场假设的合理性分析Fluent软件瞬态紧耦合算法获得位置6~位置10处管内流体静压值随时间变化曲线如图 3所示。从中可以看出:计算初期,各位置处流体静压均有一定波动,且距入口越远波动越不明显,约0.5 s后各位置处流体静压均基本达到稳定。
|
| 图 3 管内不同位置处空气静压变化曲线 Fig. 3 Changing curves of inner air staticpressure at different locations |
在初始时刻对流场进行稳态更新后,流场将直接达到稳定状态,即0.5 s之后状态。相对于瞬态紧耦合计算,松耦合计算跳过前0.5 s的流场发展阶段。由于该阶段远小于整个瞬态传热时长,跳过这一阶段引入的误差很小。
为此,对于入口边界流动参数变化间隔远大于该时间的耦合传热问题,本文算法中基于准稳态流场的假设是合理的。
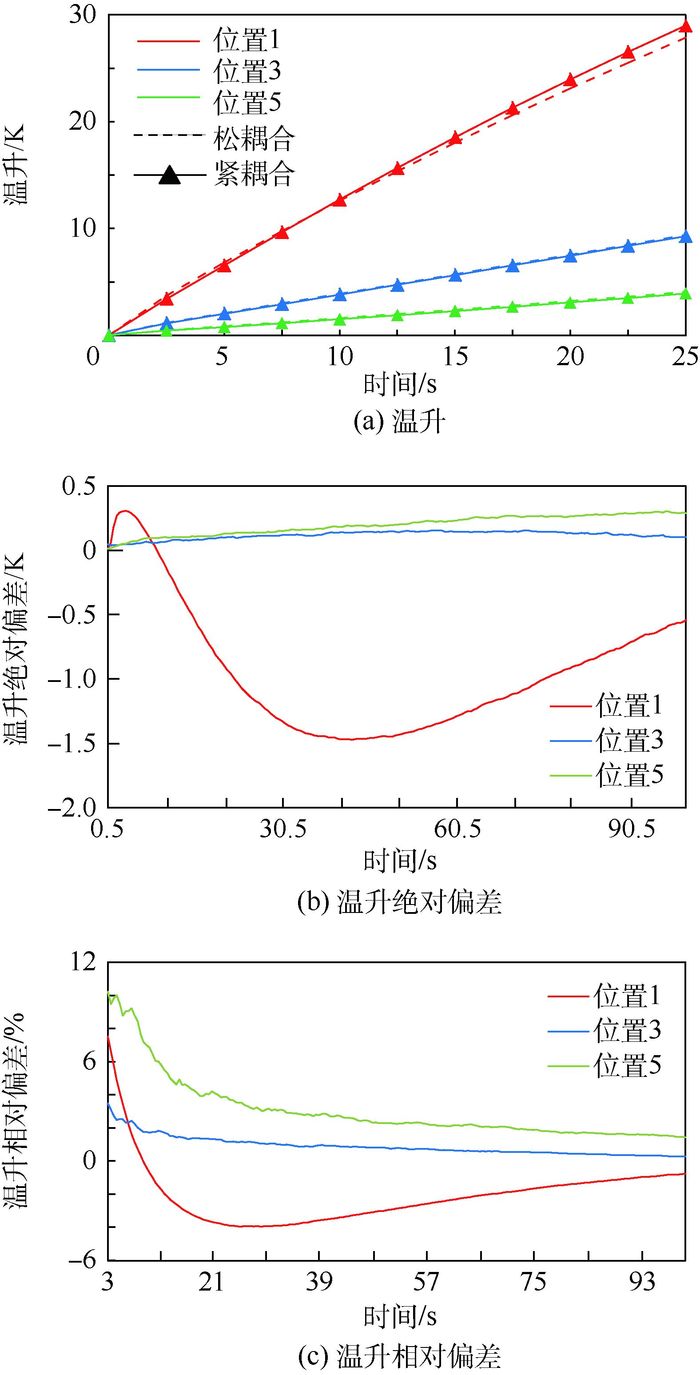
3.2 管体结构瞬态温度场对比分析图 4为紧耦合及本文算法获得管体结构1、3、5的3个位置处前25 s的温升及其绝对偏差和相对偏差的对比曲线。从中可以看出:
|
| 图 4 2种算法所得不同位置管体温升、温升绝对偏差及温升相对偏差变化曲线 Fig. 4 Changing curves of wall temperature rise, absolutedeviation of wall temperature rise and relative deviation ofwall temperature rise at different locations by two algorithms |
1) 如图 4(a)所示,与紧耦合算法相比,松耦合计算的温升总体在入口处偏低,出口处偏高,且由于出口处总体温升值较小,导致其在温升绝对偏差近似的情况下温升的相对偏差值略高。
2) 如图 4(b)所示,两者绝对偏差随着时间呈现一定波动,离入口越远波动周期越长,且入口处波动幅度最大,在42.5 s时达到最大值1.4 K左右。
3) 如图 4(c)所示,两者各位置相对偏差均在初始时刻最大,并逐渐趋近于0。如管体三处温升相对偏差25 s时均已下降到4%以内,100 s时下降到1%以内。
综上所述,定来流工况下,本文算法能够将瞬态温升过程中相对偏差控制在5%左右。
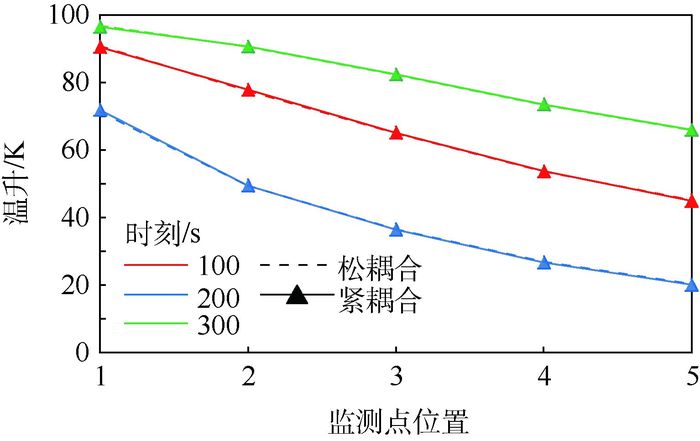
分析计算偏差的来源主要包括本文算法开始时刻跳过了流场发展阶段、并直接过渡到稳定流场的处理方式以及较大的时间步长。但是,如图 5和表 1给出的100、200及300 s时2种算法所得管体结构温升沿气流方向的分布曲线和数据所示:随着时间的推移和实际流场的不断稳定,该偏差将进一步减小,最终会统一达到该工况下稳定温度场分布。如300 s时,不同位置处管体温升的绝对偏差都已经降至0.34 K以下,满足工程实际要求。
|
| 图 5 2种算法所得不同时刻管体温升分布对比曲线 Fig. 5 Contrast curves of wall temperature rise distribution at different moments by two algorithms |
| K | |||||||||||||||
| 时刻/s | 位置1 | 位置2 | 位置3 | 位置4 | 位置5 | ||||||||||
| 紧耦合 | 松耦合 | 偏差 | 紧耦合 | 松耦合 | 偏差 | 紧耦合 | 松耦合 | 偏差 | 紧耦合 | 松耦合 | 偏差 | 紧耦合 | 松耦合 | 偏差 | |
| 100 | 71.79 | 71.24 | -0.55 | 49.43 | 49.38 | -0.05 | 36.43 | 36.53 | 0.10 | 26.72 | 26.84 | 0.12 | 20.09 | 20.37 | 0.28 |
| 200 | 90.41 | 90.78 | 0.37 | 77.80 | 77.46 | -0.34 | 65.10 | 64.89 | -0.21 | 53.68 | 53.61 | -0.07 | 44.95 | 45.08 | 0.13 |
| 300 | 96.45 | 96.79 | 0.34 | 90.62 | 90.57 | -0.05 | 82.36 | 82.20 | -0.16 | 73.44 | 73.28 | -0.16 | 65.93 | 65.80 | -0.13 |
3.3 计算效率对比分析
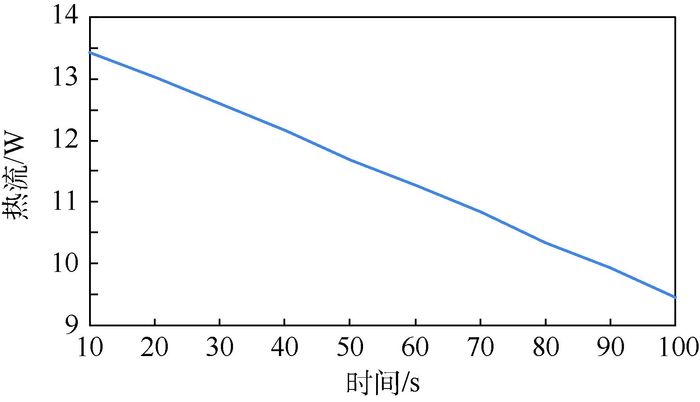
图 6给出了紧耦合算法获得的管内壁热流随时间变化曲线。从图 6中可以看出:即使在定来流工况下,流固耦合壁面上的热流密度也会随流固两者温差的变化而发生较大变化。
|
| 图 6 定来流工况下,管内壁热流随时间变化曲线 Fig. 6 Curve of inner wall heat flux variation with time under constant flow rate condition |
为此,以热流密度和温度为传递变量的传统松耦合算法,为保证瞬态温度场计算准确性,需要不断调用流场计算以更新流固耦合壁面上热流密度值。而本文算法是在准稳态流场的基础上对整个流固区域能量方程进行紧耦合计算,因此,只要流场不变就不需要更新流场,进而相对于传统松耦合算法可以进一步提高计算效率。
如上述管内定来流速度热空气连续300 s的强制对流加热问题,利用Fluent软件的实时紧耦合算法时间步长为0.05 s,计算耗时为13.5 h;本文算法只在初始时刻计算一次稳态流场,瞬态温度场时间步长为0.5 s,计算耗时为2 h,即计算时间减小到原来的14.8%。
4 结论本文针对长时间流固耦合传热(CHT)过程求解问题,提出了一种新型松耦合算法,得到如下主要结论:
1) 本文算法避免了传统松耦合算法需要不断调用流场计算以更新流固耦合壁面上热流密度值问题,只要流场不变就不需要更新流场,进而大大减小流场更新频率,进一步提高计算效率。
2) 针对该类管内定来流速度强制对流耦合传热问题,采用本文算法可以在保证瞬态温度场计算精度的情况下,将计算效率提高近一个量级,进而满足工程上对长时间流固耦合传热过程的求解需求。
3) 该管内强迫对流算例中,由边界流动参数的变化引起管内流场不稳定时间大约只有0.5 s。这与不可压流场的快速传播特性是相符的,同时也说明本文算法中基于准稳态流场的假设是具有一定适应性的,如类似不可压流体长时间耦合传热问题,只要边界流动参数阶跃变化间隔远大于0.5 s这个量级,都可以考虑采用本文算法在保证计算精度的同时提高计算效率。
| [1] | STOKOS K, VRAHLIOTIS S, PAPPOU T, et al. Development and validation of an incompressible Navier-Stokes solver including convective heat transfer[J]. International Journal of Numerical Methods for Heat & Fluid Flow, 2015, 25(4): 861–886. |
| [2] | HOOPER R W, SMITH T M, OBER C C.Enabling fluid-structural strong thermal coupling within a multi-physics environment[C]//44th AIAA Aerospace Sciences Meeting and Exhibit.Reston:AIAA, 2006:1-10. |
| [3] | KAZEMI-KAMYAB V, VAN ZUIJLEN A H, BIJL H. Analysis and application of high order implicit Runge-Kutta schemes for unsteady conjugate heat transfer:A strongly-coupled approach[J]. Journal of Computational Physics, 2014, 272: 471–486. DOI:10.1016/j.jcp.2014.04.016 |
| [4] |
曾大文, 黄开金. 非交错网格下三维准稳态激光重熔熔池数值模拟[J].
计算物理, 1999, 16(6): 616–623.
ZENG D W, HUANG K J. Numerical simulation of three dimensional quasi-steady state laser melted pools on the non-staggered grids[J]. Chinese Journal of Computational Physics, 1999, 16(6): 616–623. (in Chinese) |
| [5] |
殷鹏飞, 张蓉, 熊江涛, 等. 搅拌摩擦焊准稳态温度场数值模拟[J].
西北工业大学学报, 2012, 30(4): 622–627.
YIN P F, ZHANG R, XIONG J T, et al. An effective numerical simulation of temperature distribution of friction stir welding in quasi-steady-state[J]. Journal of Northwestern Polytechnical University, 2012, 30(4): 622–627. (in Chinese) |
| [6] | BAUMAN P T, STOGNER R, CAREY G F, et al. Loose-coupling algorithm for simulating hypersonic flows with radiation and ablation[J]. Journal of Spacecraft and Rockets, 2011, 48(1): 72–80. DOI:10.2514/1.50588 |
| [7] | KAZEMI-KAMYAB V, VAN ZUIJLEN A H, BIJL H. A high order time-accurate loosely-coupled solution algorithm for unsteady conjugate heat transfer problems[J]. Computer Methods in Applied Mechanics and Engineering, 2013, 264: 205–217. DOI:10.1016/j.cma.2013.05.021 |
| [8] | KAZEMI-KAMYAB V, VAN ZUIJLEN A H, BIJL H. Accuracy and stability analysis of a second-order time-accurate loosely coupled partitioned algorithm for transient conjugate heat transfer problems[J]. International Journal for Numerical Methods in Fluids, 2014, 74(2): 113–133. DOI:10.1002/fld.v74.2 |
| [9] | LOHNER R, YANG C, CEBRAL J, et al.Fluid-structure-thermal interaction using a loose coupling algorithm and adaptive unstructured grids[C]//Proceedings of 29th AIAA Fluid Dynamics Conference.Reston:AIAA, 1998:1-16. |
| [10] | LI Q, LIU P, HE G. Fluid-solid coupled simulation of the ignition transient of solid rocket motor[J]. Acta Astronautica, 2015, 110: 180–190. DOI:10.1016/j.actaastro.2015.01.017 |
| [11] | MILLER B A, CROWELL A R, MCNAMARA J J.Loosely coupled time-marching of fluid-thermal-structural interactions:AIAA-2013-1666[R].Reston:AIAA, 2013. |
| [12] | KONTINOS D. Coupled thermal analysis method with application to metallic thermal protection panels[J]. Journal of Thermophysics and Heat Transfer, 1997, 11(2): 173–181. DOI:10.2514/2.6249 |
| [13] | CHEN Y K, MILOS F S, GOKCEN T. Loosely coupled simulation for two-dimensional ablation and shape change[J]. Journal of Spacecraft & Rockets, 2010, 47(5): 775–785. |
| [14] | ZHANG S, CHEN F, LIU H. Time-adaptive, loosely coupled strategy for conjugate heat transfer problems in hypersonic flows[J]. Journal of Thermophysics and Heat Transfer, 2014, 28(4): 1–12. |
| [15] | AMES W F. Numerical methods for partial differential equations[M].2nd edNew York: Academic Press, 1977: 114-151. |



