液滴在平壁表面的铺展以及移动现象不仅在自然现象中广泛存在,如雨滴在树叶表面以及汽车风挡玻璃表面的润湿和滑落行为,而且在喷墨印刷、半导体元器件的制作和化妆品生产等工业过程[1-2]以及微流控芯片[3-5]等领域都有着非常重要的应用。
文献[6-8]分别在光滑表面和粗糙表面上建立了液滴的润湿模型,大量关于接触角模型和接触线移动的研究随之展开。文献[9]通过实验发现,在非理想表面接触角不是唯一的,存在接触角滞后,指出接触线发生移动的条件是接触角需增大到某个阈值θa,称为前进接触角。Daniel等[10-11]研究了在润湿滞后的状态下由表面能梯度引起的液滴运动,发现由于没能克服接触角滞后,液滴并未朝着梯度更加润湿的方向移动。但是滞后作用力在空间上是非对称的,沿梯度反方向的值要大于沿梯度方向的值,因此施加非对称的周期作用力可以使液滴朝着更加润湿的区域运动。王晓东等[12]对粗糙表面下润湿性接触角滞后的现象进行了实验研究,指出滞后张力可表示表面粗糙度对接触角滞后的影响。石自媛等[13]采用格子Boltzmann方法研究了固/液界面上润湿性梯度引起表面张力变化从而驱动液滴的运动,对速度矢量分析,发现液滴是滚动着向亲水端运动的,在疏水端液滴内部出现一个漩涡,因此在流体界面处存在较大的剪切应力。文献[14]通过数值模拟了倾斜表面液滴在润湿性梯度驱动下爬坡的过程,也得到了类似的结论。周建臣等[15]完成了液滴在超疏水表面上受迫振动的观察实验,发现在80~120Hz的驱动频率内,接触线出现显著的固着-移动现象,指出液滴在低频的外界驱动力作用下的不同响应与接触线的振荡行为密切相关。
随着对接触角润湿滞后以及接触线移动的深入研究,微流体流动机理研究也得到了学者们的重视。Walker等[16-18]针对受限系统的电润湿过程,提出了基于Hele-Shaw流的简化数值方法,同时构建了接触角饱和、滞后和黏弹运动等复杂情况的计算模型,并且通过数值方法对液滴分裂、合并和移动进行了研究。Li和Mugele[19]对交流电润湿下的接触角进行实验研究,发现随着电压的增加,直流电润湿时液滴的滞后角几乎保持不变,而交流电润湿时滞后角趋近于零,因此电场力振荡有利于接触线移动,并不影响其后退。高阳等[20]通过叉指换能器产生声表面波,实现了对水滴的驱动运动,在输入功率9W时液滴运动的速度均值为5mm/s。
虽然关于液滴收缩-铺展的动力学行为以及微流控芯片中的流体流动有较为全面的研究,但是基于超声行波驱动的平板模型液滴运动的机理研究方面还较少。笔者基于超声行波理论,构建了弹性体平板驱动模型,借助多物理场软件COMSOL对液滴运动特性进行数值模拟,首先验证了产生行波的可行性,然后分析在超声行波驱动下液滴移动的动力学行为,最后对液滴移动速度与驱动电压、驱动频率以及液滴动力黏度的关系进行探讨,为实际应用中的分区或分片压电陶瓷的生产制作以及在弹性体平板表面驱动液滴运动提供了一定的理论基础和依据。
1 数学模型 1.1 液滴润湿行为当液滴被放置在固体表面时,接触角是指固体表面和液滴表面之间的角度,表征固体表面浸润行为。图 1所示为液滴在水平固体表面上的接触角与表面张力,接触角描述了3个表面张力之间的平衡关系,三相之间的能量关系可通过杨氏方程[6]进行描述,即
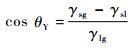
|
(1) |

|
| 图 1 液滴在水平固体表面上的接触角与表面张力 Fig. 1 Contact angle and surface tensions of a droplet on horizontal solid surface |
式中:θY为静态接触角; γsg、γsl和γlg分别为固/气界面、固/液界面和液/气界面的表面张力。
1.2 液滴运动方程基于质量守恒原理,液滴中任一点流体密度均满足连续方程[21]为
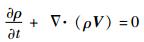
|
(2) |
式中:ρ为液滴密度;t为时间;V为液滴速度矢量。
对不可压缩的定常流动,连续方程简化为
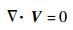
|
(3) |
基于动量守恒原理,液滴流动通常是不可压缩的定常流动,满足Navier-Stokes方程:
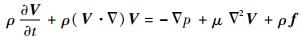
|
(4) |
式中:p为压力;μ为动力黏度;f为单位质量液滴的体积力。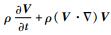
对于有限长度的弹性体平板,由于存在端反射问题,因此比较困难产生较为理想的行波[22],只能产生驻波。考虑到在平板上产生理想行波,需要在平板的另一端加上吸振器或者吸波材料,从而改善反射波的影响。通常在实际应用中,由于弹性体平板材料的内部阻尼会产生能量耗散作用,同时平板表面的液滴吸收行波的驱动作用,使超声行波的能量逐渐衰减,因此端反射回来的机械波也会大大减弱。根据波的叠加原理,平板表面将形成衰减的行波。弹性体平板超声行波驱动模型通过利用平板表面贴附的压电陶瓷产生逆压电效应激起衰减行波,从而驱动弹性体平板表面液滴沿行波方向移动。图 2所示为弹性体平板模型产生超声行波,a为位置间距。

|
| 图 2 弹性体平板模型产生超声行波 Fig. 2 Elastic planar model used to generate ultrasonic travelling wave |
两驻波方程分别为

|
(5) |

|
(6) |
式中:A为驻波振幅;ω为振动角频率;k为波数;φ为振动相位差。
分别将式(5) 和式(6) 展开,可以得到

|
(7) |
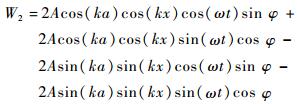
|
(8) |
通常两激励电压的相位差为90°,即有
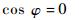
|
(9) |
则式(8) 化简为

|
(10) |
对比式(7),此时需令
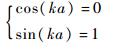
|
(11) |
由于k=2,则有

|
(12) |
即
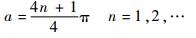
|
(13) |
因此,式(7) 最终化简为
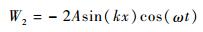
|
(14) |
则两驻波合成后能够产生单向行波
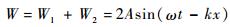
|
(15) |
需要多点激励产生行波时,只要两两之间满足在空间上和相位上相差90°即可。
2.2 弹性体平板驱动模型根据2.1节中的超声行波理论,提出如图 3所示的模型结构。该模型结构较为简单,在玻璃左端表面依次贴上4片压电陶瓷,极化方向均为z方向,压电陶瓷与玻璃的接触面统一为接地,其另一面分别接通正弦交流电为Usin(ωt)、Ucos(ωt)、-Usin(ωt)和-Ucos(ωt),U为驱动电压幅值,利用压电陶瓷的横向效应,形成时间上和空间上分别相差90°的驻波,因此在玻璃中形成超声行波,从而驱动液滴移动。

|
| 图 3 产生超声行波的结构简图 Fig. 3 Structure diagram of generating ultrasonic travelling wave |
建立数学模型时假设:① 液滴流动为层流不可压缩;② 假定液滴移动过程中液滴与壁面的接触角为静态接触角,忽略液滴运动时动态接触角受接触线移动速度以及壁面粗糙度的影响; ③ 液滴的半径为2mm,小于毛细长度lc=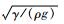
液滴为椭球形,其长半轴R和短半轴h分别为2.0和1.8mm。几何模型的结构参数见表 1。
| 类型 | 长度/mm | 厚度/mm |
| 玻璃平板 | 150 | 3 |
| 压电陶瓷 | 5π/4 | 1 |
3.2 边界条件
物理场接口选择层流两相流-移动网格和压电设备。多物理场耦合固体力学、静电和层流两相流,压电效应耦合固体力学和静电。
3.2.1 固体力学对固体力学,线弹性材料设置为几乎不可压缩材料。通常在3D笛卡儿坐标系中,压电陶瓷的材料参数为沿z方向极化,因此需旋转压电陶瓷的极化方向对准默认坐标系y方向。选择材料的方向为xz平面,旋转材料使它的z方向与默认坐标系的y方向重合,材料的x方向与默认坐标系的x方向重合。在本文研究中,将默认坐标系设置为x-z坐标系。对于平板玻璃,左端为固定约束,右端为自由边界条件。
3.2.2 层流两相流对层流两相流-移动网格,设置液滴与玻璃表面的接触角θ为π/2。
液滴流经玻璃表面会受到表面的影响,通常边界处的流动速度会逐渐趋于壁面的速度。由于玻璃表面静止,通常情况下液滴在壁面处的移动速度为零。经过管道流的实验发现,有时管道流量的实验测量值会大于理论值,尤其当管道壁面由疏水材料制作,实验流量会显著增加。Navier在1823年提出了线性滑移边界条件,靠近固体表面存在一个滑移速度uslip[23]。为了消除z=0时,存在剪切应力趋向于无穷大而引起润湿接触线处的应力奇异性[24]的情况,更加真实反映液滴在固-液接触界面上的速度,采用Navier线性滑移边界条件:
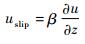
|
(16) |
在z=0处设置Navier滑移长度β= 0.2Δh,边界条件选择为静态壁,其中Δh为局部的网格单元尺寸。
预置网格位移,选择dz=0,即
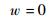
|
(17) |
对外部流体界面,设置表面张力γ为0.07N/m。全局坐标系下,在t=0s时,V=(u, w)=(0, 0)μm/s,其中u和w分别为沿x和z方向的速度。
3.3 材料参数锆钛酸铅(PZT)属于人工材料,需经过极化过程才能表现出压电特性。压电陶瓷的材料选择PZT-4,弹性体平板的材料选择Glass (quartz),液滴的材料选择Water, liquid。25 ℃下液滴的动力黏度为0.893×10-3 Pa·s,密度为1000kg/m3。压电陶瓷PZT-4的密度为7500kg/m3,玻璃的材料参数见表 2。
| 参数 | 弹性模量/Pa | 密度/(kg·m-3) | 泊松比 |
| 数值 | 7×1010 | 2 210 | 0.24 |
压电陶瓷PZT-4的压电矩阵为

|
相对介电常数矩阵为

|
弹性矩阵为

|
为了保证数值仿真的精度,这就要求在划分网格时尽量增加网格数来减小网格尺寸,但是这将增加了计算机内存的开销,数值仿真时间会大大增加,因此,为了平衡仿真精度与模拟时间,使用物理场控制的自适应网格划分,选择网格类型为粗化。本文的最大驱动频率为3MHz,在用户控制网格中可以看到对液滴校准的网格划分类型为流体动力学,最大单元尺寸为0.624mm,最小单元尺寸为0.024mm,满足模拟精度要求。
4 行波分析驱动频率为压电陶瓷一阶谐振频率且f=2.2121×105Hz,此时可以计算得到振动周期T≈0.00452ms,驱动电压为40V,30ms以后取20个周期对模型进行瞬态分析,数值模拟时间设置为:range(0, 0.01, 30),range(30, 4.52×10-4, 30.0904),单位为ms。记录弹性体平板玻璃质点x=20mm,z=2mm处的1个周期内质点运动轨迹,如图 4所示。表 3为对应为图 4中所观测质点x和z方向位移与时间的关系,可以知道运动轨迹相对坐标原点来说是顺时针方向。由于仿真时给定的周期不是精确值,并且由于存在端反射问题,引起机械波振幅会出现叠加,其幅值存在细微变化,因此所观测质点的轨迹不是闭合的椭圆运动轨迹,可以看到,椭圆轨迹较为规整,这与文献[3]中圆环超声行波微泵模型的行波运动分析结果相一致。

|
| 图 4 质点的椭圆运动轨迹 Fig. 4 Elliptical motion trail of particle |
| 时间/ms | x方向位移/nm | z方向位移/nm |
| 30.085880 | 3.654254 | 35.945566 |
| 30.086332 | 37.307580 | 42.905864 |
| 30.086784 | 56.858371 | 35.665642 |
| 30.087236 | 55.340976 | 17.141958 |
| 30.087688 | 33.690540 | -5.537054 |
| 30.088140 | 0.086644 | -24.081458 |
| 30.088592 | -33.196754 | -32.023728 |
| 30.089044 | -54.042325 | -26.239285 |
| 30.089496 | -54.650676 | -7.623552 |
| 30.089948 | -34.476498 | 18.330271 |
| 30.090400 | -0.687655 | 42.223590 |
对弹性体平板玻璃x方向为20~60mm区间,z方向恒定为2mm,观察在此截面上行波的瞬时状态,如图 5所示。可以看到随着时间推移,该波形沿着x轴的正方向移动,表明液滴的运动方向也将是沿着x轴的正方向运动,验证了驱动液滴的可行性。

|
| 图 5 行波瞬时状态 Fig. 5 Transient state of travelling wave |
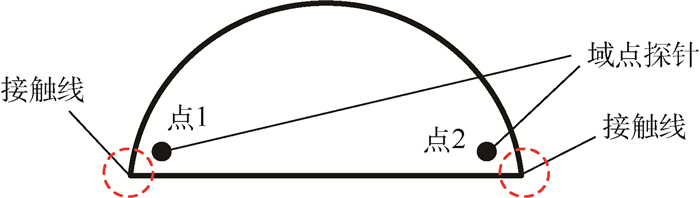
本文中忽略了液滴重力的影响,考虑表面张力与滑移边界条件影响下液滴的运动,激励频率为压电陶瓷一阶固有频率,所施加交流电的电压幅值为40V,仿真时间为60ms,时间步长为0.01ms。在靠近液滴接触线的内部两点添加域点探针,两域点探针对称分布,见图 6,分别记录两域点探针沿x方向的速度变化,如图 7所示。可以看到,液滴在超声行波的驱动下进行收缩-铺展的正弦振荡运动,由图 7可以知道振动周期约为26ms,可计算得到液滴的振动圆频率约为38.5Hz,与激励频率并不一致。因为对压电陶瓷施加的交流电的频率达到数万赫兹时,液滴不能及时地响应高频信号的激励。采用不同的超声行波激励频率以及驱动电压分别进行仿真分析,测得的液滴振动周期仍然约为26ms。Lamb[25]忽略液滴的黏性阻尼,提出了自由液滴的不同共振模态下的频率表达式,再结合所研究的液滴为椭圆,于是可以将方程写为
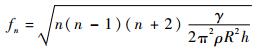
|
(18) |
|
| 图 6 添加域点探针 Fig. 6 Adding domain point probe |

|
| 图 7 液滴内部两点沿x方向的速度 Fig. 7 Velocity of two points inside droplet along x direction |
式中:R为椭圆的长半轴;h为椭圆的短半轴;n为模态阶数,n≥2。
此时,R=2×10-3m和h=1.8×10-3m代入式(18) 计算可得,当n=2时,则有f2=62.8Hz,对应为第2阶共振模态。因此,液滴在高频信号的激励下,推断液滴由于超声行波的驱动,受到表面张力、接触线滞后和基底驱动力等的相互耦合作用,以其第1阶低频摇摆模态进行着收缩-铺展的运动。
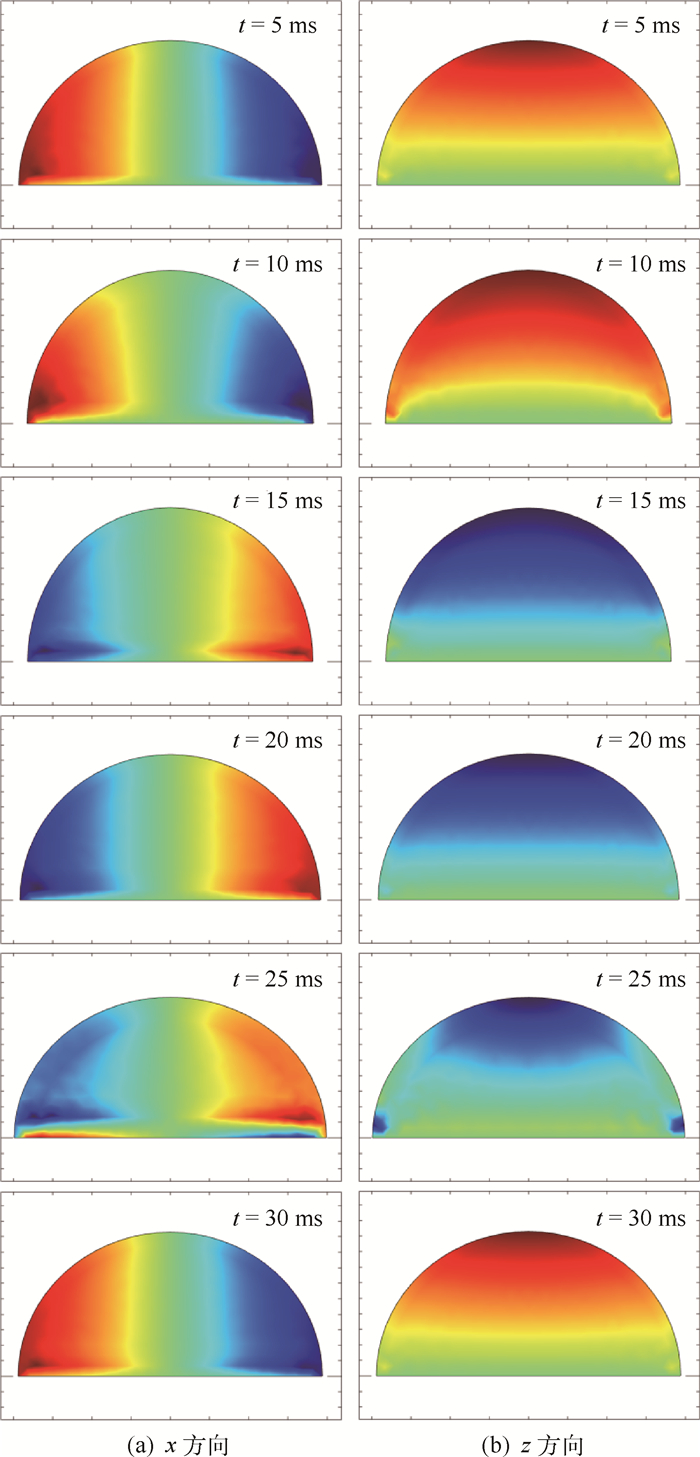
图 8所示为液滴在不同时刻下分别沿x方向和z方向的运动状态,红色代表速度为正值,蓝色代表速度为负值。① t=5ms时,液滴处于收缩阶段。对x方向而言,液滴中间部分的速度几乎为零;对z方向而言,液滴与基底接触的速度几乎为零。② t=10ms时,液滴此时仍然处于收缩的运动状态,但收缩的程度减小,可以看到z方向上液滴左、右两侧接触线处有明显的沿z轴的速度。可见,接触线是否发生移动对液滴的响应起着重要作用。③ t=15ms时,液滴已经处于铺展状态,在z方向上液滴整体速度沿z轴负方向,并且速度逐渐减小;与基底接触的速度几乎为零,但是液滴的两侧接触线处有明显的沿z轴负方向的速度。④ t=20ms时,液滴仍处于铺展状态。⑤ t=25ms时,可以看到,液滴半径铺展到最大后开始收缩。有一个特别的现象是,在x方向上,与基底接触面处的速度首先发生变化。可见,液滴内部速度场的变化对接触线是否发生移动有着重要作用。在接触线处沿z轴负方向存在有速度量,而与基底接触的速度几乎为零。⑥ t=30ms时,液滴处于类似于t=5ms时的运动状态。综合以上沿z方向的速度分析,可以得出液滴与基底接触的速度几乎为零,但是接触线处有明显不为零的速度量,可以推断接触线是否发生移动与速度的变化密切相关。
|
| 图 8 不同时刻下的液滴运动状态 Fig. 8 Droplet motion state at different moments |
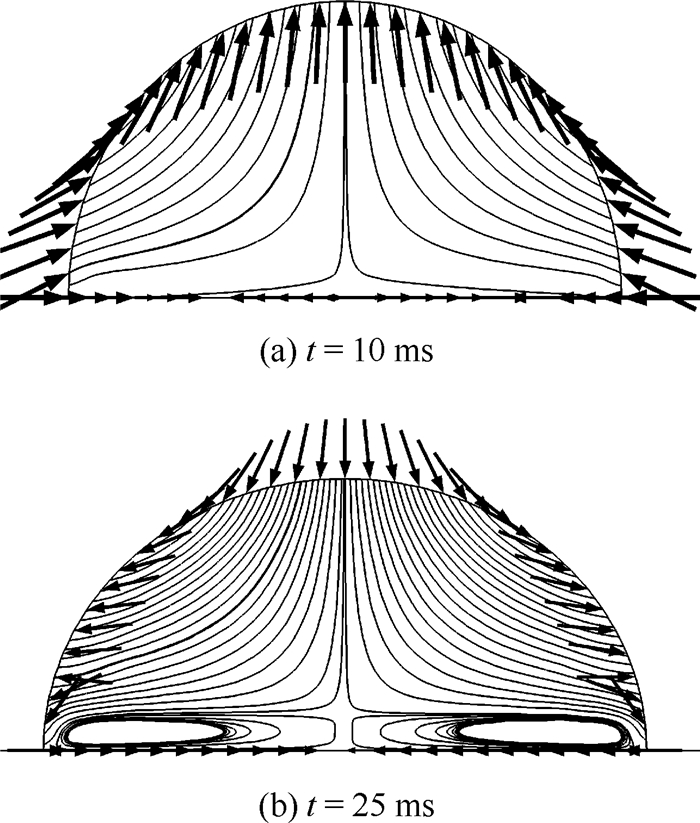
考虑到图 8中接触线处有明显的沿z轴的速度的情况,图 9为t=10ms和t=25ms时液滴的流场。t =10ms时,液滴仍处于收缩状态,但是与基底接触的速度开始发生变化,呈现速度对抗,表明液滴有铺展的趋势。在忽略重力影响的情况下,推断液滴内部速度场的变化为基底驱动力、表面张力和黏性滞后等作用的耦合结果。t=25ms时,由于远离基底的速度在表面张力的作用下还未完全减小至零,此时在基底驱动力的作用下与基底接触的速度已经发生180°的改变,从而导致了液滴两侧出现漩涡。
|
| 图 9 不同时刻下液滴的流场 Fig. 9 Flow field of droplet at different moments |
为研究液滴内部流场的分布,其驱动频率f=2.2121×105Hz,驱动电压幅值U=40V,仿真时间为10s,时间步长为0.01s,网格划分为更加细化。图 10所示为在t=5s时液滴的流场图,液滴移动方向为x正方向,分析发现t=2s和t=10s时的结果是类似的。对液滴速度矢量分析,可以看到液滴左侧内部出现一个漩涡,这与文献[13]使用格子Boltzmann方法研究润湿性梯度驱动液滴运动时液滴内部速度矢量是一致的。从漩涡分析发现漩涡两侧的接触角存在显著差异,文献[26]中提到,只要液滴两侧接触角的最大差值大于接触滞后的阈值,液滴将发生移动。漩涡中心为近似为一椭圆,其长轴与x轴的夹角大约为45°,越往外的椭圆(非规则椭圆)的长轴与x轴的夹角逐渐减小。可以认为,在惯性作用下沿着基底方向上液滴运动的对称性被打破,因此引起液滴的纯粹受迫运动。综合图 8的分析,可以得出液滴运动不是单纯由于收缩-铺展而引起的平动,而是类似于棘轮效应的运动,液滴滚动着朝前运动。

|
| 图 10 液滴流线图(t=5s) Fig. 10 Streamline of droplet (t=5s) |
在压电陶瓷上分别施加交流电的激励频率为1.6×105、2.212 1×105和1×106Hz, 液滴动力黏度为0.893×10-3Pa·s,驱动电压为40~100V,电压间隔为5V,液滴移动速度与驱动电压之间的关系如图 11所示。对PZT压电陶瓷来说,振动位移与驱动电压近似为线性关系。可见,液滴移动速度总体上随驱动电压的增加而增大。液滴移动速度随驱动电压呈现波动性增加,由于振动位移增加非常小,因此速度的增幅也非常微小。

|
| 图 11 液滴移动速度随驱动电压的变化 Fig. 11 Variation of droplet moving velocity with driving voltage |
25 ℃下液滴的动力粘度为0.893×10-3Pa·s,在压电陶瓷上所施加的驱动电压为40V,驱动频率为1~3MHz,频率间隔为0.1MHz,液滴移动速度与驱动频率之间的关系如图 12所示。

|
| 图 12 液滴移动速度随驱动频率的变化 Fig. 12 Variation of droplet moving velocity with driving frequency |
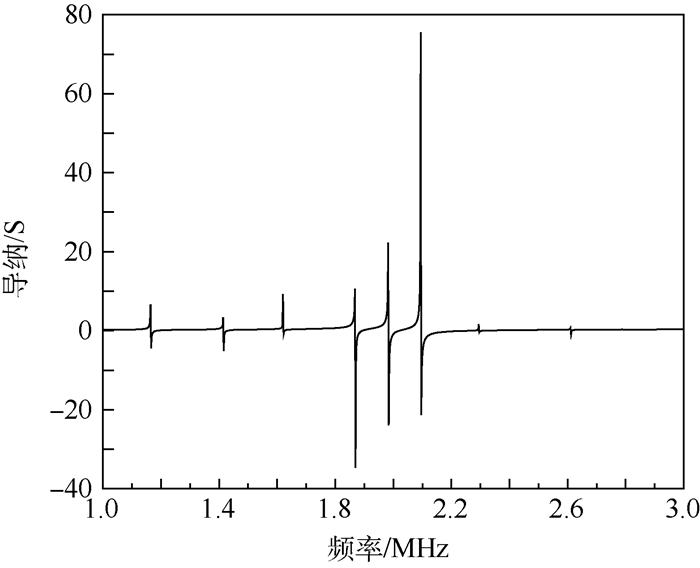
利用COMSOL多物理场仿真软件进行频率扫描的频域分析,在后处理结果中建立一维绘图组,使用全局绘图,可得到压电振子任意一点的导纳频率响应曲线,如图 13所示。由图可见,压电振子导纳图在谐振频率附近都出现了一个峰值点和谷值点,电压相位在峰值点和谷值点之间发生突变。这是由于将交流电压施加于压电振子上,压电振子产生机械变形,同时由于机械变形导致正压电效应产生了一定的电压,对所施加的交流电压进行反馈。当外加交流电压的频率与压电振子的机械谐振频率接近时,压电振子的机械振动幅度将变得更大,驱动电压与反馈电压同相相加,流过压电振子的电流最大,此时对应压电振子的导纳最大,即阻抗最小。当继续增加驱动电压的频率并超过谐振点,反馈电压逐渐滞后驱动电压,并在某个频率处与驱动电压反相,使流过压电振子的电流最小,压电振子呈现出导纳最小,即阻抗最大。
|
| 图 13 压电振子的阻抗频率响应曲线 Fig. 13 Impedance frequency response curve of piezoelectric vibrator |
由于液滴是以第1阶低频摇摆模态运动的,从图 12中可以看到,驱动频率的变化对液滴移动速度的影响并不大,但是随驱动频率的增加,液滴速度呈现出与压电振子输入导纳响应曲线的相同特性,液滴移动速度在9.5~10.0mm/s之间波动。
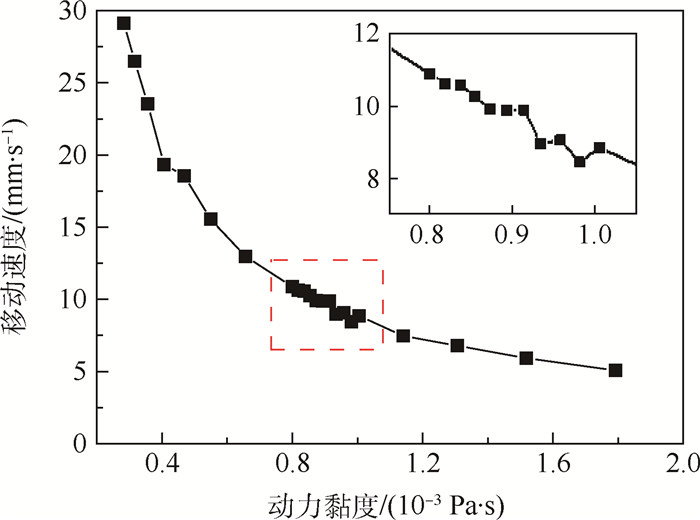
5.3 液滴移动速度与动力黏度的关系在压电陶瓷上施加交流电的驱动频率为2.2121×105Hz,驱动电压为40V,液滴移动速度与液滴动力黏度之间的关系见图 14。可见,液滴移动速度在整体趋势上随动力黏度的增加而减小,液滴移动速度与动力黏度成反比例函数关系。在动力黏度为0.800×10-3~1.005×10-3Pa·s之间进行了较为细致地研究,此时对应的温度为20~30℃,发现液滴移动速度变化的差值不大,随动力黏度的增加而波动性减小。动力黏度为0.283×10-3Pa·s时,液滴移动速度为29.125mm/s;动力黏度为1.792×10-3Pa·s时,液滴移动速度为5.0734mm/s。因此,动力黏度对液滴移动速度的影响非常明显。经过曲线拟合,得到液滴移动速度与动力黏度的表达式为
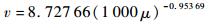
|
(19) |
|
| 图 14 液滴移动速度随动力黏度的变化 Fig. 14 Variation of moving velocity of droplet with dynamic viscosity |
图 15(a)所示为分区压电陶瓷,图 15(b)所示为疏水玻璃表面,利用压电陶瓷产生超声行波驱动液滴运动的实验结果。实验样品压电陶瓷贴于玻璃一侧,贴有压电陶瓷的一侧朝下放置。实验工况为25 ℃、液滴动力黏度为0.893×10-3Pa·s,液滴静态接触角为90°,驱动电压为100V,驱动频率为900kHz。在t1时刻下液滴静止于玻璃表面,t2时刻液滴停止运动,在t1~t2阶段液滴处于运动状态,且移动速度约为9mm/s。本文所设计的弹性体平板驱动模型的液滴移动速度能够与图 15的实验结果较好地吻合。

|
| 图 15 液滴运动实验结果 Fig. 15 Experimental results of droplet motion |
本文基于超声行波理论提出了一种弹性体平板驱动模型,研究了疏水表面液滴的运动特性,主要得出以下结论:
1) 随着时间推移,弹性体平板超声行波驱动模型所产生的行波沿着x轴的正方向移动,表明液滴的运动方向也将是沿着x轴的正方向运动,验证了驱动液滴的可行性。
2) 液滴在超声行波的驱动下进行收缩-铺展的正弦振荡运动。液滴在高频信号的激励下,推断液滴由于超声行波的驱动,受到表面张力、接触线滞后和基底驱动力等的相互耦合作用,以其第1阶低频摇摆模态进行着收缩-铺展的运动。
3) 通过流场分析发现,当液滴半径铺展到最大后开始收缩时,液滴与基底接触面处的速度首先发生变化,表明液滴内部速度场的变化对接触线是否发生移动有着重要作用。液滴内部流场存在一个类似于椭圆形的漩涡,说明液滴运动不是单纯由于收缩-铺展而引起的平动,而是滚动着朝前运动。
4) 探讨了液滴移动速度与驱动电压、驱动频率以及动力黏度的关系,结果表明液滴移动速度受动力黏度影响较为显著,受驱动电压和驱动频率的影响甚小。这为实际应用中的分区或分片压电陶瓷的生产制作以及在弹性体平板表面驱动液滴运动提供了一定的理论基础和依据。
| [1] | BECKER J, GRUN G. The thin-film equation:Recent advances and some new perspectives[J]. Journal of Physics Condensed Matter, 2005, 17 (9): S291–S307. DOI:10.1088/0953-8984/17/9/002 |
| [2] | SINGHAL V, GARIMELLA S V, RAMAN A. Microscale pumping technologies for microchannel cooling systems[J]. Applied Mechanics Reviews, 2004, 57 (3): 191. DOI:10.1115/1.1695401 |
| [3] |
魏长智, 魏守水, 张冲. 超声行波微流体驱动的流动特性分析[J].
应用基础与工程科学学报, 2013, 21 (1): 97–106.
WEI C Z, WEI S S, ZHANG C. Flow characteristics analysis of ultrasonic traveling wave micro-fluid driving[J]. Journal of Basic Science and Engineering, 2013, 21 (1): 97–106. (in Chinese) |
| [4] | SHI W, QIN J, YE N, et al. Droplet-based microfluidic system for individual Caenorhabditis elegans assay[J]. Lab on a Chip, 2008, 8 (9): 1432–1435. DOI:10.1039/b808753a |
| [5] | ABDELGAWAD M, WATSON M W, WHEELER A R. Hybrid microfluidics:A digital-to-channel interface for in-line sample processing and chemical separations[J]. Lab on a Chip, 2009, 9 (8): 1046–1051. DOI:10.1039/b820682a |
| [6] | YOUNG T. An essay on the cohesion of fluids[J]. Philosophical Transactions of the Royal Society of London, 1805, 95 : 65–87. DOI:10.1098/rstl.1805.0005 |
| [7] | WENZEL R N. Resistance of solid surface to wetting by water[J]. Industrial & Engineering Chemistry, 1936, 28 (8): 988–994. |
| [8] | CASSIE A B D, BAXTER S. Wettability of porous surfaces[J]. Transactions of Faraday Society, 1944, 40 : 546–551. DOI:10.1039/tf9444000546 |
| [9] | CHAUDHURY M K, WHITESIDES G M. How to make water run uphill[J]. Science, 1992, 256 (5063): 1939–1541. |
| [10] | DANIEL S, CHAUDHURY M K. Rectified motion of liquid drops on gradient surfaces induced by vibration[J]. Langmuir, 2002, 18 (9): 3404–3407. DOI:10.1021/la025505c |
| [11] | DANIEL S, SIRCAR S, GLIEM J, et al. Ratcheting motion of liquid drops on gradient surfaces[J]. Langmuir, 2004, 20 (10): 4085–4092. DOI:10.1021/la036221a |
| [12] |
王晓东, 彭晓峰, 陆建峰, 等. 粗糙表面接触角滞后现象分析[J].
热科学与技术, 2003, 2 (3): 230–234.
WANG X D, PENG X F, LU J F, et al. Analysis of contact angle hysteresis on rough surfaces[J]. Journal of Thermal Science and Technology, 2003, 2 (3): 230–234. (in Chinese) |
| [13] |
石自媛, 胡国辉, 周哲玮. 润湿性梯度驱动液滴运动的格子Bolzmann模拟[J].
物理学报, 2010, 59 (4): 2595–2600.
SHI Z Y, HU G H, ZHOU Z W. Lattice Boltzmann simulation of droplet motion driven by gradient of wettability[J]. Acta Physica Sinica, 2010, 59 (4): 2595–2600. DOI:10.7498/aps.59.2595 (in Chinese) |
| [14] | DAS A K, DAS P K. Multimode dynamics of a liquid drop over an inclined surface with a wettability gradient[J]. Langmuir, 2010, 26 (12): 9547–9555. DOI:10.1021/la100145e |
| [15] |
周建臣, 耿兴国, 林可君, 等. 微液滴在超疏水表面的受迫振动及其接触线的固着-移动转变[J].
物理学报, 2014, 63 (21): 216801.
ZHOU J C, GENG X G, LIN K J, et al. Stick-slip transition of a water droplet vibrated on a superhydrophobic surface[J]. Acta Physica Sinica, 2014, 63 (21): 216801. DOI:10.7498/aps.63.216801 (in Chinese) |
| [16] | WALKER S W, SHAPIRO B. A control method for steering individual particles inside liquid droplets actuated by electrowetting[J]. Lab on a Chip, 2005, 5 (12): 1404–1407. DOI:10.1039/b513373b |
| [17] | WALKER S W, SHAPIRO B. Modeling the fluid dynamics of electrowetting on dielectric (EWOD)[J]. Journal of Microelectro-mechanical Systems, 2006, 15 (4): 986–1000. DOI:10.1109/JMEMS.2006.878876 |
| [18] | WALKER S W, SHAPIRO B, NOCHETTO R H. Electrowetting with contact line pinning:Computational modeling and comparisons with experiments[J]. Physics of Fluids, 2009, 21 (10): 443–451. |
| [19] | LI F, MUGELE F. How to make sticky surface slippery:Contact angle hysteresis in electrowetting with alternating voltage[J]. Applied Physics Letters, 2008, 92 (24): 244108. DOI:10.1063/1.2945803 |
| [20] | GAO Y, LI Y G, ZHANG J F. Two-dimensional actuation of liquid using surface acoustic wave[J]. Optics and Precision Engineering, 2009, 17 (7): 1548–1552. |
| [21] | BATCHELOR G K. An introduction to fluid dynamics[M]. Cambridge: Cambridge University Press, 2000: 73-79. |
| [22] | BAL G, BEKIROGLU E. Servo speed control of travelling-wave ultrasonic motor using digital signal processor[J]. Sensors and Actuators A:Physical, 2004, 109 (3): 212–219. DOI:10.1016/j.sna.2003.10.019 |
| [23] | NETO C, EVANS D R, BONACCURSO E, et al. Boundary slip in Newtonian liquids:A review of experimental studies[J]. Reports on Progress in Physics, 2005, 68 (12): 2859–2897. DOI:10.1088/0034-4885/68/12/R05 |
| [24] | BLAKE T D, HAYNES J M. Kinetics of liquid/liquid displacement[J]. Journal of Colloid and Interface Science, 1969, 30 (3): 421–423. DOI:10.1016/0021-9797(69)90411-1 |
| [25] | LAMB H. Hydrodynamics[J]. Hydrodynamics New York Dover, 1932, 6 (4): 181–185. |
| [26] | DONG L, CHAUDHURY A, CHAUDHURY M K. Lateral vibration of water drop and its motion on a vibrating surface[J]. European Physical Journal E, 2006, 21 (3): 231–242. DOI:10.1140/epje/i2006-10063-7 |



